1 Introduction

Currently, novel high-temperature alloys based on refractory metals[1,2] have attracted attention in the development of alloys beyond the Ni-based superalloys.[3,4,5,6] Chromium (Cr) can be used as high-temperature material because it has a higher melting point and lower density than Ni. Cr-based alloys strengthened by the Laves phases, such as Cr-Nb[7,8,9,10] and Cr-Ta[11,12] alloys, exhibit excellent high-temperature strength. However, further improvement of their oxidation resistance and low-temperature brittleness is required. Si addition enhances both the nitridation and oxidation resistance of chromium, and the Cr-Si alloys show an excellent oxidation resistance.[13,14] Recently, we found that the Cr-Si binary alloys have higher specific strength and oxidation resistance at high temperatures than those of Ni-based superalloy Mar-M247.[15] In addition, the CrSi2 phase has been investigated as thermoelectric material.[16,17,18] An accurate phase diagram of the Cr-Si system can guide alloy design and heat treatment to enhance the properties of the Cr-Si alloys. However, for the phase diagrams including Cr, reliable experimental data are limited due to the difficulty of conducting the experiments at high temperatures. In this study, the melting point of pure Cr and phase equilibria in the Cr-Si binary system were experimentally investigated.

2 Literature Information

2.1 Melting Point of Pure Cr

The reported melting points are between 1842 and 1933 °C, which can be divided into three classes: ~1930, ~1895, and ~1850 °C. The melting points reported for pure Cr are summarized in Table 1. The recommended melting point is different among compilations,[21,22,23] and its true value is still under discussion.

Table 1 Summary of experimental studies and recommended melting points for pure Cr
Full size table

The melting point, 1907 ± 20 °C, in the SGTE (Scientific Group Thermodata Europe)[19] database is based on the assessment by Andersson,[20] who adopted the value in a compilation published by Gurvich et al.[21] Gurvich et al. chose the melting points of pure Cr reported by Grube and Knabe[24] (1890 ± 10 °C), Putman et al.[26] (1892 °C), Bloom et al.[30] (1903 ± 10 °C), Pan[32] (1893 ± 10 °C), and Nedumov and Grigorovich33 (1933 °C) as reliable data among the experimental information[24,25,26,27,28,29,30,31,32,33] reported at that time, which lies in the highest and second-highest classes. Bloom et al.[30] measured the melting point as 1903 ± 10 °C by thermal analysis using a tungsten-molybdenum thermocouple and high purity samples having about 0.008% O, 0.002% N, and negligible carbon. In addition, Putman et al.[26] investigated the melting point of Cr using a sample containing approximately 0.5% O using the same method.

However, Hultgren et al.[22] suggested 1857 ± 20 °C based on the values by Carlile et al.[25] (1860 ± 20 °C), Greenaway et al.[28] (1845 ± 10 °C), and Haworth and Hume-Rothery[31] (1849 ± 20 °C), which Gurvich et al. did not adopt. Carlile et al.[25] measured the solidification temperature of pure Cr using an optical pyrometer calibrated using the melting point of pure Ni, and 1860 ± 20 °C was obtained after extrapolation to zero impurity content. Greenaway et al.[28] conducted temperature measurement using a tungsten−molybdenum thermocouple and used an optical pyrometer for temperature calibration, from 1700 to 2200 °C. They also extrapolated to zero impurity content and estimated the melting point of pure Cr to be 1845 ± 10 °C. Haworth and Hume-Rothery[31] determined the melting point of pure Cr to be 1849 ± 20 °C based on heating measurements using an optical pyrometer. They confirmed the measurement accuracy using the melting point of pure metals (Mn, Ni, Pd, Pt, Rh, and Ir), i.e., within ± 10 °C in the range of 1300-1800 °C, within ± 15 °C in the range of 1800-2300 °C, and within ± 20 °C in the range 2300 °C-2700 °C.

Recently, experimental investigations report the melting point of pure Cr to be 1860 ± 6 °C determined by Rudy and Windisch[34] using the Pirani method[35,36] and 1842 ± 20 °C determined by Josell et al.[37] using the pulsed-heating technique. These values agree with the experimental data[25,28,31] accepted in Hultgren et al.'s compilation.[22] In addition, 1863 °C was recommended in the phase diagram compilation published by ASM International.[23]

2.2 Cr-Si Phase Diagram

Figure 1 shows the phase diagram of the Cr-Si binary system.[38] The crystal structures of the constituent phases[17,45,50,51,52,53,54] are in Table 2. The experimental data obtained by Chang[43] and Svechnikov et al.[44] have been used to evaluate the high Cr side. The solvus temperature of the Cr solid solution phase has been determined using metallography, X-ray diffraction (XRD), and differential thermal analysis (DTA). Transformation temperatures, including liquidus, solidus, and eutectic temperatures were determined using the Pirani method,[35,36] which is a technique to determine the melting point of an alloy by optical observation. However, the results obtained using the Pirani method can be inaccurate at high temperatures because of the difficulty in observing the liquid as it forms. Besides, Du and Schuster[40] have indicated that the transformation temperatures investigated by Chang[43] may be affected by carbon contamination because of the graphite die used during the fabrication of the alloys. Thus, these experimental results may be lower than the actual melting point of Cr-Si.

Fig. 1
figure 1

Phase diagram of the Cr-Si binary system assessed by Cui and Jung[38] using experimental data

Full size image
Table 2 Summary of crystal structure information in the Cr-Si system
Full size table

Pyatkova et al.[46] and Jurisch and Behr[45] have measured the homogeneity range of the Cr3Si phase at 1000 °C using the XRD and metallography. Regarding the Cr5Si3 phase, Chang[43] has suggested that structural transformation occurred between the α-Cr5Si3 and β-Cr5Si3 phases based on the results of DTA measurements. Du and Schuster.[40] applied the thermodynamic model of Ti5Si3 to describe the β-Cr5Si3. However, the crystal structure and solubility range of the Cr5Si3 phase have not been reported. In addition, the invariant reaction consisting of liquid, Cr3Si, and Cr5Si3 phases is under discussion. Recent thermodynamic evaluation by Chen et al.[39] has suggested that this reaction is peritectic; however, some evaluations have accepted eutectic reaction.[38,40,41]

The thermodynamic description of the phase diagram in the Cr-Si binary system has updated several times[38,39,40,41]; the latest one assessed by Cui and Jung[38] based on the experimental investigations[43,44,45,46,47,48,49] is shown in Fig. 1. This phase diagram consists of four intermetallic compounds, Cr3Si, Cr5Si3, CrSi, and CrSi2, in addition to the Cr and Si solid solutions.

3 Experimental Procedure

3.1 Alloy Preparation

Cr-Si alloys were made from high purity Cr (99.99%) and Si (99.999%). The impurity contents of Cr were measured using an inductively coupled plasma optical emission spectrometer (ICP-OES) to be 0.0147 mass% O, 0.0003 mass% N, 0.0022 mass% C, 0.0002 mass% S, less than 0.01 mass% P and Si, and less than 0.003 mass% Al, Cu, and Fe. Button ingots were prepared by arc melting in Ar gas atmosphere using a nonconsumable tungsten electrode on a copper hearth. The ingots were melted seven times to ensure chemical homogeneity. As-cast ingots were cut into pieces, and the surface was ground to remove the oxidized layer. The alloy composition is denoted as at% unless noted.

In this study, a pure W (99.9%) plate with a thickness of 0.5 mm was used as the reference sample for measuring specimen temperature using the pyrometer. Some disk samples were cut out of the W plate, and the surface of the disk was ground.

3.2 Heat Treatment

Each specimen for examining phase equilibria at temperatures between 1200 and 1400 °C was encapsulated in a quartz glass tube refilled with Ar gas. Then, it was heat-treated in electric resistance heating furnaces, followed by quenching in iced water. The Cr-Si alloys may react with the quartz glass tube (SiO2) because of the high oxygen affinity of Si. Therefore, during the heat treatment, Cr-Si alloys were separated from the quartz glass tube using tungsten wire twined around the sample.

The heat treatment for equilibration at 1500 and 1600 °C was conducted in a high-frequency induction heating furnace under a high purity Ar gas atmosphere. Figures 2(a) and (b) show the schematic and interior view of the furnace, respectively. The temperature was measured using a two-color pyrometer through the sapphire glass window, as shown in Fig. 2(c). In addition, we separated the Cr-Si specimen (3.5 × 5.5 × 1.5 mm) and tungsten reference sample (3.2 φ × 0.5 mm) using a thin Al2O3 powder layer (about 1-mm thickness), laid on the top of a tungsten plate (17.0 φ × 0.5 mm), and this setup was placed in a tungsten crucible, as illustrated in Fig. 2(d). The tungsten plate and Al2O3 powder were used to avoid crucible contaminations and heat treatment reactions, respectively. It was difficult to obtain an accurate temperature of the Cr-Si alloys because of surface changes during the heat treatment due to evaporation of Cr. Therefore, we measured the temperature of the nearby tungsten reference sample instead. The error in this method was estimated by measuring the melting points of Ni (99.9%, Tm = 1455.0 °C), Pd (99.9%, Tm = 1554.8 °C), and Pt (99.9%, Tm = 1768.3 °C). Each pure metal was heated using a tungsten reference sample at about 10 °C/min in the furnace, and the temperatures of both pure metal and tungsten reference samples were monitored. The temperatures of the tungsten reference samples were recorded when the melting temperatures of the pure metals were detected from the temperature-time curves; they are plotted against the accepted melting temperatures of pure metals in Fig. 3. The results indicate that the temperature accuracy is within ± 20 °C, which can be used as a thermometer in heat treatments conducted at high temperatures. The specimens heat-treated at 1500 and 1600 °C were furnace-cooled after switching off the high-frequency induction current, where the cooling rate was about 25 °C/s at high temperatures, between 1600 and 1200 °C.

Fig. 2
figure 2

(a) Schematic of a high-temperature furnace, (b) interior view of high-temperature furnace, (c) view during heat treatment using two-color pyrometer, and (d) schematic illustration around specimen designed in this work

Full size image
Fig. 3
figure 3

Relation between measured and reported melting temperatures for estimation of temperature error in the present experiments

Full size image

3.3 Measurements of Equilibrium Compositions

The chemical compositions of the equilibrium phases were measured using a field-emission electron probe microanalyzer (FE-EPMA: JEOL JXA-8500F) equipped with a wavelength-dispersive-x-ray spectroscopy (WDS), with a 20-kV accelerating voltage and 10-nA beam current. The concentrations were measured from ten points per phase and averaged without the maximum and minimum values. In addition, line analysis across an interphase boundary was conducted to confirm the absence of a composition gradient to ensure the equilibrium state.

3.4 Determination of Transformation Temperatures

Phase transformation temperatures in the Si-rich portion were determined using a differential scanning calorimeter (DSC: Netzsch DSC-404C). The DSC measurement was performed using an Al2O3 pan capped with an Al2O3 lid at a heating and cooling rate of 10 °C/min in Ar gas flow, and the temperature calibration using high purity Sn (99.99%, Tm = 231.9 °C), Al (99.99%, Tm = 660.1 °C), Ag (99.99%, Tm = 951.5 °C), Au (99.9%, Tm = 1063.0 °C), and Ni (99.99%, Tm = 1455.0 °C) was applied. The oxygen trap system (Netzsch OTS®) was employed to reduce the harmful effect of residual oxygen.

However, phase transformation temperatures in the Cr-rich portion, where the temperature is high, were investigated using a differential thermal analyzer (DTA: Netzsch STA 449 F3 Jupiter). The DTA measurement was performed in a static atmosphere of high purity He to prevent the evaporation of Cr. Each sample was placed on Al2O3 powder in a tungsten crucible with a tungsten lid. The effect of heating and cooling rates were examined at 2, 5, and 10 °C/min for pure Cr, whereas all other samples were measured at a heating and cooling rate of 10 °C/min. The calibration at different rates were conducted using high purity Ni (99.9%, Tm = 1455.0 °C), Pd (99.9%, Tm = 1554.8 °C), and Pt (99.9%, Tm = 1768.3 °C).

4 Result and Discussion

4.1 Melting Point of Pure Cr

Figure 4(a) shows the DTA profiles of pure Cr obtained through measurements at heating rates of 2, 5, and 10 °C/min. The melting points, defined as the onset of the peaks, were close for all heating rates, suggesting that the dependence on the heating rate is negligible. In addition, the DTA heating and cooling measurement at a rate of 10 °C/min were repeated twice; the heating curves are shown in Fig. 4(b). The melting point in the first and second heating cycles were 1859.2 and 1856.6 °C, respectively. This decrease in melting point is due to increased impurity during the measurement. The ICP-OES revealed that the sum of O and N contents in Cr, before and after the DTA measurement, including melting is 0.0274 mass% (0.0196 mass% O and 0.0078 mass% N), and 0.0610 mass% (0.0509 mass% O and 0.0101 mass% N), respectively. The melting points obtained by Carlile et al.[25] and Greenaway et al.,[28] as well as this study, are plotted against the impurity (O + N) contents in Fig. 5. The slope of the three sets of data is similar. The results in this study are close to the line by Carlile et al.,[25] and the melting point of pure Cr is extrapolated to be 1861 °C. Moreover, the DTA measurements were conducted six times, and the uncertainties associated with the measurements were within ± 3 °C. Therefore, we concluded that the melting point of Cr is 1861 ± 3 °C, which is close to the values reported by Rudy and Windisch (1860 ± 4 °C).34

Fig. 4
figure 4

(a) DTA heating curves measured for pure Cr with a heating rate of 2, 5, and 10 °C/min, and (b) heating rate of 10 °C/min for two-cycle under He atmosphere

Full size image
Fig. 5
figure 5

Correlation between the melting point of pure Cr and impurity (O and N) contents measured using ICP-OES

Full size image

Previous reports and this work focused on liquidus and solidus in the Cr-rich portion of the Cr-Si system are plotted in Fig. 6. As shown in this figure, the melting point of pure Cr accepted in SGTE (1907 °C)[19] is consistent with the liquidus and solidus temperature of the Cr solid solution phase by Svechnikov et al.[44] However, it is about 50 °C higher than the values measured by Rudy and Windisch,[34] Josell et al.,[37] and this study, and it is inconsistent with the liquidus and solidus investigated by Chang[43] and Svechnikov et al.,[44] as well as this study. A similar tendency has been observed in the Cr-Fe binary system. Xiong et al.[55] have pointed out that in the Cr-Fe system, there is a large discrepancy between the experimental solidus and liquidus lines and the melting temperature of pure Cr in the SGTE and that the temperature of SGTE may be too high. The melting point accepted in SGTE is based on the reported values.[24,26,30,32,33] However, it seems that aging of the thermocouples affected the temperature measurement,[27,29] and temperature calibration might be insufficient although much information is not written. Recently, the melting point of 1863°C has been recommended for pure Cr,[55,56] relying on the experimental data by Rudy and Windisch[34] and Josell et al.[37] and the phase diagram by ASM International.[23] The result of this study supports these recent recommendations but determined the melting point to be 1861 ± 3 °C through careful experiments.

Fig. 6
figure 6

Cr-rich portion of phase equilibria in high-temperature range of the Cr-Si system

Full size image

4.2 Thermal Analysis

The decrease in the melting point of pure Cr due to the contamination by O and N during the measurements was 2°C as shown in Fig. 5. This is considered to be the largest possible error in the Cr-Si system in the present work, because the highest reaction temperatures in Cr-Si alloys were lower than the melting point of pure Cr and Si is expected to make the samples more protective to oxygen and nitrogen. Therefore, the effect of O + N content on the phase diagram is negligible small in the Cr-Si binary system and the measured results are directly used in the binary system.

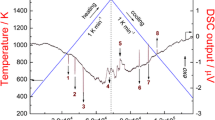
Experimental results of phase transformation temperatures determined using the heating curves of DTA and DSC (Figs. 7 and 8) and the chemical composition analyses using the FE-EPMA/WDS (Figs. 9-11) are summarized in Fig. 12. The phase diagram assessed by Cui and Jung[38] is superimposed with gray curves. Fig. 7 shows the DTA heating curves at a heating rate of 10 °C/min. In the Cr-7Si alloy shown in Fig. 7(a), a gradual fall and a tail can be recognized in the endothermic signal, corresponding to the solidus and liquidus temperatures, respectively. A sharp endothermic peak at around 1716 °C, followed by a small tail in Cr-14Si alloy shown in Fig. 7(b), is caused by the eutectic reaction of (Cr) + Cr3Si ↔ L. The solvus temperature of the Cr solid solution phase is determined by the tail of the endothermic peak at 1686 °C, as shown in the curve in Fig. 7(c). For the other alloys, the transformation temperatures are determined using the same method.

Fig. 7
figure 7

DTA heating curves measured for (a) Cr-7Si, (b) Cr-14Si, (c) Cr-20Si, (d) Cr-30Si, (e) Cr-35Si, (f) Cr-37Si, (g) Cr-39Si, (h) Cr-44Si, and (i) Cr-51Si alloys at a heating rate of 10 °C/min under He gas atmosphere

Full size image
Fig. 8
figure 8

DSC heating curves for (a) Cr-56Si, (b) Cr-65Si, (c) Cr-80Si, and (d) Cr-90Si alloys at a heating rate of 10 °C/min under an Ar gas atmosphere

Full size image
Fig. 9
figure 9

Back-scattered electron (BSE) images of as-cast microstructure of (a) Cr-33Si (b) Cr-35Si (at.%) alloys. “E” represents eutectic microstructure. (c) Phase diagram related to melting of Cr5Si3 phase in the Cr-Si system

Full size image

Figure 8 shows the DSC measurement results for alloys with high Si contents. The sharp endothermic signals are recognized in the curves, corresponding to the eutectic reaction and liquidus temperatures.

The transformation temperatures determined by DTA, and DSC measurements are in Table 3 and plotted in Fig. 12. The invariant temperatures coincide with the values obtained in the previous works (Table 4), except for the peritectic temperature consisting of liquid, Cr5Si3, and CrSi phase. The revised peritectic temperature (1442 °C) is about 20 °C higher than the previous values (1413 ± 5 °C[43] and 1425 ± 4 °C[40]), as shown in Table 4. The liquidus temperatures are also higher than the previous ones, as shown in Fig. 12. The congruent melting temperature of the CrSi2 phase is higher than the experimental value by Du and Schuster (1439 °C)[40]; however, it is in good agreement with that by Chang (1490 ± 20 °C).[43]

Table 3 Transformation temperatures determined by DTA and DSC analysis
Full size table
Table 4 Summary of invariant reaction temperatures determined by DTA and DSC measurements
Full size table

4.3 Reaction around Cr5Si3 Phase

There has been a discussion whether the invariant reaction related to the Cr5Si3 phase (the stoichiometric composition is Cr-37.5Si) is eutectic[38,40,41] or peritectic.[39,51] Figures 9(a) and (b) show as-cast microstructures of Cr-33Si and Cr-35Si alloys. Fine lamellar microstructure, with primary Cr3Si phase and fully lamellar microstructure, are observed in Cr-33Si and Cr-35Si alloys, respectively. Based on these microstructures, we concluded that the invariant reaction, involving the Cr3Si, Cr5Si3, and liquid phases, is eutectic, and eutectic composition is close to Cr-35Si. Moreover, the liquidus temperatures by DTA support this conclusion, as shown in Fig. 9(c). The liquidus temperatures for Cr-37Si alloy (1690.7 °C) and Cr-39Si alloy (1687.7 °C) are almost equal, indicating that the congruent temperature of Cr5Si3 is about 1690 °C as depicted in Fig. 9(c).

4.4 Equilibrium Composition of Two-Phase Alloys

Figures 10 and 11 show the two-phase microstructures for alloys heat-treated at 1300 to 1600 °C. The specimens show a two-phase structure that is coarsened to over 10 μm, which is sufficient for quantitative analysis using FE-EPMA/WDS. The equilibrium data are in Table 5 and plotted in Fig. 12 with previous key experimental data[40,42,43,44,45,46,47,48,49] and assessed phase diagram by Cui and Jung.[38] In this study, the phase boundaries determined using thermal analysis and FE-EPMA/WDS measurements correlate with the phase boundaries of Cr solid solution and Cr3Si phases.

Fig. 10
figure 10

Back-scattered electron (BSE) images of (a) Cr-12Si, (b) Cr-31Si and (c) Cr-44Si heat-treated at 1400 °C for 293 h and (d) Cr-61Si and (e) Cr-80Si heat-treated at 1300 °C for 336 h

Full size image
Fig. 11
figure 11

Back-scattered electron (BSE) images of (a) Cr-16Si heat-treated at 1600 °C for 3 h and (b) Cr-30Si heat-treated at 1500 °C for 15 h.

Full size image
Table 5 Equilibrium compositions of Cr-Si alloys measured by FE-EPMA
Full size table
Fig. 12
figure 12

Experimentally determined phase diagram of the Cr-Si system

Full size image

Compared to the reported phase equilibria, we found that the Cr solid-solution phase has lower solubility of Si than those reported in past studies[38,42,44] (Fig. 12). According to the phase diagram assessed by Cui and Jung,[38] the solubility range of the Cr3Si phase inclines toward the Si-rich side as temperature increases. The α-Cr5Si3 phase is treated as a line compound and the β-Cr5Si3 phase has a narrow solubility range because of insufficient experimental data. However, in that study, it was revealed that the Cr3Si single-phase region inclines toward the Cr-rich side as temperature increases, which agrees with the reports by Svechnikov et al.,[44] Jurisch and Behr,[45] and Pyatkova et al.,[46] however, stating that this phase has no solubility in the Si-rich side disagrees with Svechnikov et al.[44]. We found that the Cr5Si3 phase has a solubility range that extends toward the Si-rich side. These results suggest that the Cr3Si and Cr5Si3 phases are not so stable on the Si- and Cr-rich side from the stoichiometric compositions. The thermodynamic assessment is a scope of future studies. The existence of the homogeneity range of the CrSi2 phase has been suggested by Dudkin and Kuznetsova,[49] Dubrovskaya and Gel’d,[48] and Voronov et al.[47] using the electrical conductivity measurements. However, in this study, we found that the CrSi2 phase has almost no homogeneity range.

4.5 α-β Transformation of Cr5Si3 Phase

Chang[43] have claimed that there is a phase transformation in the Cr5Si3 phase at 1505 ± 20 °C through the DTA measurements, and later, high-temperature β-Cr5Si3 and low-temperature α-Cr5Si3 phases were adopted in the phase diagram of the Cr-Si system. However, the details of the phase transformation have not been investigated, and the crystal structure of the β-Cr5Si3 remains unknown. Figs. 13(a) and (b) show the XRD patterns of Cr-33Si alloy heat-treated at 1600 °C and 1300 °C for 4h and 7 days, respectively. These peaks are consistent with a mixture of Cr3Si and α-Cr5Si3, as shown in the lower part of Fig. 13. Moreover, no signal was detected by DTA and DSC measurements in Cr-35Si, as shown in Fig. 7(e). Therefore, we concluded that the α-β transformation of the Cr5Si3 phase does not occur and that only the α-Cr5Si3 exists as the Cr5Si3 intermetallic compound.

Fig. 13
figure 13

Powder XRD patterns of Cr-33Si heat-treated at (a) 1600 °C 4 h and (b) 1300 °C 7 days using Cu Kα radiation at room temperature. Calculated XRD patterns of (c) Cr3Si and (d) Cr5Si3

Full size image

5 Summary

In this study, the melting temperature of pure Cr and phase equilibria in the Cr-Si binary system were experimentally determined by thermal and equilibrium composition analyses. From the heating curves of the DTA measurements calibrated using pure metals, the melting point of pure Cr was determined to be 1861 ± 3 °C with the consideration of N and O impurities. This melting point is 46 °C lower than the one proposed by the SGTE unary database; however, it correlates, within the range of experimental error, with the latest experiments by Josell et al. and several previous studies. In the Cr-Si binary system, the thermal analysis revealed that the peritectic reaction temperature of liquid ↔ Cr5Si3 + CrSi and liquidus temperature in this concentration range are higher than the reported values. The congruent melting temperature of the CrSi2 phase was found to be higher. For the Cr5Si3 phase, the invariant reaction involving melting was confirmed to be a eutectic reaction of liquid ↔ Cr3Si + Cr5Si3, and the phase transformation, from the α-Cr5Si3 to β-Cr5Si3, that has been reported in previous phase diagrams was absent. Equilibrium compositions of two-phase alloys in the whole concentration range of the Cr-Si system were determined using FE-EPMA/WDS at temperatures between 1200 and 1600 °C. The solubility of Si in the Cr solid solution was determined. We found that the solubility range of the Cr3Si phase inclines toward the Cr-rich side, whereas the Cr5Si3 phase extended toward the Si-rich side. The CrSi2 phase was a line compound.