Introduction

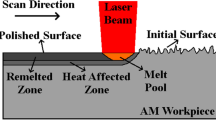
In directed energy deposition (DED) processes, a heat source is used to melt-deposited material as it is fed onto a substrate. The heat source is commonly a laser beam, an electron beam or an electric arc (Ref 1,2,3,4,5,6). The feedstock could be in the form of powder or wire (Ref 7). The laser powder-directed energy deposition (LP-DED) process combines a laser beam with powder material. Industrial interest in LP-DED is growing rapidly, especially because of its capability in repairing applications and in the production of large components (Ref 8,9,10). However, despite the enormous advantages that may be derived from the use of the LP-DED process, its applications is still limited (Ref 11). It has been observed in the literature that the surface quality and distortions are the most challenging issues in the LP-DED process (Ref 12,13,14). In fact, on average, the surface roughness obtained using the LP-DED process is three times higher than the surface roughness obtained with laser powder bed fusion processes (Ref 15, 16). Moreover, due to the higher heat input and uncontrolled substrate temperature, the residual stresses are also higher, and distortions of many centimeters may occur in large components (Ref 7). In both cases, the solutions used to overcome these problems are to consider an allowance on the surfaces and to introduce post-processing operations, such as heat treatments and machining operations (Ref 7). Process optimization, which can only be obtained as a result of a deep understanding of the effects of the process parameters on the characteristics of the final component, is fundamental to raise the production to an industrial level and to reduce the post-processing operation costs.

Smugeresky et al. (Ref 17) performed one of the first experimental investigations on the surface finishing of a 316L stainless steel thin wall produced by LP-DED. In their analysis, they measured an average surface roughness (Ra) in the range between 8 and 20 µm, and found that the variability was mainly induced by the powder particle size. In particular, the particles sizes were varied between 53 and 149 µm and the results showed that the lowest value of surface roughness was obtained when the smallest powder particle size was used. This behavior was attributed to the presence of unmelted powder particles on the analyzed surface. Peyre et al. (Ref 12), during the deposition of a Ti6Al4V thin wall, showed that surface roughness clearly depends on the unmelted powder particles. Moreover, they found that a reduction in the maximum surface roughness value (Rt) of about 25% was obtained by increasing the laser power from 320 to 500 W. In addition, an improvement in the surface finish could be obtained by reducing the layer thickness and increasing the melt pool volume. However, the average surface roughness remained almost constant. In contrast, Mahamood et al. (Ref 18), during the deposition of Ti6Al4V samples, observed that the average surface roughness decreased when the laser power values increased. Moreover, they also analyzed the effect of the oxygen level, but found no clear relationship between the oxygen level and surface roughness (Ref 12). Resch et al. (Ref 19) deposited Co-based alloy thin walls and found that the average surface roughness decreased when the powder feed rate decreased and the travel speed increased. Later, Mahamood and Akinlabi (Ref 20) confirmed that the surface roughness of Inconel 690 samples increased with the powder feed rate. Lewis and Schlienger (Ref 21) demonstrated the feasibility of the LP-DED process to produce near-net shaped parts of Inconel 690 with a surface roughness of about 12 μm. Gharbi et al. (Ref 22), analyzing thin-wall geometries, identified two types of characteristic roughness along the building direction: micro-roughness and macro-waviness. The former was attributed to particle agglomeration in inter-layer areas and the solidification line, whereas the macroscopic contribution was related to the formation of periodic menisci on vertical surfaces, associated with melt pool stability. Rombouts et al. (Ref 23) studied the effect of laser remelting on surface roughness. In their work, they evaluated the surface quality, in terms of maximum height of the profile (Rt), in two directions, that is, parallel (X-direction) and perpendicular (Y-direction) to the deposition strategy. A clear correspondence between waviness and hatching distance before remelting was identified. However, this correspondence was not observable after remelting. Saboori et al. (Ref 24) studied the effects of deposition strategy on the surface roughness of 316L samples. They showed that surface roughness was not influenced to a great extent by the deposition strategy and that the top surfaces were characterized by a higher surface roughness than the vertical ones.

In addition to the surface quality, distortions can occur due to the generation of high residual stresses during the layerwise building process (Ref 25,26,27), which causes the failure of the manufacturing process or produces a component that does not respect the dimensional requirements (Ref 28). As is typical of metal AM processes, residual stresses are developed in LP-DED due to the large temperature gradients that are induced on the components and the non-equilibrium heating/cooling conditions (Ref 29,30,31,32). Nickel et al. (Ref 33) and Dai and Shaw (Ref 34) showed that residual stresses were influenced by the deposition strategy. Using a finite element model, they observed that residual stresses were reduced for a deposition strategy parallel to the smaller dimension of the substrate or when using an offset-out deposition strategy for large substrates. Corbin et al. (Ref 35) showed that increasing the initial temperature of the substrate, by means of a preheating phase, led to lower residual stress values. Rangaswamy et al. (Ref 36) showed that samples produced by LP-DED were characterized by a compressive state in the core and a tensile state on the edges. Later, the same authors observed that the residual stresses were almost uniaxial and aligned along the building direction (z-axis) (Ref 37). Sun et al. (Ref 38) showed that residual stresses on heat-treated samples were lower than the stresses observed in as-built samples. They found, in particular, that when a stress-relieving heat treatment was used at 600 °C for 40 min, the stresses measured on AISI 4340 samples were reduced from 1200 to 750 MPa. Liu et al. (Ref 39), using the Vickers micro-indentation method, showed that residual stresses were higher in the overlapping region between two adjacent tracks. The higher value of stress in the overlapping region also confirmed a higher stress value in the overlapping region using the hole drilling and the slitting method. Saboori et al. (Ref 24), measuring the residual stresses on cube samples, showed that the stress values on the top surfaces were lower than the stress values measured on the lateral surfaces. Moreover, they observed that the deposition strategy influenced the stresses on the lateral surfaces to a great extent, while the stresses on the top surfaces were almost independent of the deposition strategy, and this was attributed to the different thermal behavior derived from the deposition strategy. Pinkerton et al. (Ref 40) evaluated the effect of the line mass, measured as the ratio between the powder feed rate and travel speed, on the residual stress distribution of IN718 thin walls. They showed that a reduction in the mean level of stress was observed when the line mass was increased and this was related to the higher value of the layer height. Wang et al. (Ref 41) measured the residual stress on AISI 410 thin walls using the neutron diffraction method. They observed that the travel speed had no influence on the stress values and that residual stresses increased as the laser power value increased.

Some information can be drawn from the literature review. First, it may be observed that most of the studies analyzed the surface quality of thin-wall geometries. The analysis of the literature also showed that residual stresses were studied using both numerical and experimental methods, although the investigations were mainly focused on the analysis of the effects of the deposition strategies on the stress distribution in the core of samples and that the investigation of the subsurface residual stresses received only limited attention.

Focusing on the improvement of the overall part quality and in order to obtain a higher level of productivity, the aim of this work has been to clearly identify and understand the relationships between high level process parameters and the surface and subsurface characteristics (Ref 42) of cubic 316L stainless steel samples. Hence, starting from the usual process parameters available in the literature, the process parameter window was appropriately expanded. In particular, the parameters that directly influence the specific energy, such as laser power and travel speed, were varied in the experimental campaign,with all the other process parameters being kept constant, in order to study their effects on surface roughness, dimensional deviations, and residual stresses.

Material and Methods

The following paragraphs describe the material and equipment used for the production of the samples. Subsequently, the approach adopted to evaluate the surface quality and the residual stresses is described.

Sample Geometry

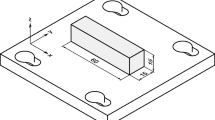
Cubic 20 × 20 × 20 mm3 samples were fabricated on a 60 × 100 × 8 mm3 substrate of the same material for the purpose of this work (Fig. 1). The dimension of the cube was selected considering the UNI EN ISO 4287:2009 (Ref 43) and ASTM E837-13a (Ref 44) standards, which specify the minimum dimensions required to perform roughness and residual stress measurements by the hole drilling method.

Fig. 1
figure 1

CAD model of a 316L cube sample produced by the LP-DED process (all the dimensions are in mm)

Full size image

Sample Production

Gas-atomized 316L stainless steel powder, with a particle diameter of between 50 and 150 μm (D10 = 63.3 µm, D50 = 85.4 µm, D90 =135.2 µm), was used in this work. Most of the powder particles were characterized by a nearly spherical morphology (Ref 45), with only a few particles exhibiting satellites or an irregular shape. Samples were produced using a prototype apparatus, developed in the Borealis European project (Ref 46). This prototype consists of a three-axis CNC unit, with a 1000 × 750 × 500 mm3 building volume, and is equipped with a commercial deposition head. The deposition head uses four axisymmetric nozzles to feed metal powder into the deposition area by means of a flux of carrier gas which, in this case, was nitrogen. The energy source is a 3000 W Ytterbium fiber laser (YLS-3000) with a top-hat energy distribution.

The layer thickness, defined as the programmed distance between two subsequent layers, was set to 0.3 mm. Samples were produced using a bidirectional deposition strategy with a pattern rotation of 90° at each layer. Figure 2 schematizes the deposition strategy used in the experiment.

Fig. 2
figure 2

Representation of the bidirectional deposition strategy used for the sample production

Full size image

In this work, the travel speed and laser power are taken as variables and only one variable is changed at a time by keeping constant all the other parameters. In fact, it was demonstrated that these two parameters directly affect the overall process efficiency by modifying the melt pool energy and the catchment efficiency (Ref 47). Hence, two sets of samples, composed of three cubes each, were produced. In the literature, the commonly used laser power and travel speed values vary between 300 and 500 W (Ref 48,49,50) and 250 and 700 mm/min (Ref 51,52,53), respectively. In this work, starting from high specific energy values of the laser power and of the travel speed, the process parameters window was extended, compatibly with the machine characteristics, in order to obtain a twofold increase in the building rate. Since the process window was specifically identified on the basis of the needs of an industrial company, the process parameters are normalized in this paper, with respect to the higher productivity levels highlighted in the literature review, taken as reference values, to safeguard the confidentiality and secrecy of the Company. Thus, in order to put in evidence the percentage increment in parameter’s values, the levels of process parameters assumed in the DoE were divided by the reference values, that were assumed as the lower limit. The two sets of normalized parameters are detailed in Table 1. Moreover, it should be noted that one sample, that is, Cube 3, is in common between the two sets.

Table 1 Normalized process parameters used for the sample production
Full size table

Surface Quality Measurement

Surface quality was evaluated by considering the dimensional deviation and the surface roughness. In this evaluation, the border zone close to the edges was excluded to prevent edge effects. The dimensional deviation, with respect to the nominal dimension, was evaluated along the X, Y, and Z (building direction) axes using a micrometer.

Surface roughness was evaluated on the top and the lateral surfaces of the LP-DED samples using a portable stylus-type surface roughness tester, RTP80 by SM Metrology Systems S.r.l (Italy). The measurements were taken along a profile length of 12.5 mm (Gaussian filter, cutoff of 2.5 mm).

The strategy used for the surface roughness measurements is illustrated in Fig. 3. In short, the measurements were performed on the lateral surfaces, named Side A, Side B, Side C and Side D, along the building directions (Z-axis), and on the top surface along the Y-axis on each cube. Figure 4 shows a sample during the measuring phase.

Fig. 3
figure 3

Representation of the surface roughness measurement directions on an LP-DED sample

Full size image
Fig. 4
figure 4

Details of the measurement phase (a) on a top surface and (b) on a lateral surface

Full size image

Three measurements (Fig. 3) were performed on each surface and the average value and the standard deviation were then calculated. The following parameters were evaluated for each measurement:

  • Ra (μm) that is the average roughness;

  • Rz (μm) that is the average maximum height of the profile;

  • Rsk that is the skewness parameter;

  • Rku that is the kurtosis coefficient.

Moylan (Ref 54) suggested that the combined use of these four parameters allows a complete description to be obtained of the surface aspect. In detail, Ra represents the average mean deviation of the irregularities from the mean line (Ref 55) and Rz represents the average value of the distance between the highest and the lowest points of the profile calculated in five positions along the length (Ref 55). However, some errors, related to the description of the surface, could occur when only using these two parameters. For example, different surfaces can be described with the same Ra value, although the morphology may clearly be different, since it can represent both a profile with high peaks or one with deep valleys. For this reason, Rsk and Rku, which describe the level of asymmetry of the profile with respect to the mean line and the sharpness of the probability density of the profile, respectively, were introduced into this analysis.

Residual Stress Measurement

The residual stresses were evaluated using the hole-drilling strain-gage method (HDM) (Ref 44). HDM is a semi-destructive method that is widely used to evaluate a residual stress distribution beneath the surface (Ref 56,57,58,59), and it is recognized as being one of the most efficient methods for evaluating residual stress distributions, in terms of cost, accuracy and versatility (Ref 60). In this work, the RESTAN-MTS3000 system (SINT Technology S.r.l, Italy) was used. A 1.2 mm depth-flat was produced, by means of a high-speed air turbine and using a 1.6 mm diameter drill bit, and 24 drilling steps were executed with a penetration depth of 50 µm. The deformations relaxed by the tested material, at each drilling step, were acquired using a K-RY61-1.5/120R (HBM Italia S.r.l., Italy) Type B 3-element rosette connected to an amplifier. The surface of each sample was prepared according to the procedure described by Salmi and Atzeni (Ref 58) and Aversa et al. (Ref 61).

The automatic RSM software (SINT Technology s.r.l, Italy) was used to acquire the deformation for each increment. The acquired deformations were then introduced into the EVAL software (SINT Technology s.r.l, Italy) in order to compute the residual stress profiles according to the ASTM E837-13a (Ref 44) Standard. The residual stress state was evaluated in terms of principal stress and beta-angle. In particular, the beta-angle describes the direction of the maximum principal stress, with respect to the gage a of the rosette, and it is necessary to uniquely define the stress state. In this work, the residual stress distribution was evaluated on the top surface of each cube in two different positions. Figure 5 illustrates the two positions of the rosettes. Figure 6 shows the sample during the measurement phase.

Fig. 5
figure 5

Positions of the rosettes on the top surface of each cube

Full size image
Fig. 6
figure 6

Top surface of a sample during a residual stress measurement phase using the MTS3000 RESTAN (REsidual STress ANalyzer) system by SINT Technology

Full size image

Results and Discussion

In the following paragraphs, the results are described in terms of surface quality and residual stresses. As illustrated in Fig. 7, all the samples were produced successfully. Firstly, the dimensional deviation of the produced sample are presented with respect to the nominal dimension. The surface quality is then analyzed in terms of surface roughness. Finally, the stress beneath the top surface of each sample is discussed.

Fig. 7
figure 7

Samples obtained with different process parameters

Full size image

Surface Quality

The deviations between the actual dimensions and the nominal ones, measured on each sample, are reported in Table 2. The results show that a positive deviation is observed in all the sample. This means that an excess of material is present on all the surfaces, which has to be removed by a post-processing operation.

Table 2 Dimensional deviation measured on the produced sample with different process parameters
Full size table

The deviations measured in Set 1, along the x and y-axes, are equal and increase from 1.0 to 1.5 mm as the travel speed decreases. The deviation along the z-axis is higher and ranges between 1.6 and 2.0 mm. The deviation measured on Set 2, along the x- and y-axes, is almost uniform, with a value of around 1.0 mm; again, the deviation along the z-axis is higher, with a mean value of 1.7 mm.

Comparing the results, it is possible to observe that the dimensional deviation is mainly influenced by the travel speed value, and a decreasing deviation trend is observed as the travel speed increases. Instead, the laser power value does not influence the value of the dimensional deviation to any great extent and the differences are consistent with the accuracy of the measurement instrument.

The obtained dimensional deviation can be explained by considering the effect of the process parameters on the melt pool dimensions. In fact, as demonstrated by Piscopo et al. (Ref 62), the dimensions of the melt pool are affected to a great extent by the process parameter values. A lower specific energy value is obtained when the travel speed is increased, and as a consequence, a narrower melt pool is observed (Ref 62, 63). This causes a lower deviation value with respect to the nominal dimension in the x and in the y directions. Furthermore, as the travel speed increases, a smaller track height value is obtained, and this results in a lower deviation along the z-axis due to the increased travel speed value. Moreover, as demonstrated by Zhang et al. (Ref 64), the effect of laser power on the track width is less significant than the travel speed.

In our study, the dimensional deviation corresponds to the mean value of the melt pool width measured on a single track (Ref 65), and as a result, the selection of the most suitable process parameters, combined with a correct compensation of the deposition head path, could be used to minimize the deviation between the actual and the nominal dimensions.

Figure 8(a) illustrates a comparison between the average surface roughness, Ra, measured on Cube 1, Cube 2, and Cube 3. A comparison between the average maximum height of the profile, Rz, measured on Cube 1, Cube 2, and Cube 3, is illustrated Fig. 8(b). The results show that both Ra and Rz are not affected to a great extent by the travel speed, although it is possible to observe that the minimum data dispersion is obtained on Cube 2. Furthermore, it is possible to observe higher values of Ra and Rz on the Top surface. The values of Ra and Rz on the Top surface are 29.1 μm ± 1 and 149.2 μm ± 7.5, respectively. The mean value of Ra on the lateral surfaces is 21.9 μm ± 2.1, while the mean value of Rz is 115.6 μm ± 10.2.

Fig. 8
figure 8

Comparison between the average surface roughness (Ra) and the average maximum height (Rz) measured on the analyzed surfaces for samples produced with different travel speeds (a,b) and with different laser power values (c,d)

Full size image

The comparisons between the Ra and of Rz values measured on the samples produced with different laser power values, namely on Cube 3, Cube 4 and Cube 5, are illustrated in Fig. 8(c) and (d), respectively. From the obtained results, it can be observed that, in analogy with Set 1, the Ra and Rz values are also almost unaffected by the laser power value for Set 2. The average values of Ra and Rz on the Top surface are 30.8 μm ± 2.4 and 151.2 μm ± 8.9, respectively, for Set 2. The mean value of Ra on the lateral surfaces is 21.7 μm ± 2.7, while the mean value of Rz is 115.8 μm ± 12.4. These values are perfectly aligned with the corresponding ones of Set 1.

The literature results show that, among the various LP-DED parameters, surface roughness is influenced by the laser power and travel speed. However, the majority of the works in the literature analyzed thin-wall geometries. The results obtained in this work show that the surface roughness is not influenced to a great extent by the selected process parameters during the production of a massive component, but it is mainly influenced by the presence of unmelted particles. This result is in agreement with those of Li et al. (Ref 14), Saboori et al. (Ref 24) and Piscopo et al. (Ref 66), who, during the production of 316L samples, showed that the surface quality was influenced by oxidation and powder adhesion on the surface and that the surface roughness was not affected by the process parameters to a great extent.

Figure 9 illustrates a topological map of the Rsk-Rku values. This topological map was initially proposed by Whitehouse (Ref 67) for different cutting technologies. It can be observed that most of the Rks values range between 0.1 and 0.25, but no significant differences can be observed between the lateral and top surfaces. In particular, it is possible to observe that almost all the surfaces of the samples are characterized by a positive skewness parameter value. This means that a high percentage of the surface is below the mean surface and the surface peaks can be attributed to agglomerated powder particles (Fig. 10). Even though negative values of Rks are observed on Side A and Side B of Cube 5 and on Side B of Cube 3, these values are very close to zero, and consequently, a normal distribution can be assumed.

Fig. 9
figure 9

adapted from Tufescu et al. (Ref 68)

(a) Rsk-Rku topological map of the LP-DED process and (b) comparison of the Rsk-Rku values for different manufacturing processes,

Full size image

On the contrary, it is possible to observe that the mean values of Rku on the lateral and on the top surfaces are slightly different, with mean values of 2.9 ± 0.1 and 2.5 ± 0.1, respectively. The Rku distribution on the top surfaces is very narrow. However, it was not possible to identify a clear relationship between the Rsk and Rku values and the process parameters used for sample production, and the data dispersion was therefore attributed to the variability of the process.

A comparison between the results obtained from the LP-DED process, represented by the black points, with the results obtained from different manufacturing processes, is illustrated in Fig. 9(b). It is possible to observe that the obtained values are located between the turning operation and the electrical discharge machining (EDM) process. This means that the morphology of the surface of the LP-DED samples, as described by the distribution of the peaks and valleys, is similar to the morphology of a surface obtained from milling. However, it should be considered that the roughness of these processes could differ a great deal. In fact, the typical value of surface roughness of a milling process is in the 0.8 µm to 3.2 µm range, while we obtained a surface roughness of one order of magnitude higher for the LP-DED samples.

In order to analyze the surface texture in more detail, the roughness profiles measured on the top and lateral surfaces of Cube 4 were compared with the surface maps captured by stereomicrography (Fig. 10). In short, Fig. 10(a) represents the surface morphology and the roughness profile measured on Side A, Fig. 10(b) shows Side B and the roughness profile obtained on this surface of the sample and Fig. 10(c) depicts the top surface of the sample and the relative roughness profile obtained from the measurement.

Fig. 10
figure 10

Comparison between the stereomicrograph image and the filtered roughness profile (cutoff of 2.5 mm) obtained on different surfaces. (a) Side A, (b) Side B and (c) Top surface of Cube 4

Full size image

From these results, it is possible to observe that periodic menisci are present on the Side A surface, leading to a value of Rku <3. The period is about 0.3 mm and it was therefore attributed to the layer thickness. This effect is less evident on Side D, where a value of Rku >3 was obtained. Unmelted particles are clearly visible on both surfaces. The roughness profile may thus be attributed to the presence of unmelted particles (peaks) and to the thickness of the layer used for the production of the sample. In the top surface case, the roughness profile may be related to the hatching distance used during the deposition process. Again, unmelted particles are observed, especially where no overlap between adjacent tracks was obtained during the deposition process.

The layer thickness and the hatching distance, which appear to be factors that influence the surface topology, were maintained constant in the experiments, and this could be the reason for the almost uniform results, in terms of roughness, obtained for the different laser power and travel speed values.

Residual Stresses

Figure 11 shows the tensional state of samples obtained with different travel speeds. The residual stress profile and the direction of the maximum principal stress (σmax) on the top surface of Cube 1 are represented in Fig. 11(a). It is possible to observe that the sample is characterized by an initial compressive state, with σmax that reaches a value of about −100 MPa. The stress then sharply increases and reaches a local maximum value at a depth of about 0.20 mm. After this point, the stresses increase slightly, up to about 300 MPa, until the analyzed depth is reached. The β-value is characterized by an initial positive value of about 50°. After an initial decreasing trend, at a depth of about 0.15 mm, the measured value of β is almost nil and its value remains almost constant until the total analyzed depth is reached. This means that the maximum stress is inclined by 45° in the xy-plane.

Fig. 11
figure 11

Residual stresses and principal stress direction on the top surfaces of samples produced with an increasing travel speed value: (a) Cube 1, (b) Cube 2 and (c) Cube 3

Full size image

Comparing the stress distribution curves, it is possible to observe that the lowest residual stress value is obtained for Cube 1. A higher stress value is observed for Cube 2 and Cube 3, which are characterized by a higher travel speed. This behavior of the stresses was attributed to the lower thermal energy introduced into the sample, due to the lower interaction time between the laser and the material. In fact, a lower temperature of the melt pool is obtained when the value of the travel speed is increased and, as a consequence, a higher value of the temperature gradient is obtained in the sample (Ref 69).

By comparing the stress distribution just below the surface, it is possible to note that almost all the cubes are characterized by an initial compressive stress state. Only on Cube 3 is the maximum stress characterized by an initial tensile stress state. According to Mercelis (Ref 70), two main mechanisms are responsible for residual stresses and they are related to the temperature gradient (TGM) and the cooling down of the molten material. As far as the former aspect is concerned, large temperature differences around the laser spot induce compressive stresses on the upper layer. Conversely, material contraction during the cooling phase induces a tensile stress state on the upper layer.

From the results, it can be observed that surface compressive stresses were measured in most cubes and the prevaling mechanism is thus TGM. However, Cube 3, which was produced with the lowest laser power value and the highest speed value, and consequently the lowest specific energy value, exhibites a different behavior with a surface tensile stress state. In fact, lower temperature and temperature gradient values were obtained in Cube 3 and the main mechanism in this case is therefore associated with cooling down. No significant variations were detected in the distribution of the β-angle. Moreover, it is possible to observe that no significant variations occurred between the two measurement repetitions.

The tensional state of the samples obtained with different laser power levels is illustrated in Fig. 12. The residual stress distribution and the β-value, with respect to the depth measured on sample Cube 3, are illustrated in Fig. 12(a). After the initial compressive tensional state, the stress distribution shows an oscillatory trend and a maximum value of about 450 MPa is observed at a depth of 0.7 mm. After 0.7 mm, an almost constant increasing trend of stress values is observed. The β-value shows an almost constant value of about 10°.

Fig. 12
figure 12

Residual stresses and principal stress direction on the top surfaces of samples produced with an increasing laser power value: (a) Cube 3, (b) Cube 4 and (c) Cube 5

Full size image

By comparing the results, it is possible to observe that an increase in the laser power leads to a mitigation of the residual stresses. This behavior was attributed to the different temperature distributions during the deposition process due to the different laser power values. A lower value of the thermal gradient is obtained when the laser power value is increased, due to heat accumulation, which may explain the lower observed stress value. The results show that the value of β is not affected to a great extent by the laser power value, hence, the maximum stress is inclined by 45° with respect to the xy-plane in all the cubes. Moreover, by comparing the graphs in Fig. 12, it is possible to notice that no relevant variations were observed between the two repetitions.

Conclusion

In this work, the surface and subsurface characteristics of 316L samples, produced by the LP-DED process, as a function of the travel speed and laser power levels, have beenanalyzed through the measurements of the dimensional deviation, roughness and residual stress state. All the samples were successfully produced and were free of evident surface defects, thus proving that all the investigated parameter values were adequate for the production of the parts.

  • A positive deviation, with respect to the nominal dimension, was noticed for all the samples. The deviation value was influenced by the values of the process parameters, in particular that of the travel speed, but less significantly than that of the laser power, and this was attributed to the different specific energy values.

  • A complete analysis of the surface was obtained, thanks to the combination of the average parameters (Ra and Rz) with the parameters that describe the distribution of the profile (Rsk and Rku). The surface roughness was not significantly influenced by the analyzed range of process parameters. The Ra values ranged from between 10 and 30 μm on the lateral surfaces, while the Ra value measured on the top surfaces was instead higher and varied between 30 and 35 μm. The results therefore showed that the formation of periodic menisci on the surfaces led to a value of the kurtosis parameter of less than 3. A larger percentage of the surface was below the mean line in almost all the analyzed samples. The evidence of high peaks was attributed to the presence of unmelted particles on the surface.

  • The top surfaces of all the samples were characterized by an initial compressive state, and a dependence of the extension of this compressive region on the process parameter values was observed. An increasing tensile stress was observed along the depth in all the samples, after the compressive region. The laser power and the travel speed both influenced the stress value. A lower stress value was obtained when a lower travel speed value or a higher laser power value was used.

Further work is recommended to correlate the observed properties with the specific microstructure developed in the samples for the high-productivity parameters.