Introduction

Al-Si alloys are commonly used in the foundry of aluminum–silicon alloys, which may also contain alloying additives. These alloys are characterized by good castability, corrosion resistance, machinability, heat resistance, electrical and thermal conductivity, low density (2.7 g/cm3), thermal expansion and low casting contraction. Al-Si alloys are also characterized by high-strength properties among light alloys. Thanks to these properties, Al-Si alloys have found a wide range of applications, especially in the automotive, aerospace and electrical machinery industries as well as in the production of household appliances.

Current research, aimed at improving the properties of Al-Si alloys, mainly relates to the use, as modifiers, elements from the group of lanthanides and transition metals. From the group of the lanthanides included: La (Ref 1, 2), Ce (Ref 2), Sm (Ref 3), Eu (Ref 4), Gd (Ref 5), Er (Ref 6, 7) or Yb (Ref 8) were tested. The above-mentioned elements or their mixtures used in appropriate amount reduce the size of precipitations of silicon eutectic mixture. A similar effect on eutectics in Al-Si alloys is exerted by transition metals such as Nb (Ref 9, 10), Zr (Ref 11), Sc (Ref 11, 12) or Mo (Ref 13). Other tests carried out over recent years to increase the properties of Al-Si alloys consist in the reduction of hydrogen and nonmetallic inclusions (Ref 14), development of modern heat treatment technology (Ref 15) and the use of specific casting conditions, e.g., high-temperature overheating of the external polymers (Ref 16).

Crystallization of Al-Si alloys determines the grain size reduction, which causes a significant increase in their strength properties. The danger of the intermetallic phase separation in Al-Si alloys containing Cr, Mo, V and W increases with decreasing the thermal conductivity from the casting (Ref 17). Therefore, these additives are not suitable for use in Al-Si alloys cast into sand and ceramic molds. The high rate of heat transfer coefficient from the casting to the pressure mold gives the possibility of supersaturation of α phase with these additives. This should lead to improvement of its strength properties. Accordingly, the addition of Cr, Mo, V and W to Al-Si alloys intended for pressure casting seems to be the most advantageous.

The preliminary tests carried out confirmed the possibility of obtaining higher-strength properties of Al-Si alloys predestined to pressure die casting as a result of the discussed high-melting element additives (Ref 18,19,20,21). The second part of this paper describes the experimental procedure of material studies. Crystallization subjected to modifications through the influence of alloying additives can be described by means of cooling curves. The cooling curve analysis is one of the best methods to assess the quality of casting alloys. On the derivative curve, there are thermal effects from the crystallization. A description of the characteristics points on the derivative curve will be also found in Sect. 3.

The mechanical properties result from alloys microstructure, and then, in Sect. 4 exemplary microstructures obtained with the use of described procedure were presented. There are specific statistical relationships between the characteristic values of derivative and cooling curves, the chemical composition, metallurgical operations, microstructure and mechanical properties. An important advantage of the cooling curve analysis is the short time to evaluate the mechanical properties (short time of the curves registration). The stated problem was to predict mechanical properties on the basis of the cooling curves taking into account a large number of variables (dependent variables and explanatory variables) and nonlinear dependencies. In order to determine the relationship between characteristic points of cooling curves and mechanical properties, data mining techniques were used (Sect. 5). The aim of the task is to analyze the data aimed at acquiring and formalizing knowledge about occurring phenomena (Sect. 6). These phenomena can be described by the induced changes in mechanical properties. Section 7 includes conclusions and final remarks.

Experimental Methodology

The mechanical properties as well as cooling curves were developed on the basis of experimental studies on Al-Si alloy EN AC 46000 grade (EN AC AlSi9Cu3 (Fe)). The range of the chemical composition of the alloy used in the tests is presented in Table 1.

Table 1 Scope of the chemical composition of the initial test Al-Si alloy type EN AC-46000
Full size table

It is a typical hypoeutectic Al-Si alloy predestined to high-pressure die casting (HPDC). Chromium, molybdenum, vanadium and tungsten were added into the Al-Si initial alloy as AlCr15, AlMo8, AlV10 and AlW8 master alloys. This process took place in the holding furnace of the die casing machine. The initial Al-Si alloy was melted in a gas-heated shaft furnace with the capacity of 1.5 Mg. Inside the shaft furnace, the Al-Si alloy was refined with the solid refiner Ecosal Al113.S. After the melting and refinement, the Al-Si alloy was deslagged and transported to the heating furnace placed near the die casting machine. The temperature of the alloy in the heating furnace amounts to 720 °C. The microstructure was tested on the NIKON MA 200 microscope at magnification 100 × for castings from the resin-sand probe and 1000 × in the high-pressure die castings.

Mechanical properties were determined on specimens from high-pressure die castings. For all variants of the chemical composition, pressure die castings of the side cover of the roller shutter casing were made. The shape of this casting resembles a plate with a wall thickness g = 2 mm. To determine the selected properties of silumin, static tensile tests and Brinell hardness measurements were taken. The tensile strength Rm and the elongation A were determined in the static tensile test carried out on an Instron 3382 testing machine at a speed of 1 mm/min. The tensile strength of silumin was determined on specimens taken from the pressure die castings. From one pressure die casting, three test specimens were taken for each of the examined chemical compositions of the silumin. The samples had a flat shape with a rectangular cross section of 10 × 2 mm recommended by PN-EN 1706 standard. Hardness HB was measured with an HPO 2400 universal hardness tester. The following measurement parameters were applied: ball diameter d = 2.5 mm, load of 613 N and static load duration of 30 s.

Cooling curves were determined for castings from the probe made of resin-coated sand. Before it was poured into the probe, the silumin was heated to the temperature of 1100 °C in induction furnace with capacity of 6 kg. The casting from the probe had a shape similar to a cylinder with a diameter of 50 mm and a length of 45 mm. In its thermal center, the type S thermocouple was placed. Combinations of Cr, Mo, V and W additives with concentration up to 0.5% were tested. Cooling curves were recorded to determine their characteristic values: temperature “t” and the first temperature derivative versus time “dt/dτ = K” specified for so-called characteristic points. These points are determined on the derivative curve “dt/dτ = f’(τ)” as local extrema and “zero” points (K = 0 °C/s).

Cooling Curve Analysis

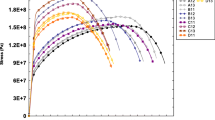
Figure 1 shows the representative cooling curves of multi-component Al-Si alloy. These curves were determined for EN AC-4600.

Fig. 1
figure 1

The representative cooling curves of EN AC-46000 alloy

Full size image

Figure 2 shows the curves for EN AC-46000 alloy with the addition of 0.5% Cr.

Fig. 2
figure 2

The representative cooling curves of EN AC-46000 alloy with the addition of 0.5% Cr

Full size image

Figure 1 and 2 shows two curves: temperature versus time (t = f(τ)) and its derivative (cooling rates versus time—dt/dτ = f′(τ)). As regards the interpretation of curves and points, three thermal effects occur on the analyzed curves: AB—caused by the crystallization of primary dendrites of the α solid solution, BDEFH—the effect of eutectic crystallization “α + β + AlSiFe intermetallic phase” (so-called ternary eutectic), third HKL effect is caused by the crystallization of the complex eutectic “α + β + Al2Cu + AlSiCuFeMgMnNiX” (so-called quaternary eutectic), where X—can be any high-melting element (Cr, Mo, V and W) or its combination. Points: A—maximum thermal effect of α phase crystallization, B—finish of α phase crystallization and start of the ternary eutectic crystallization, D and F—equilibrium in the heat of crystallization of ternary eutectic and heat transfer from casting to the environment, E—maximum thermal effect from ternary eutectic crystallization, H—finish of the ternary eutectic crystallization and start of the quaternary eutectic crystallization, K—the maximum thermal effect from quaternary eutectic crystallization, L—finish of quaternary eutectic crystallization and whole alloy. The data presented in Fig. 1 and 2 show that the chromium does not significantly change the course of cooling curves in the tested concentration range; however, it increases the temperature of phase transformations, mainly the transformation of liquid into α phase. Data on the chemical composition of phases in the described silumin can be found in Ref 22.

In principle, each point (both when analyzing t and K) can affect the properties of the alloy. From the viewpoint of the methodology of cooling curve analysis in pressure foundries, the first point on the curves (A) is the most controversial. This is due to the fact that the foundries prefer not to overheat aluminum alloys in the preheating furnaces, so the temperature of pouring the probe is quite low. The second case of transferring silumin from the furnace to the probe with the shank ladle is not a strictly repeatable process, hence, so is the temperature of pouring the probe. Theoretically, this can be reflected into the recorded temperature value in point A. We were able to obtain the temperature at the moment of pouring the probe with the shank ladle higher by about 100 °C than the temperature in point A. In a case of any doubts, the experiment was repeated. This procedure gives a fairly high reliability in the statistical assessment of the coordinates (temperature and its derivative) of point A. The addition of high-melting additives significantly changes the crystallization start temperature. The first effect on the curves (in our case AB) is generally the most susceptible to changes when high-melting elements are added.

The Microstructure of EN AC-46000 Alloy

On the curves, there are three thermal effects caused by the crystallization of component phases of the studied multi-component silumin:

  • primary α (AB effect),

  • ternary eutectic α + AlFeSi + β (BDEFH effect),

  • quaternary eutectic α + Al2Cu + AlSiCuFeMgMnNiX + β (HKL effect).

In the multi-component alloy casted into resin-sand probe, there are intermetallic phases containing high-melting additives in the quaternary eutectic. The volume fraction of these phases in eutectic and their chemical composition depends on the concentration and the combination of Cr, Mo, V and W. Regardless of their combination and concentration on cooling curves, analogous thermal effects were obtained. However, different coordinate values of individual characteristic points for the assumed concentrations and combinations of alloy additions have been observed. Sample values describing cooling curves of the aluminum alloy with Cr are presented in Table 2. Similar measurements were taken for other additives as well as in mixtures.

Table 2 Values describing cooling curves of Al-Si alloy with Cr
Full size table

The crystallization process of the EN AC-46000 alloy in the shell form (resin-sand probe) starts with the precipitates of dendrite solid solution α (Al) and then the ternary eutectic α + AlFeSi + β. The AlFeSi phases have a characteristic morphology commonly known as “Chinese script.” They may also contain Mn atoms besides Al, Fe and Si. After the ternary eutectic crystallization another, more complex eutectic called quaternary crystallizes. It contains intermetallic phases: Al2Cu and the most complex that which can contain all the elements present in the alloy. It was designated as AlSiCuFeMnMgNi. As a result of the above-described crystallization process, the microstructure shown in Fig. 3 was obtained.

Fig. 3
figure 3

The microstructure of EN AC-46000 alloy in the resin-sand probe

Full size image

The addition of a relatively small amount of high-melting additives into the EN AC-46000 alloy, e.g., 0.1% Cr, does not fundamentally change the crystallization process and the microstructure. Atoms of high-melting additives join mainly to the most complex intermetallic phase (component of the quaternary eutectic). It is described as AlSiCuFeMnMgNiX, where X is high-melting additive or any combination of additives of this type. In Fig. 4, this phase was described as AlSiCuFeMnMgNiCr.

Fig. 4
figure 4

The microstructure of EN AC-46000 alloy with the addition of 0.1% Cr in the resin-sand probe

Full size image

The greater amount of high-melting additives, e.g., 0.2% Cr, changes the crystallization process. It starts with the peritectic crystallization of intermetallic phases containing high-melting additives. After crystallization of intermetallic phases, α (Al) dendrites precipitate. Then, liquid metal crystallizes as plate-shaped ternary eutectic (α + AlFeSi + β). Then, the quaternary eutectic (α + Al2Cu + AlSiCuFeMnMgNiX + β) forms from the residual liquid. Figure 5 shows, for example, the microstructure of Al-Si alloy containing 0.2% Cr, which is the result of the crystallization process described herein.

Fig. 5
figure 5

The microstructure of EN AC-46000 alloy with the addition of 0.2% Cr in the resin-sand probe

Full size image

Further increase in the amount of high-melting additives does not fundamentally change the crystallization process of EN AC-46000 alloy. The effect of increasing the amount of high-melting additives is, however, obtaining a greater number of intermetallic phases containing these additives. This is visible in the EN-46000 alloy containing the 0.5% Cr shown in Fig. 6.

Fig. 6
figure 6

The microstructure of silumin EN AC-46000 with the addition of 0.5% Cr in the resin-sand probe

Full size image

Microstructure of Al-Si alloy obtained in a pressure casting in terms of phase structure is analogous to the microstructure from the shell mold. However, the crystallization process in both cases is characterized by a different rate of heat transfer from the casting. The relatively slow process of heat transfer from the shell mold is much more intensified in the case of pressure casting due to the mass of the pressure mold. This leads to a faster course of the crystallization process in the pressure mold compared to the resin-sand probe. As a consequence, significant refinement of microstructure components is obtained. It is visible when comparing microstructures in Fig. 3 and 7. Another consequence of the intensification of heat transfer from the casting is the possibility of supersaturation of solid solution with the alloy additives. This reduces the volume fraction of intermetallic phases. Due to the considerable refinement of the microstructure components, ternary and quaternary eutectics were marked together. In the microstructure, apart from the area of eutectic, dendrites of the α solid solution are visible.

Fig. 7
figure 7

The microstructure of EN AC-46000 alloy in a pressure die casting

Full size image

The addition of a small amount of high-melting additives, e.g., 0.1% Cr, causes a change in the morphology of β phase. The microstructure of alloy containing about 0.1% Cr shown in Fig. 8 is characterized by a much more compact form of Si precipitates compared to the alloy without Cr. Chromium in Al-Si alloy causes the intermetallic phases crystallization, as well as to some supersaturation of the α solid solution.

Fig. 8
figure 8

The microstructure of EN AC-46000 alloy with 0.1% Cr in a pressure casting

Full size image

The addition of more high-melting additives into the alloy, e.g., 0.3% Cr, causes crystallization of the peritectic phases. An exemplary microstructure of EN AC-4600 alloy containing about 0.3% Cr is shown in Fig. 9.

Fig. 9
figure 9

The microstructure of EN AC-46000 alloy with 0.3% Cr in a pressure casting

Full size image

The above-mentioned intermetallic phases are clearly visible in the microstructure. Their maximum dimensions do not exceed 10 μm. Increasing the content of high-melting additives causes a significant increase in the size. Figure 10 shows the microstructure of Al-Si alloy containing about 0.5% of Cr. The large chromium-containing phases are visible. Their dimensions reach up to ~40 μm.

Fig. 10
figure 10

The microstructure of EN AC-46000 alloy with 0.5% Cr in a pressure casting

Full size image

Mining for the Best Cooling Curves–Properties Relationship Model

The stated problem involves the study of the relationship between registered points and thermal effects on cooling curves and the mechanical properties of the tested specimens. Individual samples differed in chemical composition, in particular in alloy additions. The data set included 86 specimens: 32 variables (12—chemical composition, 16—cooling curves parameters, 4—mechanical properties) were registered for each of them, including chemical composition and content of alloying additions, cooling curve points (temperature and its derivative over time) and mechanical properties such as the tensile strength Rm [MPa], proof stress Rp0.2 [MPa], elongation A [%] and Brinell hardness HB. Chromium, molybdenum tungsten and vanadium were added:

  • individually at a concentration of up to 0.5% (in steps of 0.1%),

  • in pairs in each combination at a concentration of each element up to 0.4% (in steps of 0.1%),

  • three together in any combination at a concentration of 0.25% (in steps of 0.05%),

  • four together at a concentration of 0.25% (in steps of 0.05%).

The part of the data set containing the mechanical properties for the basic silumin with the addition of Cr or Cr and V is shown in Table 3.

Table 3 Part of the data set used for statistical relationships (only for two high-melting additives)
Full size table

Individual parameters (points and effects) of cooling curves affect with different mechanical properties. The effects are a reflection of thermal processes during crystallization, thus reflecting the phenomenon of the formation of individual phases of the microstructure, which is directly responsible for mechanical properties. Capturing basic correlations allows you to select the most important effects to create models. Since all variables are continuous, we could use the Pearson’s correlation coefficient. The results of the study of the influence of temperature-related characteristics of cooling curves on individual properties are presented in Table 4 and Fig. 11. Statistically significant correlations were captured in frames.

Table 4 Correlations between temperature-related characteristics of cooling curves and individual properties
Full size table
Fig. 11
figure 11

Statistically significant correlations (captured in frames) between temperature-related characteristics of cooling curves and individual properties with linear regression fitting

Full size image

The scatter plots with linear regression fitting presented in Fig. 11 present the strength of the relationship between temperature and properties. In addition, scatter plots clearly show that observed dependencies (even those statistically significant) are not linear in nature, and some of them only influence with the fragment of their variability. The relationships between temperature derivative and mechanical properties are similar (Table 5, Fig. 12).

Table 5 Correlations between temperature derivative and mechanical properties
Full size table
Fig. 12
figure 12

Statistically significant correlations (captured in frames) between temperature derivative and mechanical properties with linear regression fitting

Full size image

Considering the observed relations, models were created to determine the tensile strength using various exploratory techniques. Both plain regression methods and those that use discrete space of results were used for prediction. The development of dependencies between cooling curves and mechanical properties using data mining methods can improve the quality control process. Considering the existing tools of inference based on cooling curves, the problem of multivariable regression is often avoided in favor of predicting only the tensile strength (Rm) which is the most important material characteristic (Ref 23). Methods of data mining are not limited to linear models, which often better reflect the physical nature of phenomena than statistical models.

The collection of data mining methods includes the most popular tools such as induction of decision trees, artificial neural networks (ANNs) as well as modern ones such as the support vector machine (SVM) or MARSplines (multivariate adaptive regression splines). Purpose of MARSplines, same as multivariate regression, is to find values of output (dependent) variables based on input (predictive) variables. MARSplines are the development of spline regression technique, where in the range of variability of the dependent variable, simple regression models are constructed with fragments. MARSplines is a nonparametric procedure that does not need any assumptions about the functional dependence of variables dependent on independent variables (Ref 23, 24). The dependence is built from coefficients and so-called base functions, fully determined by data. Section limits (determined on the data basis) determine the “applicability ranges” of individual linear equations (Ref 25).

Artificial neural networks (ANNs) are based on the paradigm of parallel computing. It is a computational architecture composed of simple mathematical apparatuses (perceptrons often composed of McCulloch–Pitts neurons) allowing for simple assignment of output values to input signals. The linear combination of many neurons into three, and sometimes a larger number, layers enables the creation of complex regression models. In turn, the use of radial basis functions allows the creation of RBF networks (ANN-RBF) applicable to nonlinear regression problems with complex relationships (Ref 26, 27).

Regression trees are the method from the induction of decision trees family. The method was used by the authors successfully before (Ref 28, 29). C&RT—classification and regression trees algorithm—is well described in the literature (Ref 30, 31). It allows for prediction of dependent variable value classes when the variable is continuous. The advantage of decision trees in relation to other data mining methods lies in the simplicity of model interpretation as well as in the rule character of results that allow for the creation of intuitive knowledge bases. The tree induction algorithm is iteratively dividing the training data set into partitions, and the division goes on until all the partitions become uniform, which can be determined from the least-squared deviation in the case of regression trees and the cost of resubstitution. During the construction of regression trees, the low value of the resubstitution cost is provided by the dependent variable whose value is close to or equal to the average in a given leaf. The best division of the node is the one in which there is the largest decline in the cost of resubstitution.

Random forest (RF) is a method based on decision trees. The idea is to create complex models composed of multiple decision trees combined into one regression model. Each tree calculates the value for each successive input, and then, the result is averaged. The model is independent of outliers, which was previously a major disadvantage of individual decision trees. Another algorithm based on the concept of decision trees is boosted trees (BT), but the solution is slightly different. In the case of boosted trees, the selected boosted algorithm is used for the construction of subsequent trees. Boosting involves, as in the case of RF, weak learners. At the beginning, the algorithm induces trees without considering the weights of the signals and then increases the weight of observations in the event of a classification error. The next trees are built on the same set of training data, but using the weight of previous trees. This process may require the construction of hundreds of trees in order to minimize the error of an incorrect prediction (Ref 32).

Support vector machine algorithm is a linear classifier, which does not mean that it cannot deal with nonlinear problems and even regression. In order to be able to apply it, first we discretized the result space. A solution to the problem of nonlinearity (when the vectors in the training set are not linearly separable) is the so-called kernel trick—mapping the training vectors to a space of larger dimension, where their linear separability can be expected. The calculations are carried out using kernel functions (Ref 33).

In all of these algorithms, learning proceeds according to a certain pattern: on the basis of a part of data (about 70% of cases), a regression model is built. This model can take a different form: a set of rules, a matrix of distances, weights on connections, or a matrix of vectors. The above-mentioned models are tested in the learning process with approx. 15% of cases, and its final form is validated (verified) using the last separate group of data—approx. 15%. The division of the training set according to schemes 70-15-15 was dictated by a relatively small size of data set. Seventy percentage of bing observations for learning seem to be exaggerating. It is a bit more than in bootstrap methods where about 63% is drawn. The models can be evaluated using several parameters, including correlation coefficient. The final operation can be tested for consistency of matching results with the input data of the dependent variable. The process of machine learning or discovering knowledge can be symbolically represented in three steps: (1) discovering knowledge in data (Ref 34); (2) prediction–creation of prognostic models (Ref 35); (3) creation of knowledge bases—codification of results for future use (Ref 36). The developed models will be able to continue autonomous learning during industrial processes.

Regression models, MARSplines, ANN-RBF, C&RT, BT, RF, SVM, were developed and tested for the same problem (Rm prediction), on the same learning data set. Results are presented in Table 6.

Table 6 Models performance on Rm dependent variable. Best results bolded
Full size table

Best results were obtained with the C&RT algorithm; therefore, it was used in further analyses.

Regression Trees for Properties Prediction

The smallest error means the best fit of the model to measurements and the best quality of prediction. Decision trees best-coped with the nonlinearity of the problem and at the same time best-reflected the different strength of correlation in different areas of variability of cooling curves.

The degree of the fitting (quality of the model prediction, Table 4) in the case of decision trees compared to the other models may result from several premises. One of those is the ability of the use of various explanatory variables in individual (differentiated) ranges of variability of a dependent variable. The selection of a variable to the model is not dictated by its correlation with the dependent variable calculated for the whole set, as in the case of multiple regression. C&RT selects variables for divisions at the time of the test, which means that each time only the partition of the learning set on which the division takes place is taken into account. In special cases, nonlinear dependencies, some variables may have significant significance, but only in a small area of variation. This situation also applies to this case—the DTA characteristics are the most influential in the area of the AB effect, and the next piles are only in certain (limited) ranges, what is already indicated in Table 2.

An algorithm of the C&RT tree allows not only creating the decision rules in the form of tree, but also determining the validity of individual predictive variables. Variable is considered important in the regression process, i.e., carrying information about the dependent variable, if this variable often participates in the process of dividing objects from the training set. The attribute “readiness” to participate in the tree-building process is measured during the construction of the trees. On this basis, the model makes the ranking of variables in respect of their weights. Importance means a high degree of covariance (expressed as covariance or correlation) of a given factor with the dependent variable (Fig. 13).

Fig. 13
figure 13

The importance of predictors calculated with different algorithms

Full size image

Trees allow a graphical representation of these rules in a user-friendly way. As a result, we obtain a tree model in which each arc represents a test on the independent variables and each node (leaf) represents a single class of dependent variable values (Fig. 14). Tree-building algorithm partitions a set of learning objects (samples) iteratively on the basis of independent variables until each partition contains the data belonging to one class (of dependent variable). The partitioning in C&RT algorithm for the regression tree is based on the criterion of least squares (least square deviation—LSD).

Fig. 14
figure 14

The C&RT regression tree form for the variable Rm

Full size image
$$R(t) = \frac{1}{{N_{w} (t)}}\sum\limits_{i \in t} {w_{i} f_{i} (y_{i} - \bar{y}(t))^{2} }$$
(1)

where

  • Nw(t)—the weighted number of cases in node t,

  • wi—the value of the weighing variable for the case i,

  • fi—the value of the variable frequency,

  • yi—the value of the variable output.

Algorithm of induction of decision trees allows to generate rules for the variability of the indicated dependent variable based on data sets covering the independent variables (predictors) describing the objects (cases). For dependent variable Rm: seven classes can be derived. The classes receive the ID according to the number of the leaf from the regression tree (Fig. 14). The highest strength values have the class with the number ID = 11, for which the rule looks as follows:

$$\begin{aligned} {\text{tB}} > 571.95 \wedge ({\text{KE}} & \le 0.095) \wedge ({\text{KD}} > - 0.005) \wedge ({\text{KK}} > - 0.365) \\ & \Rightarrow [{\text{ID}}11;{\text{Mean}}(R_{m} ) = 266.72;{\text{Var}}(R_{m} ) = 507.56]. \\ \end{aligned}$$
(2)

This formula, along with a set of other rules, allows us to predict Rm in an automatic way, directly on the basis of the DTA curve.

Each class determines the average for the dependent variable (Rm) in the context of the metric conditions for the samples that belong to the class. Within each class, a calculated variance is a measure of dispersion from the mean of samples within the class. In this way, the tree separates the classes of objects with a similar value of Rm. Being a model of one variable, it allows for grouping of objects, which in turn makes it possible to determine in each class the predicted values of other mechanical properties (Table 7).

Table 7 Mechanical properties for individual classes in the C&RT model
Full size table

To determine how those classes differ from each other, the ANOVA was used (Fig. 15). The first graph (a) shows raw data, and the chart on the right (b) shows the calculated characteristics: mean and deviations in classes. ANOVA allows calculation of the average in each of the groups designated by relevant factors. Classes have different frequencies, which affects the variance. The most numerous are classes 8 and 11, which makes them most representative; however, their characteristics are similar. To test whether the differences between them are statistically significant, the NIR (ANOVA) test was used. Results of the test are presented in Table 8.

Fig. 15
figure 15

ANOVA results for classes of C&RT regression tree for the variable Rm

Full size image
Table 8 Statistical significance of differences (p value) between classes
Full size table

We can observe (Table 6) no statistical difference between classes 11 and 12 (in Rm values); however, these groups are differentiated by other mechanical properties (e.g., HB); therefore, their distinction will be important from the perspective of forecasting.

We can use the obtained model to predict mechanical properties, not only Rm, but also other variables (Rp0.2, A, HB). For each property, a separate model was built in an analogous manner to that shown above. In the presented example for Rm, the selected as an example class, ID11 is characterized by the highest properties, and it is also strongly represented (a large number of objects in the class). The results normalized means (for visualization reasons) of properties in each class are presented in Fig. 16 (Fig. 17).

Fig. 16
figure 16

Result properties for classes of C&RT regression tree

Full size image
Fig. 17
figure 17

C&RT regression tree fitting to the observed data

Full size image

Conclusions and Final Remarks

The data presented in the paper indicate that it is possible to create a prediction model of multi-component Al-Si alloy properties based on cooling curves. Decision trees allow you to create models with the highest fitting. Regression trees has advantages: (1) by modeling one dependent variable, we can obtain prediction rules for other mechanical properties in each variation class; (2) the ability to perform statistics (and tests) for classes; (3) capturing dependencies in different ranges of parameter variability (detection of dependencies whose significance is too small in other algorithms); (4) trees make discretization of spaces in search of homogeneous areas; (5) the generated rules give the possibility of simple interpretation and prediction.

The results of calculations and their verification based on test data have been presented. It has been shown that the method of prediction of properties based on regression trees can be used in research works. The development of a prototype IT tool enabling automatic prediction in online mode during the DTA analysis in the future will allow validation of results in order to calibrate the algorithm parameters to improve the fitness. Determination of the stability of the solution, as well as the development of rules for the quantitative impact of alloying additives, will be possible in full, after obtaining more samples for testing.