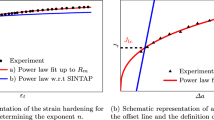
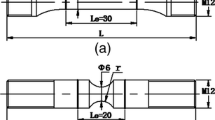
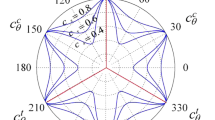
Abstract
Ductile damage model has been widely regarded as a valuable method to predict the failure of sheet metal. Based on the thermodynamic theory and continuum damage mechanics, the fully coupled ductile damage model can be developed, which also can better predict the initiation and growth of the fracture. But the identifications of model parameters with theoretical methodology are difficult due to the complex coupling relationships existing among all state variables. The inverse methodology is regarded as a good method to resolve the problem. In this paper, the recently proposed fully coupled ductile damage model is chosen to investigate the deformation behavior of DP600 steel, in which the mixed saturation isotropic and kinematic hardenings are taken into account and fully coupled with the ductile damage. During the identification process, the least square formula of the error between experimental and numerical results is selected as the target function. The trust region algorithm and genetic algorithm are used with the help of MATLAB for the identification of three damage parameters. Finally, by comparing the experimental and numerical results, the validations of two algorithms are proved. The efficiency of the optimization process with trust region algorithm is higher, but with lower accuracy. Meanwhile, the optimization process is greatly affected by the chosen initial values of the ductile damage parameters.






Similar content being viewed by others
References
Y. Bai and T. Wierzbicki, A New Model of Metal Plasticity and Fracture with Pressure and Lode Dependence, Int. J. Plast., 2008, 24(6), p 1071–1096
Y. Lou et al., New Ductile Fracture Criterion for Prediction of Fracture Forming Limit Diagrams of Sheet Metals, Int. J. Solids Struct., 2012, 49(25), p 3605–3615
D. Mohr and S.J. Marcadet, Micromechanically-Motivated Phenomenological Hosford-Coulomb Model for Predicting Ductile Fracture Initiation at Low Stress Triaxialites, Int. J. Solids Struct., 2015, 67-68(1), p 40–55
Z. Yue et al., Identification of Fully Coupled Anisotropic Plasticity and Damage Constitutive Equations Using a Hybrid Experimental–Numerical Methodology with Various Triaxialities, Int. J. Damage Mech., 2015, 24(5), p 683–710
L. Xue, Constitutive Modeling of Void Shearing Effect in Ductile Fracture of Porous Materials, Eng. Fract. Mech., 2008, 75(11), p 3343–3366
K. Nahshon and Z. Xue, A Modified Gurson Model and Its Application to Punch-Out Experiments, Eng. Fract. Mech., 2009, 76(8), p 997–1009
J. Lemaitre, A Continuous Damage Mechanics Model for Ductile Fracture, J. Eng. Mater. Technol., 1985, 107(1), p 83–89
J.L. Chaboche, A Review of Some Plasticity and Viscoplasticity Constitutive Theories, Int. J. Plast., 2008, 24(10), p 1642–1693
Y. Wen, Failure Analysis of a Sheet Metal Blanking Process Based on Damage Coupling Model, J. Mater. Eng. Perform., 2013, 22(11), p 3288–3295
T.S. Cao et al., A Lode-Dependent Enhanced Lemaitre Model for Ductile Fracture Prediction at Low Stress Triaxiality, Eng. Fract. Mech., 2014, 124-125, p 80–96
H. Badreddine, K. Saanouni, and A. Dogui, On Non-associative Anisotropic Finite Plasticity Fully Coupled with Isotropic Ductile Damage for Metal Forming, Int. J. Plast., 2010, 26(11), p 1541–1575
P. Muñoz-Rojas, E. Cardoso, and M. Vaz, Parameter Identification of Damage Models Using Genetic Algorithms, Exp. Mech., 2010, 50(5), p 627–634
S. Ghosh, M. Li, and A. Khadke, 3D Modeling of Shear-Slitting Process for Aluminum Alloys, J. Mater. Process. Technol., 2005, 167(1), p 91–102
M. Abendroth and M. Kuna, Determination of Deformation and Failure Properties of Ductile Materials by Means of the Small Punch Test and Neural Networks, Comput. Mater. Sci., 2003, 28(3-4), p 633–644
A. Peters, J.G. Chase, and E.E. Van Houten, Digital Image Elasto-Tomography: Combinatorial and Hybrid Optimization Algorithms for Shape-Based Elastic Property Reconstruction, IEEE Trans. Biomed. Eng., 2008, 55(11), p 2575–2583
Z. Yue et al., Identification of Fully Coupled Anisotropic Plasticity and Damage Constitutive Equations Using a Hybrid Experimental-Numerical Methodology with Various Triaxialities, Int. J. Damage Mech., 2015, 24(5), p 683–710
L. Ying et al., Parameter Calibration of GTN Damage Model and Formability Analysis of 22MnB5 in Hot Forming Process, J. Mater. Eng. Perform., 2017, 26(11), p 5155–5165
L.-Y. Wang and L. Li, Parameter Identification of GTN Model Using Response Surface Methodology for High-Strength Steel BR1500HS, J. Mater. Eng. Perform., 2017, 26(8), p 3831–3838
Z.Y. Yin et al., An Efficient Optimization Method for Identifying Parameters of Soft Structured Clay by an Enhanced Genetic Algorithm and Elastic-Viscoplastic Model, Acta Geotech., 2017, 12(4), p 1–19
P.O. Bouchard, J.M. Gachet, and E. Roux, Ductile damage parameters identification for cold metal forming applications, in AIP Conference Proceedings (AIP, 2011)
J. Yan and W. Wu, Identification Method of Shear Stress Constitutive Parameters of Ti-Alloy Thin-Walled Tube, Acta Aeronaut. Astronaut. Sin., 2016, 37, p 2884–2894
G. Syswerda, Uniform crossover in genetic algorithms, in International Conference on Genetic Algorithms (1989)
Acknowledgments
This research was carried out under the financial supports from National Natural Science Foundation of China (No. 51605257), China Postdoctoral Science Foundation Funded Project (2018M642652) and Future Plan Project for Young scholars of Shandong University (2017WHWLJH06).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Cao, K., Yue, Zm., Zhao, Xd. et al. Hybrid Inverse Parameter Identification of Fully Coupled Ductile Damage Model for Steel Sheet DP600 with Two Different Algorithms: Trust Region and Genetic Algorithms. J. of Materi Eng and Perform 28, 3149–3156 (2019). https://doi.org/10.1007/s11665-019-04087-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11665-019-04087-y