Effects of La₂O₃ Addition into CaO-SiO₂ Slag: Structural Evolution and Impurity Separation from Si-Sn Alloy

Abstract

Boron (B) and phosphorus (P) are the most problematic impurities to be removed in the production of solar-grade silicon by the metallurgical process. In this work, the distribution of B and P between CaO-(La₂O₃)-SiO₂ slags and Si-10 mass pct Sn melt was experimentally studied. B distribution coefficient increased from 2.93 in binary CaO-SiO₂ slag to 3.33 and 3.65 with 2 and 10 mass pct La₂O₃ additions, respectively. In the followed acid-leaching experiments, the slag-treated Si-Sn alloys exhibited higher B and P removal than that of the initial alloy without slag treatment. Molecular dynamics simulations were performed to study the effect of La₂O₃ addition on the slag structural and transport properties. A novel oxygen classification method was proposed to distinguish the different structural roles of La and Ca in the CaO-La₂O₃-SiO₂ system. It was found that La³⁺ prefers to stay in the depolymerized region, mostly connects with 6-7 non-bridging oxygen, and requires a weak charge compensation with Ca²⁺. Possible silicothermic reduction was evaluated to discuss the slag chemistry and the mass transfer between slag and metal phase. A thermodynamic model was derived to theoretically study the alloying effect on impurity distribution in slag refining where positive interaction coefficient and high alloying concentration were found most beneficial to improve the impurity removal.

Introduction

SOLAR energy has become the most popular and fastest-growing renewable energy resource worldwide. However, in the current solar-grade silicon (SoG-Si) production, the energy consumption and carbon footprint still remain relatively high by the dominant modified Siemens process and the fluidized bed reactor process. In recent years, carbon neutrality has become the consensus of the international community. For instance, the goal of net-zero carbon emission in the EU wide by 2050 has been endorsed by the European Council to be set in legislation through the first European climate law.[1] China has also announced its national roadmap to achieve the carbon neutrality before 2060.[2] Thus, it has become an urgent challenge and opportunity for the photovoltaic industry and metallurgists to develop a more sustainable and environmentally friendly process for the heavy demand on SoG-Si production. As an evolving technique for the alternate SoG-Si production, the metallurgical process has received increasing attention due to its low carbon emission and low energy consumption.[3] Taking the ELKEM solar process developed in Norway as an example,[4] around 60 pct energy consumption and 90 pct CO₂ emission can be reduced through the combination of metallurgical refining techniques, respectively, slag refining, acid leaching, and directional solidification. In the above refining techniques, slag refining[5,6,7] and acid leaching[8,9] are targeted for the removal of the most challenging impurities boron (B) and phosphorus (P) from the crude metallurgical-grade silicon (MG-Si).

Table I Atomic Charges and Interatomic Parameters of the Teter Potential

Table II Composition of Simulated CaO-La₂O₃-SiO₂ Slag and the Input Atom Numbers

Table III Experimental Data for B and P Distribution of Investigated Slags at 1873 K (1600 °C)

Table IV Measured Impurity Composition of Si-Sn Alloys Before and After Slag Treatment (ppmw)

Table V Calculated Bond Length and Pair Distance of Atom Pairs From MD Simulation

Table VI Calculated Average Coordination Numbers of Atom Pairs From MD Simulation

Table VII Definition of the Novel Classified Oxygen Species With the Focus on the Multiple Network Modifiers Silicate System by Taking the CaO-La₂O₃-SiO₂ System as an Example in the Structural Analysis After MD Simulation

Table VIII Calculated Fraction of Classical and Novel-Defined Oxygen Species From MD Simulation

Table IX Calculated Thermodynamic Parameters According to the Measured Composition of Slag-Refined Si Alloys by FactSage Using FTlite Database

Table X Estimated Thermodynamic Parameters of Slag Components Under Assumed Equilibrium State at 1873 K (1600 °C)

It is difficult to remove B through segregation-based refining techniques like directional solidification and acid leaching because of its high segregation coefficient (k_B=0.8[10]), which is defined as the concentration ratio between solid phase and liquid phase. Nevertheless, slag refining is known as an efficient technique to remove B impurity from the Si melt through oxidation reactions by the oxidizing molten slag. To date, considerable work has been done to investigate the effect of slag properties on the B removal efficiency. A number of slag systems have been studied and reviewed,[7,11,12,13,14] such as CaO-SiO₂,[15,16,17,18,19] CaO-MgO-SiO₂,[20,21,22] CaO-BaO-SiO₂,[6,18] CaO-Na₂O-SiO₂,[5,23,24] CaO-ZnO-SiO₂, CaO-Al₂O₃-SiO₂,[25,26,27] CaO-MgO-Al₂O₃-SiO₂,[28,29] CaO-SiO₂-CaCl₂,[30,31,32] CaO-SiO₂-CaF₂,[24,33,34]and so on. The B removal ability of different slags can be evaluated by the widely used B distribution coefficient (L_B) between the slag and metal in molten state:

$$ L_{B} = \frac{({\text{pct}} \,B)}{[{\text{pct}}\, B]}, $$

(1)

where (pct B) and [pct B] represent the mass fraction of B in slag and Si phases, respectively. The L_B values are affected by the slag composition and change from 2 to 3 for many silicate slags. For instance, Jakobsson and Tangstad[15] reported that the L_B value slightly increases with increasing CaO/SiO₂ ratio. After normalizing the B distribution coefficient by oxygen partial pressure, Johnston and Barati[35] found that higher basicity is favorable for the B removal. Teixeira et al.[16] demonstrated that the slag basicity strongly influences the activity coefficient of boron oxide. Additionally, it was also found that the thermodynamic properties of B₂O₃ were also affected by the local structure of slag. Sakamoto et al.[36] found that the increasing theoretical optical basicity leads to the distinct decrease of the relative fraction of [BO₄] and decreases the activity of B₂O₃ in slag. As investigated by Kline et al.,[37] the increasing B₂O₃ content in slag leads to the transformation from Q² species to Q³, and the B cation is more likely to react with basic oxygens. Similar results have also been reported by Qian et al.[38] that the Q⁰, Q¹, and Q² species play an important role in incorporating B into the Si network and facilitate the formation of Q³ species when the optical basicity of a CaO-Na₂O-SiO₂ slag is lower than 0.66. Recently, Hou et al.[39] investigated the rare-earth oxides (La₂O₃ and CeO₂) addition into CaO-SiO₂ slag, and increasing B removal from MG-Si was observed. Instead of changing slag composition, it has also been shown that significantly higher L_B can be achieved by the slag treatment of alloyed Si such as Si-Sn,[40,41,42] Si-Cu,[43,44] and Si-Fe,[27,45] alloys. Taking into account the research by Ma et al.,[40] the CaO-SiO₂-CaF₂ slag treatment of Si-Sn alloys revealed that the L_B value remarkedly increased from 2 to 200 with increasing Sn addition into Si. Additionally, in the research of Al-khazraji et al.,[42] 93.9 pct B removal was achieved through the CaO-SiO₂-CaCl₂ slag treatment of Si with Sn addition, followed by acid leaching of the refined Si-Sn alloy. Nevertheless, the hidden mechanism still needs to be further investigated.

Stimulated by the previous research, the present work was carried out to investigate the structure–property–composition relationships of the slag-refining process and shed light on the alloying effect of Si on impurity distribution. The CaO-La₂O₃-SiO₂ slag system was investigated for the scientific reasons that the high optical basicity of rare-earth oxide La₂O₃ and the high field strength trivalent cation La³⁺ may bring significant effect on the slag structure evolution and impurity removal in slag refining. Molecular dynamics simulation was also applied to decipher the structural role of La₂O₃ and further used in association with the discussion of B and P removal. In addition, the thermodynamics of solute elements in the refined Si-Sn alloy was discussed and further linked to the impurity segregation and the followed acid-leaching performance.

Methodology

Experimental

The Si-10 mass pct Sn master alloy was prepared through the melting-casting approach by mixing Si and high-purity Sn in a dense graphite crucible placed in an induction furnace. The initial Si source used for this work is the mixture of commercial MG-Si lumps (40 mass pct) with impurity-free Si granules (60 mass pct) produced by fluidized beds (FBR-Si). After melting, the Si-Sn melt was cast in a water-cooled copper mold to attain a homogeneous composition. The obtained Si-Sn master alloy (B: 16.7 ppmw, P: 5.6 ppmw) was further crushed and pulverized by a tungsten carbide ring mill.

A CaO-SiO₂ master slag was obtained by mixing the reagent grade CaO powder (99.9 pct purity, Sigma-Aldrich) and ultra-high-purity SiO₂ fines with an equimolar ratio in a graphite crucible that followed by the melting-casting approach in the induction furnace as well. The master slags were also milled by the tungsten carbide ring mill to fine powders and then melted and cast with 2 mass pct and 10 mass pct reagent grade La₂O₃ powder (99.9 pct purity, Sigma-Aldrich) addition. All the obtained slags were milled to fine powders for homogenization before slag refining experiments.

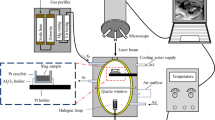
In the slag-refining trials, 20 g Si-10 mass pct Sn powders and 20 g slag powders were mixed into a dense graphite crucible and further placed inside the induction furnace chamber. Before heating, the pressure inside the furnace chamber was evacuated to lower than 10⁻¹ mbar three times and re-filled with pure Ar flow (99.999 pct purity). During the whole slag-refining period, the chamber pressure with Ar flow was kept in 1030-1050 mbar. The schematic presentation of the slag-refining research is presented in Figure 1. The refining temperature was measured by a type C thermocouple and fixed at 1873±20 K (1600±20 °C) for 1 h in association with the electromagnetic stirring and then cooled down to the room temperature. After experiments, samples were cut longitudinally for further metallographic analysis and acid-leaching experiments.

Fig. 1

Experimental procedure and obtained sample cross-sectional image of slag refining

The leaching trials were performed to further purify silicon by dissolving the precipitated impurities in acidic solution. The leaching conditions and parameters were determined based on our previous work.[46,47] The slag-refined Si-Sn alloys were further milled and sieved to a particle size 0.1-0.6 mm. About 2 g milled alloy particles were placed into perfluoroalkoxy alkane (PFA) bottles with 10 mL diluted aqua regia at 333 K (60 °C) in an ultrasonic bath. After 2 h leaching, samples were carefully collected and washed with deionized water and ethanol.

The compositions of obtained slags and Si materials at each stage were measured by high-resolution inductively coupled plasma mass spectroscopy (ICP-MS, Agilent 8800). It is worth mentioning that the accuracy of measured slag compositions was affected by CaO and La₂O₃-related precipitations, which occur when the fully digested solution cooled down to room temperature. Thus, the final slag compositions are not given. However, the analysis of impurity distribution should not be affected since the measured B and P recovery are close to 100 pct and the amount of transported Ca and La into Si phase was measured as negligible. After slag refining, the metallographic samples of Si-Sn alloys were prepared and observed by scanning electron microscope (SEM) and secondary-ion mass spectrometry (SIMS). 2D elemental distributions were measured by SIMS using CAMECA IMS 7f microanalyzer. The measurements were performed in the imaging mode using 10 keV O ⁺₂ ions as the primary beam.

Molecular dynamics simulation

Molecular dynamics (MD) simulations were performed using the LAMMPS package.[48] The well-established Buckingham potential was employed for the description of atomistic interactions as shown in Eq. [2]. The parameter set developed by Teter[49] was adopted for the simulation of CaO-La₂O₃-SiO₂ system and listed in Table I. To better reveal the structural role of La₂O₃ in slag, in total, 7 slags were designed with the addition of La₂O₃ up to 30 mass pct (7 mol pct). Detailed information of simulated slags can be seen in Table II. For each simulation, random configurations with around 8000 atoms were initially generated and equilibrated at 4000 K (3727 °C) for 20 picosecond (ps) in a cubic simulation box with periodic boundary, as shown in Figure 2. The cut-off distances for both Buckingham and Coulombic interactions were set as 11 Å, and the staggered PPPM (particle-particle particle-mesh) solver was adopted for the long-range calculations. The verlet leapfrog algorithm was applied for the integration of motion equations with a timestep fixed at 1 femtosecond (fs). After initial equilibrium at 4000 K (3727 °C) under isobaric-isothermic ensemble (NPT), the temperature was then cooled down to 1873 K (1600 °C) with 1 K/ps under NPT ensemble. At 1873 K (1600 °C), the slag systems were further equilibrated for 50 ps under NPT ensemble and under canonical ensemble (NVT) for another 50 ps. A final 2 nanosecond (ns) production run was performed under NVT ensemble where slag configurations were collected, and the mean square displacements (MSD) were also calculated for the diffusion analysis.

Fig. 2

Overview of the simulation and analysis process relevant to the slag-refining system. Oxygen, Silicon, Calcium, and Lanthanum are, respectively, in red, yellow, cyan, and pink (Color figure online)

$$ U_{ij} \left( r \right) = \frac{{z_{i} z_{j} e^{2} }}{{r_{ij} }} + A_{ij} e^{{ - r_{ij} /\rho_{ij} }} - \frac{{C_{ij} }}{{r_{ij}^{6} }}. $$

(2)

Results

Slag-Refining Results

Experimental results of the B and P distribution are presented in Table III and Figure 3. The theoretical optical basicity of slags is calculated using Eq. [3]:

Fig. 3

Variation in distribution ratio of B and P after slag refining

$$ \varLambda = \frac{{\sum x_{i} n_{i} \varLambda_{i} }}{{\sum x_{i} n_{i} }}, $$

(3)

where $\varLambda_{i}$ is the theoretical optical basicity of pure oxide substance (CaO:1, SiO₂:0.48, and La₂O₃:1.18[50]) and x_i, n_i represents the mole fraction and the number of oxygen atoms in each oxide component. It is seen that the B content in the metal phases significantly decreases from initial 16.7 ppmw to around 4 ppmw after slag refining and the L_B value gradually increases from 2.93 to 3.65 with increasing La₂O₃ addition. As reported by Jakobsson and Tangstad,[15] the L_B value ranges 2.0-2.5 in binary CaO-SiO₂ slag refining with Si at 1873 K (1600 °C), thus, the obtained results suggest that the Sn addition improves B removal.

As can be seen in Table III, the P content in the metal phase inversely increases after slag refining, which is mainly owing to the high P impurity content in the raw material CaO. The L_P value slightly increases from 0.29 to 0.40 after 2 mass pct La₂O₃ addition, but insignificant change was found with higher La₂O₃ addition by 10 mass pct.

The measured chemical composition of other impurities in the Si materials before and after slag refining in Table IV shows the mass transport of the other elements between the slag and metal phases. Mass transport of Ca and La from slag phase to the metal phase is clearly observed and increases with increasing slag optical basicity. Similar trend is also seen for the Fe and Ti impurities. Additionally, it can be noticed that high basicity slag benefits for the Al impurity extraction from the metal phase but limits the Sn loss from metal phase.

Microstructure of Refined Si-Sn Alloy

As Ca and La was transferred from the slag phase to the metal phase, it is worth investigating the alloy microstructure after slag refining. In addition, the alloy microstructure plays an important role in the acid-leaching process as well. As shown in Figure 4, the precipitate types vary with the treatment of different slag compositions. Owing to the small segregation coefficients, metallic impurities were enriched in the Sn phase after solidification. The composition of each precipitate was measured by EDS point analysis. A Fe-Si phase was found as a common precipitate in all alloys, and its minor Ti impurity appears most likely as a solid solution. Additionally, in the Si-Sn alloy refined by CaO-SiO₂ slag, Ca-Sn binary phase was also detected with the stoichiometry close to CaSn₃, while in the two La₂O₃-bearing slag-refined alloy samples, ternary Ca-La-Sn phase was found as the precipitates of Ca and La. However, it is worth mentioning that a large amount of oxygen on the surface of La-bearing phase was also detected, which is probably due to the oxidation of highly reactive La element during the metallographic sample preparation. As the present work focuses more on the impurity removal, more precise work is recommended for a better understanding of the phase equilibria of the REE-containing ternary system.

Fig. 4

Microstructure of precipitates with corresponding element distribution in the Si-10 mass pct Sn alloy after slag refining (a) slag CS-treated alloy, (b) slag CS-2La-treated alloy, (c) slag CS-10La-treated alloy. Ca distribution not presented due to signal noise

The B content in the Si-Sn alloys is only with several ppmw levels, where the accuracy from EDS is generally not reliable. Thus, SIMS elemental mapping analysis was performed for the elements Sn, Ca, La, and B. Figure 5 represents that both Ca and La segregated in the Sn-based precipitate. Additionally, it is also observed that the segregation of B is associated with Ca and La in the Si-Sn alloy. Even though it is difficult to distinguish whether or not B was attracted by Ca and La, direct evidence was obtained for improved B removal in the subsequent acid-leaching process of the slag-treated Si-Sn alloys.

Fig. 5

SIMS elemental mapping of Si-Sn alloy after slag treatment by the CS-10 mass pct La₂O₃ slag

Leaching Results

In the ELKEM Solar process, acid-leaching targets on the removal of P removal and large extent of metallic impurities. To further evaluate the leaching performance of the slag-treated Si-Sn alloys, the leaching efficiency was calculated based on Eq. [4]:

$$ {\text{Leaching}}{\mkern 1mu} \,{\text{efficiency}} = {\text{ }}\frac{{C_{{{\text{after}}{\kern 1pt} {\text{slag}}{\kern 1pt} {\text{treatment}}}} - C_{{{\text{after}}{\kern 1pt} {\text{leaching}}}} }}{{C_{{{\text{after}}{\kern 1pt} {\text{slag}}{\kern 1pt} {\text{treatment}}}} }} \times 100{\text{pct }}, $$

(4)

where the $C_{{\text{after}}\,{\text{slag}}\,{\text{treatment}}}$ and $C_{{\text{after}}\,{\text{leaching}}}$ are the impurity concentrations in the Si-Sn alloy after slag refining and the final impurity concentration in leached Si, respectively. In the leaching of Si-Sn alloy without slag treatment, the B concentration only reduced from the initial 16.7 ppmw to 16.1 ppmw. However, the B removal significantly improved for the alloys after slag treatment. The final obtained B concentration was as 3.4, 3.2, and 3.1 ppmw in the leached alloys treated by slag CS, CS-2La, and CS-10 La, respectively. Thus, as shown in Figure 6, the corresponding leaching efficiency was calculated as 29.9 pct, 30.0 pct, and 25.1 pct. As the difference of B leaching efficiency is insignificant, it should be fair to consider that the leaching efficiency for B is at the equivalent level for the studied alloys.

Fig. 6

Impurity removal efficiency by acid leaching of different Si-Sn alloys

The removal of P exhibits more slag dependent as the final P concentration in leached materials was measured as 12.6, 8.8, and 5.7 ppmw, which decreases with increasing La₂O₃ addition in the slag. Accordingly, the leaching efficiency of P was significantly improved from 4.5 pct in the sample without slag treatment to 56.4 pct in that treated by slag CS-10La.

Similarly, it was also found that the leaching efficiency of all other impurities slightly increases with the increasing La₂O₃ addition in slag treatment and a final leaching efficiency around 94 pct was reached, as shown in Figure 6.

Simulation Results

Bond Length and Coordination Numbers

The local atomic structure of CaO-La₂O₃-SiO₂ slags was investigated through the pair distribution functions (PDFs). Bond lengths of each studied pairs are obtained according to the distances at first peaks in the g(r) plot shown in Figure 7(a), while the distances at first minimum after the main peak in Figure 7(a) were used for the coordination number determination in the N(r) plot shown in Figure 7(b), which are also set as the cut-off value used for the maximum bonding distance of the atom pair. As shown in Figure 7(a), the Si-O bond is found fairly stable as its g(r) peak is the narrowest. Table V gives the bond length of each atom pair. The cation-anion bond is found less composition dependent, and the average Si-O bond length is around 1.59-1.60 Å, which is slightly lower than the measured value of 1.63 Å by Waseda and Toguri.[51] The bond length of La-O was calculated at around 2.39 Å and slightly longer than the Ca-O bond length of 2.37 Å. However, it still lacks information about the experimental La-O bond length in the CaO-La₂O₃-SiO₂ molten slag. But as reported by Cicconi et al.,[52] the La-O bond length was measured c.a. 2.43 Å in the Na₂O-La₂O₃-SiO₂ glass, which shows consistency with the current study.

Fig. 7

(a) Pair distribution functions of different cation-oxygen and cation-cation pairs in the simulated CS-10 mass pct La₂O₃ slag (b) Integrated coordination number N(r)

Calculated coordination numbers (CNs) of atom pairs are presented in Table VI where the Si-O notation represents the number of O atoms around the central Si atom, taken as an example. It is seen that Si is always bonded with four oxygen atoms known to form the robust [SiO₄] tetrahedral units. As the long plateau presented in Figure 7(b) of the Si-O pair, Si-O bond should be fairly stable, and a high bond strength is expected in all the slag melts. The CN of the Si-Si pair slightly decreases from 2.06 to 1.35 with increasing La₂O₃ addition, reflecting the depolymerization of the Si network. In addition, the increase of La₂O₃ in slags also leads to the increase CN of the Si-La pair but results in the decrease of Ca number around Si. The CN of the La-O is found around 6.5 in all studied slags, which is also in accordance with the experimental value 6.0±0.5 suggested by Cicconi et al.[52] and 6-7 suggested by Angeli et al.[53] The CN of Ca-O is found slightly higher than La-O as 6.8. As shown in Figure 8, the detailed CN population of Ca and La in CS-10 mass pct La₂O₃ slag is presented since no noticeable variations of the Ca-O and La-O coordination were observed. It is seen that the two cations have multiple local environments, and the CNs mostly in the range of 5-8. The most popular oxygen CN of La was 6 and 7, which implies that La-O cluster might mostly be in the form close to distorted octahedron.

Fig. 8

Population analysis of coordination numbers of Ca and La in the simulated CS-10 mass pct La₂O₃ slag

Qⁿ Distribution and Network Connectivity

Slag physical and chemical properties are greatly affected by the Si network structure. A polymerized Si network indicates high slag viscosity and low mass transfer kinetics. In slag chemistry, the polymerization of Si network also links to the increase of SiO₂ activity in general, while a depolymerized Si network facilitates the activity enhancement of modifiers.

The Si network connectivity can be well described by the Qⁿ distribution, which represents the Si tetrahedron that connects n numbers of bridging oxygen, and n varies from 0 to 4. The calculated Qⁿ distribution is plotted in Figure 9. It is seen that Q² unit is the dominant species for the slags used in the refining experiments, which also indicates the [SiO₄] chains and rings are the most popular topology. With the increasing La₂O₃ addition, the Q² specie readily decreases as well as the typical polymerized Qⁿ species (Q⁴, Q³). Accordingly, the fraction of depolymerized units Q¹ and Q⁰ increases in turn with increasing La₂O₃ addition.

Fig. 9

Calculated Qⁿ distribution of studied CaO-La₂O₃-SiO₂ slags with varying La₂O₃ addition

As presented in Figure 10, the depolymerization process of Si network with increasing La₂O₃ addition is also visualized from the snapshots of simulated slags where the long [SiO₄] chains in the initial CaO-SiO₂ slag finally depolymerized to short chains and even in monomers after 30 mass pct La₂O₃ addition. Moreover, nano-segregation of Ca²⁺ can also be observed from the visualized volumetric space of modifiers. As the potential diffusion pathways of modifiers, it can be clearly seen that the volumetric space developed from small pockets to a more channel-connected network, which indicates the significant mobility enhancement of the modifiers. Additionally, with a small amount of La₂O₃ addition, taking the 10 mass pct La₂O₃ addition as an example, a clear tendency can also be observed that La³⁺ cations prefer not to connect with each other and are surrounded by Ca²⁺ cations. This phenomenon also shows good agreement with the experimental evidence offered by Angeli et al.[53] that La prefers homogeneously distributed and requires cations for charge compensation of the excess of non-bridging oxygen in calcium-based borosilicate glass.

Fig. 10

Si network depolymerizes with increasing La₂O₃ addition shown as sectional view of a slice with 6 Å thickness and with the visualized expanding network modifier migration channels of Ca (cyan) and La (pink) (Color figure online)

Diffusion Analysis

The self-diffusion coefficients of O, Si, Ca, and La in the slag melts were calculated from the mean square displacements (MSD) at long times using the following Einstein’s equation:

$$ \begin{array}{*{20}c} {D = \mathop {\lim }\limits_{t \to \infty } \frac{{r^{2} (t)}}{6t} } \\ \end{array}, $$

(5)

where $r^{2} \left( t \right)$ represents the ensemble average MSD, which is the average displacement of atoms over the simulation time t.

As the results plotted in Figure 11, it can be seen that the self-diffusion coefficients of all atoms are positively proportional to the La₂O₃ addition concentration, which indicates that La₂O₃ plays a role of network modification and the slag network structure keeps depolymerizing with increasing La₂O₃ concentration. Additionally, the calculated self-diffusion coefficients of each element also exhibit the following order: D_Ca>D_La>D_O>D_Si. A clear trend in Figure 11 can be seen that D_O and D_Si are adjacent each other, which also reflects that in the CaO-La₂O₃-SiO₂ system, [SiO₄] tetrahedra are the basic structural units and the movement of O atoms cooperatively associates with the movement of Si in the tetrahedra as a whole. Moreover, since Ca shows much higher mobility than La, it may also offer hints that Ca cations are still well dispersed in the slag structure. The lower mobility of La indicates that La cation faces a higher energy barrier to escape its first oxygen coordination shell. The reason is considered to relate to its size effect and the large amount of non-bridging oxygens in the local environment. The detailed structural information will be further presented and discussed in the following section.

Fig. 11

Self-diffusion coefficients of Ca, La, O, and Si in studied CaO-La₂O₃-SiO₂ systems

Discussions

Oxygen Environment and Structural Role of La₂O₃

Slag-refining performance is known affected by the slag optical basicity. From the atomistic viewpoint, the evolution of the oxygen local environment can also reflect the slag composition-property variation. In general, the structural evolution of the slag melt can be described by the variation of different oxygen types such as bridging oxygen (BO), non-bridging oxygen (NBO), and free oxygen (FO). However, this rough classification is still less efficient when treating the mixed network modifiers slag system because it assumes that all network modifiers behave in the same manner. This drawback also holds for the Qⁿ distribution, which assumes all the NBO linkages from different network modifiers are the same. Thus, aiming at deciphering the effect of mixed network modifiers on the oxygen local environment, a novel oxygen classification was defined in the present work.

As presented in Table VII, the classification depends on the cationic environment of the oxygen. A novel species, modified bridging oxygen (mBO), is proposed and defined as the conventional bridging oxygen surrounded by network modifiers. The evidence of the mBO species has also been experimentally provided from the structural analysis of sodo-silicate glass.[54,55] The driving force of the mBO configuration formation may be owing to the tendency of the network modifiers with not high field strength to damp the dipole moment and polarity of the covalent BO. Accordingly, the configurational parameters and dynamic properties of mBO are also supposed to differ from the conventional BO. Thus, the mBO can be treated as another type of BO and also an intermediate state between BO and NBO. Its abundance also reveals the network modifier’s percolation extent in the Si network-polymerized region.

Since Ca and La play different structural roles in slags, it is important to examine the slag structural evolution with La₂O₃ addition. In this work, the calculated conventional and novel distribution of oxygen species are listed in Table VIII, while the flow diagram which represents the distribution of each oxygen species in the 30 mass pct La₂O₃-added CaO-SiO₂ slag is shown in Figure 12.

Fig. 12

Distribution of novel-defined oxygen species in the CaO-La₂O₃-SiO₂ slag system. The width of each flow reflects the relative fraction of the corresponding oxygen types in the slag with 30 mass pct La₂O₃ addition where CaLa-NBO is seen as the most and only popular La-bearing oxygen type

It can be seen from Table VIII that the conventional oxygen classification only reveals limited information that NBO is the dominant oxygen species and its fraction increases with increasing La₂O₃ addition. However, from the distribution of novel-defined oxygen species, it can be seen that most of BO is surrounded by Ca (Ca-mBO), while only a small portion of pure BO exists. More interestingly, it is also found that almost no La-containing mBO detected. By further examining the NBO group, it is seen that the vast majority of La cations appear in the form of LaCa-NBO, which significantly increases from 0.03 to 0.38 mole fraction in the slags from 2 mass pct to 30 mass pct La₂O₃ addition. Accordingly, the Ca-NBO fraction considerably decreases with increasing La₂O₃ addition that from the dominant value 0.63 drops to only 0.35.

The above variation of novel-defined oxygen species demonstrated that Ca²⁺ cations are well dispersed and well percolated in the slag structure in both polymerized and depolymerized regions. However, the La³⁺ cations mainly appear in the depolymerized regions that connect NBOs and require the co-appearance of Ca²⁺ cations to form the LaCa-NBOs. The presence of Ca²⁺ also implies the charge compensation effect due to the excess number of NBOs that results in a more negative local environment around La³⁺. Thus, it is revealed that La plays a dual role in the slag structural evolution. First, La³⁺ behaves as a network modifier and distinctly depolymerizes the slag network. In addition, the high field strength of the trivalent La³⁺ makes it that stabilizes 6-7 NBOs around it and needs the appearance of Ca²⁺ for charge compensation. Nevertheless, the charge compensation effect between two network modifiers is expected much weaker than the typical charge compensation between Ca²⁺ and Al tetrahedra in slags. Thus, the La₂O₃ addition on slag structure exhibits the overall effect of network depolymerization and the modification of the preferential migration pathways of Ca²⁺. If the La₂O₃ content in slag increases much higher, in that case, it is also supposed that the migration of Ca²⁺ could be locally hindered to a slight extent, as it can be seen from Figure 11 that the increment of D_Ca is lower than other species with increasing La₂O₃ addition.

To further understand the difference between Ca²⁺ and La³⁺ in slags, the detailed distribution of oxygen species population is presented in Figure 13 for all studied slags. A clear trend can be observed that the dominant oxygen species shifts from Ca-based oxygen to La-based oxygen, with increasing La₂O₃ addition. Moreover, by looking at the dominant oxygen species in each slag, O-Si(3Ca) is the most popular Ca-based oxygen species, which indicates the Ca-NBO is more preferential to connect with one Si and three Ca. The observed fraction of Ca-based oxygen species follows the following trend:

Fig. 13

Distribution percentage of different oxygen species obtained from MD simulation in the investigated CaO-La₂O₃-SiO₂ slags. The presented oxygen species are with the percentage > 0.05 pct in at least one of the simulated slags where the left side shows the Ca-based oxygen species and the right side shows the La-based oxygen species

$$ {\text{O{-}Si}}\left( { 3 {\text{Ca}}} \right) > {\text{ O{-}Si}}\left( { 2 {\text{Ca}}} \right) > {\text{ O}} - 2 {\text{Si}}\left( {\text{Ca}} \right) > {\text{ O{-}Si}}\left( { 4 {\text{Ca}}} \right) \approx {\text{O}} - 2 {\text{Si}}\left( { 2 {\text{Ca}}} \right). $$

(6)

Additionally, the number of Ca around the Ca-based oxygen also gradually decreases with increases in La₂O₃ content.

The observed most popular La-based oxygen species are O-Si(La2Ca) and O-Si(LaCa), which indicate that the La-based NBO is mostly surrounded by one or two Ca²⁺ ions. Accordingly, the avoidance of the La-O-La structural units is also suggested in low La₂O₃ slags and in accordance with the experimental evidence.[52] Furthermore, the existence of oxygen species with network modifier clustering such as O-Si(3Ca), O-Si(2Ca), and O-Si(La2Ca) is also in good agreement with the percolation theory[56,57] that the network modifiers tend to nano-segregate into percolation channels in partly broken Si network. The migration channels can be also seen in Figure 10.

Concerning the effect of La₂O₃ addition on the slag-refining performance, it is seen that the increasing global slag basicity is achieved by the local oxygen environment variation where more Ca-based oxygen species converted to more basic La-based oxygen species and more reactive sites formed due to the regional high concentration of cations and NBOs. From the kinetics viewpoints, the more depolymerized slag structure also promotes the mass transfer during the refining when the equilibrium is not reached.

Masss Transport of Ca and La and Their Activity

In the slag-refining process, the mass transport not only occurs for the impurities in the metal phase but also takes place for Ca and La in slag that a small portion of them may be transferred into Si melt through the following possible reactions:

$$ \begin{array}{*{20}c} {\underline{\text{Si}} + 2\left( {\text{CaO}} \right) = 2{\underline{\text{Ca}}} + \left( {{\text{SiO}}_{2} } \right)\quad K_{7} \left( {{\text{at}}\,1873 \,{\text{K}}} \right) = 8.4 \times 10^{ - 9} } \\ \end{array}, $$

(7)

$$ \begin{array}{*{20}c} {\underline{\text{Si}} + \frac{2}{3}\left( {\underline{\text{La}}_{2} {\text{O}}_{3} } \right) = \frac{4}{3}{\text{La}} + \left( {{\text{SiO}}_{2} } \right)\quad K_{8} \left( {{\text{at}}\, 1873 \,{\text{K}}} \right) = 4.2 \times 10^{ - 8} } \\ \end{array}. $$

(8)

Since the standard Gibbs energy of formation of the above two reactions is positive, respectively, $\Delta {\text{G}}_{7}^{\circ }$ = 289.6 kJ/mol and $\Delta {\text{G}}_{8}^{\circ }$ = 264.6 kJ/mol, which indicates that the reactions cannot spontaneously happen under standard conditions. The driving force is, thus, attributed to the largely negative deviations of the activities of Ca and La in the Si-rich melt than the ideal solution. According to the measured composition of slag-treated Si-Sn alloys, it is seen that the amount of transferred Ca and La into Si increases with increasing La₂O₃ addition. The reasons are twofold. First, as the obtained self-diffusion coefficients presented in Figure 11, La₂O₃ addition results in more depolymerized slag structure and, therefore, leads to higher diffusivity of Ca and La and better mass transfer kinetics. Second, from the viewpoint of chemical equilibrium, the following relationship can be expressed:

$$ \begin{array}{*{20}c} {x_{\text{Ca}} = \left[ {\frac{{a_{\text{Si}} a_{\text{CaO}}^{2} }}{{a_{{{\text{SiO}}_{2} }} }}\exp \left( {\frac{{ - \Delta {\text{G}}_{7}^{\circ } }}{\text{RT}}} \right)} \right]^{{\frac{1}{2}}} /\gamma_{\text{Ca}} } \\ \end{array}, $$

(9)

$$ \begin{array}{*{20}c} {x_{\text{La}} = \left[ {\frac{{a_{\text{Si}} a_{{{\text{La}}_{2} {\text{O}}_{3} }}^{{\frac{2}{3}}} }}{{a_{{{\text{SiO}}_{2} }} }}\exp \left( {\frac{{ - \Delta {\text{G}}_{8}^{\circ } }}{\text{RT}}} \right)} \right]^{{\frac{3}{4}}} /\gamma_{\text{La}} } \\ \end{array}. $$

(10)

Assume the variation of $\gamma_{Ca}$, $\gamma_{La}$, and $a_{Si}$, is insignificant due to the small portion of metals transferred, and the exponential term is known constant, it is seen that the concentration of Ca and La in Si melt increases with decreasing $a_{{{\text{SiO}}_{2} }}$ and increasing $a_{CaO}$, $a_{{La_{2} O_{3} }}$.

The above discussion is also supported by the calculated chemical activity and activity coefficient of components in the Si-Sn alloys using FactSage 8.0 with FTlite database. As listed in Table IX, large negative deviation of $a_{Ca}$ and $a_{La}$ can be observed from the distinctly small activity coefficient of Ca and La and further supports the above discussion. Moreover, the activity coefficients of Ca and La in dilute solutions can be estimated as ${{\gamma }}_{Ca}^{\circ } = 3.55 \times 10^{ - 4}$ and ${{\gamma }}_{La}^{\circ } = 1.10 \times 10^{ - 5}$ at 1873 K (1600 °C). It is seen that even with small portion of Sn addition, the obtained activity coefficient of Ca value $ln{{\gamma }}_{Ca}^{\circ } = - 7.94$ is still comparable but smaller than the measured values $ln{{\gamma }}_{Ca}^{\circ } = - 6.99$ in the most recent work by Jakobsson and Tangstad[22] from the equilibrium analysis between CaO-SiO₂ slag and Si melt. The calculated $a_{\text{Si}}$ values are closed to the Si molar fraction and, therefore, approximately follow the Raoultian behavior in the studied composition range, while the activity of Sn is shown largely positive deviation, which is in good agreement with the results in the literature.[58] Additionally, the calculated ${{\gamma }}_{B}^{\circ } = 3.64$ in CaO-SiO₂ slag-treated Si-rich melt is in accordance with the value ${{\gamma }}_{B}^{\circ } = 3.84 \pm 1.63$ at 1873 K (1600 °C) measured by Yoshikawa and Morita[59] but seems to decrease with increasing Ca and La contents in the melt.

Slag Chemistry and the Effect of La₂O₃ on B Removal

The thermodynamic assessment of the CaO-La₂O₃-SiO₂ system is barely reported. Even though the short holding time in this work may be insufficient to ensure the equilibrium state, the estimation of chemical activity of slag components still provides valuable information for the effect of La₂O₃ on slag chemistry. Thus, the activity of CaO and La₂O₃ is calculated as follows:

$$ \begin{array}{*{20}c} {a_{\text{CaO}} = \left[ {\frac{{a_{{{\text{SiO}}_{2} }} a_{\text{Ca}}^{2} }}{{a_{\text{Si}} { \exp }\left( {\frac{{ - \Delta {{\text{G}}_{7}^{\circ }} }}{RT}} \right)}}} \right]^{{\frac{1}{2}}} } \\ \end{array}, $$

(11)

$$ \begin{array}{*{20}c} {a_{{{\text{La}}_{2} {\text{O}}_{3} }} = \left[ {\frac{{a_{{{\text{SiO}}_{2} }} a_{\text{La}}^{{\frac{4}{3}}} }}{{a_{\text{Si}} { \exp }\left( {\frac{{ - \Delta {{\text{G}}_{8}^{\circ }} }}{RT}} \right)}}} \right]^{{\frac{3}{2}}} } \\ \end{array}. $$

(12)

Regarding to the oxidation of dissolved B and P in Si melt, the following reactions may happen:

$$ \begin{array}{*{20}c} {2{\underline{\text{B}}} + \frac{3}{2}\left( {{\text{SiO}}_{2} } \right) = \left( {{\text{B}}_{2} {\text{O}}_{3} } \right) + \frac{3}{2}{\text{Si}} \,K_{13}\quad \left( {{\text{at}}\, 1873\quad \,{\text{K}}} \right) = 1.9 \times 10^{ - 1} } \\ \end{array}, $$

(13)

$$ \begin{array}{*{20}c} {4{\underline{\text{P}}} + 5\left( {{\text{SiO}}_{2} } \right) = 2\left( {{\text{P}}_{2} {\text{O}}_{5} } \right) + 5{\text{Si}} \,K_{14}\quad \left( {{\text{at}} \,1873\quad \, {\text{K}}} \right) = 3.7 \times 10^{ - 43} } \\ \end{array}. $$

(14)

Therefore, the activity of $a_{{{\text{B}}_{2} {\text{O}}_{3} }}$ and $a_{{{\text{P}}_{2} {\text{O}}_{5} }}$ could be estimated as follows:

$$ \begin{array}{*{20}c} {a_{{{\text{B}}_{2} {\text{O}}_{3} }} = \frac{{a_{{{\text{SiO}}_{2} }}^{{\frac{3}{2}}} a_{\text{B}}^{2} }}{{a_{\text{Si}}^{{\frac{3}{2}}} }}K_{13} } \\ \end{array}, $$

(15)

$$ \begin{array}{*{20}c} {a_{{{\text{P}}_{2} {\text{O}}_{5} }} = \left[ {\frac{{a_{{{\text{SiO}}_{2} }}^{5} a_{\text{P}}^{4} }}{{a_{\text{Si}}^{5} }}K_{14} } \right]^{{\frac{1}{2}}} } \\ \end{array}. $$

(16)

The estimated thermodynamic values of each component are listed in Table X where the $a_{{{\text{SiO}}_{2} }}$ is calculated based on the results obtained by Jakobsson and Tangstad[22] in the binary CaO-SiO₂ system and referring the optical basicity of the studied slags to equivalent $x_{{{\text{SiO}}_{2} }}$ value, respectively, 0.50, 0.49, and 0.46 for the studied three slags. Wu and Wang[60] equilibrated CaO-La₂O₃-SiO₂ slags with Sn melt at 1873 K (1600 °C) under CO atmosphere, and the measured results show that the activities of CaO and La₂O₃ increase with increasing La₂O₃, and the values of $a_{CaO}$ and $a_{{La_{2} O_{3} }}$in the 47.8 mol pct CaO- 50.3 pct SiO₂- 1.9 pct La₂O₃ slag are obtained as 0.0055 and $8.7 \times 10^{ - 7}$, which is considered to be referenced to the slag CS-2La due to the similar slag composition. It is seen that the estimated values $a_{CaO} = 0.0027$ and $a_{{La_{2} O_{3} }} = 4.7 \times 10^{ - 8}$ are lower than the measured results by Wu and Wang.[60] In addition, the estimated $a_{CaO}$ is seen slightly lower than the values reported by different researchers that were summarized by Jakobsson and Tangstad,[22] which falls in the range from 0.004 to 0.008. The main reason for the underestimation should be attributed to the unachieved equilibrium state of the slag-metal system due to the short slag-refining time in this work. On the other hand, the estimation also suggests that under equilibrium state, the Ca concentration in Si melt should be approximately two times more than the current value. The estimated values also show the decreases of activity coefficient of B₂O₃ after La₂O₃ addition, which suggests that the La₂O₃ addition benefits the B removal and further stabilizes B in slag. Moreover, by treating B₂O₃ as BO_1.5, the following linear relationship can be obtained:

$$ \begin{array}{*{20}c} {{{\gamma }}_{{{\text{B}}1.5}}^{\circ } = 0.12{{\gamma }}_{{{\text{SiO}}_{2} }} } \\ \end{array}. $$

(17)

The ratio is, however, lower than the value 0.41 reported by Jakobsson from the equilibrated slag refining of Si using CaO-SiO₂ slag. Thus, it is expected that the L_B value obtained in the present work might be even higher under full equilibrium. The reason for the improved B removal after La₂O₃ addition is manifold but complex. First, it has been reported that L_B is positively related to the slag optical basicity. The high optical basicity of La₂O₃ (1.18) is, therefore, preferred. Furthermore, as the simulation results suggested, the addition of La₂O₃ results in more reactive NBOs. The dominant Q² species also favors incorporating B into the Si network. Additionally, the high field strength of La³⁺ promotes the conversion of four-coordinated B to three-coordinated,[61,62] which is also associated with the decrease of the activity coefficient of B₂O₃ and B stabilization in slag.[36] On the contrary, if too much La₂O₃ is added, the negative local environment of La³⁺ may also result in competition with B for the charge compensation, and much more La may also diffuse into the Si phase, which further, in turn, stabilizes more B in the Si phase. According to the obtained L_B results, not only the overall effect of La₂O₃ addition is distinctly positive for B removal, but it is also seen that the increment of L_B narrows with more La₂O₃ addition.

Effect of Sn Addition on Impurity Distribution

Slag refining is known as a complicated function of slag composition, silicon melt composition, temperature, time, and also impurity type. In order to further discuss the alloying effect on slag-refining performance, for convenience, the molar ratio-based distribution ratio l is firstly adopted for model derivation and then converted to mass fraction-based L. Therefore, for the slag-refining extraction of arbitrary impurity (M) with valence v, we have

$$ \begin{array}{*{20}c} {l_{M} = \frac{{x_{{{\text{MO}}_{{\frac{v}{2}}} }}^{\text{slag}} }}{{x_{\text{M}}^{\text{Si\, melt}} }} } \\ \end{array}. $$

(18)

In slag refining, the following reaction exists:

$$ \begin{array}{*{20}c} {\underline{\text{M}} + \frac{v}{4}{\text{SiO}}_{2} = \frac{v}{4}{\underline{\text{Si}}} + {\text{MO}}_{{\frac{v}{2}}} } \\ \end{array}. $$

(19)

Thus, the equilibrium constant of reaction (19) can be calculated as follows:

$$ \begin{array}{*{20}c} {K_{20} = \frac{{\left( {a_{\text{Si}}^{\text{Si\, melt}} } \right)^{{\frac{v}{4}}} }}{{\left( {a_{{{\text{SiO}}_{2} }}^{\text{slag}} } \right)^{{\frac{v}{4}}} }} \cdot \frac{{a_{{{\text{MO}}_{{\frac{v}{2}}} }}^{\text{slag}} }}{{a_{\text{M}}^{\text{Si\, melt}} }} = \frac{{\left( {a_{\text{Si}}^{\text{Si\, melt}} } \right)^{{\frac{v}{4}}} }}{{\left( {a_{{{\text{SiO}}_{2} }}^{\text{slag}} } \right)^{{\frac{v}{4}}} }} \cdot \frac{{x_{{{\text{MO}}_{{\frac{v}{2}}} }}^{\text{slag}} }}{{x_{\text{M}}^{\text{Si\, melt}} }} \cdot \frac{{\gamma_{{MO_{{\frac{v}{2}}} }}^{\text{slag}} }}{{\gamma_{\text{M}}^{\text{Si\, melt}} }} } \\ \end{array}. $$

(20)

After rearrangement,

$$ \begin{array}{*{20}c} {\ln \left( {l_{M} } \right) = \ln \left( {K_{20} } \right) + \ln \left( {\frac{{\left( {a_{{{\text{SiO}}_{2} }}^{\text{slag}} } \right)^{{\frac{v}{4}}} }}{{\gamma_{{MO_{{\frac{v}{2}}} }}^{\text{slag}} }}} \right) + \ln \left( {\frac{{\gamma_{\text{M}}^{\text{Si\, melt}} }}{{\left( {a_{\text{Si}}^{\text{Si\, melt}} } \right)^{{\frac{v}{4}}} }}} \right) } \\ \end{array}. $$

(21)

Assume the introduction of alloying element A and the transferred small amount impurities have no significant effects on slag chemistry, thus, the reaction constant and slag related term in Eq. [21] can be compensated and the variation of $ln \left( {l_{M} } \right)$ can be expressed as follows:

$$ \begin{array}{*{20}c} {\Delta \ln \left( {l_{M} } \right) = \ln \left( {\frac{{l_{M}^{*} }}{{l_{M}^{0} }}} \right) = \ln \left( {\frac{{\gamma_{\text{M}}^{*\text{Si - A\, melt}} }}{{\left( {a_{\text{Si}}^{*\text{Si - A\, melt}} } \right)^{{\frac{v}{4}}} }}} \right) - \ln \left( {\frac{{\gamma_{\text{M}}^{\text{Si\, melt}} }}{{\left( {a_{\text{Si}}^{\text{Si\, melt}} } \right)^{{\frac{v}{4}}} }}} \right) } \\ \end{array}, $$

(22)

where $a_{\text{Si}}^{*{{\text{Si}} - {\text{A\, melt}}}}$ and $\gamma_{\text{M}}^{*{S{\text{i}} - {\text{A\, melt}}}}$ denote, respectively, the chemical activity and activity coefficient of impurity M in Si-A melt. $l_{M}^{*}$ and $l_{M}^{0}$ represent the molar ratio-based distribution ratio of the Si-A alloy and Si without alloying, respectively.

Rearrange Eq. [22], it yields

$$ \begin{array}{*{20}c} {\Delta \ln \left( {l_{{M}} } \right) = \ln \left[ {\left( {\frac{{\gamma_{\text{M}}^{*\text{Si - A\, melt}} }}{{\gamma_{\text{M}}^{\text{Si\, melt}} }}} \right)\left( {\frac{{a_{\text{Si}}^{\text{Si\, melt}} }}{{a_{\text{Si}}^{*\text{Si - A\, melt}} }}} \right)^{{\frac{v}{4}}} } \right] } \\ \end{array}. $$

(23)

As the impurity content in the metal phase is usually negligible, the following relationship should exist $\gamma_{\text{M}}^{\text{Si\, melt}} = \gamma_{\text{M}}^{0\,{{\text{Si}}\, {\text{melt}}}}$. According to the Bale-Pelton formalism,[63] we have

$$ \begin{array}{*{20}c} {\ln \gamma_{\text{M}}^{{*{\text{Si}} - {\text{A\, melt}}}} = \ln \gamma_{\text{M}}^{{0\,{\text{Si\, melt}}}} + \ln \gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{A\, melt}}}} + \varepsilon_{\text{M}}^{\text{M}} x_{\text{M}}^{{{\text{Si}} - {\text{A\, melt}}}} + \varepsilon_{\text{A}}^{\text{M}} x_{\text{A}}^{{{\text{Si}} - {\text{A\, melt}}}} } \\ \end{array}, $$

(24)

where $\gamma_{\text{M}}^{0\,{{\text{Si\, melt}}}}$ represents the activity coefficient of impurity M at infinite dilution in the Si melt, and $\varepsilon$ denotes the first-order interaction coefficient. Inserting Eq. [24] into Eq. [23], we obtain

$$ \begin{array}{*{20}c} {\Delta \ln \left( {l_{M} } \right) = \ln \left( {\frac{{l_{M}^{*} }}{{l_{M}^{0} }}} \right) = \left( {{\text{ln }}\gamma_{\text{Si}}^{*{{\text{Si}} - {\text{A\, melt}}}} + \varepsilon_{\text{M}}^{\text{M}} x_{\text{M}}^{*{{\text{Si}} - {\text{A\, melt}}}} + \varepsilon_{\text{A}}^{\text{M}} x_{\text{A}}^{*{{\text{Si}} - {\text{A\, melt}}}} } \right) + \ln \left( {\frac{{a_{\text{Si}}^{\text{Si\, melt}} }}{{a_{\text{Si}}^{*{{\text{Si}} - {\text{A\, melt}}}} }}} \right)^{{\frac{v}{4}}} } \\ \end{array} $$

(25)

Due to the insignificant amount of impurity M in Si melt, the term $\varepsilon_{\text{M}}^{\text{M}} x_{\text{M}}^{*{{\text{Si}} - {\text{A\, melt}}}}$ can be ignored, and $a_{\text{Si}}^{\text{Si\, melt}}$ equals to unit. Thus, Eq. [25] is further simplified as follows:

$$ \begin{array}{*{20}c} {\Delta \ln \left( {l_{M} } \right) = \ln \left( {\frac{{l_{M}^{*} }}{{l_{M}^{0} }}} \right) = \left( {{\text{ln }}\gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{A\, melt}}}} + \varepsilon_{\text{A}}^{\text{M}} x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right) + \ln \left( {\frac{1}{{x_{\text{Si}}^{{ * {\text{Si}} - {\text{A\, melt}}}} \gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{A\, melt}}}} }}} \right)^{{\frac{v}{4}}} } \\ \end{array}. $$

(26)

And because $x_{\text{Si}}^{*{{\text{Si}} - {\text{A\, melt}}}} = 1 - x_{\text{A}}^{*{{\text{Si}} - {\text{A\, melt}}}}$, Eq. [27] is obtained:

$$ \begin{array}{*{20}c} {\ln \left( {l_{M} } \right) = \ln \left( {\frac{{l_{M}^{*} }}{{l_{M}^{0} }}} \right) = \left( {\varepsilon_{\text{A}}^{\text{M}} x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right) + \ln \left[ {\left( { \gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right)^{{\frac{4 - v}{4}}} \left( {\frac{1}{{1 - x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} }}} \right)^{{\frac{v}{4}}} } \right] } \\ \end{array}. $$

(27)

Thus, the alloying effect on molar fraction-based distribution ratio can be expressed as follows:

$$ \begin{array}{*{20}c} {\frac{{l_{M}^{*} }}{{l_{M}^{0} }} = \left( {\gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right)^{{\frac{4 - v}{4}}} \left( {\frac{1}{{1 - x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} }}} \right)^{{\frac{v}{4}}} \exp \left( {\varepsilon_{\text{A}}^{\text{M}} x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right) } \\ \end{array}. $$

(28)

In order to obtain the relationship with $L_{M}$, the conversion factor $k_{x \to w}$ for all the elements in the system is introduced and written as below[64]:

$$ \begin{array}{*{20}c} {L_{M} = l_{M} \cdot k_{x \to w} = l_{M} \cdot \frac{{x_{\text{Si}} M_{\text{Si}} + \sum x_{\text{Me}} M_{\text{Me}} }}{{x_{{{\text{SiO}}_{2} }} M_{{{\text{SiO}}_{2} }} + \sum x_{{{\text{MeO}}_{x} }} M_{{{\text{MeO}}_{x} }} }} } \\ \end{array}, $$

(29)

where the element Me and its oxide MeO_x indicate the other elements in Si and slag, and $M_{\text{Me}}$ and $M_{{{\text{MeO}}_{x} }}$ indicate their corresponding molar mass.

$$ \begin{array}{*{20}c} {\frac{{L_{M}^{*} }}{{L_{M}^{0} }} = \frac{{l_{M}^{*} }}{{l_{M}^{0} }} \cdot \frac{{x_{\text{Si}}^{*{{\text{Si}} - {\text{A\, melt}}}} M_{\text{Si}} + \sum x_{\text{Me}}^{*{{\text{Si}} - {\text{A\, melt}}}} M_{\text{Me}} }}{{M_{\text{Si}} }} } \\ \end{array}. $$

(30)

For the Si-A binary system with insignificant quantity of impurities, introducing $x_{\text{Si}}^{*{{\text{Si}} - {\text{A\, melt}}}} = 1 - x_{\text{A}}^{*{{\text{Si}} - {\text{A\, melt}}}}$, we have

$$ \begin{array}{*{20}c} {\frac{{L_{M}^{*} }}{{L_{M}^{0} }} = \frac{{l_{M}^{*} }}{{l_{M}^{0} }} \cdot \left( {1 + \frac{{M_{\text{A}} - M_{\text{Si}} }}{{M_{\text{Si}} }}x_{\text{A}}^{*{{\text{Si}} - {\text{A\, melt}}}} } \right) } \\ \end{array}. $$

(31)

Finally,

$$ \begin{array}{*{20}c} {\frac{{L_{{M}}^{*} }}{{L_{{M}}^{0} }} = \left( {\gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right)^{{\frac{4 - v}{4}}} \left( {\frac{1}{{1 - x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} }}} \right)^{{\frac{v}{4}}} exp\left( {\varepsilon_{\text{A}}^{\text{M}} x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right) \cdot \left( {1 + \frac{{M_{\text{A}} - M_{\text{Si}} }}{{M_{\text{Si}} }}x_{\text{A}}^{{ * {\text{Si}} - {\text{A\, melt}}}} } \right) } \\ \end{array}. $$

(32)

It can be seen that slag refining of Si alloy is affected by multiple factors, respectively, concentration of alloying element $x_{\text{A}}^{{{\text{Si}} - {\text{A\, melt}}}}$, activity coefficient of Si, $\gamma_{\text{Si}}^{*{{\text{Si}} - {\text{A}}\, {\text{melt}}}}$, valence of the impurity v, the interaction coefficient of alloying element to the target impurity $\varepsilon_{\text{A}}^{\text{M}}$, and molar mass of the alloying element $M_{\text{A}}$. Further to say, if one wants to improve the L_M value, the alloying element with high and positive interaction coefficient values $\varepsilon_{\text{A}}^{\text{M}}$ is preferred. In addition, with a positive $\varepsilon_{\text{A}}^{\text{M}}$, it can be seen that the alloying concentration should play a strongly positive role as it appears in both the term of the power function and exponential function. According to the mass fraction conversion term, it is seen that if the alloying metal is heavier than Si, i.e., $M_{\text{A}} > M_{\text{Si}}$, the alloying process could magnify the L_M physically as well by diluting the impurity mass fraction. Moreover, the valence of impurity and activity coefficient of Si is also influential to determine the alloying efficiency. Thus, considering the impurity of B and P, and by assigning Sn as the alloying element, we can obtain

$$ \begin{array}{*{20}c} {\frac{{L_{{B}}^{*} }}{{L_{{B}}^{0} }} = \left( {\gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} } \right)^{{\frac{1}{4}}} \left( {\frac{1}{{1 - x_{\text{Sn}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} }}} \right)^{{\frac{3}{4}}} \exp \left( {\varepsilon_{\text{Sn}}^{\text{B}} x_{\text{Sn}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} } \right) \cdot \left( {1 + 3.23x_{\text{Sn}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} } \right) } \\ \end{array}, $$

(33)

$$ \begin{array}{*{20}c} {\frac{{L_{P}^{*} }}{{L_{P}^{0} }} = \left( {\frac{1}{{\gamma_{\text{Si}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} }}} \right)^{{\frac{1}{4}}} \left( {\frac{1}{{1 - x_{\text{Sn}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} }}} \right)^{{\frac{5}{4}}} \exp \left( {\varepsilon_{\text{Sn}}^{\text{P}} x_{\text{Sn}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} } \right) \cdot \left( {1 + 3.23x_{\text{Sn}}^{{ * {\text{Si}} - {\text{Sn\, melt}}}} } \right) } \\ \end{array}. $$

(34)

By employing the thermodynamic data of Si-Sn system calculated by FactSage 8.0 using FTlite database, Figure 14 is obtained to further access the obtained relationship. As shown in Figure 14(a), a strongly positive deviation from ideal solution can be seen in the Si-Sn system. According to the Si activity coefficient term shown in Eqs. [34] and [35], this trend is in favor of B separation. Moreover, by knowing $\gamma_{\text{Si}}^{*{{\text{Si}} - {\text{Sn\, melt}}}}$, the interaction coefficient $\varepsilon_{Sn}^{\text{B}}$ can also be estimated. Thus, as presented in Figure 14(b), the value of $\varepsilon_{Sn}^{\text{B}}$ is roughly estimated by merging the reported data from the literature to evaluate the obtained model performance. In the estimation, the slag-refining results of Si-Sn alloys from Ma et al.[40] at 1673 K (1400 °C) was adopted for the $L_{B}^{*}$, while the corresponding $L_{B}^{0}$ at the same condition was set as 1.2 based on the results from Teixeira and Morita[24] using the similar slag composition and the $\gamma_{\text{Si}}^{*{{\text{Si}} - {\text{Sn\, melt}}}}$. It can be seen that the predicted trend is in good agreement with the experimental results, and the value of $\varepsilon_{Sn}^{\text{B}}$ at 1673 K (1400 °C) can be estimated roughly around 4.

Fig. 14

(a) Calculated activity of Si and Sn at 1873 K (1600 °C) by FactSage 8.0 using FTlite database, (b) Model evaluation by estimating of $\varepsilon_{Sn}^{\text{B}}$ value from literature data[24,40] at 1673 K (1400 °C), (c) Effect of Sn concentration and interaction coefficient on B distribution at 1873 K (1600 °C), (d) P distribution against varying Sn concentration and interaction coefficient values at 1873 K (1600 °C)

To further reveal the critical role of the interaction between impurity and alloying element, Figures 14(c) and (d) is presented with varying assumed interaction coefficient values. It is seen that the interaction coefficient is a very sensitive factor for $L_{B}^{*}$ and $L_{P}^{*}$, and their values remarkably increase with increasing Sn concentration for the assumed positive $\varepsilon_{Sn}^{B}$ values. However, it is seen that even though there is no assumed interaction B and Sn, the $L_{B}^{*}$ and $L_{P}^{*}$ can still slightly increase. The reason is attributed to the power function term and the heavy molar mass of Sn.

Acid Leaching of Slag-Treated Alloy

As can be seen from Table IV, the alloy composition was modified after slag refining. The increasing La₂O₃ addition results in more depolymerized slag structure and better mass transfer conditions; thus, more Ca and La diffused into the metal phase. Consequently, alloy microstructure was modified as well with the formation of Ca-Sn and Ca-La-Sn precipitates and the impurity segregation of B and P during the alloy solidification process should also be affected.

As Figure 6 presents, the leaching of slag-treated samples exhibited higher impurity removal efficiency than the direct leaching of the Si-Sn alloy without slag treatment. The reasons are twofold. First, the initial Si-Sn alloy was obtained by casting, and the slag-treated alloys underwent much slower cooling; thus, the segregation of B and P is promoted by the lower cooling rate.[47] Second, and more importantly, the increasing Ca and La concentration in the Si melt promotes the impurity segregation. It is also seen that with increasing Ca and La concentration in the alloy, P removal efficiency significantly increases. The reason is explained by its decreasing segregation coefficient due to the alloy composition. Given the Si-Me metallic system as an example, the variation of P segregation coefficient can be expressed as follows[8,47,65]:

$$ \begin{array}{*{20}c} {k_{\text{P}}^{{{\text{Si}} - {\text{Me}}}} = k_{\text{P}}^{\text{Si}} \exp \left( {\frac{{\varepsilon_{\text{Me}}^{\text{P}} x_{\text{Me}} }}{{1 - f_{s} }}} \right) } \\ \end{array}, $$

(35)

where $k_{\text{P}}^{\text{Si}}$ is the P segregation coefficient in pure Si, which equals 0.35, and $x_{\text{Me}}$ denotes the concentration of alloying elements in alloy liquid, and $f_{s}$ represents the solid fraction of primary Si.

It can be seen from Eq. [35] that the increasing concentration of element with negative $\varepsilon_{\text{Me}}^{\text{P}}$ value can decrease the P segregation coefficient and, therefore, promote the impurity removal in acid leaching. The value of $\varepsilon_{Ca}^{\text{P}} = - 14.6$ measured by Shimpo et al.[65] at 1723 K (1450 °C)[65] well supports the above explanation and the reported low Gibbs energy of formation of the lanthanide monophosphides[66] also implies the promoted P segregation in the slag-treated alloy. Thus, it is expected that the increasing slag basicity results in higher Ca and La contents in the metal phase, which further promotes the P segregation and benefits its removal in acid leaching. As shown in Figure 5, B removal is also improved after slag refining but seems not sensitive to slag composition. The reasons may be owing to the intrinsic high segregation coefficient (k_B=0.8) limits the enhancement. Simultaneously, the measurement error at several ppmw levels and the potential formation of boron-oxygen complexes due to slag refining may also affect the obtained results.

Conclusion

In this work, effects of La₂O₃ addition in CaO-SiO₂ slag on the slag-refining performance with Si-10 mass pct Sn alloy at 1873 K (1600 °C) were investigated with the main following conclusions:

• 1. Enhanced B and P removal was found in the slag refining with increasing La₂O₃ addition. The L_B values readily increased from 2.93 in binary CaO-SiO₂ slag system to 3.33 and 3.65 with 2 mass pct and 10 mass pct La₂O₃ addition. The L_P values slightly increase from 0.29 to 0.42 with increasing La₂O₃ in slag.

• 2. The acid-leaching experiments revealed around 30 pct B removal from the alloys (after slag treatment), and the leaching efficiency of P significantly improved from 4.5 pct to 56.4 pct. The enhancement is mainly attributed to the increased Ca and La contents in the Si-Sn alloy after slag refining and their behavior upon the alloy solidification.

• 3. The oxygen local environment and structural role of La₂O₃ in CaO-La₂O₃-SiO₂ slags were revealed by a novel oxygen classification method for the study of mixed network modifiers effect. It was found that La cations play a role of typical network modifier and with a coordination number around 6.5. Differ from Ca cations, La cation mainly appears in the depolymerized region and connects with NBO and requires the co-appearance of Ca for a weak charge compensation.

• 4. A thermodynamic model was derived to understand the slag refining of Si binary alloys. It was found that the slag-refining performance affected by multiple factors, respectively, concentration of alloying element, activity coefficient of Si, valence of the impurity, and the interaction coefficient of alloying element to the target impurity, where positive interaction coefficient and high alloying concentration are preferred for improved impurity removal.