Determination of Gibbs Free Energy of Formation of MnV₂O₄ Solid Solution at 1823 K (1550 °C)

Abstract

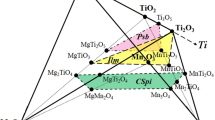
The Gibbs free energy of formation of MnV₂O₄ solid solution saturated with either MnO or V₂O₃ was experimentally determined at 1823 K (1550 °C) by employing a chemical equilibrium technique. The MnV₂O₄ solid solution mixed with MnO or V₂O₃ was brought to equilibrium with either liquid Fe or liquid Cu to measure equilibrium compositions of the liquid metal. Using the available thermodynamic parameters such as Wagner’s interaction parameter for liquid Fe or Gibbs free energy of liquid solution composed of Cu-Mn-V-O, the Gibbs free energy of formation of the MnV₂O₄ solid solution from constituent oxides (MnO and V₂O₃) was then determined to be: MnO(s) + V₂O₃(s) = MnV₂O₄(MnO-satd.): $\Updelta g^\circ_{{\rm f,MnV}_{2}{\rm O}_{4}}$ = −31.4 ± 2 (kJ/mol); MnO(s) + V₂O₃(s) = MnV₂O₄(V₂O₃-satd.): $\Updelta g^\circ_{{\rm f,MnV}_{2}{\rm O}_{4}}$ = −37.8 ± 2 (kJ/mol). The $\Updelta g^\circ_{{\rm f,MnV}_{2}{\rm O}_{4}}$ values were independent of the oxygen partial pressure within the range from 2.0 × 10⁻¹² to 6.3 × 10⁻¹¹, employed in the current study.

Appendix

A. Preparation of MnV₂O₄ Crucibles Saturated by Either MnO or V₂O₃

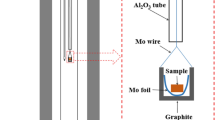
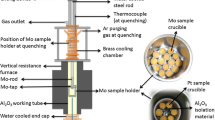
MnO (99.9 pct purity, Kojundo, Chemical Co., Japan) and V₂O₃ reduced from V₂O₅ (99.0 pct purity, Daejung Chemicals Ltd., Gyeongg-Do, Korea) by H₂ gas in the current study, both in powder form, were mixed to fabricate MnV₂O₄ crucible saturated by MnO (0.79 : 0.21 in mass ratio) or by V₂O₃ (0.19 : 0.81 in mass ratio), respectively. Fifty grams of each mixture was compressed into a crucible shape [outer diameter (OD): 30 mm, inner diameter (ID): 20 mm, height (H): 35 mm] by a hydraulic press at pressure around 0.15 GPa as shown in Figure A1. This crucible was put into a MgO holder (OD: 52 mm, ID: 40 mm, H: 70 mm) and placed in the furnace for 24 hours under a H₂/CO₂ gas mixture (P_{H 2}/P_{CO 2} = 9) to get MnV₂O₄ in equilibrium with MnO or V₂O₃, and to sinter the MnV₂O₄ crucible as well. After equilibration and sintering, rapid quenching into cold water was followed. An x-ray diffraction (XRD) analysis for each MnV₂O₄ crucible was conducted to confirm that the MnV₂O₄ coexisted with MnO or V₂O₃ as shown in Figure A2.

Fig. A1

Photographs of a MnV₂O₄ crucible saturated with MnO (Online version in color)

Fig. A2

X-ray diffraction patterns of MnV₂O₄ crucibles in comparison with standard peaks of MnO, V₂O₃, and MnV₂O₄

B. Contamination of MnV₂O₄ Phase in Contact with the Liquid Fe Under H₂/CO₂ Gas Mixture

At first, a H₂/CO₂ gas mixture (P_{H 2}/P_{CO 2} = 9) was used to control the oxygen partial pressure and to maintain the stable oxide phases (MnO and MnV₂O₄ saturated with MnO) when liquid Fe was used as the metal solvent. However, there was a considerable Fe dissolution into the oxide phases as shown in Figure B1(a). The proportions of Fe-oxide in MnO and MnV₂O₄ solid solution were found to be considerably high by EPMA quantitative analysis (Fe:Mn = 1:2 in atomic ratio). Therefore, activity of MnV₂O₄ spinel phase could not be assumed to be unity. To avoid the contamination by Fe-oxide, purified Ar atmosphere was introduced instead of the H₂/CO₂ gas mixture, and the EPMA mapping analysis for this sample is shown in Figure B1(b). As can be seen in the figure, Fe contamination into the oxide phases decreased remarkably. An EPMA quantitative analysis indicated that the amount of Fe dissolved into those phases was less than 0.6 mass pct which was considered to be small enough to ignore the effect of Fe-oxide on the activity of MnV₂O₄ spinel solid solution.

Fig. B1

EPMA mapping analysis of the oxide phases in the MnV₂O₄ crucible saturated with MnO under different metals and gas conditions (Online version in color)

Apart from this, to maintain the H₂/CO₂ gas mixture condition but to avoid the contamination by oxidation of liquid Fe, the use of liquid Cu in place of Fe was attempted. Although the experimental condition remained the same (MnV₂O₄ saturated with MnO and H₂/CO₂ gas condition), the crucible samples after 24 hours-equilibrium experiment with the liquid Cu was subjected to an EPMA mapping analysis for an examination of the oxide phases in the crucible. From Figure B1(c), the oxide phases in equilibrium with the liquid Cu and H₂/CO₂ atmosphere were not contaminated by Cu-oxide because of the relatively weak oxygen affinity of Cu compared with that of Fe. Therefore, eventually in the current study, two experimental conditions were used to measure the Gibbs free energy of formation of MnV₂O₄ saturated with either MnO or V₂O₃:

• (a) Liquid Fe + MnV₂O₄ + purified Ar condition

• (b) Liquid Cu + MnV₂O₄ + H₂/CO₂ condition

C. Gibbs Free Energy of Formation of Non-stoichiometric MnV₂O₄

In Section III–B, the $\Updelta g^\circ_{{\rm f,MnV}_{2}{\rm O}_{4}}$ values were determined based on Reaction [1], which assumes one mole of stoichiometric MnV₂O₄ spinel formation from one mole of MnO and V₂O₃. However, the MnV₂O₄ phases in equilibrium with liquid metals were not stoichiometric under the experimental conditions of the current study. For nonstoichiometric MnV₂O₄ formation, Reactions [1], [2], and [11] should be modified as described below:

$$ x\hbox{MnO(s)} + \frac{y}{2}\hbox{V}_{2}\hbox{O}_{3}(\hbox{s}) = \hbox{Mn}_x\hbox{V}_y\hbox{O}_{x+1.5y}(\rm s) $$

(C1)

$$ x{\underline{\rm Mn}} + y{\underline{\rm V}} + (x+1.5y){\underline{\rm O}} = \hbox{Mn}_x\hbox{V}_y\hbox{O}_{x+1.5y}\hbox{(s)} \quad (\hbox{in liquid Fe}) $$

(C2)

$$ x\hbox{Mn(l)} + y\hbox{V(l)} + \frac{x+1.5y}{2} {\hbox{O}_{2}(\hbox{g})} = \hbox{Mn}_x\hbox{V}_y\hbox{O}_{x+1.5y}\hbox{(s)} \quad (\hbox{in liquid Cu}) $$

(C3)

where x and y are the number of moles of Mn and V participated in non-stochiometric MnV₂O₄ formation, repectively. Here, the stoichiometric coefficient of dissolved oxygen in Eq. [C2] or that of oxygen gas in Eq. [C3] were determined with the assumption that only divalent Mn and trivalent V are considered to form a nonstoichiometric MnV₂O₄. From equilibrium composition of MnV₂O₄ in each sample as summarized in Table III, the stoichiometric coefficients of Mn, V, and O (or oxygen gas) in the above reactions can be derived.

To investigate the effect of nonstoichiometry of MnV₂O₄ on the Gibbs free energy of formation, $\Updelta g^\circ_{\rm f}$ of the non-stoichiometric MnV₂O₄ ($\Updelta g^\circ_{{\rm f,Mn}_{x} {\rm V}_y {\rm O}_{(x+1.5y)}},$ hereafter) for Reactions [C2] and [C3] were calculated by considering the following equations:

$$ \Updelta g^\circ_{{\rm f,Mn}_{x}{\rm V}_{y}{\rm O}_{({x}+1.5{y})}} = -\hbox{R}T\hbox{ln}\left(\frac{a_{{{\rm Mn}}_x\hbox{V}_y\hbox{O}_{(x+1.5y)}}}{a^x_{\underline{{\rm Mn}}}a^y_{\underline{{\rm V}}}a^{x+1.5y}_{\underline{{\rm O}}}}\right) \quad (\hbox{in liquid Fe}) $$

(C4)

$$ \Updelta g^\circ_{{\rm f,Mn}_{x}{\rm V}_{y}{\rm O}_{({x}+1.5{y})}} = -\hbox{R}T\hbox{ln}\left(\frac{a_{{\rm Mn}_x{\rm V}_y{\rm O}_{(x+1.5y)}}}{a^x_{{\rm Mn}}a^y_{{\rm V}}p^{(x+1.5y)/2}_{{\rm O}_{2}}}\right) \quad (\hbox{in liquid Cu}) $$

(C5)

Then, $\Updelta g^\circ_{{\rm f,Mn}_{x}{\rm V}_{y}{\rm O}_{({x}+1.5{y})}}$ from constituent oxides (Reaction [C1]) was determined and compared with the values of stoichiometric MnV₂O₄ as shown in Figure C1. In the figure, $\Updelta g^\circ_{{\rm f,Mn}_{x}{\rm V}_{y}{\rm O}_{({x}+1.5{y})}}$ and $\Updelta g^\circ_{{\rm f,MnV}_{2}{\rm O}_{4}}$ values are close to each other around the stoichiometric MnV₂O₄ composition, but they show discrepancies as the composition of MnV₂O₄ moves away from the stoichiometric value. It also indicates that the $\Updelta g^\circ_{{\rm f,Mn}_{x}{\rm V}_{y}{\rm O}_{({x}+1.5{y})}}$ values are dependent on oxygen partial pressure, which is the opposite of the result in Section III–B. In the current study, however, $\Updelta g^\circ_{{\rm f, MnV}_2{\rm O}_4}$ is recommended for the following reasons:

• (a) In terms of practical application of $\Updelta g^\circ_{{\rm f,MnV}_{2}{\rm O}_{4}},$ the reaction of stoichiometric MnV₂O₄ formation described as Eq. [1] is preferred, rather than Eq. [C1].

• (b) Around the stoichiometric MnV₂O₄ concentration, both $\Updelta g^\circ_{{\rm f, MnV}_2{\rm O}_4}$ and $\Updelta g^\circ_{{\rm f,Mn}_{x}{\rm V}_{y}{\rm O}_{({x}+1.5{y})}}$ are similar to each other.

Subsequent investigations are necessary to describe $\Updelta g^\circ_{{\rm f,MnV}_{2}{\rm O}_{4}}$ on the entire MnV₂O₄ solid solution range.

Fig. C1

Calculated $\Updelta g^\circ_{{\rm f,}}$ values of stoichiometric and nonstoichiometric MnV₂O₄ from its constituent oxides (MnO and V₂O₃) and the effect of oxygen partial pressure on the values. All lines are to guide the eye (Online version in color)

D. Enthalpy of Formation Estimated from the Gibbs Free Energy of Formation

The enthalpy of formation of an oxide spinel can be estimated in a simple way by subtracting the entropy contribution from its Gibbs free energy of formation. Jacob[28] suggested an empirical equation of entropy of formation of cubic 2 to 3 spinels from conponent oxides of rock salt and corundum structure:

$$ \Updelta S^{\circ}_{\rm f} = -7.32 + \Updelta S^{\rm CM} + \Updelta S^{\rm rand}_{\rm J T} $$

(D1)

where $\Updelta S^{\rm CM}$ is the configurational entropy of the crystal due to cation mixing and $\Updelta S^{\rm rand}_{\rm J T}$ is the entropy from randomization of the direction of Jahn-Teller distortions. For more details, the readers are invited to the relevant articles by Jacob,[28] and Jacob and Pandit.[27]

The configurational entropy of the oxide spinel could be calculated from cation distribution in tetrahedral and octahedral sublattices. In the case of MnV₂O₄ spinel structure, cation distribution of normal spinel MnV₂O₄ at 300 K (27 °C) was proposed as [Mn ²⁺_0.75 V ³⁺_0.75 ]^T[Mn ²⁺_0.25 V ³⁺_1.75 ]^OO₄ from neutron diffraction data by Pannunzio-Miner et al.[30] but the temperature seems to too low to be extrapolated up to 1823 K (1550 °C) relevant to the current study. In the current study, cation distribution of MnV₂O₄ spinel structure at 1823 K (1550 °C) was calculated using octahedral site preference energies as suggested by Navrotsky and Kleppa.[29]

Generally, cationic configuration of a stoichiometric 2 to 3 oxide spinel AB₂O₄ is described as:

$$ [\hbox{A}^{2+}]^{\rm T}[\hbox{B}^{3+}]^{\rm O}_2\hbox{O}_4 = [\hbox{A}^{2+}_{\lambda}\hbox{B}^{3+}_{1-\lambda}]^{\rm T}[\hbox{A}^{2+}_{1-\lambda}\hbox{B}^{3+}_{1+\lambda}]^{\rm O} \hbox{O}_4 $$

(D2)

where λ is the fraction of divalent A ion on the tetrahedral site. In terms of cation interchange between the sublattices, the upper reaction could be also regarded as:

$$ [\hbox{A}^{2+}]^{{\rm T}} + [\hbox{B}^{3+}]^{{\rm O}} \rightarrow [\hbox{A}^{2+}]^{O} + [\hbox{B}^{3+}]^{{\rm T}} $$

(D3)

then enthalpy and entropy change of the spinel for the above reaction could be written as follows:

$$ H^{\rm O}_{\hbox{A}^{2+}} - H^{\rm O}_{{\rm B}^{3+}} = \Updelta H^{\rm int} = -\hbox{R}T\hbox{ln}\frac{(1-\lambda)^2}{\lambda(1+\lambda)} $$

(D4)

$$ \Updelta S^{\rm CM} = -\hbox{R}[\lambda \hbox{ln} \lambda + (1-\lambda)\hbox{ln}(1-\lambda) + (1-\lambda)\hbox{ln}\frac{(1-\lambda)}{2} + (1+\lambda)\hbox{ln}\frac{(1+\lambda)}{2}] $$

(D5)

where $H^{\rm O}_{\hbox{A}^{2+}}$ and $H^{\rm O}_{\hbox{B}^{3+}}$ are the octahedral site preference energy of A²⁺ ion and that of B³⁺ ion, respectively. For entropy change, it is reasonable to take only configurational entropy into account because nonconfigurational contributions to total entropy change were found to be negligible in 2 to 3 oxide spinels.[29] Using the Eq. [D4] and $H^{\rm O}_{\hbox{Mn}^{2+}}$ and $H^{\rm O}_{\hbox{V}^{3+}}$ values from the Reference 31, the fraction of Mn²⁺ on the tetrahedral site of MnV₂O₄ at 1823 K (1550 °C) was determined to be 0.796, a similar value compared with 0.75.[30] Then, by inserting the fraction of Mn²⁺ as λ into Eq. [D5] and using Eq. [D1], the entropy of formation and, subsequently, the enthalpy of formation of the MnV₂O₄ could be obtained.