Phase-Field Modeling of Sigma-Phase Precipitation in 25Cr7Ni4Mo Duplex Stainless Steel

Abstract

Phase-field modeling is used to simulate the formation of sigma phase in a model alloy mimicking a commercial super duplex stainless steel (SDSS) alloy, in order to study precipitation and growth of sigma phase under linear continuous cooling. The so-called Warren–Boettinger–McFadden (WBM) model is used to build the basis of the multiphase and multicomponent phase-field model. The thermodynamic inconsistency at the multiple junctions associated with the multiphase formulation of the WBM model is resolved by means of a numerical Cut-off algorithm. To make realistic simulations, all the kinetic and the thermodynamic quantities are derived from the CALPHAD databases at each numerical time step, using Thermo-Calc and TQ-Interface. The credibility of the phase-field model is verified by comparing the results from the phase-field simulations with the corresponding DICTRA simulations and also with the empirical data. 2D phase-field simulations are performed for three different cooling rates in two different initial microstructures. A simple model for the nucleation of sigma phase is also implemented in the first case. Simulation results show that the precipitation of sigma phase is characterized by the accumulation of Cr and Mo at the austenite-ferrite and the ferrite-ferrite boundaries. Moreover, it is observed that a slow cooling rate promotes the growth of sigma phase, while a higher cooling rate restricts it, eventually preserving the duplex structure in the SDSS alloy. Results from the phase-field simulations are also compared quantitatively with the experiments, performed on a commercial 2507 SDSS alloy. It is found that overall, the predicted morphological features of the transformation and the composition profiles show good conformity with the empirical data.

1 Introduction

Stainless steels with roughly equal amounts of the phases, austenite and ferrite, are called duplex stainless steels (DSS). DSS are used in applications where a combination of excellent corrosion resistance with very good mechanical properties is needed, e.g., tubing for chemical industries, heat exchangers, seawater applications, and as construction material in applications such as bridges and storage tanks. For DSS with a pitting resistance equivalent over 40 in both austenite and ferrite the material is denoted as super duplex stainless steel (SDSS),[1] but this enhanced corrosion resistance comes with an increased susceptibility for precipitation of harmful intermetallic phases, e.g., sigma phase and chi phase, during production and welding.[2,3] Due to its large negative impact on both the corrosion resistance and the mechanical properties, the precipitation of sigma phase in DSS and SDSS has been studied extensively.[4,5,6,7,8,9,10,11,12]

In line with the principles of Integrated Computational Materials Engineering (ICME),[13,14] where modeling and simulations are combined with critical experiments in order to accelerate materials development, accurate modeling of the sigma-phase precipitation in DSS and SDSS allows for process control and prediction of microstructure evolution. The kinetics of sigma-phase precipitation in DSS has been predicted using Avrami-type models.[12,15] Modeling of the precipitation of sigma phase in an austenitic stainless steel has been performed by Schwind et al.[16] using the DICTRA software. In their treatment, the nucleation stage was neglected. Sieurin and Sandström[17] modeled sigma-phase precipitation in the DSS 2205 using a nucleation model based on classical nucleation theory and a quasistatic growth model.[18] Quite recently, Wessman and Pettersson[19] also studied the growth of sigma phase in SDSS using Thermo-Calc and DICTRA softwares.

Despite the relative success of these treatments, in order to study the influences of grain morphology and concurrent grain growth and precipitation, the phase-field method is preferred.[20] The method stems from the diffuse-interface concept: the one introduced by van der Waals for the smooth change of the density between a liquid phase and a gas phase, and independently proposed by Landau and Lifshitz[21] and by Cahn and Hilliard[22,23] for the excess free energy of the wall between two magnetic domains in a ferromagnetic material and for the liquid–gas surface respectively. The microstructure is described with one or more field variables, e.g., density or magnetic order, time evolutions of which are governed by a set of kinetic equations.[24,25] The phase-field method was first mainly used to model solidification in pure melts.[26,27,28] However, Wheeler, Boettinger, and McFadden further made a development and used the phase-field method to study solidification in binary alloys.[29,30,31] The so-called Wheeler–Boettinger–McFadden (WBM) model laid the foundation of the modern phase-field method.

Steinbach et al. used a different approach and presented the first phase-field model capable of simulating interactions between an arbitrary number of phases.[32,33] Tiaden et al.[34] incorporated a single-component diffusion model in the Steinbach multiphase-field model. Unlike the WBM model, which assumes that at an interface each phase has the same composition, Tiaden’s model suggested that the interface should be modeled as a mixture of phases, each with a unique composition $x_{\alpha }$ corresponding to the phase $\alpha$. The multicomponent extension to the Tiaden’s model was first developed by Grafe et al.[35] However, in their model, the driving force for the diffusion was computed by taking the concentration gradient of the components and thus imposing a restriction on the model to be used for the dilute solutions only. Eiken et al.[36] later removed this limitation by taking the gradient of the diffusion potential as the driving force for diffusion.

A number of authors since then have used the phase-field method to study phase transformation in single, binary, and multiphase systems,[37,38,39,40] using both the WBM and the Steinbach approaches. Villanueva et al.[41] used the WBM approach and developed a multicomponent and multiphase model with fluid motion to study reactive wetting. However, they used arbitrary phase diagrams and assumed ideal solutions for Gibbs energies. Cogswell and Carter[42] suggested a new approach and developed a thermodynamic phase-field model to study the microstructural evolution with multicomponents and phases. However, their simulations were also based on an arbitrary case, and the parameters used in the phase-field formulation did not correspond to a physical system.

Despite the earlier development of the computational modeling, to the authors’ knowledge, not much work has been done to study the formation of sigma phase in DSS using the phase-field method. Fukumoto et al.[43] studied the prediction of sigma-phase formation in Fe-Cr-Ni-Mo-N alloy using experiments and Md-PHACOMP (Phase Computation) and compared the results with a multiphase-field model based on the models by Steinbach et al. as implemented in the software MICRESS.

In the current study, a general framework for modeling of precipitation in multiphase and multicomponent materials using the phase-field method is presented. The underlying principle of the model is the same as that presented by Villanueva et al.[41]; however, a numerical treatment is introduced in the modeling to avoid thermodynamic inconsistency especially at the triple junctions. Moreover, instead of using ideal solutions for Gibbs energies and analytic expressions for atomic mobilities, the kinetic and the thermodynamic parameters are derived directly from the CALPHAD databases; this can, however, be computationally expensive, and therefore, an interpolation scheme is used.[44] The model is applied to the precipitation of sigma phase in a SDSS 2507 alloy (Fe-25Cr-7Ni-4Mo, wt pct) under continuous cooling.

2 Phase-Field Formulation

In this work, phase-field modeling is used to investigate the precipitation and growth of sigma phase in a polycrystalline material. In the current section, however, a generalized phase-field model is formulated to simulate the multiphase and multicomponent diffusional transformation. In principle, the model can be extended to any number of phases and components, but simulating a large number of variables would not only generate a large amount of data but would also require extensive computational resources.

The basis of the given multiphase and multicomponent phase-field model is built on the foundation laid by the WBM model.[29,30,31] However, a natural extension of the WBM model from a binary system to a ternary or a higher system would cause a thermodynamic inconsistency at the multijunctions. Therefore, in this study, a modification is made in the WBM model to extend it to multiphase and multicomponent system, which is discussed later in this section.

Consider a system with N number of components and M number of phases. The Gibbs energy G of the system is then formulated as a functional of the composition $x_{i}$ of each component and phase fraction $\phi _{\alpha }$ of each phase, where $i=1\ldots N$ and $\alpha =1\ldots M$.

$$\begin{aligned} G=\intop \left( \frac{G_{m}\left( x_{i},\phi _{\alpha },T\right) }{V_{m}}+\sum _{\alpha ,\beta =1}^{M-1}\frac{\epsilon _{\alpha \beta }^{2}}{2}\nabla \phi _{\alpha }\cdot \nabla \phi _{\beta }\right) \end{aligned},$$

(1)

where $V{}_{m}$ is the molar volume, assumed to be constant, and T is the temperature. In this study, simulations are performed for continuous cooling, and therefore, the molar Gibbs energy $G{}_{m}$ is given as a function of temperature as well. The second term in Eq. [1] is the contribution of the interfacial energy to the total Gibbs energy and is thus given as the sum of the products of the gradient of $\phi _{\alpha }$ and $\phi _{\beta }$ multiplied by the square of the corresponding interfacial energy coefficient $\epsilon _{\alpha \beta }$. In the given framework of equations, $x_{i}$ is a conserved quantity representing the mole fraction of N components, while $\phi _{\alpha }$ is a nonconserved parameter which is 1 in a particular phase and goes smoothly to 0 in all other phases. Here the term ’phase’ signifies a region with homogeneous properties having a distinct thermodynamic state and the crystallographic orientation. For a system with N components and M phases, the compositions and the phase fractions obey the following constraints, respectively:

$$\begin{aligned} \sum _{i=1}^{N}x_{i}=1 \end{aligned}$$

(2)

$$\begin{aligned} \sum _{\alpha =1}^{M}\phi _{\alpha }=1 \end{aligned}$$

(3)

2.1 Phase Evolution

Following the standard WBM model, $G{}_{m}$ of a multiphase system is formulated as follows.

$$\begin{aligned} G_{m}=\sum _{\alpha =1}^{M}p\left( \phi _{\alpha }\right) G_{m}^{\alpha }+\sum _{\alpha \ne \beta }W_{\alpha \beta }\phi _{\alpha }^{2}\phi _{\beta }^{2} \end{aligned},$$

(4)

where the first term is the sum of the molar Gibbs energy of each phase, weighted with the corresponding smoothed step function $p(\phi _{\alpha })=\phi _{\alpha }^{3}\left( 10-15\phi _{\alpha }+6\phi _{\alpha }^{2}\right)$. The second term represents the energy barrier between two phases, where $W_{\alpha \beta }$ is the energy barrier coefficient and is related to the thicknesses and the surface energies of the interfaces. Although the WBM model was initially formulated for a binary system, a natural extension to the ternary (or even higher) systems could be made by introducing $M-1$ number of $p(\phi _{\alpha })$ functions for a system with M phases. The step function for the $M^{th}$ phase would then follow the dependency constraint (Eq. [3]) and is given as $p\left( \phi _{M}\right) =1-\sum _{\alpha =1}^{M-1}p\left( \phi _{\alpha }\right)$. However, as mentioned earlier, this form of molar Gibbs energy would violate the condition given in Eq. [3] and lead to thermodynamic inconsistency, specifically at multijunctions. For instance, for a three-phase system, such a framework of equations would result in negative phase fractions at the triple junctions. Therefore, in order to overcome this issue, a Cut-off function,[42] introduced in Sect. II–A–1, is used, which ensures that the phase fractions obey the dependency constraint and hence guarantees the thermodynamic consistency.

Finally, the evolution of phase fractions is governed by the Allen-Cahn dynamics,[25] as follows:

$$\begin{aligned} \frac{\partial \phi _{\alpha }}{\partial t}=-M_{\phi _{\alpha }}\frac{\delta G}{\delta \phi _{\alpha }} \end{aligned},$$

(5)

where $M_{\phi _{\alpha }}$ is a kinetic coefficient that is related to the interfacial mobility M, and is derived from the literature.[45] The term on the right-hand side in the above equation is determined by taking the variational derivative of the Gibbs energy functional, given in Eq. [1]:

$$\begin{aligned} \frac{\delta G}{\delta \phi _{\alpha }}=\frac{1}{V_{m}}\frac{\partial G_{m}}{\partial \phi _{\alpha }}-\sum _{\beta =1}^{M-1}\epsilon _{\alpha \beta }^{2}\nabla ^{2}\phi _{\beta }. \end{aligned}$$

(6)

2.1.1 Cut-off function

A very standard condition of the phase-field method is that the expression for $G_{m}$ is constructed in such a way that the phase-field variable $\phi$ remains positive and less than or equal to 1. This is typically done by giving infinite penalty to $G_{m}$ for $\phi <0$ and $\phi >1$, thus prohibiting the formation of negative phases. However, an expression like the one given in Eq. [4] violates this condition for more than two phase-field variables resulting in unphysical phase fractions. A Cut-off function is therefore introduced to constrain the phase fractions within the allowed limit. The algorithm works on the principle that enforcing all M phase fractions to be positive, in the presence of the dependency constraint, automatically ensures that all phase fractions are restricted between 0 and 1. The working principle of the Cut-off function in case of three phases is given as follows.

Consider a system with three phases $\phi _{1}$, $\phi _{2},$ and $\phi _{3}$. The permissible zone for these phases is defined as the region where all the phase fractions are positive and satisfy Eq. [2]. The permissible zone in this case is represented by a triangle as shown in Figure 1 with two independent phases $\phi _{1}$ and $\phi _{2}$, at the horizontal and the vertical axes, respectively. The dependent phase $\phi _{3}$ is 1 at the origin where $\phi _{1}$ and $\phi _{2}$ are 0, and is 0 at the edge of the triangle represented by the broken line connecting the points where $\phi _{1}=1$ and $\phi _{2}=1$. Now, if the solution of Eq. [5] becomes unphysical, i.e., it leads to any of the independent phase fractions lying outside this triangle, a correction is made by projecting the unphysical phase fraction toward the permissible zone and setting it to zero. The dependent phase fraction is then determined using Eq. [3]. A slightly complicated situation arises when the dependent phase fraction $\phi _{3}$ becomes negative. In that case, correction is made by projecting $\phi _{3}$ in the direction perpendicular to line where $\phi _{3}=0$, toward the permissible space. Furthermore, in order to satisfy the dependency constraint, an equal portion of the unphysical phase fraction is then subtracted from each independent phase, i.e., $\phi _{1}$ and $\phi _{2}$.

A schematic description of such a scenario is also given in Figure 1, where the solution of Eq. [5] causes the evolution of phase fractions from point A to point B. Since point B lies outside the permissible zone, a correction is made using the Cut-off function giving new phase fractions, represented by point C. The algorithm can be generalized for a system with M phases, as given in Algorithm 1.[42,46]

Fig. 1

A schematic description of working principle of the Cut-off function in case of unphysical phase fractions

2.2 Compositional Evolution

The evolution of compositions is governed by the standard mass-conservation equation.

$$\begin{aligned} \frac{1}{V_{m}}\frac{\partial x_{i}}{\partial t}=-\nabla \cdot J_{i} \end{aligned},$$

(7)

where $J_{i}$ is the diffusional flux of component i and is given by the Onsager linear law of irreversible thermodynamics.

$$\begin{aligned} J_{i}=-\sum _{j=1}^{N-1}L_{ij}^{\prime \prime }\nabla \left( \frac{\delta G}{\delta x_{j}}\right) \end{aligned}$$

(8)

Using the dependency constraint on compositions (Eq. [2]), the diffusional flux assumes the following form:

$$\begin{aligned} J_{i}=-\frac{1}{V_{m}}\sum _{j=1}^{N-1}L_{ij}^{\prime \prime }\nabla \left( \mu _{j}-\mu _{N}\right) \end{aligned},$$

(9)

where $\mu _{j}$ is the chemical potential of $j^{th}$ component, while $\mu _{N}$ is the chemical potential of the dependent component. Since G is formulated as a function of phase fraction $\phi$, $\mu _{j}$ is also a function of $\phi$, given as the sum of chemical potential of component j in phase $\alpha$ multiplied by the step function, $p(\phi _{\alpha })$ of that phase. $L_{ij}^{\prime \prime }$ is a matrix of phenomenological coefficients that are related to the atomic mobilities $M_{i}\left( \phi \right)$ of the components, as follows[47]:

$$\begin{aligned} L_{ki}^{\prime \prime }=\sum _{j=1}^{n}\sum _{r=1}^{n}\left( \delta _{ir}-x_{i}\right) \left( \delta _{jk}-x_{k}\right) L_{jr} \end{aligned},$$

(10)

where $L_{kk}=x_{k}M_{k}\left( \phi \right)$ with $L_{kj}=0$ for $k\ne j$.

3 Physical Parameters

To study the evolution of sigma phase in a commercial duplex stainless steel alloy, the 2507 duplex grade with 64 pct Fe, 25 pct Cr, 7 pct Ni, and 4 pct Mo[1] is chosen. C and N, although vital elements in the commercial 2507 duplex grade, are neglected in the simulations due to their negligible influence on the precipitation and growth of sigma phase. Moreover, increasing the number of components from four to six would have had a significant effect on the computational cost. In the simulations, Fe is arbitrarily taken as the dependent or the $N^{th}$ component, and sigma is chosen as the $M^{th}$ phase. It should be noted that this choice has no effect on the simulation results.

For a three-phase system, i.e., austenite ($\gamma$), ferrite ($\alpha$) and sigma ($\sigma$) with three grains ($M=3$), the kinetic parameter $M_{\phi _{\alpha }}$, in Eq. [5], is taken as

$$\begin{aligned} M_{\phi _{\alpha }}=\frac{0.235}{\delta }M=\frac{0.235}{\delta }4\times 10^{-7}\mathrm {exp}\left( \frac{-140000}{RT}\right) \end{aligned},$$

(11)

where $\delta$ is the thickness of the diffused interface and is assumed to be constant, i.e., $2\times 10^{-9}m$. Interface mobility M is assumed to be same for all the phases. The interfacial energy coefficient $\epsilon _{\alpha \beta }$ and the energy barrier coefficient $W_{\alpha \beta }$ are given as a function of the interface thickness ($\delta$) and the interfacial energy ($\rho _{\alpha \beta }$).[38]

$$\begin{aligned} \epsilon _{\alpha \beta }^{2}=3\sqrt{2}\rho _{\alpha \beta }\delta \end{aligned}$$

(12)

$$\begin{aligned} W_{\alpha \beta }=\frac{6\rho _{\alpha \beta }V_{m}}{\sqrt{2}\delta } \end{aligned}$$

(13)

In this work, with austenite ($\gamma$), ferrite ($\alpha$), and sigma ($\sigma$) phases, the values of interfacial energy are chosen arbitrarily and are given as follows: $\rho _{\alpha \gamma }=1 J/m^{2}$, $\rho _{\alpha \sigma } = 0.5 J/m^{2},$ and $\rho _{\gamma \sigma } = 0.8 J/m^{2}$. The molar volume $V_{m}$ is, however, constant and is chosen to be $7\times 10^{-6} m^{3}/mol$.

For a system with four components ($N=4$), $L_{ij}^{\prime \prime }$ in Eq. [9], is 3$\times$3 symmetric matrix with 6 independent components. For cross diffusion, for instance, for Cr and Ni, $L_{CrNi}^{\prime \prime }$ is obtained by using Eq. [10], and is given as follows:

$$\begin{aligned} L_{CrNi}^{\prime \prime }=x_{Cr}x_{Ni}\left\{ -\left( 1-x_{Cr}\right) M_{Cr}\left( \phi \right) -(1-x_{Ni})M_{Ni}(\phi )+x_{Mo}M_{Mo}\left( \phi \right) +x_{Fe}M_{Fe}\left( \phi \right) \right\} \end{aligned}$$

(14)

For self diffusion, for instance, for Ni, $L_{NiNi}^{\prime \prime }$ is given as

$$\begin{aligned} L_{NiNi}^{\prime \prime }=x_{Ni}\left\{ \left( 1-x_{Ni}\right) ^{2}M_{Ni}(\phi )+x_{Cr}x_{Ni}M_{Cr}\left( \phi \right) +x_{Mo}x_{Ni}M_{Mo}\left( \phi \right) +x_{Fe}x_{Ni}M_{Fe}\left( \phi \right) \right\}. \end{aligned}$$

(15)

Other components in the $L_{ij}^{\prime \prime }$ matrix follow the same pattern. Atomic mobility of the components, i.e., $M_{i}(\phi )$ is modeled as the sum of the mobility in each phase linearly weighted with the corresponding phase fraction.

$$\begin{aligned} M_{i}\left( \phi \right) =M_{i}^{\alpha }\phi _{\alpha }+M_{i}^{\gamma }\phi _{\gamma }+M_{i}^{\sigma }(1-\phi _{\alpha }- \phi _{\gamma }). \end{aligned}$$

(16)

A very important feature of this phase-field model is that instead of choosing the ideal solutions, the kinetic and thermodynamic quantities, such as the Gibbs energies ($G_{m}^{\alpha }$), first derivative of the Gibbs energies with respect to the mole fractions, and the atomic mobilities ($M_{i}^{\alpha }$), are taken directly from the CALPHAD databases, at each numerical time step.[44] For this purpose, a coupling is made between the phase-field model and the Thermo-Calc Software[48] using the TQ-Interface.[49] For the thermodynamics, TCFE7[50] and for the mobilities, MOBFE2[51] databases are used.

4 Numerical Details

The model is developed and run in FemLego,[52,53] which is an open-source symbolic tool to solve partial differential equations using the adaptive finite element method. Different scenarios under different initial conditions are simulated to study the formation of sigma phase in 2507 DSS alloy under continuous cooling; the details of which are given in Sect. V. For boundary conditions, the no-flux or natural boundary condition is taken for both the composition and the phase evolution equations. This eventually would cause the boundary integral term to vanish in the weak form of both equations. The equations are discretized in space using the piecewise linear functions, and the linear system of equations is then solved using the conjugate gradient method.

Fig. 2

An example of adaptive meshing with refined mesh at the interfaces and coarsen mesh in the bulk phase. Colors represent different grains

A necessary condition of the phase-field model is to have a well-resolved interface, which makes the use of the adaptive mesh indispensable. Adaptive meshing is therefore used in the numerical modeling, based on an error criterion, given as a function of the gradients of compositions and phase fractions. The error criterion is chosen in such a way that it gives refined mesh only in the vicinity of the interfaces and a rather coarse mesh in the bulk domain. A typical example of adaptive meshing in FemLego is shown in Figure 2.

5 Results and Discussion

The results presented in this section are from numerical simulations performed on 2507 DSS alloy under continuous cooling. Colors in the figures showing microstructure represent phase fraction of a particular phase with the value of the phase-field variable of that phase between 0.5 and 1. The detail of each case is given below.

5.1 Sigma-Phase Formation in 1D Structure

In the first case, the growth of sigma phase is simulated in a 1D structure of the DSS alloy. The initial microstructure is shown in Figure 3(a), with equal fractions of austenite (red) and ferrite (green) phases present from the start. A thin layer of sigma phase (blue) is also introduced as the initial nucleus, to initiate the growth of sigma phase. The primary reason for doing this kind of simplistic 1D simulation is to validate the model by comparing the results from the phase field to the ones obtained from a sharp interface model like DICTRA.[48] The width of the rectangular domain is taken as 0.2 μm and the initial compositions of Cr, Mo, and Ni are set close to the equilibrium composition of each component in the given alloy at 1273 K (1000 °C), as taken from Thermo-Calc.

Fig. 3

(a) Initial and (b) final microstructures of 1D simulation. Colors represent different phases with red as austenite phase, green as ferrite phase, and blue as sigma phase. Numbers at the bottom depict volume fraction of each phase in percentage

The alloy is cooled down linearly from 1273 K to 950 K (1000 °C to 677 °C) at the cooling rate of 1 K/s, and the evolution of sigma phase is monitored with the decreasing temperature. Since sigma phase is stable at 1273 K (1000 °C) and lower, it starts to grow as the temperature is reduced. As the transformation is diffusion based and the sigma phase has higher diffusivity in ferrite than in austenite, sigma grows faster into the ferrite phase. There is almost 50 pct decrease in the fraction of ferrite, which is mostly consumed by sigma, while there is only 4 pct decrease in the fraction of austenite. Figure 3(b) shows the final microstructure as the temperature of the system reaches 950 K (677 °C).

To validate the phase-field model, results from the above case are compared to the results obtained from an identical simulation carried out in DICTRA. Figure 4 shows a comparison of the results for the compositions of Cr, Mo, and Ni, and the fraction of sigma phase as a function of temperature. The compositions are taken along the horizontal axis of the domain at the instant when the temperature reaches 950 K (677 °C). As evident from the plots given in Figure 4, the comparison shows quite a good agreement between the sharp-interface model and the diffuse-interface model.

Fig. 4

Comparison of phase-field results with DICTRA simulation: compositional profiles of (a) Cr, (b) Mo, and (c) Ni, along the horizontal axis: and (d) volume fraction of sigma phase as a function of temperature

5.2 Nucleation and Growth of Sigma Phase in a 2D Microstructure

To attain the duplex structure of austenite and ferrite phases in DSS, in practice, the alloy is generally heat treated at higher temperatures for a certain period of time. An incorrect heat treatment could result in the precipitation of sigma phase while cooling it through the most critical temperature range of 1123 K to 873 K (850 °C to 600 °C). An optimal cooling rate is therefore very important in order to prevent the nucleation of sigma phase and at the same time avoiding being quenched in nitrides. To replicate this scenario, 2D simulations are performed under continuous linear cooling from 1373 K to 950 K (1100 °C to 677 °C) incorporating a simple model of nucleation. The initial microstructure consists of single grains of austenite (in red) and ferrite (in green) phases as shown in Figure 5(a). The size of the square computational domain is 0.5 μm × 0.5 μm. The initial compositions of Cr, Mo, and Ni, taken from Thermo-Calc at 1373 K (1100 °C), are given in Figures 5(b), (c), and (d), respectively. For nucleation of sigma phase, the driving force for precipitation of sigma phase is derived from Thermo-Calc, which is then compared to a critical driving force, at each numerical time step.

The driving force (DF) for forming sigma phase is calculated as the distance between parallel tangents or planes, in binary and ternary systems respectively, for the Gibbs energy curves/surfaces. In our case with four components, this distance is between tangent planes of higher order in composition space. The calculation is handled by Thermo-Calc, and DF is easily retrieved for general multicomponent alloys. The evaluated DF is compared to a critical DF set (arbitrarily) to R*T*1e-5 J/mol, where R is the gas constant and T is the temperature in Kelvin). When DFcalc>DFcrit, we “nucleate” sigma phase as a small elliptical nucleus placed at the austenite-ferrite boundary and vertically in the center of the domain. The size of the nucleus is chosen slightly larger than the critical size at the given temperature. The method to estimate the critical size of the nucleus is given in Appendix A.

Fig. 5

Initial configurations of (a) phase fraction, (b) Cr composition, (c) Mo composition, and (d) Ni composition, with austenite on the left side and ferrite on the right side

Simulations are performed for three different cooling rates, i.e., 1, 50 and 100 K/s. Figure 6 shows the snapshots of microstructures at four different instants in temperature for the three cooling rates. With a slower cooling rate, i.e. 1 K/s, initially, the austenite grows into the ferrite as the temperature is decreased. At around 1290 K (1017 °C), the driving force for the nucleation of sigma phase becomes high enough, consequently causing the nucleation of sigma phase (in blue) at the austenite-ferrite boundary. Upon further cooling, the initial nucleus of sigma phase first shrinks until the temperature reaches around 1250 K (977 °C), after which it starts to grow. As the temperate is further reduced, a simultaneous growth of austenite and sigma phase is observed, as shown in Figure 6(a). By the time the temperature reaches 950 K (677 °C), there is a 32 pct decrease in the fraction of ferrite as it is reduced from 50 pct to around 18 pct. Ferrite is consumed both by the austenite and the sigma phases. There is almost 8 pct increase in the fraction of austenite, mostly consumed by the sigma phase, which itself attains a volume fraction of almost 23 pct at 950 K (677 °C). The slow cooling rate, therefore, not only causes the growth of intermetallic phases in the alloy but also disturbs the duplex fraction ratio of the austenite and the ferrite phases in the DSS.

Fig. 6

Microstructural evolution with the cooling rates of (a) 1 K/s, (b) 50 K/s, and (c) 100 K/s, at different points in temperatures, where (a1), (b1), and (c1) are at 1250 K (977 °C); (a2), (b2), and (c2) are at 1150 K (877 °C); (a3), (b3), and (c3) are at 1050 K (777 °C); and (a4), (b4), and (c4) are at 950 K (677 °C). Red is austenite, green is ferrite and blue is sigma phase. Numbers at the bottom depict volume fraction of each phase in percentage

With the higher cooling rates, i.e., 50 K/s (Figure 6(b)) and 100 K/s (Figure 6(c), there is no significant change in the volume fractions of austenite and ferrite phases as the temperature is reduced. Sigma phase nucleates at around 1295 K (1022 °C) for 50 K/s and at 1293 K (1020 °C) for 100 K/s. Although the nucleation temperature of sigma phase is slightly higher with the faster cooling compared with the slow cooling, the final volume fraction of sigma phase is considerably low. In fact with 100 K/s, the growth of sigma phase is completely restricted with a very little change in the fraction of the initial nucleus. Moreover, the initial volume fractions of austenite and ferrite phases are also preserved. Hence, as a preliminary conclusion, it can be stated that to avoid the precipitation of sigma phase and to keep the 50–50 fraction ratio of austenite and ferrite phases in DSS, a higher cooling rate should be preferred, which is also in agreement with the experimental observations.

It is observed empirically that Cr and Mo are enriched in the ferrite phase, while Ni is majorly accumulated in the austenite phase.[54] Sigma phase is also enriched with Cr and Mo even to a higher degree than those in ferrite phase. Looking at the compositional profiles of Cr, Mo, and Ni at the instance when temperature reaches 950 K (677 °C), in Figure 7, a similar behavior is observed in the simulation results as well.

Fig. 7

Compositional profiles of (a) Cr, (b) Mo, and (c) Ni as the temperature reaches 950 K (677 °C) for three different cooling rates: (a1), (b1), and (c1) with 1 K/s; (a2), (b2), and (c2) with 50 K/s; and (a3), (b3), and (c3) with 100 K/s), with austenite on the left side, ferrite on the right side, and sigma in the middle

Since sigma phase is a Cr-rich phase, most of the Cr is accumulated inside the sigma phase for all the three cooling rates, as shown in Figure 7(a). This accumulation of Cr also creates a depletion zone at the austenite-sigma and the sigma-ferrite boundaries, depicted by the dark blue and the light blue regions, respectively. Ferrite has a higher Cr content than austenite. As the diffusional mobility in sigma phase is much lower than that of austenite and ferrite phases, the initial composition also changes very slowly.

Mo also has a higher concentration in sigma phase, consequently leading to depletion zones at the austenite-sigma and the sigma-ferrite boundaries, Figure 7(b). These Cr- and Mo-depleted zones are also believed to be one of the reasons of the reduction in the corrosion resistances of DSS and SDSS alloys.[54,55] For the slowly cooled alloy (1 K/s), most of the Mo is diffused into the sigma phase, consequently leading to a low Mo content in the ferrite. Another reason for the low Mo content in ferrite is the thin region of the ferrite grain, which lies within the Mo-depletion zone. With faster cooling rates, i.e., 50 and 100 K/s, however, the ferrite phase is characterized by a higher Mo content than that of austenite.

Fig. 8

Volume fractions of (a) ferrite, (b) austenite, and (c) sigma phases as a function of temperature with cooling rates of 1 K/s (blue-squares), 50 K/s (red-diamonds), and 100 K/s (green-circles)

For the three cooling rates, Ni concentration is found to be higher in the austenite phase, while sigma phase is characterized by a low Ni content. With the slow cooling rate, i.e., 1 K/s, however, a thin layer of higher Ni concentration is observed at the austenite-sigma interface, as can be seen in Figure 7(c), which is not found with the faster cooling rates. The primary reason of the accumulation of Ni could be the curved profile of the austenite-sigma interface with the slow cooling compared with a rather flat profile with the faster cooling.

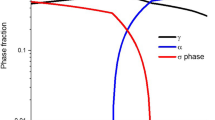
Figure 8 shows the plots of volume fraction of ferrite, austenite, and sigma phases as a function of temperature, for three cooling rates. With 1 K/s, a significant decrease in the fraction of ferrite phase is observed, as it is reduced from 50 to 18 pct. Austenite, on the other hand, is promoted with the decreasing temperature, showing almost an 8 pct increase in the volume fraction. Sigma phase, being stable at lower temperature, is highly promoted with the slow cooling rate. With 1 K/s, sigma phase attains a volume fraction of 23 pct as the temperature reaches 950 K (677 °C). It is obvious from the plots that a higher cooling rate, i.e., 50 K/s, plays a significant role in keeping the duplex structure of the alloy. Slight decreases in the fractions of ferrite and austenite are mainly due to the introduction of the initial nucleus of sigma phase. The restricted growth of sigma phase with high cooling rates is also a manifestation of the fact that faster cooling prevents the precipitation of sigma phase. Similar results are obtained with 100 K/s as well, without any considerable change in the volume fractions of the phases. It can also be seen from the plots that a higher rate than an optimal cooling rate will have no or very little effect on the growth of sigma phase.

5.3 Formation of Sigma Phase in a 2D Polycrystalline Microstructure

Real structures are of course polycrystalline in nature, and therefore, in order to replicate a real case scenario, 2D simulations are performed with multiple grains of austenite and ferrite phases. The initial microstructure is shown in Figure 9, having different grains of austenite (red and purple) and ferrite (yellow and green). The width of the computational domain is taken as 1 μm with a height of 1.3 μm. The alloy is cooled down linearly from 1273 K to 950 K (1000 °C to 677 °C) with cooling rates of 1, 50, and 100 K/s. Two circular nuclei of sigma phase are placed in the domain to initiate the formation of the brittle phase. The position of the nuclei is chosen arbitrarily, but since triple junctions are found to be a potential site for the nucleation of sigma phase,[55] the nuclei are placed at the triple junctions. Initial composition of the alloying elements is chosen close to the equilibrium composition at 1273 K (1000 °C).

Fig. 9

Initial microstructure with different grains of austenite (red and purple), ferrite (yellow and green), and sigma (blue) phases. Numbers at the bottom depict volume fraction of each phase in percentage

Figure 10 shows the snapshots of microstructure at different instants in temperature as the alloy is cooled down with 1 and 100 K/s. Results obtained from the cooling rate of 50 K/s demonstrated similar behavior as the ones obtained from 100 K/s and are therefore not shown in the figure below. With slow cooling rate, i.e., 1 K/s, as the temperature is reduced, the initial nuclei first tend to shrink until the temperature reaches 1240 K (967 °C), but as the temperature is further reduced, the nuclei start to grow. As the temperature reaches around 1165 K (892 °C), new domains of sigma phase are formed at the triple junctions, highlighted by the black circles in Figure 10(a). The primary reason for the formation of these domains is the accumulation of Cr at the nucleation site. Further decrease in the temperature not only causes coarsening of the existing domains but also forms new domains of sigma phase at the triple junctions. At 1050 K (777 °C), almost 15 pct of the alloy is transformed to sigma phase with most of it forming at the austenite-ferrite and the ferrite-ferrite boundaries.

Fig. 10

Microstructural evolutions with the cooling rates of (a) 1 K/s and (b) 100 K/s, at different points in temperatures ((a1) and (b1) at 1165 K (897 °C); (a2) and (b2) at 1120 K (847 °C); (a3) and (b3) at 1050 K (777 °C); and (a4) and (b4) at 950 K (677 °C)), with austenite (red and purple), ferrite (yellow and green), and sigma (blue) phases

Slow cooling of the alloy and the precipitation of sigma phase consequently decrease the fraction of ferrite but cause an increase in the fraction of austenite. As the alloy is cooled down to 950 K (677 °C), ferrite is reduced to almost half of its initial amount, while a slight increase in the fraction of austenite is observed. Cooling the alloy with a higher cooling rate, i.e., 100 K/s, however, does not promote the growth of sigma phase, as shown in Figure 10(b). As the temperature is reduced from 1273 K to 950 K (1000 °C to 677 °C), apart from a slight rearrangement, no significant changes in the volume fractions of the phases are observed.

Fig. 11

Volume fractions of (a) ferrite, (b) austenite, and (c) sigma phases as a function of temperature with cooling rates of 1 K/s (blue-squares), 50 K/s (red-diamonds), and 100 K/s (green-circles)

A comparison of the volume fractions of ferrite, austenite, and sigma phases under continuous cooling and with cooling rates of 1, 50, and 100 K/s, as shown in Figure 11, depicts the effect of cooling rate on the growth of sigma phase. With 1 K/s, by the time the temperature reaches 950 K (677 °C), the fraction of ferrite is reduced from 50 to 26 pct, while there is almost 3 pct increase in the fraction of austenite. This decrease in the fraction of ferrite is mainly due to the growth of sigma phase in the domain, which acquires a volume fraction of almost 18 pct. On the contrary, with 50 and 100 K/s, there is no significant change in the fraction of sigma phase, which changes from 0.7 to 1 pct. Moreover, apart from a slight contraction in the fraction of ferrite, which decreases from 50 pct to almost 45 pct, there is no considerable change in the initial microstructure. Hence, in conclusion, it can be stated that the slow cooling will promote the formation of sigma phase causing a decrease in the amount of ferrite; however, a higher cooling rate will not only restrict the growth or formation of sigma phase but will also tend to maintain the duplex microstructure of the DSS/SDSS.

5.4 Quantitative Comparison Between Experiments and Simulations

In order to demonstrate the capability of the phase-field model presented in this work, a quantitative comparison is made between experimental data and simulation results. Experiments are carried out on a 2507 SDSS alloy, and the empirical data are then compared quantitatively to the results obtained from the polycrystalline simulations. To achieve a similar cooling profile as in the polycrystalline simulation, the alloy is heat treated at 1353 K (1080 °C), after which it is cooled down from 1273 K to 950 K (1000 °C to 677 °C) with four different cooling rates: i.e., 1, 25, 50, and 100 K/s. Details of the experimental setup are omitted here since they fall outside the scope of this paper.

Fig. 12

Microstructure of 2507 SDSS alloy after cooling down from 1273 K to 950 K (1000 °C to 677 °C) with cooling rates: (a) 1 K/s and (b) 25 K/s. The white phase is austenite, the gray phase is ferrite, and the blue-brownish is sigma phase with small fractions of other intermetallic phases

The resulting microstructures for cooling rates of 1 and 25 K/s are shown in Figures 12(a) and (b), respectively. The precipitation of sigma phase is only observed with the cooling rate of 1 K/s with the sigma phase attaining a volume fraction of almost 16 pct. The fraction of sigma phase is in good agreement with the simulation results of polycrystalline microstructure where the predicted fraction of sigma phase is almost 18 pct. With higher cooling rates, however, no sigma phase is observed in the experiments. This is also in accordance with the simulation results where the predicted fraction of sigma phase is almost 1 pct with 50 and 100 K/s. This small fraction is due to the initial preplaced nucleus of sigma phase (having a volume fraction of 0.7 pct). Apart from slight readjustment of the initial nucleus and spotting of small regions of sigma phase at triple junction, no significant growth of sigma phase is observed in the simulations as well. It is seen in Figure 12(a) that sigma phase precipitates at the austenite-ferrite boundaries and grows mostly into the ferrite phase. This morphological behavior of sigma phase is also observed in the simulation results, Figure 10(a), where the sigma phase nucleates at the austenite-ferrite boundaries and at the triple junctions and grows into the ferrite phase.

Table I illustrates a comparison between the observed composition profiles of Cr, Mo, and Ni from the experiments and the mean predicted values from the phase-field simulations. For the simulation results, an average of the composition profile is taken over the whole domain of the particular phase from the polycrystalline simulation. Since sigma phase appears only with the cooling rate of 1 K/s, the data are obtained and compared with just one cooling rate. It can be seen that for Cr, the simulations predict slightly lower value in austenite and ferrite, and a higher value in sigma phase. The difference, however, is not too large and could be attributed to the sharp decrease in Cr concentrations at the interfaces (depletion zone) in the simulations, which consequently gives a lower mean value. In case of Mo, the mean predicted composition is in relatively good agreement with the observed concentration. For Ni, the predicted values are slightly higher in austenite and ferrite phases, while it matches quite well with the observed value in sigma phase. The difference, once again, is due to the spike in the concentration of Ni at austenite-ferrite and austenite-sigma interfaces, which gives a higher average value. Overall, however, the predicted composition profile is in good agreement with the observed concentration data, given the fact that the secondary elements (Si, Mn, etc.) are neglected in the simulation.

6 Conclusions

In this study, a multiphase and multicomponent phase-field model is presented based on the WBM model to study the formation of sigma phase in an alloy mimicking a commercial stainless steel alloy. To avoid thermodynamic inconsistency associated with the multiphase formulation of the WBM model, a numerical treatment is introduced. The thermodynamic and the kinetic parameters such as Gibbs energy, first derivative of Gibbs energy with respect to composition, and atomic mobilities are derived directly from the CALPHAD databases at each numerical timestep. The effect of elastic strain energy is neglected in the model since the precipitation of sigma phase is simulated only in base metals where there is no coherency between austenite/ferrite. It should be noted that the influence of elastic strain energy on the transformation is significant only in the cases where the austenite/ferrite interface is coherent and obeys the Kurdjumov–Sachs (K–S) orientation relationship. It has been shown by Sato and Kokawa[56] that, in base metals, the activation energy barrier for sigma-phase formation at the austenite/ferrite interface is lower due to large deviation from K–S orientation relationship, i.e., sigma phase can easily form. Hence, in such a case, one can neglect the influence of elastic strain energy on the nucleation of sigma phase. In addition, at these temperatures, the yield stresses of austenite and ferrite are in the order of 100 MPa,[57] which means that the elastic strain energy would be quite low and may not affect the transformation to a great extent.

The given model is finally applied to study the precipitation and growth of sigma phase in a SDSS alloy (Fe-25Cr-7Ni-4Mo, wt pct) during continuous cooling for different microstructures. A good agreement is found between 1D results from the phase-field simulations and the results obtained from a similar simulation carried out in DICTRA software, also proving the credibility of the diffuse-interface model. Simulations are performed with continuous cooling and at different cooling rates, incorporating a simple model of nucleation. Results show that higher cooling rates tend to restrict the growth of sigma phase in the given SDSS alloy, while a slow cooling rate promotes it. The primary reason of this behavior is the longer diffusion time for Cr and Mo with slow cooling rate, which eventually stabilizes the sigma phase. Moreover, it is observed that a higher cooling rate also preserves the duplex structures of austenite and ferrite phases in the DSS/SDSS alloy. Precipitation of sigma phase is also characterized by Cr- and Mo-rich regions, eventually creating Cr- and Mo-depletion zones at the austenite-sigma and the ferrite-sigma boundaries, which is also believed to be the major cause of the reduction in the corrosion resistances of the DSS and SDSS alloys.

Simulations are also performed in a polycrystalline structure with multiple grains of austenite and ferrite phases under continuous cooling. Results from the polycrystalline simulations illustrate that sigma phase tends to form at the austenite-ferrite and the ferrite-ferrite boundaries. The results obtained from the polycrystalline simulations are compared quantitativly with the empirical data. Results from the experiments, carried out on a commercial 2507 SDSS alloy, showed good quantitative agreement with the simulation results, which further establishes the capability of the phase-field model. A comparison of the experimental data also shows that the polycrystalline simulations exhibit better conformity with the empirical observations than the single grain simulations. The given phase-field model can thus be used to study the effects of alloying elements, different thermal conditions, and heat treatments on the precipitation and growth of sigma phase in DSS and SDSS alloys. Although C and N are important constitutive elements of the 2507 DSS alloy, they have been omitted in the simulations due to their causing little effect on the precipitation and growth of sigma phase in duplex grades. Moreover, adding more elements to the numerical model would increase the computational cost manyfold. The future work is, however, planned to verify this hypothesis by having a more efficient numerical scheme.

Appendix: Estimation of the Critical Size of Nucleus

The critical size of the nucleus is estimated using the following expression:

$$\begin{aligned} r^{*}=\frac{2\rho }{\Delta G_{m}}V_{m} \end{aligned}$$

(A1)

where $\rho$ is the corresponding interfacial energy and $\Delta G_{m}$ is the driving force for the precipitation of sigma phase. In order to verify the above expression, few numerical tests were made in a 2D case at different temperatures corresponding to different values of $\Delta G_{m}$ in the following pattern. A certain sized nucleus of sigma phase was placed at the austenite/ferrite phase boundary to observe its behavior at isothermal conditions. In case of growth of sigma phase, the size of the nucleus was reduced in the subsequent phase-field simulations until the nucleus started to shrink. In case of shrinkage, the size of the nucleus was increased in the subsequent simulations. The threshold value between shrinkage and growth of the nucleus was then taken as the critical size of the nucleus. It was found that the value of the critical size obtained from expression A1 was in agreement with the one predicted from the phase-field simulations.

Table I Average Composition Data of Cr, Mo and Ni as Obtained from Experiments and Phase-Field Simulation with Cooling Rate of 1 K/s. All the Values Are Given in mol pct