1 Introduction

Grain boundaries (GBs) that possess long-range atomic structural order tend to exhibit properties that strongly depend on the details of their structure. Details of interest include the atomic structure of the coherent regions (atomic density and periodicity) and the characteristics of the intrinsic grain boundary defects (such as screw/edge character, spacing, step height, and Burgers vector).[1,2] Based on these structural features, ordered GBs can potentially be grouped, with the intent of eventually correlating a group of GBs to a particular reaction response, for instance with an impinging lattice dislocation, or a response to an applied normal or shear traction.[3–9] In the current work, the atomic structures of symmetrical tilt grain boundaries (STGBs) in hexagonal close-packed (hcp) structures are studied. STGBs are simple grain boundaries that are fully described crystallographically by a tilt axis and tilt angle 2θ. For this class of boundaries, prior studies have investigated, for instance, the effect of GB defect structure on the propensity for sliding,[4,10] partial transmission and absorption,[4–9,11] and vacancy migration energies and entropies.[12,13]

Most atomic-scale structural models for STGBs have been developed for high-symmetry face-centered-cubic and body-centered-cubic crystals.[6,14–21] In this large body of work, the atomic structures of cubic STGBs, differing in tilt axis and continually varying over a wide range of θ, have been characterized using structural unit models or coincident site lattice (CSL) concepts. For hcp crystals, most atomistic studies, involving atomic-scale topological models, density functional theory, or molecular dynamics (MD),[22–36] have focused on coherent STGBs free of intrinsic grain boundary dislocations, such as twin boundaries (TBs). Among those studies using MD simulations, the structure predictions of the more common hcp \( (\bar{1}012),\;(\bar{1}011),\;(\bar{2}112) \), and \( (\bar{2}111) \) TBs employing different interatomic potentials and c/a ratios[12,23–28,30,37,38] were consistent, suggesting that their basic structural characteristics are properties of hcp topology. Additional coherent boundaries structures, such as \( (\bar{2}115),\;(\bar{2}116),\;(\bar{3}032),\;(\bar{3}034),\;(\bar{1}014) \), and \( (\bar{2}021) \), not associated with experimentally observed hcp twins, have also been modeled.[37–40]

Less comprehensively studied for hcp crystals are the changes in dislocation structure of STGBs as θ is continually varied in orientation space, in particular, as θ deviates from that of a coherent boundary. Generally, as θ tilts off coherency, intrinsic GBDs should form to accommodate the deviation, an expectation that has been confirmed experimentally.[41–43] Prior studies involving extensions of theories based on CSLs and structure unit models (SUMs) postulate that the STGBs that deviate from a nearby coherent (“favored”[18]) boundary in orientation space should contain some fundamental units or resemble that of the favored boundary,[11,37–39,42–47] apart from the distortions that result from the GBDs. Recently, we carried out a systematic study of STGB structure spanning the entire range of misorientations: 0 deg < 2 θ < 180 deg in Reference 3. In that work, we used molecular dynamics (MD) with interatomic potentials for Mg and Ti to create STGBs by rotating about the \( [1\bar{2}10] \) axis an arbitrary rotation angle θ and employed interfacial defect theory[3] to characterize their dislocation structure. In orientation space, six special rotation angles \( \theta_{B}^{(i)} \) corresponding to six crystallographic planes, \( P_{B}^{(i)} \), i = 1, …, 6, arose in simulation, which were associated with GB planes of zero or local minimum-energy STGBs. A key finding was that STGBs whose θ were close in orientation to one of these six \( P_{B}^{(i)} \) shared the same GB plane as \( P_{B}^{(i)} \) and contained GBDs with the same Burgers vectors. Significantly, based on this, we classify the \( [1\bar{2}10] \) STGBs into six structural sets.

In this work, we use the same tools to examine the dislocation structure of STGBs in hcp crystals generated by rotating about the \( [0\bar{1}10] \) axes. Our interest is to determine the changes in the relaxed atomic structures of \( [0\bar{1}10] \) STGBs as θ is varied continuously and whether the resulting assortment can be conveniently classified into, at most, a handful of distinct structural sets with fundamental features in common.

2 Atomistic Model of an STGB

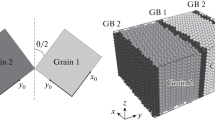
MD simulations are employed to calculate the relaxed atomic structures of STGBs with a tilt axis of \( [0\bar{1}10] \) over the entire range of θ. The model consists of a single grain boundary, as shown in Figure 1(a), which divides the top hcp crystal from the bottom one. The z axis is the tilt axis and the y axis is the GB plane normal. The top crystal rotates θ clockwise and the bottom one rotates θ counterclockwise about the z axis. We also introduce a local coordinate system, x’-y’-z’, for each crystal that rotates with θ, where x’-y’-z’ is \( [2\bar{1}\bar{1}0] - [0001] - [0\bar{1}10] \) and z’ = z, the tilt axis \( [0\bar{1}10] \). Figure 1(b) presents the corresponding MD simulation cell. The simulation model contains an internal moveable region 1 and an outer semirigid region 2 that acts as a flexible boundary to mimic the bulk response during relaxation.[48,49] Periodic boundary conditions are applied in the x and z directions. The x dimension varies with θ such that periodic boundary conditions are satisfied. For this work, the length of the periodic unit in x is less than 5.0 nm, and the x dimension is a few times the length of the periodic unit but not less than 10 nm. The height in y of the bi-crystal is 8.0 nm and the thickness in y of semi-rigid region is 1.2 nm, which is twice the cutoff of the potential used. The dimension in the z direction is ~2.2 nm containing eight periodic units.

Fig. 1
figure 1

(a) Illustration of a symmetrical tilt grain boundary. The green rectangles indicate the unit cell of the top and low crystals. The two crystals with initially the same orientation are rotated around the tilt axis by an angle θ. The grain boundary plane is the x-z plane. (b) The atomistic simulation cell. Periodic boundary conditions are adopted in both the x and z directions. The semirigid regions serve as a flexible boundary in the y direction and mimic the properties of the bulk material (Color figure online)

Full size image

The current MD calculations use interatomic potentials benchmarked either for magnesium (c/a = 1.623)[50,51] or alpha-titanium (c/a = 1.5873).[52] To create the STGB, the bicrystal model with a given tilt axis and angle is relaxed at 0 K (–273 °C) by quenching molecular dynamics. The relaxation process occurs in two steps to achieve the lowest energy structure.[53,54] First, during relaxation, the two crystals attain favorable positions and interface spacing by translating relative to one another as rigid bodies in the three orthogonal x-y-z directions. Rotation about the boundary normal, however, is prevented. A fine grid of 0.025 nm in x and z is used within a boundary-unit-cell (BUC)Footnote 1 for the displacements in the x-z plane.

Relaxation is performed for each interface structure corresponding to the displacement, leaving a series of different relaxed configurations varying in energy. Second, we select the five lowest energy configurations from the first step and relax each further by allowing all atoms to relax independently so that the net forces acting both parallel and perpendicular to the interface are minimized. A fully relaxed state is achieved when the maximum force acting on any atom in the system does not exceed 5 pN. The configuration with the lowest energy among the five is considered the relaxed atomic structure of the STGB.

3 Atomistic Calculations of Energy VS Tilt Angle 2θ

Figure 2 presents the calculated excess potential energy of STGBs in Mg as a function of θ. At the two extreme ends of the plot, θ = 0 deg and 90 deg, are zero-energy states corresponding to perfect crystals in which the GB y = y’-plane coincides with the basal plane when θ = 0 deg and the \( (\bar{2}110) \) plane when θ = 90 deg. In between these two states, we observe cusps in the excess potential energy vs θ plot, which are associated with coherent STGBs. These four STGBs have tilts θ B = 28.41 deg, 39.06 deg, 58.36 deg, and 72.88 deg, and these values correspond to planes \( P_{\text{B}} = (\bar{2}116),\;(\bar{2}114),\;(\bar{2}112) \), and \( (\bar{2}111) \), respectively (Figure 3). The atomic structures of these four STGBs are shown in Figure 4. The TB structures for \( (\bar{2}114),\;(\bar{2}112) \), and \( (\bar{2}111) \) agree with those predicted by other MD simulations using alternative potentials, which were developed for other c/a ratios.[12,39] The current calculations find that their formation energies vary substantially from 322.4 mJ/m2 and 351.6 mJ/m2 for \( (\bar{2}116) \) and \( (\bar{2}114) \) to 123.8 mJ/m2 and 71.1 mJ/m2 for \( (\bar{2}112) \) and \( (\bar{2}111) \). The same order in GB energy, i.e., \( (\bar{2}111) < (\bar{2}112) < (\bar{2}116) < (\bar{2}114) \), is also calculated by MD simulations in References 12, 24, 31, 39 using potentials designed for other hcp metals, Co, Zr, or Ti. Interestingly, for both the Mg and Ti potentials (described subsequently), neither the coherent \( (\bar{2}115) \) STGB (θ = 33 deg) nor the coherent \( (\bar{2}113) \) TB (θ = 47.26 deg) manifests. As will be discussed next, it seems to be more energetically favorable for the bicrystal to accommodate these two misorientations (θ = 33 deg and θ = 47.26 deg) with a GB plane consisting of intrinsic GBDs than as a coherent \( (\bar{2}115) \) STGB or \( (\bar{2}113) \) TB.

Fig. 2
figure 2

Excess potential energies of \( [0\bar{1}10] \) STGBs in Mg as a function of θ. The colored regions mark six sets, S-1 to S-6, and their ranges of θ within which STGBs can be viewed as having similar atomic structure. S-1 and S-6: an array of GBDs; S-2 to S-5: minimum-energy boundaries plus an array of GBDs (Color figure online)

Full size image
Fig. 3
figure 3

An hcp crystal lattice showing the four planes \( (\bar{2}111),\;(\bar{2}112),\;(\bar{2}114) \), and \( (\bar{2}116) \) that share a zonal axis parallel to \( [0\bar{1}10] \). The intermediate basis layers of the hcp crystal are omitted for clarity

Full size image
Fig. 4
figure 4

Atomic structures of four minimum-energy STGBs in Mg: (a) \( (\bar{2}116) \) boundary, (b) \( (\bar{2}114) \) twin boundary, (c) \( (\bar{2}112) \) twin boundary, and (d) \( (\bar{2}111) \) twin boundary. The left side shows the atomic structure of STGBs in the x-y plane, and the right side shows the atomic structure of STGBs in the y-z plane. When showing the y-z projection (right), it is necessary to use smaller sized atoms than the x-y projection (left) to reveal all atoms and any structural detail because the x direction is not along the compact direction. The red line indicates the twin boundary plane. Atoms are colored according their excess potential energy (Color figure online)

Full size image

4 Structural Sets of STGBs

The six special misorientation/GB plane pairs discussed previously, which are hereinafter denoted by \( \left( {P_{B}^{(i)} ,\;\theta_{B}^{(i)} } \right) \), i = 1, …, 6, are defect free: two correspond to a perfect crystal, with the virtual GB plane parallel to the basal plane (\( \theta_{B}^{(1)} \) = 0 deg) or the \( \left( {11\bar{2}0} \right) \) plane (\( \theta_{B}^{(6)} \) = 90 deg), and four correspond to coherent STGBs (Figures 3 and 4). MD simulations of STGBs that do not correspond to one of these six predict the development of a periodic array of discrete GBD. All \( [0\bar{1}10] \) STGBs over the entire range of possible θ, therefore, have an ordered atomic structure and can be described as tilt walls. The GBDs in all cases are oriented parallel to the tilt axis and are superimposed on the same boundary plane P B of the special STGB \( \left( {P_{B}^{(i)} ,\;\theta_{B}^{(i)} } \right) \) closest to it in orientation space. In other words, the plane P B serves as the base boundary structure of the STGB. Formation of the GBDs causes the significantly higher formation energies compared with those for its nearest minimum-energy STGB \( \left( {P_{B}^{(i)} ,\;\theta_{B}^{(i)} } \right) \). Because every STGB lies within the neighborhood of one of the six special STGBs \( \left( {P_{B}^{(i)} ,\;\theta_{B}^{(i)} } \right) \), the entire misorientation space (0 deg, 90 deg) can be divided into six distinct structural sets. These sets are delineated in Figure 2 by different colors. As we show next, STGBs belonging to different sets do not contain GBDs with the same Burgers vectors. Because of the fundamental differences in defect structure, a discontinuous change in STGB structure must occur as θ varies from one \( \left( {P_{B}^{(i)} ,\;\theta_{B}^{(i)} } \right) \) to an adjacent one \( \left( {P_{B}^{(j)} ,\;\theta_{B}^{(j)} } \right) \).

An analysis of the Burgers vectors of the GBDs b GB in the off-coherency STGBs is carried out using the topological models of References 1, 2, and 55–57. We find that the defect structure of these STGBs can be described by one of two possible tilt wall models, the type 1 in Figure 5(a) or type 2 in Figure 5(b). Representations of the same type 1 and type 2 tilt boundaries in terms of the perfect lattice vectors b A and b B of the adjoining crystals are shown in Figures 5(a’) and (b’), respectively. In these, the arrows indicate the direction of Burgers vectors. In both cases, the mean separation between dislocations follows Frank’s formula.[1,2,58]

$$ L = b/[ 2 {\text{ sin }}(\varphi / 2)\left] { \, = b_{\text{GB}} /} \right[ 2 {\text{ tan }}(\varphi / 2)] $$
(1)

where φ = 2 θ is the tilt angle, b is the perfect lattice Burgers length, and b GB is the grain boundary dislocation Burgers length. For the type 1 tilt boundary, the grain boundary Burgers vector is one half the sum of the two perfect lattice dislocations, b GB = (b A + b B)/2, i.e., b A = (b x , b y , b z ) = (bsinθ, bcosθ, 0), b B = (b x , b y , b z ) = (−bsinθ, bcosθ, 0), and thus, b GB = (0, bcosθ, 0). In this case, GBDs accommodate small rotations θ > 0 deg from the base structure plane by reorienting one P B plane, either above or below the GB plane, to align it with the GB plane, as illustrated in Figure 5(a’). The affected P B plane alternates between two consecutive GBDs to keep the boundary nominally flat, albeit with a slight rumple. For the type 2 tilt wall in Figure 5(b), b GB = (0, 2bcosθ, 0). The GBDs in a type 2 tilt wall correct the θ deviations from coherency by rotating the P B plane both above and below the GB plane to achieve coherency over large portions of the boundary. To accomplish this, b y of each GBD must produce a displacement of dcosΔθ normal to the boundary plane in both the top and bottom crystals, where d is the interplanar spacing of the P B plane, Δθ is the absolute difference between θ and θ B, and cosΔθ takes the projection of 2d normal to the GB plane. In other words, b y must sum to 2dcosΔθ, which is ~2d for Δθ within ±10 deg. Type 1 represents the lowest energy configuration when the formation energy of the P B plane is negligible and can be ignored. Type 2, in contrast, likely forms when the base boundary plane has the lower formation energy.

Fig. 5
figure 5

Tilt walls. (a) One formation mechanism of a tilt wall, and (a’) the corresponding tilt wall model, (b) the other formation mechanism of a tilt wall, and (b’) the corresponding tilt wall model. Burgers vectors b A and b B are perfect lattice vectors, and b GB is the Burgers vector of a grain boundary dislocation

Full size image

Using the preceding topological model, we find that a cluster of STGBs that deviate in θ more or less about the same special STGB (θ B, P B) and share the same P B are also found to have approximately the same b GB. Thus, STGBs belonging to the same set share a common P B base boundary structure and characteristic b GB. In all cases, the b GB does not correspond to a lattice dislocation belonging to the bulk crystal and has a component b y directed normal to the boundary plane (along the y direction in the MD model). Within each set, STGBs only vary in GBD spacing L and the sign of b GB. Significantly, \( [1\bar{2}10] \) STGBs can be classified in a similar fashion.[3]

In what follows, for each STGB, we report an average GBD spacing, calculated by simply dividing the periodic length in x (Px) by the number of GBDs N in each BUC, i.e., L = Px/N. This alternative definition is necessary because generally the spacing between adjacent GBDs within one periodic length along is nonuniform. This occurs in part because in the hcp crystal, the interplanar spacing between consecutive P B planes is not always equal, although the distribution of GBDs within different BUCs is the same.

5 Atomic Structures of \( [0\bar{1}10] \) STGBs

In this section, we describe the relaxed atomic structures of the simulated STGBs belonging to each of the six distinct structural sets. The results of these calculations are summarized in Table I for Mg and Table II for Ti.

Table I Structural Properties of \( [0\bar{1}10] \) Symmetrical Tilt Grain Boundaries in Mg: Rotation Angle θ (deg), the Average Spacing of Grain Boundary Dislocations\( < L > \) (nm), and the y Component of Burgers Vectors of Grain Boundary Dislocations, b y (nm)
Full size table
Table II Structural Properties of \( [0\bar{1}10] \) Symmetrical Tilt Grain Boundaries in Ti: Rotation Angle θ (deg), the Average Spacing of Grain Boundary Dislocations \( < L > \) (nm), and the y Component of Burgers Vectors of Grain Boundary Dislocations, b y (nm)
Full size table

The rotation angle and the spacing are measured from molecular dynamics simulations, and b y is calculated from Eq. [1].

The rotation angle and the spacing are measured from molecular dynamics simulations, and b y is calculated from Eq. [1].

5.1 Set 1 in Mg

Set 1 STGBs lie at the extreme low end of the θ range up to 24 deg (Table I), belong to type 1 tilt wall. The base structure \( P_{B}^{(1)} \) is the basal plane base structure and Burgers vector of GBDs follow \( \left| {b_{\text{y}} } \right| \, = c/ 2 {\text{ cos}}\theta \) (Figures 6(a) and (b)). Even as θ increases to 24 deg, these set 1 STGBs maintain an ordered atomic structure with no GBD core overlap. As θ increases above 24 deg, the STGB converts to a set 2 structure, which is discussed next.

Fig. 6
figure 6

Atomic structures of set 1 and set 6 in \( [0\bar{1}10] \) STGBs in Mg. (a) and (b) correspond to set 1 STGBs with θ = 15.1 deg and 22.1 deg; (c) and (d) correspond to set 6 STGBs with θ = 78.4 deg and 82.9 deg. Atoms are colored according their excess potential energy. The symbol “\( \bot \)” indicates the position and sign of grain boundary dislocation (Color figure online)

Full size image

5.2 Sets 2 to 5 in Mg

Sets 2 to 5 STGBs cover the wide range of intermediate rotation angles θ from 24 deg to 76 deg. Each set includes one of the four minimum-energy STGBs with \( P_{B}^{(2)} ,P_{B}^{(3)} P_{B}^{(4)} ,P_{B}^{(5)} \), and it belongs to the type 2 tilt wall. The θ range of each set is approximately ± 10 deg or less from the rotation angle θ B of the nearest minimum energy structure. For set 2 (Figures 7(a) through (c)), 24 deg < θ < 32 deg, the \( (\bar{2}116) \) boundary makes up the base coherent structure (Figure 7(b)), and \( \left| {b_{\text{y}} } \right| \, = \, 0. 30 4 {\text{ nm}} \). For set 3 (Figures 7(d) through (f)), 32 deg < θ < 48 deg, the \( (\bar{2}114) \) twin boundary forms the base structure (Figure 7(e)), and \( \left| {b_{\text{y}} } \right| \, = \, 0. 40 3 {\text{ nm}} \). For set 4 (Figures 8(a) through (c)), 48 deg < θ < 68 deg, the \( (\bar{2}112) \) twin boundary constitutes the base structure (Figure 8(b)), and \( \left| {b_{\text{y}} } \right| \, = \, 0. 5 4 3 {\text{ nm}} \). For set 5 (Figures 8(d) through (f)), 68 deg < θ < 76 deg, the \( (\bar{2}111) \) twin boundary represents the base structure (Figure 8(e)), and \( \left| {b_{\text{y}} } \right| \, = \, 0. 30 5 {\text{ nm}} \). A similar structural change in an imperfect STGB twin boundary was calculated via MD simulations by Fernandez et al.[12] for an asymmetric \( (\bar{2}112) \) TB, which was observed to consist of an array of edge GBDs separating coherent \( (\bar{2}112) \) twin regions. Moreover, the asymmetric \( (\bar{2}112) \) TB has the formation energy nearly three times higher than the symmetric \( (\bar{2}112) \) TB.

Fig. 7
figure 7

Atomic structures of set 2 and set 3 in \( [0\bar{1}10] \) STGBs in Mg. (a), (b), and (c) correspond to set 2 STGBs with θ = 24.9 deg, 28.4 deg, and 31.3 deg, respectively. (b) The \( (\bar{2}116) \) twin boundary is the base structure for STGBs in (a) and (c). (d), (e), and (f) correspond to set 3 STGBs with θ = 35.8 deg, 39.1 deg and 44.2 deg, respectively. (e) The \( (\bar{2}114) \) twin boundary is the base structure for STGBs in (d) and (f). Atoms are colored according their excess potential energy. The symbol “\( \bot \)” indicates the position and sign of grain boundary dislocation (Color figure online)

Full size image
Fig. 8
figure 8

Atomic structures of set 4 and set 5 in \( [0\bar{1}10] \) STGBs in Mg. (a), (b), and (c) correspond to set 4 STGBs with θ = 52.4 deg, 58.4 deg and 63.8 deg, respectively. (b) The \( (\bar{2}112) \) twin boundary is the base structure for STGBs in (a) and (c). (d), (e), and (f) correspond to set 5 STGBs with θ = 69.7 deg, 72.8 deg, and 75.2 deg, respectively. (e) The \( (\bar{2}111) \) twin boundary is the base structure for STGBs in (d) and (f). The atoms are colored according their excess potential energy. The symbol “\( \bot \)” indicates the position and sign of grain boundary dislocation (Color figure online)

Full size image

Set 2-5 STGBs are type 2 tilt walls (Figure 5(b)); thus, the GB plane may look like a twin plane. Figure 9 shows the y-z projection of several set 3 STGBs, clearly indicating that the twin plane acts as the base structure in these STGBs. Corresponding to the type 2 tilt wall, the Burgers vectors b y of the GBDs equal 2dcosΔθ, or approximately twice the interplanar spacing of the corresponding P B plane, because Δθ = (θ- θ B) tends to be at most ±10 deg. Accordingly, within a given set, the sign of b y switches from negative to positive as θ increases from below to above θ B. For the \( P_{B}^{(2)} ,P_{B}^{(3)} P_{B}^{(4)} ,P_{B}^{(5)} \) planes, respectively \( (\bar{2}116),\;(\bar{2}114),\;(\bar{2}112) \), and \( (\bar{2}111) \), the interplanar spacings d as a function of κ, the c/a ratio, are determined using Figure 3.

$$ d^{{(\bar{2}111)}} = \frac{c}{{\sqrt {1 + 4\kappa^{2} } }},\;d^{{(\bar{2}112)}} = \frac{c}{{\sqrt {1 + \kappa^{2} } }},\;d^{{(\bar{2}114)}} = \frac{c}{{\sqrt {4 + \kappa^{2} } }},\;d^{{(\bar{2}116)}} = \frac{c}{{\sqrt {9 + \kappa^{2} } }} $$
(2)
Fig. 9
figure 9

Atomic structures of set 3 in \( [0\bar{1}10] \) STGBs in the y-z projection: from the left to the right corresponding to θ = 34.8 deg, 35.8 deg, 39.1 deg, 42.8 deg, and 44.3 deg, respectively. The red line indicates the GB plane, showing that the \( (\bar{2}114) \) twin boundary plane acts as the base structure. The atoms are colored by their excess potential energy (Color figure online)

Full size image

From Eq. [2], two times the interplanar spacings for \( (\bar{2}116),\;(\bar{2}114),\;(\bar{2}112) \), and \( (\bar{2}111) \) in Mg are 0.304 nm, 0.403 nm, 0.543 nm, and 0.305 nm, respectively, which are equal to the \( \left| {b_{\text{y}} } \right| \) of sets 2, 3, 4, and 5, respectively, obtained from MD (Table I).

5.3 Set 6

At the other end of the spectrum lie the set 6 STGBs, representing the highest angle STGBs with tilts θ exceeding 76 deg (Figure 6(c) and (d)). STGBs in this set consist of an array of GBDs in a type 1 tilt wall configuration (see figure 5(a)). The base plane \( P_{B}^{(6)} \) in this case is the \( \left( {11\bar{2}0} \right) \) plane, which lies normal to the basal plane, θ B = 90 deg, and it intersects it along the \( [0\bar{1}10] \) axis. Achieving coherent P B regions between the GBDs requires that \( \left| {b_{\text{y}} } \right| \) is equal to the interplanar spacing of the \( \left( {11\bar{2}0} \right) \) plane, a/2, e.g., \( \left| {b_{\text{y}} } \right| \, = \, 0. 1 6 {\text{ nm}} \) for Mg (Table I).

5.4 Six Structural Sets for Ti

To test whether the MD results for Mg are applicable to other hcp c/a materials and other interatomic potentials, the calculations are repeated for STGBs in Ti (c/a = 1.5873) over the entire space of θ using the EAM potential for α-Ti.[52] We find that the same six structural sets develop with the same base structures as Mg. The calculated excess potential energy as a function of θ is plotted in Figure 10, with the misorientation ranges for the six structural sets indicated by different colors. As shown, four energy cusps arise at the same GB planes P B as in Mg: Four STGBs have tilts θ B = 27.9 deg, 38.4 deg, 57.8 deg, and 72.5 deg, and correspond to planes \( P_{\text{B}} = (\bar{2}116),\;(\bar{2}114),\;(\bar{2}112) \), and \( (\bar{2}111) \), respectively, and their formation energies vary substantially from 753.3 mJ/m2 and 815.4 mJ/m2 for \( (\bar{2}116) \) and \( (\bar{2}114) \) to 521.4 mJ/m2 and 519.1 mJ/m2 for \( (\bar{2}112) \) and \( (\bar{2}111) \). Regarding the misorientation range for each, the simulation finds that 0 deg < θ < 24 deg for set 1, 24 deg < θ < 34 deg for set 2, 34 deg < θ < 50 deg for set 3, 50 deg < θ < 63 deg for set 4, 63 deg < θ < 79 deg for set 5, and 79 deg < θ < 90 deg for set 6. The rotation angles, Burgers vectors, and GBD spacing for each simulated STGB in Ti are summarized in Table II.

Fig. 10
figure 10

Excess potential energies of \( [0\bar{1}10] \) STGBs in Ti as a function of θ. The colored regions mark six sets, S-1 to S-6, and their ranges of θ within which STGBs can be viewed as having similar atomic structure. S-1 and S-6: an array of GBDs; S-2 to S-5: minimum-energy boundaries plus an array of GBDs (Color figure online)

Full size image

To demonstrate the structural similarity with STGBs in Mg, we present a few examples of relaxed equilibrium structures of STGBs in Ti. Figure 11 shows the dislocation structures of some STGBs belonging to set 1 corresponding to angles θ = 6.95 deg, 9.01 deg and 12.8 deg. Figures 12 and 13 show the dislocation structures of some STGBs that are tilted off from the minimum-energy state. Figures 12(a) and (c) show set 4 STGBs with angles θ = 51.7 deg and 62.3 deg, respectively. Figure 12(b) (θ = 57.8 deg) is the \( (\bar{2}112) \) twin boundary acting as the base structure for STGBs in Figures 12(a) and (c). Set 5 STGBs with angles θ = 67.29 deg and 75.9 deg are shown in Figures 13(a) and (c), respectively, with a \( (\bar{2}111) \) twin boundary acting as their base structure (Figure 13(b)). The magnitude of Burgers vectors of GBDs presented in these STGBs are also calculated by using Eq. [1] with the input of the average spacings L between GBDs measured in MD simulations.

Fig. 11
figure 11

Atomic structures of set 1 in \( [0\bar{1}10] \) STGBs in Ti. (a), (b), and (c) correspond to the angle θ = 6.95 deg, 9.01 deg, and 12.8 deg, respectively. The atoms are colored according their excess potential energy. The symbol “\( \bot \)” indicates the position and sign of grain boundary dislocation (Color figure online)

Full size image
Fig. 12
figure 12

Atomic structures of set 4 in \( [0\bar{1}10] \) STGBs in Ti. (a), (b), and (c) correspond to the angle θ = 51.7 deg, 57.8 deg and 62.3 deg, respectively. (b) The \( (\bar{2}112) \) twin boundary is the base structure for STGBs in (a) and (c). The atoms are colored according their excess potential energy. The symbol “\( \bot \)” indicates the position and sign of grain boundary dislocation (Color figure online)

Full size image
Fig. 13
figure 13

Atomic structures of set 5 in \( [0\bar{1}10] \)STGBs in Ti. (a), (b), and (c) correspond to the angle θ = 67.2 deg, 72.5 deg, and 75.9 deg, respectively. (a) The \( (\bar{2}111) \) twin boundary is the base structure for STGBs in (b) and (c). The atoms are colored according their excess potential energy. The symbol “\( \bot \)” indicates the position and sign of grain boundary dislocation (Color figure online)

Full size image

6 hcp STGB Structure for General c/a

We have shown in Sections III through V that the defect structure of an STGB can be fully characterized once the structural set to which an STGB belongs is known. Every STGB containing GBDs lies within the misorientation range between two coherent (GBD-free) boundaries, which are either zero-energy or minimum-energy STGBs. Furthermore, each one belongs to a distinct structural set that derives its fundamental structure from one or the other one of its bounding neighboring boundaries. Thus, determining the structural set to which an STGB with a given rotation angle θ belongs translates to predicting the misorientation range \( \Updelta \theta^{{\left( {\text{i}} \right)}} = \left( {\theta_{L}^{(i)} ,\;\theta_{U}^{(i)} } \right) \) for each structural set i. A simple model to predict qualitatively the critical misorientations at which the STGB structure transitions from one set to another was introduced previously[3] and in this section, it is briefly reviewed and applied to treat the \( [0\bar{1}10] \) STGBs studied here.

The analytical model is based on the concept that the STGB structure that develops is the one with the lowest dislocation strain energy term, E/μ = ρb 2, where the GBD density ρ is approximately 1/L, b = \( \left| {b_{\text{y}} } \right| \), and μ is the shear modulus. As θ changes continuously, the STGB transitions to another structural set when accommodating larger deviations outside of Δθ (i) with the same base crystallographic plane \( P_{B}^{(i)} \) would require a larger multiple of \( b_{y}^{(i)} \) or much higher GBD density.

Let L (i) be the average GBD spacing for an STGB in set i. From Eq. [1], L (i)(θ) is

$$ L^{\left( i \right)} \left( \theta \right) \, = b_{y}^{(i)} / 2 {\text{sin}}(\theta - \theta_{B}^{(i)} ),i = { 1}, \ldots ,{ 6} $$
(3)

where L (i) is observed to increase to infinity as θ approaches θ B from greater or less than θ B. When the misorientation θ for a given STGB lies within = \( \left( {\theta_{L}^{(i)} ,\;\theta_{U}^{(i)} } \right) \), the GBD spacing is simply given by

$$ L\left( \theta \right) \, = L^{(i)} (\theta ),\;\theta \in (\theta_{L}^{(i)} ,\theta_{U}^{(i)} ) $$
(4)

The lower limit \( \theta_{L}^{(i)} \) is defined by equality between [ρb 2(θ)](i−1) and [ρb 2(θ)](i)

$$ \theta_{L}^{(i)} = \theta \;{\text{s}}.{\text{t}}. \, \left[ {\rho b^{ 2} \left( \theta \right)} \right]^{(i - 1)} = \, \left[ {\rho b^{ 2} \left( \theta \right)} \right]^{(i)} $$
(5)

and the upper limit \( \theta_{U}^{(i)} \), given when [ρb 2(θ)](i+1), is equal to [ρb 2(θ)](i)

$$ \theta_{U}^{(i)} = \theta \;{\text{s}}.{\text{t}}. \, \left[ {\rho b^{ 2} \left( \theta \right)\left] {^{(i + 1)} = \, } \right[\rho b^{ 2} \left( \theta \right)} \right]^{(i)} $$
(6)

This model is simple in that it neglects GBD interaction energies, base structure formation energies, and GBD core energies. Consequently, the model outlined previously can be expected at best to forecast the structure to first order.

The angle \( \theta_{B}^{(i)} \) and \( b_{y}^{(i)} \) for each set i are related to the corresponding base structure \( P_{B}^{(i)} \). Given the Miller-Bravais index {uviw} for the crystallographic plane \( P_{B}^{(i)} \) and the κ = c/a ratio for the hcp material of interest, \( \theta_{B}^{(i)} \) is given by

$$ \theta_{B} = \cos^{ - 1} \left[ {\frac{3w/2}{{\sqrt {3\kappa^{2} (u^{2} + uv + v^{2} ) + 9w^{2} /4} }}} \right] $$
(7)

Sets 1 and 6 STGBs adopt a type 1 tilt configuration (Figure 5(a)), and thus, b y is equal to or nearly equal to the interplanar spacing d of \( P_{B}^{(i)} \), i.e.

$$ b_{y}^{(1)} = c\,{ \cos }\,\theta / 2= d\,{ \cos }\,\theta \quad {\text{when}}\;P_{B}^{(1)} = \, \left( {000 2} \right) $$
(8)

or

$$ b_{y}^{(6)} = a/ 2 { } = d\quad {\text{when}}\;P_{B}^{(6)} = \left( {11\bar{2}0} \right) $$
(9)

Sets 2 through 5 STGBs adopt a type 2 tilt structure (Figure 5(b)). In these cases, P B is a pyramidal plane, e.g., \( (\bar{2}112),\;(\bar{2}116) \), and b y is approximately twice d

$$ b_{y}^{(i)} = 2d^{\left( i \right)} { \cos }\Updelta \theta $$
(10)

where d (i) is given in Eq. [2].

The model equations (Eqs. [3] through [10]) require identifying first the base structures \( P_{B}^{(i)} \), which are given by boundary energy vs θ plots such as in Figures 2 and 10. These boundaries are favorable energetically, including trivially the zero-energy states of a perfect crystal and nontrivially the local minima in formation energy with respect to θ. These are coherent boundaries that correspond not only to twin boundaries observed experimentally. It should be noted that some coherent STGBs are not associated with local minima in this curve.

In Table III, we report the misorientation ranges Δθ (i) for Mg, Zr, Ti, and Zn, assuming the \( [0\bar{1}10] \) STGBs of these metals possess the same set of minimum-energy boundaries.

Table III Model Predictions for the Misorientation Range (to nearest 1 deg) and the y Component of Burgers Vectors of Grain Boundary Dislocations, b y (nm), for \( [0\bar{1}10] \) Symmetrical Tilt Grain Boundaries in Mg, Ti, Zr, and Zn
Full size table

Despite simplifying assumptions, the misorientation ranges provided by the model for Mg and Ti are in reasonable agreement with MD simulations and experimental measurements for most of the misorientation range. Significantly, the current MD simulations show and the model proves that the Δθ (i) for hcp STGBs is unrelated to the critical rotation angle that leads to GBD core overlap. The most noticeable consequence of neglecting the other energetic terms in the model is the underestimate of \( \theta_{U}^{(1)} = \theta_{L}^{(2)} \). Equations [5] and [6] predict that the limit \( \theta_{U}^{(1)} = \theta_{L}^{(2)} \) is ~15 deg to 17 deg for both Mg and Ti, which would correspond to a very small GBD spacing (ranging between b y and c) for a set 2 STGB with θ slightly above \( \theta_{L}^{(2)} \). MD calculations show that the set 1/set 2 transition actually occurs at a much higher misorientation angle, ~24 deg to 28 deg, and the GBD spacing in the newly transformed set 2 STGB is much wider, nearly 2c to 4c. Apparently, it is more energetically favorable to have an array of closely spaced GBDs than an array of more widely spaced GBDs with Burgers vectors approximately twice as large. Last, it is worth mentioning that Komninou et al.[43] observed an array varying in spacing from 4 to 8 nm in a \( (\bar{2}112) \) TB rotated a few degrees off ideal in Ti. According to our model, a ±2 deg deviation would lead to GBDs spaced 7.15 nm apart in a \( (\bar{2}112) \) TB in Ti (Table II), which is in good agreement with the reported data.

Note that both the rotation angles corresponding to the high-energy coherent \( (\bar{2}115) \) STGB (θ B = 33 deg) and \( (\bar{2}113) \) STGB (θ B = 47.26 deg) lie near the estimated \( \theta_{U}^{(1)} = \theta_{L}^{(2)} \) and \( \theta_{U}^{(2)} \), respectively. Thus, at these misorientations, set 1 and set 2 STGBs boundaries consisting of an array of GBDs are energetically preferred over these two coherent STGBs.

7 Conclusions

In this work, we use atomistic simulations and interfacial defect theory to examine the atomic structure of STGBs in hcp crystals with a \( [0\bar{1}10] \) tilt axis. Both Mg and Ti were studied and for both metals, the following conclusions apply:

  1. 1.

    All \( [0\bar{1}10] \) STGBs studied here have an ordered atomic structure containing either no intrinsic grain boundary dislocations (GBDs) or an array of discrete and distinct GBDs oriented along the tilt axis.

  2. 2.

    For Mg and Ti, not all possible coherent \( [0\bar{1}10] \)STGBs are observed; only four manifest as minimum-energy coherent (GBD free) STGBs:\( (\bar{2}111),\;(\bar{2}112),\;(\bar{2}114) \), and \( (\bar{2}116) \). These four STGBs, in addition to the two zero-energy boundaries corresponding to a perfect crystal: the (0001) basal plane at θ = 0 deg and \( \left( {11\bar{2}0} \right) \) plane at θ = 90 deg, give rise to six special boundaries, with GB plane and rotation angle denoted as \( \left( {P_{B}^{(i)} ,\;\theta_{B}^{(i)} } \right),\;i = { 1}, \ldots ,{ 6} \).

  3. 3.

    \( [0\bar{1}10] \)STGBs that deviate from one of these six special boundaries can be described as a tilt wall containing a single array of GBDs oriented along the tilt axis.

  4. 4.

    Like \( < 1\bar{2}10 > \) STGBs,[3] every \( [0\bar{1}10] \)STGB with a given θ falls into one of six distinct structural sets i, i = 1, …, 6. The misorientation range of set i, \( \Updelta \theta^{{\left( {\text{i}} \right)}} = \left( {\theta_{L}^{(i)} ,\;\theta_{U}^{(i)} } \right) \) is more or less centered about its special boundary \( \left( {P_{B}^{(i)} ,\;\theta_{B}^{(i)} } \right) \). STGBs within each set possess an ordered structure with \( P_{B}^{(i)} \) serving as the base plane, share the same characteristic \( b_{y}^{(i)} \), and only vary in GBD spacing as θ tilts away from \( \theta_{B}^{(i)} \).

  5. 5.

    Sets 1 (low angle) and 6 (high angle) have a type 1 tilt wall configuration and the magnitude of the GBD Burgers vector approximately equals one interplanar spacing of this plane.

  6. 6.

    Sets 2 through 5 (intermediate angles) are associated with one of the four local minimum-energy, coherent STGBs. STGBs tilted off from one of these four are type 2 tilt boundaries containing GBDs, whose magnitude is approximately two times the interplanar spacing of P B.

  7. 7.

    Within each set, the array spacing and sign of GBDs varies with θ, as expected from Frank’s formula.[58]

  8. 8.

    A simple model for the misorientation range of each set is employed to forecast the structures of other c/a hcp metals and shown to achieve reasonable agreement with MD simulation and experimental data in the literature.

It will be important in the future to test whether the structural sets discovered for \( [0\bar{1}10] \) STGBs translate directly with reaction groups, wherein two STGBs belonging to the same structural set respond in the same way to incoming lattice dislocations or other defects.[59] Studies of the kinetics and energetics underlying particular dislocation/boundary interactions such as slip or twin transmission across boundaries[60–62] and slip or twin nucleation from boundaries[59,63–65] are particularly important in developing atomistically informed and, hence, more reliable mesoscale dislocation dynamics approaches; see, for example, References 65 and 66.