Lifted system framework for learning control with different trial lengths

Abstract

This paper addresses an iterative learning control (ILC) design problem for discrete-time linear systems with randomly varying trial lengths. Due to the variation of the trial lengths, a stochastic matrix and an iteration-average operator are introduced to present a unified expression of ILC scheme. By using the framework of lifted system, the learning convergence condition of ILC in mathematical expectation is derived without using λ-norm. It is shown that the requirement on classic ILC that all trial lengths must be identical is mitigated and the identical initialization condition can be also removed. In the end, two illustrative examples are presented to demonstrate the performance and the effectiveness of the proposed ILC scheme for both time-invariant and time-varying linear systems.

1 Introduction

Iterative learning control (ILC), as an effective control strategy, was initially proposed in 1984[1]. Although it has been well established in terms of both the underlying theory and experimental applications[2–18], there are still several limitations in traditional ILC that every trial (pass, cycle and iteration) must end in a fixed duration, and that the initial state of the objective system must be set to the same point at the beginning of each iteration, etc. In many applications of ILC, nevertheless, it would not be the case that every trial ends in a fixed duration. For instance, as introduced in [19], when stroke patients walk on a treadmill, depending on their strength and abilities, the steps will be usually cut short by suddenly putting the foot down. Assuming that up to this point, the movement of hip and knee was hardly different from the movement in a full-length step, the data gathered in these aborted steps should be used for learning under the framework of ILC. Similarly, as demonstrated in [20], the gaits problems of humanoid robots are divided into phases defined by foot strike times, where the durations of the phases are usually not the same from cycle to cycle during the learning process. Thus, when ILC is applied, the non-uniform trial length problem occurs. One more example is the timing belt drive system that might be used in a copy machine[20]. When the velocity of output shaft varies, the period of rotation changes accordingly due to the inaccuracies of gearing, thus also hinders the application of classic ILC schemes.

In existing literature, there are some works investigating the ILC design problems for systems with non-uniform trial lengths. In [21], a non-standard ILC approach is developed for the systems operating continuously in time. The ILC algorithm was applied by defining a “trial” in terms of completion of a single “period” of the output trajectory, where the actual trial length will likely be different from the desired trial length. In [19], monotonic convergence of linear ILC systems with varying pass length is considered by using the lifting method. While in [19, 20], the identical initialization condition is one of the fundamental requirements for their controller design. Recently, ILC problem for discrete-time linear systems with randomly varying trial lengths is investigated in [22], where an ILC scheme based on the iteration-average operator is proposed. By introducing a stochastic variable satisfying Bernoulli distribution, a unified expression of ILC scheme is given for systems with different trial lengths and the convergence of tracking error is finally derived in the sense of mathematical expectation. In addition, the identical initialization condition is removed. It is well known that most of convergence analysis of ILC are based on λ-norm which sometimes hinders the applicability of ILC in practice[23–25]. In this work, in order to avoid using the λ-norm, we reformulate the ILC design problem with randomly varying trial lengths under the framework of lifted systems. By introducing a stochastic matrix and an iteration-average operator, a unified expression of ILC scheme is proposed and the convergence condition of tracking error in mathematical expectation is given for both time-invariant and time-varying linear systems.

The main contributions of the paper are summarized as follows:

• 1) A new formulation is presented for ILC of discrete-time systems with randomly varying trial lengths by defining a stochastic matrix. Comparing with [22], the introduction of the stochastic matrix is more straightforward, and the calculation of its probability distribution is less complex.

• 2) Different from [22], we investigate ILC for systems with non-uniform trial lengths under the framework of lifted system and the utilization of λ-norm is avoided.

• 3) Instead of being confined to the identical initialization condition as in [19, 20], the initial states could be randomly varying.

The rest of the paper is organized as follows. Section 2 formulates the ILC problems with randomly varying trial lengths. In Section 3, controller design and convergence analysis are presented. Further, the proposed ILC law is extended to time-varying systems in Section 4. Section 5 gives two illustrative examples. Throughout this paper, ∥·∥ denotes the Euclidean norm or any consistent norm. ${\cal N}$ denotes the set of natural numbers, and I is the identity matrix. Moreover, define ${{\cal I}_d} \buildrel \Delta \over = \{1,2, \cdots ,{T_d}\}$, where T _d is the desired trial length, and ${{\cal I}_i} \buildrel \Delta \over = \{1,2, \cdots ,{T_i}\}$, where ${T_i},i \in {\cal N}$ is the trial length of the i-th iteration. When T _i < T _d , it follows that ${{\cal I}_i} \subset {{\cal I}_d}$. We define ${{\cal I}_d}/{{\cal I}_i} \buildrel \Delta \over = \{t \in {{\cal I}_d}:t \notin {{\cal I}_i}\}$ as the complementary set of ${{\cal I}_i}$ in ${{\cal I}_d}$. We give two integers N₁ and N ₂ satisfying 0 ≤ N₁ < T _d and N₂ ≥ 0, respectively. Set ${{\cal I}_N} \buildrel \Delta \over = \{1,2, \cdots ,{T_d} - {N_1},{T_d} - {N_1} + 1, \cdots ,{T_d} + {N_2}\}$ and it may be divided into two subsets: ${{\cal I}_a} \buildrel \Delta \over = \{1,2, \cdots ,{T_d} - {N_1} - 1\}$ and ${{\cal I}_b} \buildrel \Delta \over = \{{T_d} - {N_1},{T_d} - {N_1} + 1, \cdots ,{T_d} + {N_2}\}$. ${{\cal I}_a}$ is the set that is not affected by the randomly varying factor, whereas ${{\cal I}_b}$ is the set that accounts for the randomly varying duration. Define ${\tau _m} \buildrel \Delta \over = {T_d} - {N_1} + m,m \in \{0,1, \cdots ,{N_1} + {N_2}\}$, which implies ${\tau _m} \in {{\cal I}_b}$.

2 Problem formulation

Consider a class of linear discrete-time systems

$$\left\{{\matrix{{{x_i}(k + 1) = A{x_i}(k) + B{u_i}(k)} \hfill \cr{{y_i}(k) = C{x_i}(k)} \hfill \cr}} \right.$$

(1)

where k ∈ {0, 1, 2,⋯, T _i } denotes discrete time. Meanwhile, x _i (k) ∈ Rⁿ, u _i (k) ∈ R and y _i (k) ∈ R denote state, input and output of the system (1), respectively. Further, A, B and C are constant matrices with appropriate dimensions, and CB ≠ 0. This state-space system is equivalent to

$${y_i}(k) = \underbrace {C{{(qI - A)}^{- 1}}B}_{P(q)}{u_i}(k) + \underbrace {C{A^k}{x_i}(0)}_{{d_i}(k)},\;\;k \in {{\cal I}_i}$$

(2)

where q is the forward time-shift operator qx(k) = x(k +1). This system can be written equivalently as the T _i × T _i -dimensional lifted system:

$$\left[ {\begin{array}{*{20}c} {y_i (1)} \\ {y_i (2)} \\ \vdots \\ {y_i (T_i )} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {p_1 } & 0 & \cdots & 0 \\ {p_2 } & {p_1 } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {pT_i } & {pT_i - 1} & \cdots & {p_1 } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {u_i (0)} \\ {u_i (1)} \\ \vdots \\ {u_i (T_i - 1)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {d_i (1)} \\ {d_i (2)} \\ \vdots \\ {d_i (T_i )} \\ \end{array} } \right]$$

(3)

where ${p_k}| = C{A^{k - 1}}B,k \in {{\cal I}_i}$, are Markov parameters.

Let yd(k), k ∈ {0, 1, 2,⋯, T _d } be the desired output trajectory. Assume that, for any realizable output trajectory yd(k), there exists a unique control input ud(k) such that

$$\left\{ {\begin{array}{*{20}c} {x_d (k + 1) = Ax_d (k) + Bu_d (k)} \\ {y_d (k) = Cx_d (k).} \\ \end{array} } \right.$$

(4)

In addition, system (4) can be rewritten as

(5)

where ${d_d}(k) = C{A^k}xd(0),k \in {{\cal I}_d}$.

The main difficulty in designing ILC scheme for the system (1) is that the actual trial length T _i is iteration-varying and different from the desired trial length T _d .

Before addressing the ILC design problem with nonuniform trial lengths, let us give some notations and assumptions that would be useful in the derivation of our main result.

• Definition 1. E(f) stands for the mathematical expectation of the stochastic variable f. P[f] means the occurrence probability of the event f.

• Assumption 1. Assume that ${T_i} \in {{\cal I}_b}$ is a stochastic variable with $P[{T_i} = {\tau _m}] = {q_m},{\tau _m} \in {{\cal I}_b}$, where 0 ≤ q _m < 1 is a known constant.

• Assumption 2. E(x _i (0)) = x _d (0).

• Remark 1. The contraction mapping based ILC usually requires the identical initial condition in each iteration. In Assumption 2, the condition is extended clearly. The initial states of system could change randomly with E(x _i (0)) = x _d (0) and there are no limitations to the variance of x _i (0).

If the control process (1) repeats with the same trial length T _d , i.e., T _i = T _d , and under the identical initial condition, a simple and effective ILC[26] for the linear system (1) is

$${U_{i + 1}} = {U_i} + L{e_i}$$

(6)

where ${U_i} \buildrel \Delta \over = {[{u_i}(0),{u_i},(1), \cdots ,{u_i}({T_d} - 1)]^{\rm{T}}}$, L is an appropriate learning gain matrix, and the tracking error is defined as

$$\underbrace {\left[ {\matrix{{{e_i}(1)} \cr{{e_i}(2)} \cr\vdots \cr{{e_i}({T_d})} \cr}} \right]}_{{e_i}} \buildrel \Delta \over = \underbrace {\left[ {\matrix{{{y_d}(1)} \cr{{y_d}(2)} \cr\vdots \cr{{y_d}({T_d})} \cr}} \right]}_{{Y_d}} - \underbrace {\left[ {\matrix{{{y_i}(1)} \cr{{y_i}(2)} \cr\vdots \cr{{y_i}({T_d})} \cr}} \right]}_{{Y_i}}.$$

(7)

However, when the trial length T _i is iteration-varying, which corresponds to a non-standard ILC process, the learning control scheme (6) has to be re-designed.

3 ILC design and convergence analysis

In this section, based on the assumptions and notations that are given in Section 2, ILC design and convergence analysis are addressed, respectively.

In practice, for one scenario that the i-th trial ends before the desired trial length, i.e., T _i < T _d , both the output y _i (k) and the tracking error e _i (k) on the time interval ${{\cal I}_d}/{{\cal I}_i}$ are missing, i.e., unavailable for learning. For the other scenario that the i-th trial is still running after the time instant we want it to stop, i.e., T _i > T _d , the signals y _i (k)and e _i (k) after the time instant T _d are redundant and useless for learning. In order to cope with those missing signals or redundant signals in different scenarios, we define a stochastic matrix. By using the stochastic variables, a newly defined tracking error $e_i^*$ is introduced to facilitate the modified ILC design.

The main procedure for deriving a modified ILC scheme can be described as follows:

• 1) Define a stochastic matrix Γ _i .

  Let Γ _i be a stochastic matrix with possible values

  $$D({\tau _m}) \buildrel \Delta \over = \left\{{\matrix{{{\rm{diag}}\overbrace {{\rm{\{}}\underbrace {{\rm{1,}} \cdots {\rm{,1}}}_{{\tau _m}},0, \cdots ,0\}}^{{T_d}},\quad {\tau _m} < {T_D}} \hfill \cr{{I_{{T_d} \times {T_d},}}\quad {\tau _m} \times {T_d}.} \hfill \cr}} \right.$$

  (8)

  The relationship Γ _i = D(τ _m ) represents the event that the i-th trial length of control process (1) is τ _m , which occurs with a probability of q _m , where 0 <q _m ≤ 1, is a prespecified constant as shown in Assumption 1.

• 2) Compute the mathematical expectation E(Γ _i ).

  The mathematical expectation of the stochastic matrix Γ _i is

  $$\matrix{{{\rm{E(}}{\Gamma _i}{\rm{) =}}\sum\limits_{m = 0}^{{N_1} + {N_2}} {D({\tau _m})} {q_m} =} \hfill \cr{\quad \sum\limits_{m = 0}^{{N_1} - 1} {D({\tau _m}){q_m} + {I_{{T_d} \times {T_d}}}(\sum\limits_{m = {N_1}}^{{N_1} + {N_2}} {{q_m}}) =}} \hfill \cr{\quad {\rm{diag\{}}\underbrace {{\rm{1,1,}} \cdots {\rm{,1}}}_{{T_d} - {N_1}},\sum\limits_{m = 1}^{{N_1} + {N_2}} {{q_m}, \cdots ,\sum\limits_{m = {N_1}}^{{N_1} + {N_2}} {{q_m}\} \buildrel \Delta \over = \overline D .}}} \hfill \cr}$$

  (9)

• 3) Define a modified tracking error. Denote

  $$e_i^{\ast} \buildrel \Delta \over = {\Gamma _i}{e_i}$$

  (10)

  as a modified tracking error, which renders to

  $$e_i^* = \left\{ {\begin{array}{*{20}c} {\left[ {e_i (1), \cdots ,e_i \left( {T_i } \right),0, \cdots ,0} \right]^T ,} & {T_i < T_d } \\ {e_i ,} & {T_i \geqslant T_d .} \\ \end{array} } \right.$$

  (11)

  • Remark 2. Since the absent signals are unavailable, and the redundant signals are useless for learning, it is reasonable to define a modified tracking error $e_i^*$ as in (11) or equivalently (10). In the modified tracking error $e_i^*$, the redundant signals are cut off when T _i > T _d , and the unavailable signals are set as zero when T _i < T _d .

• 4) The modified ILC scheme.

Introduce an iteration-average operator A(·)[14] as

$$A({f_i})(\cdot)) \buildrel \Delta \over = {1 \over {i + 1}}\sum\limits_{j = 0}^i {{f_j}(\cdot)}$$

(12)

for a sequence f₀ (·), f₁(·), ⋯, f _i (·), which plays a pivotal role in the proposed controller. The modified ILC scheme is given as

$${U_{i + 1}} = A({U_i}) + {{i + 2} \over {i + 1}}L\sum\limits_{j = 0}^i {e_j^{\ast}}$$

(13)

for all $i \in {\cal N}$, where the learning gain matrix L will be determined in the following.

Theorem 1 presents the first main result of the paper.

• Theorem 1. For the discrete-time linear system (1) and the ILC scheme (13), choose the learning gain matrix L such that, for any constant 0 ≤ ρ < 1,

  $$\mathop {\sup}\limits_{k \in {{\cal I}_d}} \left\Vert {I - L\overline D P} \right\Vert \leq \rho$$

  (14)

  then the mathematical expectation of the error, ${\rm{E}}({e_i}(k)),k \in {{\cal I}_d}$, will converge to zero asymptotically as i → ∞.

• Remark 3. In practice, the probability distribution of the trial length T _i could be estimated in advance based on previous multiple experiments or by experience. In consequence, the probability q _m in Assumption 1 is known. Finally, $\bar D$ can be calculated by (9), thus is available for controller design.

• Proof. The proof consists of two parts. Part 1 proves the convergence of the input error in iteration-average and mathematical expectation by using contraction mapping. Part 2 proves the convergence of the tracking error in mathematical expectation.

• Part 1. Let ΔU _i ≜ U _d − U _i be the input error. By the definition of iteration-average operator (12), we can rewrite A(ΔU _i + 1)as

  $$A(\Delta {U_{i + 1}}) = {1 \over {i + 2}}[\Delta {U_{i + 1}} + (i + 1)A\{\Delta {U_i}\} ].$$

  (15)

  In addition, subtracting U _d from both sides of the ILC law (13), we have

  $$\Delta {U_{i + 1}} = A(\Delta {U_i}) - {{i + 2} \over {i + 1}}L\sum\limits_{j = 0}^i {e_j^{\ast}} .$$

  (16)

  Then, substituting (16) into the right hand side of (15) and applying the operator E{·} on both sides of (15), we obtain

  $$E(A(\Delta {U_{i + 1}})) = E(A(\Delta {U_i})) - L{\rm{E}}(A(e_i^{\ast})).$$

  (17)

  Since both E(·) and A(·) are linear operators, we can exchange the operation orders of E(·)and A(·), which yields

  $$E(A(e_i^{\ast})) = \overline D {\rm{E}}(A({e_i}))$$

  (18)

  where ${\rm{E}}({\Gamma _j}{e_j}) = \bar D{\rm{E}}({e_j})$ is applied as Γ _j and e _j are independent from each other. Meanwhile, from (3), (5) and (7), it follows that

  $${e_i} = P\Delta {U_i} + ({d_d}{\rm{-}}{d_i})$$

  (19)

  where d _i ≜ [d _i (1), d _i (2), ⋯, d _i (T _d )]^T. Then, combining (18) and (19) gives

  $$E(A(e_i^{\ast})) = \overline D P{\rm{E(}}A(\Delta {U_i})) + \overline D {\rm{E(}}A({d_d} - {d_i})).$$

  (20)

  By virtue of Assumption 2, we can obtain that

  $${\rm{E}}({d_d} - {d_i}) = {\rm{E(}}{d_d}) - {\rm{E(}}{d_i}{\rm{) = 0}}$$

  (21)

  which yields

  $${\rm{E}}(A({d_d} - {d_i}) = {\rm{0}}.$$

  (22)

  Then, the relationship (20) becomes

  $${\rm{E}}(A(e_i^{\ast})) = \overline D P{\rm{E(}}A(\Delta {U_i})).$$

  (23)

In consequence, substituting (23) into (17), we have

$${\rm{E}}(A(\Delta {U_{i + 1}})) = [I - L\overline D P]{\rm{E(}}A(\Delta {U_i})).$$

(24)

Taking the norm ∥·∥ on both sides leads to

$$\matrix{{\left\Vert {E(A(\Delta {U_{i + 1}}))} \right\Vert \leq} \hfill \cr{\quad \left\Vert {I - L\overline D P} \right\Vert \left\Vert {{\rm{E(}}A(\Delta {U_i}))} \right\Vert \leq} \hfill \cr{\quad \rho \left\Vert {E(A(\Delta {U_i}))} \right\Vert .} \hfill \cr}$$

(25)

According to the condition (14) and 0 ≤ ρ < 1, (25) implies that

$$\mathop {\lim}\limits_{i \rightarrow \infty} \Vert {{\rm{E}}(A(\Delta {U_i}))} \Vert = 0.$$

(26)

• Part 2. Now we prove the convergence of e _i in mathematical expectation. Multiplying both sides of (25) by (i + 2), it follows that

  $$\Vert {{\rm{E}}(\sum\limits_{j = 0}^{i + 1} {\Delta {U_j}})} \Vert \leq \rho \Vert {{\rm{E}}(\sum\limits_{j = 0}^i {\Delta {U_j}})} \Vert + \rho \Vert {{\rm{E}}(A(\Delta {U_i}))} \Vert .$$

  (27)

  According to the boundedness of ∥E(A(ΔU _i ))∥ from (25), (26) and Lemma 1 in [14], we can further derive ${\lim _{i \to \infty}}E(\sum _{j = 0}^i{U_j}) = 0$, thus

  $$\mathop {\lim}\limits_{i \rightarrow \infty} E(\Delta {U_i}) = \mathop {\lim}\limits_{i \rightarrow \infty} [E(\sum\limits_{j = 0}^i {\Delta {U_j}) - {\rm{E}}(\sum\limits_{j = 0}^{i - 1} {\Delta {U_j})] = 0.}}$$

  (28)

  Applying the operator E(·) on both sides of (19) yields

  $$E({e_i}) = P{\rm{E}}(\Delta {U_i})$$

  (29)

  where Assumption 2 is applied. Finally, it is proved that lim _i →∞ E(e _i )=0. □

• Remark 4. In Assumption 1, it is assumed that the probability distribution is known and then the mathematical expectation matrix $\bar D$ can be calculated directly. Whereas, if q _m is unknown, we know its lower and upper bounds, i.e., 0 ≤ α₁ ≤ q _m ≤ α₂ ≤ 1(α₁ and α₂ are known constants), then, according to (9), we have

  $$\matrix{{{\rm{diag\{}}\underbrace {{\rm{1,1,}} \cdots {\rm{,1}}}_{{T_d} - {N_1}},({N_1} + {N_2}){\alpha _1}, \cdots ,({N_2} + 1){\alpha _1}\} \leq} \hfill \cr{\quad \quad \overline D \leq {\rm{diag\{}}\underbrace {{\rm{1,1,}} \cdots {\rm{,1}}}_{{T_d} - {N_1}},({N_1} + {N_2}){\alpha _2}, \cdots ,({N_2} + 1){\alpha _2}\}} \hfill \cr}$$

  where “≤” means that every corresponding diagonal element of the left matrix is less than that of the right one. Based on the lower and upper bounds of $\bar D$ and convergence condition (14), the controller can be designed similarly.

4 Extension to time-varying systems

In this section, the proposed ILC scheme is extended to time-varying systems

$$\left\{{\matrix{{{x_i}(k + 1) = A(k){x_i}(k) + B(k){u_i}(k)} \hfill \cr{{y_i}(k) = C(k){x_i}(k)} \hfill \cr}} \right.$$

(30)

where A(k), B(k) and C(k) are time-varying matrices with appropriate dimensions and C(k)B(k) =0. This system can be written equivalently as the T _i × T _i -dimensional lifted system as

$$\left[ {\matrix{{{y_i}(1)} \cr{{y_i}(2)} \cr\vdots \cr{{y_i}({T_i})} \cr}} \right] = {P_i}\left[ {\matrix{{{u_i}(0)} \cr{{u_i}(1)} \cr\vdots \cr{{u_i}({T_i} - 1)} \cr}} \right] + \left[ {\matrix{{{w_i}(1)} \cr{{w_i}(2)} \cr\vdots \cr{{w_i}({T_i})} \cr}} \right]$$

(31)

where ${w_i}(k) = C(k)\prod _{j = 0}^{k - 1}A(j){x_i}(0)$ and

$$P_i = \left[ {\begin{array}{*{20}c} {C(1)B(0)} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ {C(T_i )\prod\limits_{k = 1}^{T_i - 1} {A(k)B(0)} } & \cdots & {C(T_i )B(T_i - 1)} \\ \end{array} } \right].$$

The desired trajectory Y _d is generated by

$${Y_d} = P{U_d} + {d_d}$$

(32)

where

$$P = \left[ {\begin{array}{*{20}c} {C(1)B(0)} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ {C(T_d )\prod\limits_{k = 1}^{T_d - 1} {A(k)B(0)} } & \cdots & {C(T_d )B(T_d - 1)} \\ \end{array} } \right]$$

The result is summarized in the following theorem.

• Theorem 2. For the discrete-time linear time-varying system (30) and the ILC algorithm (13), we choose the learning gain matrix L such that, for any constant 0 ≤ ρ < 1,

  $$\mathop {\sup}\limits_{k \in {{\cal I}_d}} \Vert {I - L(k)\overline D P} \Vert \leq \rho$$

  (33)

  the mathematical expectation of the error, ${\rm{E}}({e_i}(k)),k \in {{\cal I}_d}$, will converge to zero asymptotically as i → ∞.

• Proof. The proof can be performed similarly as in the proof of Theorem 1.

Considering the desired dynamics and the lifted system (31), we have

$${e_i} = P\Delta {U_i} + ({d_d} - {w_i})$$

(34)

where w _i ≜ [w _i (1), w _i (2),⋯, w _i (T _d )]^T. Similar as (20)–(23), it follows that

$${\rm{E}}(A(\Delta {U_{i + 1}})) = [I - L\overline D P]{\rm{E}}(A(\Delta {U_i})).$$

(35)

Now, following the procedure of the proof of Theorem 1, we can conclude that lim_i→∞ E(e _i )= 0. □

• Remark 5. In Theorems 1 and 2, the identical initialization condition is replaced by E(x _i (0)) = x _d (0). So, other than deriving the convergence of tracking error, we prove its mathematical expectation converges asymptotically by using the mathematical expectation operator and the proposed iteration-average based ILC scheme.

5 Illustrative example

In order to show the effectiveness of the proposed ILC scheme, two examples are considered.

• Example 1. Time-invariant system.

Consider the following discrete-time linear time-invariant system

$$\begin{array}{*{20}c} {x_i (k + 1) = \left( {\begin{array}{*{20}c} {0.50} & 0 & {1.00} \\ {0.15} & {0.30} & 0 \\ { - 0.75} & {0.25} & { - 0.25} \\ \end{array} } \right)} \\ {y_i (k) = \left( {\begin{array}{*{20}c} 0 & 0 & {1.00} \\ \end{array} } \right)x_i (k)} \\ \end{array} x_i (k) + \left( {\begin{array}{*{20}c} 0 \\ 0 \\ {1.00} \\ \end{array} } \right)u_i (k)$$

(36)

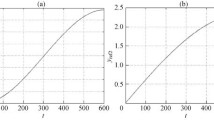
where ${x_i}(0) = {[0,0,0]^{\rm{T}}},i \in {\cal N}$. Let the desired trajectory be ${y_d}(k) = \sin ({{2\pi k} \over 5}) + \sin ({{2\pi k} \over 5}) + \sin (50\pi k),k \in {{\cal I}_d} \buildrel \Delta \over = \{1,2, \cdots ,50\}$, as shown in Fig. 1, and thus, T _d = 50. Without loss of generality, set ${u_0}(k) = 0,k \in {{\cal I}_d}$ in the first iteration. Moreover, assume that N₁ = N₂ =5and that T _i is a stochastic variable satisfying discrete uniform distribution. Then, T _i ∈ {45, 46, ⋯, 55} and $P[{T_i} = {\tau _m}] = {1 \over {11}}$, where τ _m =45 + m, m ∈ {0, 1, ⋯, 10}. Further, the learning gain is set as L = 0.5I_50×50. The performance of the tracking error ∥e _i ∥ is presented in Fig. 2. It shows that the tracking error ∥e _i ∥ will converge within 42 iterations.

Fig. 1

The reference y _d with desired trial length T _d = 50

Fig. 2

Norm of tracking error in each iteration of ILC with nonuniform trial length: N₁ = N₂ = 5

Moreover, Fig. 3 gives the tracking error profiles for 10th, 20th, 80th, 100th iterations, respectively.

Fig. 3

Tracking error profiles of ILC with non-uniform trial length: N₁ = N₂ = 5

To demonstrate the effect of N₁ and N₂ on the convergence speed of the tracking error, we fix the learning gain L = 0.5I_50×50 and set N₁ = N₂ = 30. Here, ${T_i} \in \{20,21, \cdots ,80\} ,P[{T_i} = {\tau _m}] = {1 \over {61}}$ and m ∈ {0, 1,⋯, 60}. It can be seen from Fig. 4 that the convergence will be achieved after more than 60 iterations, i.e., the convergence speed is obviously slower than the case N₁ = N₂ =5.

Fig. 4

Norm of tracking error in each iteration of ILC with nonuniform trial length: N₁ = N₂ =30

To show the effectiveness of the proposed ILC scheme with randomly varying initial states, we fix the learning gain L = 0.5I_50×50 and N₁ = N₂ = 5. Assume x _i (0) is a stochastic variable with probability $P[{x_i}(0) = {v_1}] = {1 \over 3},P[{x_i}(0) = {v_2}] = {1 \over 3}$ and $P[{x_i}(0) = {v_3}] = {1 \over 3}$, where v₁ = [0, 0, −1]^T, v₂ = [0, 0, 0]^T and v₃ = [0, 0, 1]^T. Fig. 5 shows that the mathematical expectation of the tracking error E(e _i ) will converge to zero within 80 iterations. The tracking error profiles of the proposed ILC scheme and the ILC scheme without average operator in [19] are illustrated in Figs. 6 and 7, respectively. It is obvious that the performance of the proposed ILC scheme is superior to that of the ILC scheme in [19] under the situation of randomly varying initial states. Similarly, in [20, 21], the identical initialization condition is also indispensable.

• Example 2. Time-varying system.

Fig. 5

The mathematical expectation of tracking errors when the proposed ILC scheme is applied to (36)

Fig. 6

Tracking error profiles when the proposed ILC scheme is applied to (36)

Fig. 7

Tracking error profiles when the ILC scheme in [19] is applied to (36)

In order to show the effectiveness of our proposed ILC algorithm for time-varying systems, we consider the discrete-time linear time-varying system as

$$\begin{array}{*{20}c} {x_i (k + 1) = \left( {\begin{array}{*{20}c} {0.2e^{ - \tfrac{k} {{100}}} } & { - 0.6} & 0 \\ 0 & {0.5} & {\sin (k)} \\ 0 & 0 & {0.7} \\ \end{array} } \right)} \\ {y_i (k) = \left( {\begin{array}{*{20}c} { - 0.5} & {1.5} & 0 \\ \end{array} } \right)x_i (k)} \\ \end{array} x_i (k) + \left( {\begin{array}{*{20}c} {1.3} \\ {0.5} \\ {0.6} \\ \end{array} } \right)u_i (k)$$

(37)

where ${x_i}(0) = {[0,0,0]^{\rm{T}}},i \in {\cal N}$. Similarly as Example 1, let the desired trajectory be ${y_d}(k) = \sin ({{2\pi k} \over {50}}) + \sin ({{2\pi k} \over 5}) + \sin (50\pi k),k \in {{\cal I}_d} = \{1,2, \cdots ,50\}$ in the first iteration. Assume that T _i satisfies the Gaussian distribution with mean 50 and standard deviation 10, i.e., T _i ∼ N (50, 100). Since T _i is integer in this example, it is generated approximately by the Matlab command “round(50 +10* randn(1, 1))”. Further, set the learning gain as L = 2I_50×50. The performance of the tracking error ∥e _i ∥ is presented in Fig. 8, where ∥e _i ∥ will converge within 50 iterations. In addition, Fig. 9 gives tracking error profiles at 10th, 20th, 80th and 100th iterations.

Fig. 8

Norm of tracking error in each iteration of ILC with T _i ∼ N (50, 100)

Fig. 9

Tracking error profiles of ILC with T _i ∼ N(50, 100)

6 Conclusions

This paper presents the ILC design and analysis results for systems with non-uniform trial lengths under the framework of lifted systems. Due to the variation of the trial lengths, a modified ILC scheme is developed by applying an iteration-average operator. The learning condition of ILC that guarantees the convergence of tracking error in the sense of mathematical expectation is derived. The proposed ILC scheme mitigates the requirement on classic ILC that each trial must end in a fixed duration. In addition, the identical initialization condition might be removed. Therefore, the proposed ILC scheme is applicable to more repetitive control processes. The formulation of ILC with nonuniform trial lengths is novel and could be extended to other control problems that are perturbed by random factors, for instance, control systems with random factors in communication channels.