Introduction

In recent years, most modern vehicles have been equipped with driver assistance systems for improved driver and passenger security, for example the anti-lock braking systems (ABS) for better braking performance and electronic stability programs (ESP) to stabilize yaw motion. Safety and driver assistance systems greatly reduce potential injury risk during vehicle accidents. Today, airbags are integrated in most of the vehicles. This has resulted in a decreased number of serious injuries during vehicle crashes. In past few years, new systems such as side and roof airbags have been introduced which cover even more accidental situations rather than merely frontal crashes. However, vehicle rollover still poses serious threat to occupant safety. While rollover occurs only in 3% of all passenger car accidents, they contribute to 33% of the number of fatal accidents in the US[1]. These figures highlight the potential danger to the passengers during rollover. The reduction of vehicle rollover occurrence is an important part in providing increased passenger safety.

Rollover can occur during typical driving situations, this is covered above for vehicles as well as passengers. Examples include excessive speed while negotiating sharp turns, sudden avoidance of obstacles and sharp lane change maneuvers. In such cases, rollover occurs as a direct result of the lateral wheel forces which are induced during these maneuvers[2, 3]. In earlier studies on the detection of vehicle rollover, the concept of a static rollover threshold was used, but this is only useful at steady state. In [4–7], time-to-rollover (TTR) is proposed to estimate the time until rollover occurs and a direct yaw moment control using differential braking is performed. Hac et al. described a rollover index using a model-based roll estimator in [8]. In [9], a rollover index (RI) combining the lateral dynamics model-based estimator and vertical dynamics model-based estimator is proposed. Traditionally, some estimation of the vehicle load transfer ratio (LTR) has been used as a basis for the design of rollover prevention systems[10].The LTR quantity can be simply defined as the difference between the normal forces on the right and left hand sides of the vehicle divided by their sum. Clearly, LTR varies within [−1, 1], and for a perfectly symmetric and straightly driven car, it is zero.

In this work, we use the dynamic load transfer ratio LTR d as rollover index which is computed using the estimated roll angle and roll rate. In order to anticipate the detection, the LTR d rate is used to compute the time to rollover (TTR). A model-based roll state estimator is designed in presence of the road bank angle using the H∞ approach and taking into account the unmeasurable premise variables[11, 12]. The nonlinear model, as derived from three-degree-of-freedom vehicle lateral dynamics, is represented by a Takagi-Sugeno (T-S) fuzzy model[13] which is very efficient to represent the lateral force nonlinearities[12, 14, 15]. This representation has been widely used and studied in the past years (see for example [15–22]).

The structure of the paper is as follows. Section 2 introduces the used model represented by a T-S fuzzy model, the parameter identification of the model and its validation using the CarSim software. Section 3 presents a rollover detection study, the LTR d and the TTR are discussed in presence of road bank angle. A T-S model-based roll state estimator using the H∞ approach is designed in Section 4. Section 5 contains simulation results and shows the rollover index computed in two tests conducted using the CarSim software.

Vehicle modeling and parameters identification

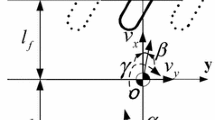
The model used in this work describes vehicle lateral and roll dynamics, which is obtained by considering the well known single-track (bicycle) model with a roll degree of freedom (Fig. 1). The three-dimensional model with road bank angle and nonlinear tire characteristics of the four wheeled vehicle behavior can be described by the following differential equations[23–25]:

$$\left\{{\matrix{{m(v\dot \beta + v\dot \psi - {{\ddot \phi}_v}h) = 2{F_{yf}} + 2{F_{yr}} - mg{\phi _r}} \hfill \cr {{I_z}\ddot \psi = 2{F_{yf}}{l_f} - 2{F_{yr}}{l_r}} \hfill \cr {{I_x}{{\ddot \phi}_v} = {m_s}gh({\phi _v} + {\phi _r}) + {m_s}{a_y}h - {K_\phi}{\phi _v} - {C_\phi}{{\dot \phi}_v}} \hfill \cr}} \right.$$
(1)

with β denoting the sideslip angle, ψ, ϕ v and ϕ r the vehicle yaw, the roll angle and the road bank angle, respectively; F f the cornering force of the two front tires and F r the cornering force of the two rear tires. For further description of the parameters appearing in the vehicle dynamics model, refer to Table 1.

Fig. 1
figure 1

Vehicle parameters description

Full size image
Table 1 Vehicle parameter definitions
Full size table

The Pacejka tire model[26] gives the cornering forces F yf and F yr as a function of tire slip angles by the following nonlinear expressions:

$$\left\{{\matrix{{{F_{yf}} = {D_f}\sin [{C_f}{{\tan}^{- 1}}{B_f}(1 - {E_f}){\alpha _f} + {E_f}{{\tan}^{- 1}}({B_f}{\alpha _f})]} \hfill \cr {{F_{yr}} = {D_r}\sin [{C_r}{{\tan}^{- 1}}{B_r}(1 - {E_r}){\alpha _r} + {E_r}{{\tan}^{- 1}}({B_r}{\alpha _r})]} \hfill \cr}} \right.$$
(2)

with

$$\matrix{{{\alpha _f} = {\delta _f} - {{{l_f}\dot \psi} \over v} - \beta} \hfill \cr {{\alpha _r} = {{{l_r}\dot \psi} \over v} - \beta} \hfill \cr}$$
(3)

with δ as the front steering angle, α f as the slip angle of the front tires and α r is the slip angle of the rear tires (Fig. 1). Coefficients B i , C i , D i and Ei (i = f, r) depend on the tire characteristics, road adhesion coefficient and the vehicle operational conditions. The above Pacejka model describes such phenomena, but is hardly usable since it depends on many nonlinearities and varying parameters that need to be known.

Lateral forces are assumed in other studies to be proportional to the slip angle, i.e.,

$$\left\{{\matrix{{{F_{yf}} = {C_f}{\alpha _f}} \hfill \cr {{F_{yr}} = {C_r}{\alpha _r}.} \hfill \cr}} \right.$$
(4)

It is obvious that when the slip angles are very small, the obtained linear model works very well (Fig. 2). However, in case of it is a bit ambiguous slip angles, the nonlinear model must be considered[27].

Fig. 2
figure 2

Comparison of the tire models

Full size image

T-S fuzzy representation of the vehicle model

In this work, we take into account the nonlinearities of the cornering forces by considering a T-S fuzzy representation of the tire model described by the following rules:

$$\begin{array}{*{20}c} {If \left| {\alpha _f } \right| is M_1 ,} & {then\left\{ {\begin{array}{*{20}c} {F_{yf} = C_{f1} \alpha _f } \\ {F_{yr} = C_{r1} \alpha _r } \\ \end{array} } \right.} \\ {If \left| {\alpha _f } \right| is M_2 ,} & {then\left\{ {\begin{array}{*{20}c} {F_{yf} = C_{f2} \alpha _f } \\ {F_{yr} = C_{r2} \alpha _r } \\ \end{array} } \right.} \\ \end{array} $$
(5)

where C fi , C ri are the front and rear tire cornering stiffness which depend on the road friction coefficient and the vehicle parameters. M1(M2) is a fuzzy set for small (large) slip angles.

  • Remark 1. Since α f and α r have similar values (the same fuzzy sets), the proposed rules are made only for α f . This assumption allows reducing the number of membership functions and parameters to identify.

The overall forces are obtained by

$$\left\{{\matrix{{{F_{yf}} = {\mu _1}(\vert {\alpha _f}\vert){C_{f1}}{\alpha _f} + {\mu _2}(\vert {\alpha _f}\vert){C_{f2}}{\alpha _f}} \hfill \cr {{F_{yr}} = {\mu _1}(\vert {\alpha _f}\vert){C_{r1}}{\alpha _r} + {\mu _2}(\vert {\alpha _f}\vert){C_{r2}}{\alpha _r}} \hfill \cr}} \right.$$
(6)

with H j (j = 1, 2) is the j-th bell curve membership function of fuzzy set M j . They satisfy the following properties:

$$\left\{{\matrix{{\sum\limits_{i = 1}^2 {{\mu _i}} (\vert {\alpha _f}\vert) = 1} \hfill \cr {0 \leq {\mu _i}(\vert {\alpha _f}\vert) \leq 1,\quad i = 1,2.} \hfill \cr}} \right.$$
(7)

The expressions of the membership functions used are

$${\mu _i}(\vert {\alpha _f}\vert) = {{{\omega _i}(\vert {\alpha _f}\vert)} \over {\sum\limits_{i = 1}^2 {{\omega _i}(\vert {\alpha _f}\vert)}}},\quad i = 1,2$$
(8)

with

$${\omega _i}(\vert {\alpha _f}\vert) = {1 \over {{{\left({1 + \left\vert {\left({{{\vert {\alpha _f}\vert - {c_i}} \over {{a_i}}}} \right)} \right\vert} \right)}^{2{b_i}}}}}.$$
(9)

Using the above approximations of nonlinear lateral forces and introducing equations (6) in the nonlinear model (1), the following T-S fuzzy model is obtained:

$$\matrix{{\dot x(t) = \sum\limits_{i = 1}^2 {{\mu _i}(\vert {\alpha _f}\vert)} \left({{A_i}x(t) + {B_i}{\delta _f}(t)} \right) + {B_w}{\phi _r}()} \hfill \cr {y(t) = Cx(t)} \hfill \cr}$$
(10)

with

$$\begin{array}{*{20}c} {A_1 = \left[ {\begin{array}{*{20}c} { - \tfrac{{\sigma _i I_{x_{eq} } }} {{mI_x v}}} & {\tfrac{{\rho _i I_{x_{eq} } }} {{mI_x v^2 }} - 1} & { - \tfrac{{hC_\varphi }} {{I_x v}}} & {\tfrac{{h(m_s gh - k\varphi )}} {{I_x v}}} \\ {\tfrac{{\rho _i }} {{I_2 }}} & { - \tfrac{{\tau _i }} {{I_z v}}} & 0 & 0 \\ { - \tfrac{{m_s h\sigma _i }} {{mI_x }}} & {\tfrac{{m_s h\rho _i }} {{mI_x v}}} & { - \tfrac{{C_\varphi }} {{I_x }}} & {\tfrac{{(m_s gh - k_\varphi )}} {{I_x }}} \\ 0 & 0 & 1 & 0 \\ \end{array} } \right]} \\ {\begin{array}{*{20}c} {B_i = \left[ {\begin{array}{*{20}c} {2\tfrac{{C_{fi} I_{x_{eq} } }} {{mI_x v}}} \\ {2\tfrac{{C_{fi} l_f }} {{I_z }}} \\ {2\tfrac{{m_s hC_{fi} }} {{mI_x }}} \\ 0 \\ \end{array} } \right],} & {B_w = \left[ {\begin{array}{*{20}c} { - \tfrac{g} {v}} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right],} \\ \end{array} } \\ {C = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ \end{array} } \right]} \\ \end{array} $$

where \(x(t) = {\left[ {\beta (t)\quad \dot \psi (t)\quad {{\dot \phi}_v}(t)\quad {\phi _v}(t)} \right]^{\rm{T}}}\) is the state vector of the model, I xeq denotes the equivalent roll moment of inertia of the vehicle about the roll axis, which is given by

$${I_{{x_{eq}}}} = {I_x} + {m_s}{h^2}$$
(11)

and σ i , ρ i , τ i are auxiliary variables introduced in order to simplify the model description; they are defined as

$$\matrix{{\quad {\sigma _i} = 2({C_{ri}} + {C_{fi}})} \hfill \cr {{\rho _i} = 2({l_r}{C_{ri}} - {l_f}{C_{fi}})} \hfill \cr {{\tau _i} = 2(l_f^2{C_{fi}} + l_r^2{C_{ri}}).} \hfill \cr}$$
(12)

Parameter identification of the vehicle model

Using an identification method based on the Levenbenrg-Marquadt algorithm[15] combined with the least square method, parameters of the membership functions (a i , b i , and c i ) and stiffness coefficient C fi and C ri are obtained so that the T-S model (6) approximates the cornering forces for given vehicle parameters and road conditions. For the vehicle parameters defined in Table 2 and for a dry road, the obtained values are given in Table 3.

Table 2 Simulation vehicle parameters
Full size table
Table 3 Parameters of the membership functions
Full size table

The quality of the parameter identification results is examined in comparison with the simulation results obtained from the professional vehicle dynamics software CarSim[28]. One of the comparison results is shown in Fig. 3, where simulation is carried out under a fishhook manoeuver (Fig. 4) at a speed of 50 km/h. The simulation results show that the identified T-S model shows a good representation of the actual states measured using CarSim.

Fig. 3
figure 3

Comparison with CarSim simulator at 50 km/h

Full size image
Fig. 4
figure 4

Steering wheel angle used in the fishhook test

Full size image

Rollover detection study

Lateral load transfer

Lateral load transfer is the change in the normal force acting on the tires due to both the acceleration of the centre of gravity (CG), and shifting of the position of the CG in the y direction due to movement of suspension. Fig. 5 illustrates lateral load transfer in the vertical plane.

Fig. 5
figure 5

Vehicle roll model

Full size image

The load transfer ratio and LTR d in presence of the road bank angle

The load transfer ratio (LTR) can be defined as the difference between the normal forces on the right tires and the left tires of the vehicle divided by their sum. Assuming no vertical motion exists, the LTR is given by

$${\rm{LTR}} = {{{F_{zl}} - {F_{zr}}} \over {{F_{zl}} + {F_{zr}}}} = {{{F_{zl}} - {F_{zr}}} \over {mg}}$$
(13)

where F zl and F zr are the vertical left and right tire forces, respectively. It is apparent that LTR varies within [−1, 1], and for a perfectly symmetric car which is driving straight, it is zero. The extrema are reached in case of wheel lift-off on any one side of the vehicle. In that case LTR becomes 1 or −1, depending on the side lifted off.

The estimation of the LTR is very difficult since normal force sensors are expensive. An expression for LTR which depends on the roll states and vehicle parameters can be obtained. This is denoted by LTR d . In order to derive LTR d we resolve weight (m s g) and pseudo-force (m s a y ) into components in the vehicle-fixed y and z directions; the following dynamics are obtained:

$${m_s}{a_y} + {m_s}gh({\phi _v} + {\phi _r}) - {C_\phi}{\dot \phi _v} + {K_\phi}{\phi _v} = 0.$$
(14)

We can also derive a torque balance equation for the sprung and unsprung masses about the left tire roll axis as

$${F_{zr}}T + {m_s}{a_y}h + {m_s}gh{\phi _r} - {m_s}g({T \over 2} - h{\phi _v}) - {m_u}g{T \over 2} = 0.$$
(15)

By substituting (14) and (15) into (13), we obtain the following expression for LTR d :

$${\rm{LT}}{{\rm{R}}_{\rm{d}}} = {2 \over {mgT}}({C_\phi}{\dot \phi _v} + {K_\phi}{\phi _v}).$$
(16)

  • Remark 2. In the above section, it is shown that the presence of the road bank angle affects the LTR d through the roll angle and roll rate.

Time to rollover computation

Even though the LTR d can be used as a rollover index to accurately detect the tire lift off, it can be pointed out that the LTR d is not able to anticipate or detect an impending rollover. The time to rollover (TTR) is one of the most efficient indicators in order to anticipate the rollover detection. It is defined as the time remaining before wheel lift off will occur, which gives a clear indication of the beginning of rollover. A TTR computation is proposed in [5, 6] by assuming that the input steering angle stays fixed at its current position in the foreseeable future; it is defined as the time taking by the vehicle sprung mass to reach its critical roll angle. In order to take account of the steering angle rate, two advanced versions of the TTR are developed, based on the fifth-order linear vehicle dynamic model in [29].

In this study, the TTR is computed as follows: Assuming that the LTR d increases or decreases at its current rate in the near future, the time taken by the load transfer ratio to reach 1 or −1 is computed using the following equations:

$${\rm{TTR}} = {{1 - {\rm{LT}}{{\rm{R}}_d}} \over {{R_{{\rm{LTR}}}}}},\quad {\rm{if}}\quad {\rm{LTR}} > 0$$
(17)
$${\rm{TTR}} = {{- 1 - {\rm{LT}}{{\rm{R}}_d}} \over {{R_{{\rm{LTR}}}},}}\quad {\rm{if}}\quad {\rm{LTR}} < 0$$
(18)

with RLTR is the LTR d rate, which is obtained from a filtered differential signal of the LTR d .

Under normal driving conditions, there is no risk of rollover and the LTR d is close to zero. In this case the TTR is usually very large and increases excessively. For example, if the vehicle is driven straight, there is no roll motion at all. Therefore, the TTR approaches infinity. For implementation considerations, TTR is saturated in 10 s when the LTR d is too small.

Model-based roll state estimator with road bank angle consideration

As shown in the above section, in order to compute the LTR d it is necessary to know the roll angle and roll rate which are difficult and very expensive to measure directly. Roll angle and roll rate can be estimated from measurable signals such as the yaw rate and the vehicle parameters. In this study, both the roll angle and the roll rate are estimated in presence of the road bank angle as bounded unknown input disturbances in the used T-S vehicle model. Vehicle dynamic variables such as the yaw rate, steering angle and vehicle velocity are also measured (Fig. 6).

Fig. 6
figure 6

Vehicle state estimator

Full size image

T-S estimator design conditions

Using (10), a T-S model based estimator for the estimation of the roll angle and the roll rate in the presence of the unknown road bank angle is represented as

$$\matrix{{\dot \hat x(t) = \sum\limits_{i = 1}^2 {{\mu _i}} (\vert {{\hat \alpha}_f}\vert)({A_i}\hat x(t) + {B_i}\delta (t) + {L_i}(y(t) - \hat y(t)))} \hfill \cr {\quad \quad \quad \quad \quad \quad \quad \hat y(t) = C\hat x(t).} \hfill \cr}$$
(19)

By using measurable signals such as the tire steering angle and yaw rate and considering unmeasurable premise variables, the roll angle and the roll rate can be estimated with (19). The aim of the design is to determine gain matrices L i , which guarantee the asymptotic convergence of \(\hat x(t)\) towards x(t). Let us define the state estimation error as

$$e(t) = x(t) - \hat x(t).$$
(20)

The dynamics of the state estimation error is governed by

$$\matrix{{\dot e(t) = \sum\limits_{i = 1}^2 {} \sum\limits_{j = 1}^2 {{\mu _i}} (\vert {{\hat \alpha}_f}\vert){\mu _j}(\vert {\alpha _f}\vert)(({A_i} - {L_i}C)e(t) +} \hfill \cr {\quad \quad \;\;\Delta {A_{ij}}x(t) + \Delta {B_{ij}}\delta (t)) + {B_w}{\phi _r}(t)} \hfill \cr}$$
(21)

with

$$\Delta {A_{ij}} = {A_j} - {A_i},\quad \Delta {B_{ij}} = {B_j} - {B_i}.$$
(22)

Let us define

$${x_e}(t)\left[ {\matrix{{e(t)} \cr {x(t)} \cr}} \right],\quad w = \left[ {\matrix{{\delta (t)} \cr {{\phi _r}(t)} \cr}} \right].$$
(23)

The augmented system formed from system (10) and state estimation error (21) can now be expressed as

$${\dot x_e}(t) = \sum\limits_{i = 1}^2 {} \sum\limits_{j = 1}^2 {} {\mu _i}(\vert {\hat \alpha _f}\vert){\mu _j}(\vert {\alpha _f}\vert)({\bar A_{ij}}{x_e}(t) + {\bar B_{ij}}w(t))$$
(24)

with

$$\begin{array}{*{20}c} {\bar A_{ij} = \left[ {\begin{array}{*{20}c} {A_i - L_i C} & {\Delta A_{ij} } \\ 0 & {A_j } \\ \end{array} } \right],} & {\bar B_{ij} = \left[ {\begin{array}{*{20}c} {\Delta B_{ij} } & {B_w } \\ {B_j } & {B_w } \\ \end{array} } \right].} \\ \end{array} $$
(25)

  • Remark 3. Since w(t) constitutes of the steering angle and the road bank angle, it can be logically assumed to have a finite energy.

The T-S estimator gains have been computed by considering the effect of the road bank angle on the state estimation errors. One possible method is to minimize the ℒ2 gain (H∞ norm) from disturbances to the estimation errors.

The ℒ2 gain between vector w(t) and estimation error e(t) is defined by the following quantity:

$$\gamma = \sup {{\left\Vert {e(t)} \right\Vert} \over {\left\Vert {w(t)} \right\Vert}}.$$
(26)

By the definition of the supremum and the ℒ2 gain, (26) can be expressed as

$$\int_0^\infty {e{{(t)}^{\rm{T}}}} e(t)\;{\rm{d}}t \leq {\gamma ^2}\int_0^{^\infty} {w{{(t)}^{\rm{T}}}} w(t)\;{\rm{d}}t.$$
(27)

  • Theorem 1. If there exists positive and symmetric matrices P1 and P2, matrices M j and positive scalar γ satisfying the following LMI for i, j = 1, 2:

    $$\left[ {\begin{array}{*{20}c} {\Theta _i } & {P_1 \Delta A_{ij} } & {P_1 \Delta B_{ij} } & {P_1 B_w } \\ {\Delta A_{ij}^T P_1 } & {\Psi _j } & {P_2 B_j } & {P_2 B_w } \\ {\Delta B_{ij}^T P_1 } & {B_j^T P_2 } & { - \gamma ^2 I} & 0 \\ {B_w^T P_1 } & {B_w^T P_2 } & 0 & { - \gamma ^2 I} \\ \end{array} } \right] < 0$$
    (28)

    with

    $${\Theta _i} = A_i^{\rm{T}}{P_1} + {P_1}{A_i} - {M_i}C - {C^{\rm{T}}}M_i^{\rm{T}} + I$$
    (29)
    $${\Psi _j} = A_j^{\rm{T}}{P_2} + {P_2}{A_j}$$
    (30)

    then estimation error (20) converges asymptotically toward zero and satisfies the H∞ performance (27). The observer gains are given by \({L_i} = P_1^{- 1}{M_i}\).

  • Proof. Let us consider the following Lyapunov function candidate:

    $$V({x_e}) = {x_e}{(t)^{\rm{T}}}P{x_e}(t)$$
    (31)

    with P = PT > 0. The state estimation error can be written as

    $$e(t) = {C_e}{x_e}(t)$$
    (32)

    with

    $${C_e} = \left[ {I\quad 0} \right].$$
    (33)

    System (24) is stable and the H ∞ norm of the transfer function between unknown input w(t) and the state estimation errors e(t) is bounded by γ > 0 if the following condition holds:

    $${J_\infty} = \dot V({x_e}) + e{(t)^{\rm{T}}}e(t) - {\gamma ^2}w{(t)^{\rm{T}}}w(t) < 0.$$
    (34)

    Substituting (24) into (34) gives

    $$\matrix{{\sum\limits_{i = 1}^2 {} \sum\limits_{j = 1}^2 {{\mu _i}} ({{\hat \alpha}_f}){\mu _j}({\alpha _f})({x_e}{{(t)}^{\rm{T}}}\bar A_{ij}^{\rm{T}}P{x_e}(t) +} \hfill \cr {\quad {x_e}{{(t)}^{\rm{T}}}P{{\bar A}_{ij}}{x_e}(t) + w{{(t)}^{\rm{T}}}\bar B_{ij}^{\rm{T}}P{x_e}(t) +} \hfill \cr {\quad {x_e}{{(t)}^{\rm{T}}}P{{\bar B}_{ij}}w(t)) + {x_e}{{(t)}^{\rm{T}}}{x_e}(t) -} \hfill \cr {\quad {\gamma ^2}w{{(t)}^{\rm{T}}}w(t) < 0.} \hfill \cr}$$
    (35)

Inequality (35) can be expressed as an equivalent inequality as

$$\sum\limits_{i = 1}^2 {\sum\limits_{j = 1}^2 {\mu _i \left( {\left| {\hat \alpha _f } \right|} \right)\mu _j \left( {\left| {\alpha _f } \right|} \right)\left[ {x_e } \right]T\left[ {\begin{array}{*{20}c} {X_{ij} } & {P\bar B_{ij} } \\ {\bar B_{ij}^T P} & { - \gamma ^2 I} \\ \end{array} } \right]\left[ {x_e } \right] < 0} } $$
(36)

with

$${X_{ij}} = \bar A_{ij}^{\rm{T}}P + P{\bar A_{ij}} + C_e^{\rm{T}}{C_e}.$$
(37)

According to the convex sum property of the activation functions, inequality (36) holds if the following conditions are satisfied:

$$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} { - \bar A_{ij}^T P + P\bar A_{ij} + C_e^T C_e } & {P\bar B_{ij} } \\ {\bar B_{ij}^T P} & { - \gamma ^2 I} \\ \end{array} } \right] < 0,} & {\forall i,j = 1,2.} \\ \end{array} $$
(38)

These constraints are nonlinear. In order to get LMI conditions, let us consider the following particular form of matrix P:

$$P = \left[ {\begin{array}{*{20}c} {P_1 } & 0 \\ 0 & {P_2 } \\ \end{array} } \right].$$
(39)

By substituting (25) and (39), inequality (39) can be written as

$$\left[ {\begin{array}{*{20}c} {\Omega _i } & {P_1 \Delta A_{ij} } & {P_1 \Delta B_{ij} } & {P_1 B_w } \\ {\Delta A_{ij}^T P_1 } & {\Psi _j } & {P_2 B_j } & {P_2 B_w } \\ {\Delta B_{ij}^T P_1 } & {B_j^T P_2 } & { - \gamma ^2 I} & 0 \\ {B_w^T P_1 } & {B_w^T P_2 } & 0 & { - \gamma ^2 I} \\ \end{array} } \right] < 0$$
(40)

with

$${\Omega _i} = {({A_i} - {L_i}C)^{\rm{T}}}{P_1} + {P_1}({A_i} - {L_i}C) + I$$
(41)
$${\Psi _j} = A_j^{\rm{T}}{P_2} + {P_2}{A_j}.$$
(42)

Using change of variable as M i = P1 L i , condition (40) is linear in variables P1, P2 and M i , which leads to the equivalent condition given by (28). Indeed, it suffices to satisfy (28) to guarantee \(\dot V(t) < 0\) with the γ-attenuation (27). □

To obtain less conservative LMI conditions of Theorem 1, we use the technique developed in [21], and the following results are obtained.

  • Corollary 1. If there exists matrices P1 > 0 and P2 > 0, matrices Q ij , M j and scalar γ, the following LMIs hold:

    $${\Gamma _{ii}} + {Q_{ii}} < 0,\quad \quad i = 1,2$$
    (43)
    $${\Gamma _{ij}} + {\Gamma _{ji}} + {Q_{ij}} + {Q_{ji}} < 0,\quad \quad i < j$$
    (44)
    $$\left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } \\ {Q_{12}^T } & {Q_{22} } \\ \end{array} } \right] > 0$$
    (45)

    with

    $$\Gamma _{ij} = \left[ {\begin{array}{*{20}c} {\Theta _j } & {P_1 \Delta A_{ij} } & {P_1 \Delta B_{ij} } & {P_1 B_w } \\ {\Delta A_{ij}^T P_1 } & {\Psi _i } & {P_2 B_i } & {P_1 B_w } \\ {\Delta B_{ij}^T P_1 } & {B_i^T P_2 } & { - \gamma ^2 I} & 0 \\ {B_w^T P_1 } & {B_w^T P_2 } & 0 & { - \gamma ^2 I} \\ \end{array} } \right] < 0$$
    (46)

    then estimation error (20) is stable and satisfies the H ∞ performance (27). The observer gains are given by \(P_1^{- 1}{M_i}\).

Simulation results

The developed model based estimator has been implemented in a professional simulator in order to be tested under different driving tests. Two fishhook tests are conducted with different steering wheel angles (Fig. 7). The input steering angle used in test 2 is defined such that the wheel lift off occurs at 2.8 s, whereas in test 1 no wheel lift off occurs. In this simulation, the vehicle is driven at a constant speed of 110 km/h in a 6% banked road.

Fig. 7
figure 7

The used steering angles in tests 1 and 2

Full size image

Using the model parameters given in Table 2, the resolution of LMI constraints (28), the LMI toolbox of Matlab leads to the following P i and M i matrices:

$$\begin{array}{*{20}c} {P_1 = 10^4 \left[ {\begin{array}{*{20}c} {0.0003} & {0.0145} & {0.0022} & {0.0087} \\ {0.0145} & {1.6132} & {0.2351} & {0.4366} \\ {0.0022} & {0.2351} & {0.0343} & {0.0632} \\ {0.0087} & {0.4366} & {0.0632} & {1.1349} \\ \end{array} } \right]} \\ {P_2 = 10^3 \left[ {\begin{array}{*{20}c} {0.4271} & {0.0101} & { - 0.001} & {0.0788} \\ {0.0101} & {0.0961} & {0.0033} & {0.0410} \\ { - 0.001} & {0.0033} & {0.0025} & {0.0059} \\ {0.0788} & {0.0410} & {0.0059} & {0.1457} \\ \end{array} } \right]} \\ {M_1 = 10^4 \left[ {\begin{array}{*{20}c} { - 0.099} & { - 5.277} & { - 0.782} & { - 8.482} \\ \end{array} } \right]^T } \\ {M_2 = 10^5 \left[ {\begin{array}{*{20}c} {0.007} & {1.096} & {0.160} & { - 0.417} \\ \end{array} } \right]^T .} \\ \end{array} $$

Then, the following observer gains are obtained:

$$\begin{array}{*{20}c} {L_1 = \left[ {\begin{array}{*{20}c} {222.130} & {131.155} & { - 920.682} & { - 8.385} \\ \end{array} } \right]^T } \\ {L_2 = \left[ {\begin{array}{*{20}c} {192.989} & {75.474} & { - 468.130} & { - 8.131} \\ \end{array} } \right]^T .} \\ \end{array} $$

The vehicle states estimated by the designed observer are compared to the actual states measured in CarSim for the conducted tests (Figs. 8 and 9). In both tests the designed estimator shows good performance. However, between 3 s and 3.6 s (the moment of the wheel lift off), the estimation is not quite that good. This is due to the vehicle model which does not take into account the vehicle behavior after the rollover. Fig. 10 shows the simulation results of the LTR d computation for the two tests. The TTR shows good efficiency for the rollover detection, but the proposed rollover indicator, which is the TTR, shows better anticipation in the rollover detection (Fig. 10). This advantage is very interesting since the rollover has to be avoided in a matter of seconds.

Fig. 8
figure 8

Simulation results of the vehicle state estimator in test 1

Full size image
Fig. 9
figure 9

Simulation results of the vehicle state estimator in test 2

Full size image
Fig. 10
figure 10

Comparison of the LTR d and TTR computed in tests 1 and 2

Full size image

Conclusion and future works

A model-based roll state estimator is designed in presence of the road bank angle using the H ∞ approach. The nonlinear model given by three-degrees-of freedom vehicle lateral dynamics is represented by a T-S fuzzy model. This representation takes into account the nonlinearities introduced by the lateral forces. The designed fuzzy observer shows good performance even in presence of unknown road bank angle. Design conditions are formulated in LMI terms that are easy to solve using numerical tools. A dynamic approximation of the lateral transfer ratio is used to compute the time to rollover (TTR) which shows good efficiency and good anticipation in detecting of impending rollover. The proposed fuzzy observer and the rollover index are tested through the CarSim software in two different tests. In further works, we will extend the results by considering more complex vehicle models in order to take account of the vehicle behavior after the wheel lift off. An experimental study will also be developed in the near future.