Forecasting accuracy of machine learning and linear regression: evidence from the secondary CAT bond market

Abstract

The main challenge in empirical asset pricing is forecasting the future value of assets traded in financial markets with a high level of accuracy. Because machine learning methods can model relationships between explanatory and dependent variables based on complex, non-linear, and/or non-parametric structures, it is not surprising that machine learning approaches have shown promising forecasting results and significantly outperform traditional regression methods. Corresponding results were achieved for CAT bond premia forecasts in the primary market. However, since secondary market data sets have a panel data structure, it is unclear whether the results of primary market studies can be applied to the secondary market. Against this background, this study aims to build the first out-of-sample forecasting model for CAT bond premia in the secondary market, comparing different modeling approaches. We apply random forest and neural networks as representatives of machine learning methods and linear regression based on a comprehensive data set of CAT bond issues and across various forecasting settings and show that random forest forecasts are significantly more precise. Because the lack of transparency of machine learning methods may limit their applicability, especially for institutional investors, we show ways to identify important variables in the context of random forest price forecasting.

1 Introduction

In the context of asset price forecasting, machine learning approaches have recently shown promising results, significantly outperforming the forecasting capabilities of traditional regression methods (Bianchi et al. 2021; Gu et al. 2020). While most studies focus on the stock market, there are only few papers that analyze bonds. Bianchi et al. (2021) compared different forecasting models to predict future bond excess returns. They showed that neural networks outperform penalized regression models as well as different regression tree models. Götze et al. (2020) and Makariou et al. (2021) forecast catastrophe (CAT) bond primary market premia and both show that random forests outperform linear regression models. In addition, Götze et al. (2020) established a neural network model, which was also outperformed by the random forest model in terms of forecasting accuracy. Compared to the primary market, a greater amount of information and possible explanatory determinants are available in the secondary market, such as the historical change in premia represented by momentum variables. In such an environment, it is unclear whether the results of the primary market studies are transferable to the secondary market. Against this background, the first objective of this study is to analyze price forecasting accuracies of traditional linear regression and selected machine learning methods in the CAT bond secondary market. In addition, this study contributes to the existing literature by providing the first out-of-sample prediction model for the CAT bond secondary market.

Although machine learning methods are possibly superior to linear regression in modeling complex relationships, a major advantage of traditional linear regression over advanced machine learning methods lies in its transparency regarding the functional relationships between the (dependent) price variable and independent variables. Especially in the context of institutional investors or issuers, the transparency of the applied methods is of particular importance because of the regulatory requirements.¹ Machine learning methods are often referred to as black boxes, which would contradict this requirement. In addition, especially in the field of machine learning, program codes (e.g., in R), which are made available on the internet by the programming community, are used. To check the implemented methods for plausibility, it must be clarified whether the variable selection made by the model appears plausible. Specifically, it is necessary to clarify which independent variables are of particular importance in forecasting the price variable, so that it is clear on which variables the forecast is based. Consequently, the second objective of this study is to determine the possibility of identifying relevant price influencing variables when applying machine learning methods.

In the present study, we consider the CAT bond secondary market, analyze the forecasting performance of random forests and artificial neural networks as relevant representatives of machine learning methods, and compare them with the performance of traditional linear regression. CAT bonds can be regarded as capital market-based reinsurance against natural disasters and represent an alternative to traditional reinsurance. The CAT bond market has increased continuously since its inception in the 1990s. Therefore, CAT bond pricing has become an important topic in the literature on insurance and asset pricing. The literature consists of a wide range of models that examine the relationships between CAT bond premia and relevant influencing factors based on traditional regression methods in the primary market (Lane 2000; Wang 2000, 2004; Galeotti et al. 2013; Braun 2016; Trottier et al. 2018). The only studies that compare traditional regression models and advanced machine learning methods (also related to the primary market) are Götze et al. (2020) and Makariou et al. (2021). However, compared with the primary market, CAT bond secondary market premia display significantly smaller uncertainty in the sense of conditional variance (given the available price information of the previous points in time).² Consequently, besides the availability of more information due to the panel data structure compared to the primary market, the secondary market for CAT bonds is a low uncertainty environment for which it is still unclear whether the forecasting quality of machine learning methods exceeds the forecasting quality of traditional linear regression. In this respect, the CAT bond secondary market seems to provide an unexplored environment to study the forecasting performance of the procedures.

The literature on the relevant factors influencing CAT bond premia in the secondary market is based on traditional linear regressions. Gürtler et al. (2016) conduct the first study in the secondary market of CAT bonds and show that their premia depend on different bond-specific and macroeconomic factors. Herrmann and Hibbeln (2021, 2022) examine the influence of seasonality and liquidity and Götze and Gürtler (2020) investigate the impact of sponsor characteristics on CAT bond premia in the secondary market. However, the identification and plausibility of the factors influencing CAT bond premia within the framework of machine learning methods are missing for both the secondary and primary markets, making these methods unsuitable so far, at least for the institutional sector, due to the lack of transparency.

Our study is based on a data set comprising all public CAT bond issues conducted in the period between November 1997 and March 2018. The dependent variable is the monthly secondary market price from Aon Benfield between December 2000 and March 2018. The data set is completed using CAT-bond-specific, sponsor-specific, and macroeconomic data. Furthermore, we use the monthly arrival frequencies for US hurricanes and European winter storms to design a measure of seasonality in the CAT bond market. On this basis, we develop the above-mentioned forecasting models for CAT bond premia in the secondary market, which we test using a rolling sample forecast.

The results show that random forest outperforms linear regression and artificial neural network in terms of the sum of squared errors (SSE). This result is confirmed by the Diebold–Mariano (DM) test, in which the difference in performance accuracy is statistically significant. Because we are concerned with the applicability of the best performing method, we pursue the second objective of the study only with the random forest method. Fortunately, approaches to detect variable importance already exist for the random forest. In our study, we used the “number of trees measure” and “node impurity decrease” to determine the importance of the explanatory variables for CAT bond premia. To compare these results with the results of a linear regression, we additionally developed a possibility to identify significant variables within the rolling sample architecture of the study. It turns out that the most important variables for the random forest essentially correspond to the significant variables of the linear regression. In this way, even the effect directions of the important variables can be identified via the linear regression coefficients.

The remainder of this paper is organized as follows. Section 2 describes the data set, including the sample selection approach, variables, and descriptive statistics. In Sect. 3, we describe the model framework and introduce the modeling approaches used. Section 4 presents the empirical analysis and out-of-sample results for the secondary market. In addition, we provide insights into the determination of the relevant explanatory variables in the random forest and present which variables are important in the specific case of the CAT bond secondary market. Section 5 concludes the paper.

2 Data

This section describes the data used to develop the CAT bond secondary market forecasting model. First, we describe the sample selection procedure. Second, the variables used in the empirical analysis are introduced. Third, descriptive statistics of the data are presented.

2.1 Sample selection

The initial data set is based on 617 CAT bonds traded in the secondary market and issued between November 1997 and March 2018. The dependent variable in our analysis corresponds to CAT bonds’ secondary market premia, defined as yield spread over LIBOR, on a monthly basis which are available since December 2000. CAT bond-specific explanatory variables such as expected losses and issue volumes and terms are obtained from Aon Benfield³. Data on trigger mechanisms, insured peril types and locations are obtained from the Artemis Deal Directory⁴ and Aon Benfield. Data on the bonds’ sponsor are provided by Lane Financial LLC⁵ and macroeconomic data are extracted from Bloomberg and Thomson Reuters.

To prepare the data set for subsequent analyses, all observations with missing or implausible data are excluded. The price of bonds that were labeled “distressed” follow the loss-estimation process, because a triggering event and most likely a default has occurred. Therefore, these bonds are excluded from the data set as of the point in time they became distressed. Furthermore, the analysis is restricted to CAT bonds with a time to maturity of at least half a year. The remaining data set consists of 537 bonds with 11,970 observations of premia.

2.2 Variables

The set of variables included in the forecasting models is based on Braun (2016), Gürtler et al. (2016), Götze and Gürtler (2020) and Herrmann and Hibbeln (2022, 2021). We introduce bond-specific, sponsor-specific, macroeconomic, and seasonal variables, as described below.

2.2.1 Bond-specific variables

We include several bond-specific variables. Studies conducted on the primary market have shown, that the Expected Loss (EL) is the most influential determinant of the CAT bond premium (Galeotti et al. 2013; Braun 2016; Gürtler et al. 2016; Trottier et al. 2018). The EL of a CAT bond is calculated by a third-party risk modeling firm, e.g. AIR Worldwide⁶, as the average loss investors can expect over a given time period, divided by the amount of capital invested. In addition to the EL, we incorporate the Spread at Issue and the variables Bond Issue Volume and Total Issue Volume, which represents the natural logarithm of a bond’s issue volume or the total issue volume of all CAT bonds at the time of observation, respectively, and serve as a proxy for bond liquidity. A dummy variable Trigger Indemnity takes the value of one if the bond’s trigger type is indemnity, and zero otherwise. The variable Maturity captures the impact of a bond’s time to maturity at issuance on premia. Similarly, TTM measures the bond’s (remaining) time to maturity at the time of observation. To reflect the complexity of a CAT bond, we include the variables No. of Locations and No. of Perils to account for the number of different insured locations and the number of insured perils, respectively. In addition, we establish a series of dummy variables for different bond rating categories, peril types, and peril locations. Following Gu et al. (2020), we incorporate a momentum factor. Momentum measures the velocity of price changes and is calculated by using the price differences for a fixed time window, as follows:

$$\begin{aligned} \textit{j-month}\ Momentum_{it} = y_{it} - y_{it-j}, \end{aligned}$$

(1)

where $y_{it}$ is the CAT bond premium of bond i at time t. Specifically, the j-month Momentum is positive if the premium of a CAT bond at time t is higher than its premium j months ago. Analogously, a decrease in the premium from time $t-j$ to t leads to a negative momentum value. We consider 1-month, 2-month, 3-month, and 4-month momentums.

2.2.2 Sponsor-specific variables

Present studies show that sponsor characteristics influence CAT bond secondary market premia (Götze and Gürtler 2018, 2020). Consequently, we use the following sponsor-specific variables: Sponsor Diversification, defined as the number of different combinations of peril types and locations insured by CAT bonds of the same sponsor at the observed time and Sponsor Tenure, which describes the tenure of a sponsor (calculated as the difference between the point in time of the first occurrence of the sponsor and the respective observation point in time) and serves as a measure of the sponsor’s experience. The impact of sponsor type on premia is modeled by introducing dummy variables for the sponsor types of Reinsurer, Insurer, and Other. The dummy variable Sponsor Rating NIG takes the value of one for non-investment grade rated sponsors and zero for sponsors with an investment grade rating. Furthermore, we introduce two dummy variables Positive Rating Event and Negative Rating Event based on the sponsor ratings and their placement on the watch list. The variable Positive Rating Event takes a value of one, if (a) the sponsor is upgraded, (b) the sponsor is placed on the watch list for an upgrade, or (c) the sponsor is removed from the watch list for downgrade, and zero otherwise. The definition of Negative Rating Event is analogous.

2.2.3 Macroeconomic variables

Macroeconomic variables are used to consider overall market development in our models. CAT bonds are a potential substitute for traditional reinsurance, suggesting that the prices for these two types of risk transfer instruments show some co-movement (Braun 2016; Gürtler et al. 2016). Therefore, we incorporate the annual relative change in the Guy Carpenter Global Property Catastrophe Rate-on-Line Reinsurance Price Index (Reins. Index), as described in more detail by Carpenter (2012). We use the change in the price index as a proxy for the reinsurance price cycle. We also include Corporate Credit Spread (Corp. Spread), which is based on the credit spread of US corporate bonds of different rating classes and maturities between one and three years, obtained from the Bank of America Merrill Lynch. The variable Corp. Spread is constructed by matching the spreads with bonds in an identical rating class.⁷ Furthermore, we observe the volume-weighted mark-to-market price (weighted price) of outstanding CAT bonds on the secondary market. We then determine the relative change in that price on a monthly basis and label our variable CAT Bond Index, which indicates the investor demand for CAT bonds. By including the Reinsurance Index and the CAT Bond Index, the impact of regulatory changes that may affect the relative attractiveness of CAT bonds is accounted in our models, as both variables are substitutes for risk transfer. In addition, both measures reflect the sponsors’ costs of alternative capital resources, reflecting the current market environment. Finally, we include the monthly returns on the $S \& P \; 500$ to consider equity market development.

2.2.4 Seasonality

For the valuation of CAT bonds insuring hurricanes and winter storms, it is relevant to know how many hurricane or storm seasons fall in the time until maturity of the bond (see e.g. Götze and Gürtler (2020) and Herrmann and Hibbeln (2021)). This seasonality effect is particularly relevant for CAT bonds insuring US hurricanes and European winter storms. Furthermore, bonds that approach maturity, bonds with higher ELs, and single-peril bonds are more strongly influenced by seasonality. Thus, we construct two seasonality variables, considering these aspects. Analogous to Herrmann and Hibbeln (2021), we calculate two different seasonal EL variables for CAT bonds exposed to U.S. hurricanes and European winter storms, respectively. To construct the seasonality measure, we use data on the monthly arrival frequencies of U.S. hurricanes and European winter storms provided by AIR. The seasonally adjusted EL is then calculated based on the initial EL of bond i and monthly arrival frequencies⁸ of catastrophic events $a_{t'}^{Peril}$ as follows:

$$\begin{aligned} EL_{i,t}^{Peril}=I_{[0,1]}(Peril_i) \cdot EL_i \cdot \frac{1}{TTM_{i,t}} \cdot \sum _{t'=t}^{T_i}a_{t'}^{Peril} \end{aligned}$$

(2)

Equation (2) is calculated separately for the US Hurricane and European Winter Storm perils. $TTM_{i,t}$ describes the maturity term of bond i in years. $T_i$ refers to the maturity date of bond i. The indicator function $I_{[0,1]}(Peril_i)$ takes a value of one if the CAT bond insures against the respective peril (US hurricane or European winter storm), and zero otherwise, implying that if a bond does not insure US hurricanes or European winter storms, both seasonal EL variables take a value of zero.

2.3 Descriptive statistics

Table 1 presents the descriptive statistics of the dependent and explanatory variables used in the analysis. All time-invariant variables (EL, Spread at Issue, No. of Perils, No. of Locations, Bond Issue Volume, Maturity, Sponsor type, and the dummy variables for Peril types and locations, bond rating classes, Multiperil, and Trigger Indemnity are reported at the issue level, whereas time-variant variables (seasonal ELs, Total Issue Volume, Sponsor Tenure, Sponsor Diversification, TTM, Momentum variables, the dummy variables for Sponsor Rating NIG, Positive Rating Events and Negative Rating Event, S&P 500, Corp. Spread, Reins. Index, CAT Bond Index) are reported at the observation level. The mean of the premium is $6.74 \%$, which is almost three times greater than the mean of the EL. A bond has an average issue volume of USD 130.69 million and an average maturity of about three years. On average, a CAT bond insures 2 perils and 1.46 locations. Approximately $35 \%$ of CAT bonds in our data set contain an indemnity trigger. Most bonds insure perils such as Earthquakes (EQ) and Hurricanes (HU). The most prevalent peril location is North America (NA). The sponsor type is Reinsurer for $52\%$ of the bonds, whereas the sponsor type is Insurer for $44\%$ of the bonds. Approximately $43\%$ of the CAT bonds have a “BB” rating. The sponsors in the data set have a mean Tenure of about nine years and their mean Diversification is 3.77 peril/location combinations. It is also noticeable that the EL variables and the Spread at Issue show a high correlation with the premium, which may indicate some relevance of the variables in explaining the premium.

Table 1 Summary statistics: CAT-bond-specific, sponsor-specific and macroeconomic variables

3 Model description

In this section, we explain how the forecast quality of the models is determined and how the specific models are implemented. First, we briefly introduce the model framework. Next, we introduce the models used. In this context, we also explain how the required hyperparameters for the respective models are selected.

3.1 Model framework

As explained in the introduction, we consider the CAT bond secondary market because, unlike the primary market, it is subject to much less uncertainty in terms of lower conditional variance. Additionally, the secondary market data set exhibits a much larger sample size than the primary market data set and allows us to include additional explanatory variables that potentially affect the performance of the forecasting models.

All considered models are fitted in-sample and then tested on an out-of-sample period. We fit and test all models in 16 different settings (in-sample/out-of-sample period length combinations) that differ in terms of the length of the in-sample period (one, two, three, or four years) and the length of the out-of-sample period (one, two, three, or four months). After each forecast, we shift each data sample by the length of the out-of-sample period.⁹

Both the in-sample model fit and the out-of-sample forecasting performance are based on the SSE, which is defined as follows (López et al. 2022, p. 400):¹⁰

$$\begin{aligned} SSE = \sum \limits _{i=1}^{m}{(y_{i}-\hat{y}_{i})^{2}}, \end{aligned}$$

(3)

where m is the number of observations in the considered data set, $y_i$ denotes the observed premium of CAT bond i in the data set, and $\hat{y}_{i}$ stands for the estimated premium of bond i.

Because we want to contrast the results of the present secondary market study to the primary market study of Götze et al. (2020), the same forecasting methods (linear regression, random forest, and neural network) are used and examined with respect to their forecasting performance. In the following subsections, we briefly introduce the three price forecasting methods.

3.2 Linear regression model

Empirical models used to forecast the future price of financial assets are mainly based on linear regression models (Campbell and Thompson 2007; Rapach et al. 2010; Thornton and Valente 2012). An advantage of linear regression models is that the economic relationships between the dependent and explanatory variables are easy to interpret, which enables the modeler to identify the causes of poor model performance. This advantage is also exploited in CAT bond literature, as it relies predominantly on linear regression models (Lane 2000; Wang 2000, 2004; Galeotti et al. 2013; Braun 2016; Gürtler et al. 2016). We consider the following linear regression model for the forecast of premia $y_{i,t+1}$ in the secondary market:¹¹

$$\begin{aligned} y_{j,t+1}=\alpha _j+\beta '\cdot V_j+\gamma '\cdot W_{j,t} +\delta '\cdot Z_{j,t+1}+u_{j,t+1} \end{aligned}$$

(4)

for CAT bonds $j=1,\ldots ,n$ and different points in time $t=1,\ldots ,T$. The vector $V_j$ refers to bond-specific variables that are time-invariant, such as the number of insured peril types. Vectors $W_{j,t}$ and $Z_{j,t+1}$ comprise variables that vary by bond and time. Specifically, $Z_{j,t+1}$ contains information on time $t+1$, which is already known at time t, for example seasonality, while $W_{j,t+1}$ refers to time-variant variables, the values of which are not known at time t, such as macroeconomic variables. For this reason, we must draw on $W_{j,t}$ for the prediction of $y_{j,t+1}$. The latter procedure is necessary because a forecast at time t for a variable realization at time $t+1$ may, of course, rely only on information available at time t.

We estimate the linear regression model using the pooled least-squares method. Because this method is standard in economic studies and is intended to serve as a benchmark, we do not discuss this method in more detail. The machine learning methods used are presented in more detail in the following subsections.

3.3 Random forest model

Götze et al. (2020) and Makariou et al. (2021) show that the random forest method represents an adequate approach to forecast CAT bond premia in the primary market. This approach has also been proven to be a good forecasting model for other asset classes (see e.g. Khandani et al. (2010), Mullainathan and Spiess (2017), Gu et al. (2020), Bianchi et al. (2021)). The following brief description of the random forest algorithm, which goes back to Breiman (2001), should provide a better understanding.

With the dependent and independent variables described in Subsection 3.2, we consider the panel data set $\{(y_{j,t+1},V_{j}',W_{j,t}',Z_{j,t+1}')|j=1,\ldots ,n;t=1,\ldots ,T; j$ exists at $t+1\}$. We divide this set into an in-sample data set $S_{IS}$, which covers the points in time $t=1,\ldots ,t^*$ and an out-of-sample data set $S_{OOS}$, which refers to the points in time $t=t^*+1,\ldots ,T$. Consequently, the in-sample data set consists of $k_1\le n\cdot t^*$ elements and the out-of-sample data set of $k_2\le n\cdot (T-t^*)$ elements.¹² With p as the dimension of the vector $(V_{j}',W_{j,t}',Z_{j,t+1}')$ (for arbitrary given j and t) the two subsets can be characterized as follows:¹³

$$\begin{aligned} S_{IS}=\{(y_i,x_{1i},\ldots ,x_{pi})|i=1,\ldots ,k_1\}, \quad S_{OOS}= \{(y_i,x_{1i},\ldots ,x_{pi}))|i=k_1+1,\ldots ,k_1+k_2\}. \end{aligned}$$

(5)

On this basis, the random forest algorithm is divided into five steps:

Step 1: Selection of a randomly chosen subset¹⁴$\{(y_i,x_{1i},\ldots ,x_{pi})|i=1,\ldots ,m\}$ from the in-sample data set.

Step 2: For further procedure, we imagine a tree with a node at the top, from which two edges start, which in turn end at nodes. This node-edge sequences continue downwards. At the top node (the root node), a pre-specified “number of split variables” is selected from the available independent variables $x_1,\ldots , x_p$. For simplicity, we consider the choice of two split variables $x_1$ and $x_2$. For variable $x_1$, a split threshold c is specified, and the data set is split as follows: the data subset $S_A=\{(y_i, x_{1i},\ldots , x_{pi})| x_{1i} > c\}$ (with cardinality $m_A$) is considered on “edge A” and the data subset $S_B=\{(y_i, x_{1i},\ldots , x_{pi})| x_{1i} \le c\}$ (with cardinality $m_B$) is considered on “edge B”. For the edges the following averages are taken as predictions of the dependent variable:

$$\begin{aligned} \bar{y}_{1c}^{(A)}=\frac{1}{m_A}\sum_{\substack{i=1\\x_{1i}>c}}^{m}y_i,\quad \bar{y}_{1c}^{(B)}=\frac{1}{m_B}\sum_{\substack{i=1\\x_{1i}\le c}}^{m}y_i. \end{aligned}$$

(6)

Subsequently, the errors of the two predictions are determined as the respective SSE and the sum of the two errors leads to the “total node error”:

$$\begin{aligned} SSE_{1c} = SSE_{1c}^{(A)}+SSE_{1c}^{(B)} =\sum_{\substack{i=1\\x_{1i}>c}}^{m}(y_i-\bar{y}_{1c}^{(A)})^2 +\sum_{\substack{i=1\\x_{1i}\le c}}^{m}(y_i-\bar{y}_{1c}^{(B)})^2. \end{aligned}$$

(7)

Because this procedure can be performed for an arbitrary threshold $c\in {\mathbb {R}}$, we can also determine the optimal split threshold $c_1^{*}$ leading to the minimum nodal error:

$$\begin{aligned} c_1^{*}=arg \min \limits _{c\in {\mathbb {R}}}(SSE_{1c}). \end{aligned}$$

(8)

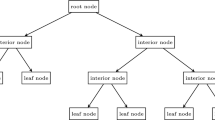
The same procedure is performed for $x_2$ as the split variable, resulting in an optimal split threshold $c_2^{*}$. Without loss of generality let $SSE_{1c_1^{*}}\le SSE_{2c_2^{*}}$, then $x_1$ is the optimal split variable that leads to the smallest SSE with optimal threshold $c_1^{*}$. Thus, $x_1$ becomes the split variable at this node and the edges $A^{*}$ and $B^{*}$ split the initial data set into data subsets $S_{A^{*}}=\{(y_i, x_{1i},\ldots , x_{pi})| x_{1i} > c_1^{*}\}$ and $S_{B^{*}}=\{(y_i, x_{1i},\ldots , x_{pi})| x_{1i} \le c_1^{*}\}$ (see Fig. 1).

Step 3: The procedure in Step 2 is applied to the two subsets, resulting in further edge splits at both edge end nodes. However, in these cases other split variables can be chosen randomly (e.g. $x_3$ and $x_6$ as in Fig. 1), since only the “number of split variables” and not the specific variable selection is given. This procedure is terminated for each end node if either no more splits are performed or the cardinality of a data subset falls below a prespecified minimum $m^{*}$ (the so-called node size).¹⁵ Thus, each resulting end node of the tree “comprises” a data subset with cardinality not lower than $m^{*}$. The arithmetic mean of the remaining (in-sample) values $y_i$ at the corresponding end node represents the premium forecast for all CAT bonds satisfying the respective “splitting path”.

Step 4: As a result of Step 3, the decision tree is used for out-of-sample prediction, i.e. the forecast of $y_i$ given an out-of-sample realization $X_i=(x_{1i},\ldots , x_{pi})$ of the independent variables vector ($i=k_1+1,\ldots ,k_1+k_2$).¹⁶ Specifically, we follow the “splitting path” that this vector satisfies. The premium forecast $\hat{y}_{i}^{(tree\,no.)}$ at the corresponding end node (see Step 3) represents the forecast for $y_i$ (see Fig. 2).

Fig. 1

Construction of a decision tree

Fig. 2

Decision trees forecasts and random forest forecast

Step 5: The entire procedure (Steps 1–4) is repeated for a given number D of decision trees (the so-called number of trees), resulting in a forecast for each tree. Finally, the forecast of the random forest method is the arithmetic mean of all tree forecasts (see Fig. 2).

Because each of the decision trees used in the algorithm is based on a random selection of the data subset and split variables, the trees should be essentially “uncorrelated”. Therefore, in the context of the random forest method, trees are also referred to as decorrelated trees. In summary, based on many randomly chosen in-sample data subsets, the random forest method determines the “best” partitioning of the data subsets in the sense that each subset prediction for y leads to minimal error.

Hyperparameter choice for random forest model

During the description of the procedure it became clear that several parameters (number of split variables, node size, and number of trees) must be specified. These parameters are called hyperparameters and must be chosen optimally with regard to the forecast accuracy. Some parameters are chosen from the literature, and the other parameters are optimized on the respective in-sample data set. To determine the optimal hyperparameter setting (in the so-called tuning process), the three hyperparameters are varied in the random forest procedure to determine the parameter setting that minimizes the forecasting error SSE. In the following, we briefly describe the literature recommendations and tuning methods used for hyperparameter selection.

Number of trees

We varied the number of trees in the grid $\{2, 10, 50, 100, 300, 500, 700\}$. While the numbers 50, 100, 300, 500, and 700 do not imply significant differences in SSE, a number of only 2 or 10 trees leads to a significantly higher SSE. For reasons of comparability to the study of Götze et al. (2020), we set the number of trees to 300 for each model.

Node size

As previously mentioned, node size is a termination criterion of the random forest algorithm. Obviously, a higher value for the node size leads to smaller trees and consequently, a faster termination of the algorithm. For regression problems (i.e., a continuous dependent variable y), the recommended node size value is five (Breiman 2001), which we use in our analysis.

Number of split variables

The number of split variables is the most important hyperparameter for random forest because it strongly affects its performance (Berk 2008). A common approach for tuning hyperparameters is k-fold cross-validation. This method simulates forecast accuracy measurements within the in-sample data set. For this purpose, the in-sample data set is divided into k subsets, of which the union of $k-1$ parts serves as the training data set and the remaining part serves as the test data set. Based on the training data set, the random forest model is applied with a specific hyperparameter realization, and the SSE of the resulting forecast in the test data set is determined. This procedure is repeated with the other $k-1$ possible test data subsets and the average SSE of the resulting k forecasts is determined. Finally, by varying the hyperparameter, the parameter value that leads to the minimum average SSE can be determined. A disadvantage of cross-validation for time series data is the destruction of the time structure by swapping the training and test data sets, which partially leads to the prediction of past data using future data. Therefore, traditional cross-validation is unsuitable for time-series data.

We apply a cross-validation approach adjusted to time series and propsed by Hyndman (2014). This approach avoids using future observations to make past predictions by considering the time structure when splitting the data into training and test data sets. Specifically, in the present study, each training data set consists of 100 observations, and the test data set consists of 42 subsequent observations that approximately corresponds to a 70:30-split ratio. After determining the test SSE, the test-training data sample is shifted by the length of the training data set and the procedure is repeated. As in the general k-fold cross-validation procedure, the optimal hyperparameter value is determined by the variation in the parameter “number of splits”. The variation follows a “grid search,” where the number of splits passes through all numbers between 1 and $p-p_{const}$.¹⁷

Table 2 presents a summary of the hyperparameter values selected in this study.

3.4 Neural network model

Neural networks have produced good forecasting results for various asset classes (Khandani et al. 2010; Mullainathan and Spiess 2017; Gu et al. 2020). In contrast, neural networks showed worse forecasting performance in predicting premia for CAT bonds in the primary market (see Götze et al. (2020)). For better understanding, we first describe the main elements of the neural network method.¹⁸

Analogous to the presentation of the random forest model, we consider the in-sample data set with $k_1$ observations $X_i=(y_i,x_{1i},\ldots ,x_{pi})$ $(i=1,\ldots ,k_1)$ containing the dependent variable y and independent variables $x_1$,..., $x_p$. As in a linear regression, a class of functions $f(X,{\mathbb {B}})$ is considered, which depends on the parameter matrix ${\mathbb {B}}$. This parameter matrix is determined such that $f(X,{\mathbb {B}})$ optimally approximates the dependent variable y. More precisely, the neural network model consists of the following elements.

$\ell$-layer neural network

An $\ell$-layer neural network is a function $f:{\mathbb {R}}^p \rightarrow {\mathbb {R}}^q$, which is a composition of $\ell$ functions $f_j$ $(j=1,\ldots ,\ell )$, where p is the dimension of the input $X=(x_1,\ldots ,x_p)$ (the independent variables) and q is the dimension of the output y:¹⁹

$$\begin{aligned} f = f_{\ell }\circ ... \circ f_2 \circ f_1, \hbox {i.e}.\ f(X)=f_{\ell }( ... (f_2(f_1(X))) ... ) \ \hbox {for}\; \ X=(x_1,...,x_p). \end{aligned}$$

In this context, $f_j:{\mathbb {R}}^{p_{j-1}} \rightarrow {\mathbb {R}}^{p_{j}}$ denotes the so-called j-th layer, where $p_{j-1}$ is the input dimension of layer j and $p_{j}$ is the corresponding output dimension for all $j=1,\dots ,\ell$ implying $p_0=p$ and $p_{\ell }=q$. Further, $f_{\ell }$ stands for the output layer, whose application to the rest of the function chain leads to the output, that is, the estimation of y. Since the outputs of the “inner” functions $f_1$,..., $f_{\ell -1}$ are not visible, these functions are called hidden layers. The number $\ell -1$ of hidden layers (or the so-called depth $\ell$ of the “deep” neural network) and the dimensions $p_j$ of the layer output (the so-called width of the layer) are hyperparameters that have to be prespecified.

Design of the layer functions

The layers are transformed affine functions of the form $f_j(X_j) = g_j(\beta _{0j} +B_j\cdot X_j)$ with $X_j\in {\mathbb {R}}^{p_{j-1}}$ the layer input, $\beta _{0j}\in {\mathbb {R}}^{p_j}$ a constant vector (so-called bias) and $B_j\in {\mathbb {R}}^{p_{j}\times p_{j-1}}$ a matrix of coefficients (so-called weights). $g_j:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is a continuous, monotonically increasing function called the activation function. This function is applied element-wise to the output vector of the affine function. Typical activation functions are the logistic function, the hyperbolic tangent function, and the rectified linear unit (ReLU) function.²⁰.

Connection to a neural network

From the composition of several functions it is not immediately comprehensible why this should be an (artificial) neural network. In this context, the vector of each layer can be considered as a collection of neurons. Each vector component can be interpreted as a neuron in the sense that it receives inputs from other neurons, weights these inputs, determines an activation value, and passes this on as an output to other neurons. In the present case, information flows are always passed in one direction (i.e., from layer $j-1$ to layer j), and the resulting network is called a feedforward neural network. A visualization of such a network is shown in Fig. 3.

Fig. 3

The j-th layer in a neural network

Forecast procedure with a neural network

First, we select the in-sample data set $\{(y_i,x_{1i},\ldots ,x_{pi})|i=1,\ldots ,k_1\}$. For a randomly given set of parameters $\beta _{0j}$ and $B_j$ $(j=1,\ldots ,\ell )$ the forecast of $y_i$ is determined as $\hat{y}_i=f_{\ell }(... (f_2(f_1(x_{1i},\ldots ,x_{pi})))$ for all $i=1,\ldots ,k_1$. As with the random forest method, we assess the forecast error based on the SSE,

$$\begin{aligned} SSE_{NN} = \sum _{i=1}^{k_1}(y_i-\hat{y}_{i})^2. \end{aligned}$$

(9)

Subsequently, the parameter set $\beta _{0j}$ and $B_j$ $(j=1,\ldots ,\ell )$ is adjusted to lead to the minimum prediction error:

$$\begin{aligned} {\mathbb {B}}^{*}=(\beta _{01}^{*},B_1^{*},\ldots ,\beta _{0\ell }^{*}, B_{\ell }^{*})= arg \min \limits _{\begin{array}{c} \beta _{0j}\in {\mathbb {R}}^{p_j},\\ B_j\in {\mathbb {R}}^{p_j}\times {\mathbb {R}}^{p_{j-1}},\\ j=1,\ldots ,\ell \end{array}}(SSE_{NN}). \end{aligned}$$

(10)

The minimum (10) is typically determined numerically. In this context, the gradient-descent procedure is a common numerical method. The necessary computation of the gradients is usually performed using the so-called backpropagation algorithm.²¹ To determine the minimum ${\mathbb {B}}^{*}$ based on a starting matrix ${\mathbb {B}}_0$, the gradient descent method generates a sequence of points ${\mathbb {B}}_{j}$ according to the iteration rule

$$\begin{aligned} {\mathbb {B}}_{j+1}={\mathbb {B}}_{j}+\eta _j \cdot \nabla SSE_{NN}({\mathbb {B}}_{j}), \end{aligned}$$

(11)

where $\nabla SSE_{NN}({\mathbb {B}}_{j})$ stands for the gradient of the error function and $\eta _{j}$ is a prespecified step size, the so-called learning rate. In this way, the parameter matrix ${\mathbb {B}}$ is adjusted in the direction of the steepest descent of the error function. A termination condition for the iteration is a gradient lower than a prespecified threshold (i.e., the gradient is nearly zero).

Finally, we apply the optimally tuned function $f(X,{\mathbb {B}}^{*})$ to predict $y_i$ given an out-of-sample realization $X_i=(x_{1i},\ldots , x_{pi})$ ($i\in \{k_1+1,\ldots , k_1+k_2\}$) of the independent variables vector according to $\hat{y}_i=f(X_i,{\mathbb {B}}^{*})$.

Hyperparameter choice for the neural network model

In the following, we provide an overview of the hyperparameters introduced above that must be determined for a neural network and explain how we specify their respective values. The parameters to be tuned include the number of hidden layers, width of each hidden layer, learning rate, and gradient threshold. Furthermore, the activation function must be specified.

Error threshold

As mentioned above, the gradient descent method requires a threshold below which the gradient leads to termination of the gradient descent procedure. On the one hand, a low threshold value should be chosen so that the prediction errors are as small as possible. On the other hand, a low threshold value increases the running time of the neural network algorithm tremendously. In summary, the error threshold must be carefully selected considering two conflicting objectives, and depends on the dependent variable of the study. Since the CAT bond premium is a relative variable that should be predicted as accurately as possible (in a tolerable time), we choose a threshold of $10^{-4}$.

Number and width of hidden layers

With respect to the running time, we abstain from tuning the number of hidden layers and use three hidden layers throughout all time periods of our rolling sample approach. This choice of three hidden layers has achieved good results in several studies (Shen et al. 2021; Gu et al. 2020). In contrast, to tune the width of each hidden layer (based on the respective in-sample data set), we use a grid search approach in which we pass through all width combinations $(i,j,l)\in \{1,4,\ldots ,34\}\times \{1,4,\ldots ,28\}\times \{1,4,\ldots ,16\}$ for all three hidden layers.

Activation function

In the present approach, we use the logistic function $g(x)=1/(1+e^{-x})$ as the activation function, which is common and recommended (Hastie et al. 2017, p. 392).

Training algorithm and learning rate

The choice of a constant learning rate $\eta _j$ as described in the basic version of the gradient descent method often leads to a poor convergence to the minimum. Against this background, we use a variation of the basic version, the so-called resilient backpropagation of (Riedmiller and Rprop 1994). In this variant, the learning rate is dynamically adjusted for each dimension via an iterative procedure. For the iterations, two initial learning rates are randomly chosen. In the next iteration step, the preceding learning rate is multiplied by a high factor a or a low factor b depending on the sign of the gradient. Furthermore, to limit the resulting learning rate, an upper bound $\eta _{max}$ and a lower bound $\eta _{min}$ are given. Thus, instead of a constant learning rate as a hyperparameter, resilient backpropagation requires the specification of the learning rate factors a and b and the learning rate limits $\eta _{max}$ and $\eta _{min}$. In the present study, we use the default parameters of (Fritsch et al. 2019): $a=1.2$, $b=0.5$, $\eta _{min}=10^{-6}$, and $\eta _{max}=0.1$.

A summary of the selected hyperparameter values for both the random forest and neural network is presented in Table 2.

Table 2 Selection of hyperparameter values for random forest and neural network model

4 Empirical analysis

4.1 Out-of-sample results and performance evaluation

This section presents the results of the empirical analysis. For the secondary market data set, Table 3 shows the performance of the linear regression, random forest, and neural network models in the out-of-sample forecast measured by the mean SSE.²² The first row (column) reports the in-sample (out-of-sample) periods of the rolling sample analysis.

The results show that for the linear regression model, the combination of a one year in-sample period and a one month out-of-sample period yields the best forecasting result in terms of a mean SSE of 0.0219. The mean SSE increases with an increase in the out-of-sample period, which is not surprising as the uncertainty in the data also increases when extending the out-of-sample period. The mean SSE also increases when extending the in-sample period, which is possibly due to the fact, that less recent information (in the extended in-sample period), on average, provides less accurate estimates of future prices (in the out-of-sample period).

In terms of mean forecasting performance, the random forest dominates the linear regression and neural network for each combination of in-sample and out-of-sample period lengths. Similar to the linear regression, the random forest also exhibits the lowest mean SSE of 0.0133 for the one-year in-sample/one-month out-of-sample forecasting constellation, and the SSE tends to increase with an increase in the in-sample period and out-of-sample period.

Interestingly, the neural network behaves differently from the other two methods. The results show that for the neural network model, the combination of a four-year in-sample period and a one-month out-of-sample period yields the best forecasting result with a mean SSE of 0.0428. However, the mean SSE of the neural network does not exhibit a regular pattern when the in-sample period is increased. Consequently, the results do not allow any conclusions in terms of neural networks performing better with more input data. The results show that in all in-sample/out-of-sample period length combinations, neural networks perform worse than random forest and linear regression in terms of mean SSE.

Table 3 Out-of-sample performance on the secondary market data set

To assess the statistical significance of the performance differences, we follow Bianchi et al. (2021) and additionally consider the p-value of the one-sided DM test (Diebold and Mariano 1995) with the Harvey-Leybourne-Newbold correction (Harvey et al. 1997). Under the assumption that the random forest outperforms the linear regression model, we test the null hypothesis of no performance differences against the alternative hypothesis that random forest forecasts are more accurate than linear regression forecasts.²³ We calculate the DM test for every in-sample/out-of-sample combination, defining h as the forecasting horizon in months and receiving multiple test statistics for longer out-of-sample periods. For the respective in-sample/out-of-sample combinations, we obtain p-values for the DM statistics and calculate the median over these p-values to present the results in Table 4.

Table 4 Significance of Performance Differences between the Random Forest and Linear Regression Model on the Secondary Market Dataset

The null hypothesis is rejected at the 5% level for 22 (out of 40) in-sample/out-of-sample period length combinations and even for 35 periods at the 10% level. The p-values tend to increase with longer forecasting horizons h for the different in-sample/out-of-sample period length combinations, which suggests that random forest forecasts are more susceptible to increasing the forecasting horizon than linear regression forecasts. Thus, the DM test results are in line with the SSEs in Table 3, which also indicate decreasing performance differences with increasing out-of-sample periods. Overall, the results show that the random forest forecasts not only appear to be more accurate in terms of mean SSE, but also significantly outperform the linear regression forecasts.

As a recommendation for action in the context of forecasting CAT bond premia, it can be stated that, regardless of the considered market environment, the random forest method provides the significantly best forecasting results. To be able to use the “forecast winner” random forest in (institutional) practice, it still needs to be clarified how a certain transparency of the procedure can be achieved. This is the subject of the following subsection.

4.2 Variable importance

As mentioned in the introduction, a central point of criticism of machine learning methods is the black-box nature, which contradicts usual transparency requirements that, e.g., regulators are demanding for institutional investors. To achieve transparency and interpretability of the random forest results, we use the available variable importance measures to describe the determinants of CAT bond premia identified by the random forest model. To assess the results, we compare the identified important variables with the variables that are significant (at the upper quartile) in the linear regression model.

Specifically, we determine two measures of variable importance for each random forest model. First, we consider the number of trees measure, which describes the total number of trees in which a split occurs on a certain variable (Paluszynska et al. 2020).²⁴ Thus, a higher number of trees measure implies higher importance of a variable. Second, we analyze the node impurity decrease, which describes the total decrease in node impurity from splitting on a certain variable, averaged over all trees of the random forest. In this study, the decrease in node impurity is measured based on the difference between the SSE before and after splitting on a certain variable. A higher impurity decrease can be interpreted as a higher importance of the respective variable as it indicates a higher contribution to reducing SSE.

To interpret the variable importance results, both the number of trees measure and node impurity decrease are averaged for each in-sample/out-of-sample period length combination. The results can be seen in Figs. 4 and 5. In addition, to analyze variable importance from the linear regression results, we calculate the upper quartile of p-values for each variable and every in-sample/out-of-sample period length combination. The corresponding results are shown in Fig. 6.²⁵

Figure 4 shows the results based on the number of trees measure. The literature does not provide a clear recommendation regarding when a variable can be considered important in terms of the number of trees measure relative to the number of trees built for training. However, for each forecast combination, we observe a certain group of variables that is used in (almost) every tree, before the number of trees measure decreases continuously across the variables that appear to be less relevant for the premium forecast. Because the literature does not specify a threshold for the number of trees measure above which a variable is considered important, we set a threshold of 292.5 out of 300 trees (i.e., 97.5 %) for this study. For the one-year in-sample period, the bond-specific variables Time to Maturity, Maturity, EL, both seasonal EL variables, Spread at Issue, all four Momentum variables, Bond Issue Volume, Total Issue Volume, Sponsor Tenure, and the macroeconomic variables Corporate Spread, CAT Bond Index, and S&P 500 exhibit a high importance in terms of the number of trees measure. These results complement existing studies using linear regression, showing that EL is the most influential variable in CAT bond premia (Galeotti et al. 2013; Gürtler et al. 2016; Trottier et al. 2018). Additionally, the high variable importance of the seasonality measures supports the linear regression results of Herrmann and Hibbeln (2021). The importance of the macroeconomic variables is in line with the results of Braun (2016), Gürtler et al. (2016), Götze et al. (2020). For the 2 year in-sample period, Fig. 4 shows that the Reinsurance Index and Sponsor Diversification have high variable importance, which is consistent with results of Götze and Gürtler (2018, 2020). Neither the three- nor the four-year in-sample periods produce substantially new results. A minor difference compared to the shorter in-sample periods can be seen in the fact that the variables Number of Perils and Earthquake are considered as important for longer in-sample periods. This is because trees become larger with larger in-sample periods, which in turn leads to an increase in the number of trees measure for almost all variables. For the variables Number of Perils and Earthquake, this increase results in exceeding the threshold of 292.5.

Fig. 4

Number of trees measure. This figure shows the importance of the variables using the number of trees measure. A value of 300 implies the considered variable is used as splitting criterion in every tree

Fig. 5

Node impurity decrease measure. This figure shows the importance of the variables using the node purity measure. A high value indicates higher importance of a variable

Figure 5 shows the results based on the node impurity decrease measure. This confirms the results of the number of trees measure. In particular, the Spread at Issue, EL, and $EL^{US HU}$ exhibit high importance. Although the literature does not indicate a threshold for the node impurity decrease that constitutes an important variable, we can use the ranking based on this measure to assess the variables’ relative importance. After the three aforementioned variables, Fig. 5 shows a large gap in the decrease in node impurity. However, the importance ranking of the following variables is consistent across all considered in-sample periods: Corporate Spread, $EL^{EU Wind}$, 4-month Momentum, Reins. Index, TTM, and Sponsor Tenure. Therefore, these variables can be considered important for CAT bond premium forecasts. Additionally, they largely correspond to those that are already identified as important by the number of trees measure.

The variable importance resulting from the linear regression model are shown in Fig. 6. In this context, the importance of a variable is measured by the upper quartile of its p-values of the respective in-sample/out-of-sample period length combination.²⁶ Accordingly, Fig. (a) shows that 5 variables are significant (with $p\le 0.05$). The number of significant variables increases with the length of the out-of-sample data set. In Fig. (d), 14 variables are significant. The linear regression detects the highly significant variables that are already reported by the importance measures of the random forest (e.g., Spead at Issue, 4-month Momentum, $EL^{US HU}$, EL). Interestingly, the regions Japan, North America, and Europe appear among the most relevant influences obtained from the linear regression model, but do not show high relevance referring to the random forests’ variable importance measures. However, because the random forest predicts CAT bond premia more precise than linear regression, we place greater confidence in the variable selection by the random forest than by linear regression. In this way, the variable importance results complement the previous regression-based literature.

Fig. 6

Linear regression p-values. This figure shows the importance of the variables evaluating their significance in terms of the p-value. In contrast to the node impurity decrease measure, a low p-value indicates high importance of a variable

However, it can also be noted that the identified variables of highest significance (e.g., Spread at Issue, EL, seasonal ELs, Reins. Index) are consistent with the results of previous linear regression studies as well as with the most important variables identified by random forest. Moreover, our analyses show that the included momentum variables are determinants of the CAT bond secondary market. In this context, an interesting finding is that the 4-month Momentum variable shows the greatest influence among all momentum variables in terms of all three variable importance measures. It might be interesting for further studies to analyze the impact of these variables in more detail.

Altogether, the variable importance results shown in Figs. 4 and 5 indicate that the random forest models not only achieve precise forecasting results, but also that the most relevant out-of-sample predictors of CAT bond secondary market premia are in line with the variables identified using linear regressions and, moreover, even reveal new relationships.

A disadvantage of the importance measures is the lack of possibility to measure the direction of variable influences. At least for the variables identified as relevant in both the random forest and the linear regression, we examine the effect direction using the regression coefficients. However, due to the rolling sample architecture of the study, a large number of coefficients are available for the respective variables. Against this background, we examined the distribution of positive or negative influences of the relevant variables in Table 5.

Table 5 Direction of the variables’ influences

Specifically, for each relevant variable, we reported the proportion of models in which the respective variable has the corresponding sign among the models in which that variable is significant. E.g., the Spread at Issue and the 4-Month Momentum have positive regression coefficients in every model in which they are significant. This means, a higher Spread at Issue (4-month Momentum) corresponds to a higher CAT bond premium.

5 Conclusion

On the one hand, recent studies have shown that advanced machine learning methods turn out to be particularly successful in predicting asset prices. On the other hand, traditional linear regression is easier to interpret than most machine learning methods, which is an important property since regulatory requirements imply transparency. Therefore, the motivation of the present study was to investigate the forecasting accuracy of such methods and to determine the possibility of identifying explanatory determinants when applying machine learning methods. Specifically, we analyzed the secondary market for CAT bonds, for which a large number of influencing variables exists that can be taken into account in price forecasting using machine learning methods. For example, random forest has already produced promising results in the literature for price forecasting in the CAT bond primary market. Because the secondary market has additional explanatory determinants compared to the primary market (such as the historical price change of premia), the results from the primary market cannot simply be transferred to the secondary market.

For this purpose, three different forecasting approaches were compared. As representatives of advanced machine learning methods, the random forest and artificial neural network models were implemented and contrasted with traditional linear regression. Based on the mean SSE (and mean RMSE), the random forest model provides better forecasting performance than the linear regression and neural network approaches. In addition, the DM test indicates that the outperformance of the random forest model is significant.

However, even if the random forest leads to better forecasting results than linear regression, it is particularly relevant for institutional investors that the forecasting method used has transparency with regard to the relevant influencing parameters of the model. Because this form of transparency is a considerable advantage of linear regression, it remained to be determined how to identify the influencing parameters in a random forest model.

Based on the number of trees measure and node impurity decrease, we find the highest relevance of the variables Spread at Issue, EL, and $EL^{USHU}$, which seems plausible against the background of previous (regression) studies. We additionally contrasted these “relevance results” for the random forest with the “significance results” of the linear regression, for which the variables with the highest relevance are confirmed. Based on the regression results, we were additionally able to identify the direction of effect of the most important variables.

In summary, the present study contributes to the asset pricing literature by showing that the use of machine learning methods can lead to significantly higher forecasting accuracy of CAT bond premia. Consequently, the application of random forest can be useful to practitioners involved with the trading of CAT bonds in the secondary market. Through improved price forecasting, investors identify overvalued and undervalued securities, which in turn leads to better buy and sell decisions. The additional ability to identify the effect direction of important variables on CAT bond pricing also allows investors to pay particular attention to these variables.

In addition to decision support, the findings contribute to the general understanding of the price determinants of CAT bonds in the secondary market.