Skip to main content
SpringerLink
Log in

Detections of bifurcation in a fractional-order Cohen-Grossberg neural network with multiple delays

  • Research Article
  • Published:
Cognitive Neurodynamics Aims and scope Submit manuscript

Abstract

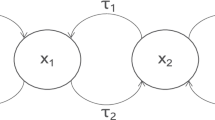
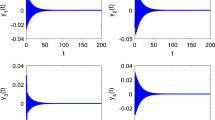
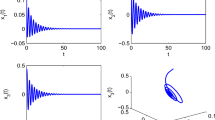
The dynamics of integer-order Cohen-Grossberg neural networks with time delays has lately drawn tremendous attention. It reveals that fractional calculus plays a crucial role on influencing the dynamical behaviors of neural networks (NNs). This paper deals with the problem of the stability and bifurcation of fractional-order Cohen-Grossberg neural networks (FOCGNNs) with two different leakage delay and communication delay. The bifurcation results with regard to leakage delay are firstly gained. Then, communication delay is viewed as a bifurcation parameter to detect the critical values of bifurcations for the addressed FOCGNN, and the communication delay induced-bifurcation conditions are procured. We further discover that fractional orders can enlarge (reduce) stability regions of the addressed FOCGNN. Furthermore, we discover that, for the same system parameters, the convergence time to the equilibrium point of FONN is shorter (longer) than that of integer-order NNs. In this paper, the present methodology to handle the characteristic equation with triple transcendental terms in delayed FOCGNNs is concise, neoteric and flexible in contrast with the prior mechanisms owing to skillfully keeping away from the intricate classified discussions. Eventually, the developed analytic results are nicely showcased by the simulation examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  • Aslipour Z, Yazdizadeh A (2019) Identification of nonlinear systems using adaptive variable-order fractional neural networks (Case study: A wind turbine with practical results). Eng Appl Artif Intell 85:462–473

    Article  Google Scholar 

  • Cao JD, Manivannan R, Chong KT, Lv XX (2019) Enhanced \(L_2\)-\(L_\infty\) state estimation design for delayed neural networks including leakage term via quadratic-type generalized free-matrix-based integral inequality. J Franklin Inst 356:7371–7392

    Article  Google Scholar 

  • Chen YP, Fu ZM, Liu YR, Alsaadi Fuad E (2017) Further results on passivity analysis of delayed neural networks with leakage delay. Neurocomputing 224:135–141

    Article  Google Scholar 

  • Chen LP, Yin H, Huang TW, Yuan LG, Zheng S, Yin LS (2020) Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw 125:174–184

    Article  PubMed  Google Scholar 

  • Cohen MA, Grossberg S (1983) Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. Adv Psychol 42:288–308

    Google Scholar 

  • Dalir M, Bashour M (2010) Applications of fractional calculus. Appl Math Sci 4:1021–1032

    Google Scholar 

  • Deng WH, Li CP, Lü JH (2007) Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn 48:409–416

    Article  Google Scholar 

  • Du FF, Lu JG (2022) New results on finite-time stability of fractional-order Cohen-Grossberg neural networks with time delays. Asian J Control 24:2328-2337

    Article  Google Scholar 

  • Gopalsamy K (2007) Leakage delays in BAM. J Math Anal Appl 325:1117–1132

    Article  Google Scholar 

  • Gu YJ, Yu YG, Wang H (2017) Synchronization-based parameter estimation of fractional-order neural networks. Phys A 483:351–361

    Article  Google Scholar 

  • Hashemizadeh E, Ebrahimzadeh A (2018) An efficient numerical scheme to solve fractional diffusion-wave and fractional Klein-Gordon equations in fluid mechanics. Phys A 503:1189–1203

    Article  Google Scholar 

  • Haubold H, Mathai A (2017) An introduction to fractional calculus. Nova Science, New York

  • Huang CD, Cao JD (2018) Impact of leakage delay on bifurcation in high-order fractional BAM neural networks. Neural Netw 98:223–235

    Article  PubMed  Google Scholar 

  • Huang CD, Cao JD, Ma ZJ (2016) Delay-induced bifurcation in a tri-neuron fractional neural network. Int J Syst Sci 47:3668–3677

    Article  Google Scholar 

  • Huang CD, Wang J, Chen XP, Cao JD (2021) Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw 141:344–354

    Article  PubMed  Google Scholar 

  • Huang CD, Liu H, Chen YF, Chen XP, Song F (2021) Dynamics of a fractional-order BAM neural network with leakage delay and communication delay. Fractals 29:2150073

    Article  Google Scholar 

  • Huang CD, Cao JD (2022) Bifurcations due to different delays of high-order fractional neural networks. Int J Biomath 15:2150075

    Article  Google Scholar 

  • Jafari M, Kheiri H, Jabbari A (2021) Backward bifurcation in a fractional-order and two-patch model of tuberculosis epidemic with incomplete treatment. Int J Biomath 14:2150007

    Article  Google Scholar 

  • Jia J, Huang X, Li YX, Cao JD, Alsaedi A (2020) Global stabilization of fractional-order memristor-based neural networks with time delay. IEEE Trans Neural Netw Learn Syst 31:997–1009

    Article  PubMed  Google Scholar 

  • Ke YQ, Miao CF (2015) Stability analysis of fractional-order Cohen-Grossberg neural networks with time delay. Int J Comput Math 92:1102–1113

    Article  Google Scholar 

  • Kumar S, Zeidan D (2022) Numerical study of Zika model as a mosquito-borne virus with non-singular fractional derivative. Int J Biomath 15:2250018

    Article  Google Scholar 

  • Li ZY, Zhang YH (2022) The boundedness and the global Mittag-Leffler synchronization of fractional-order inertial Cohen-Grossberg neural networks with time delays. Neural Process Lett 54:597–611

    Article  Google Scholar 

  • Li XD, Fu XL, Rakkiyappan R (2014) Delay-dependent stability analysis for a class of dynamical systems with leakage delay and nonlinear perturbations. Appl Math Comput 226:10–19

    Article  Google Scholar 

  • Li HL, Jiang HJ, Cao JD (2020) Global synchronization of fractional-order quaternion-valued neural networks with leakage and discrete delays. Neurocomputing 385:211–219

    Article  Google Scholar 

  • Luo YT, Zhang L, Teng ZD, Zheng TT (2021) Stability and bifurcation for a stochastic differential algebraic Holling-II predator-prey model with nonlinear harvesting and delay. Int J Biomath 14:2150019

    Article  Google Scholar 

  • Naik PA, Zu J, Naik MUD (2021) Stability analysis of a fractional-order cancer model with chaotic dynamics. Int J Biomath 14:2150046

    Article  Google Scholar 

  • Podlubny I (1999) Fractional differential equations. Academic Press, New York

    Google Scholar 

  • Popa CA (2020) Dissipativity of impulsive matrix-valued neural networks with leakage delay and mixed delays. Neurocomputing 405:85–95

    Article  Google Scholar 

  • Pratap A, Raja R, Cao JD, Lim CP, Bagdasar O (2019) Stability and pinning synchronization analysis of fractional order delayed Cohen-Grossberg neural networks with discontinuous activations. Appl Math Comput 359:241–260

    Google Scholar 

  • Rajivganthi C, Rihan FA, Lakshmanan S, Muthukumar P (2018) Finite-time stability analysis for fractional-order cohen Grossberg BAM neural networks with time delays. Neural Comput Appl 29:1309–1320

    Article  Google Scholar 

  • Shiri B, Baleanu D (2022) A general fractional pollution model for lakes. Com Appl Math Comput 4:1105–1130

    Google Scholar 

  • Shiri B, Wu GC, Baleanu D (2020) Collocation methods for terminal value problems of tempered fractional differential equations. Appl Numer Math 156:385–395

    Article  Google Scholar 

  • Shiri B, Wu GC, Baleanu D (2021) Terminal value problems for the nonlinear systems of fractional differential equations. Appl Numer Math 170:162–178

    Article  Google Scholar 

  • Syed Ali M, Narayanan G, Shekher V, Alsulami H, Saeed T (2020) Dynamic stability analysis of stochastic fractional-order memristor fuzzy BAM neural networks with delay and leakage terms. Appl Math Comput 369:124896

    Google Scholar 

  • Tang BN (2020) Bifurcation study on fractional-order Cohen-Grossberg neural networks involving delays. Math Probl Eng 2020:8833366

    Article  Google Scholar 

  • Tian XH, Xu R (2017) Stability and Hopf bifurcation of time fractional Cohen-Grossberg neural networks with diffusion and time delays in leakage terms. Neural Process Lett 45:593–614

    Article  Google Scholar 

  • Tian XH, Xu R (2017) Stability and Hopf bifurcation of a delayed Cohen-Grossberg neural network with diffusion. Math Methods Appl Sci 40:293–305

    Article  Google Scholar 

  • Wang LM, Song QK, Liu YR, Zhao ZJ, Alsaadi Fuad E (2017) Finite-time stability analysis of fractional-order complex-valued memristor-based neural networks with both leakage and time-varying delays. Neurocomputing 245:86–101

    Article  Google Scholar 

  • Wan LG, Liu ZX (2021) Multiple O(t^{-q}) stability and instability of time-varying delayed fractional-order Cohen-Grossberg neural networks with Gaussian activation functions. Neurocomputing 454:212–227

    Article  Google Scholar 

  • Wouapi MK, Fotsin BH, Ngouonkadi EBM, Kemwoue FF, Njitacke ZT (2021) Complex bifurcation analysis and synchronization optimal control for Hindmarsh-Rose neuron model under magnetic flow effect. Cogn Neurodyn 15:315–347

    Article  PubMed  Google Scholar 

  • Wu RC, Hei XD, Chen LP (2013) Finite-time stability of fractional-order neural networks with delay. Commun Theor Phys 60:189–193

    Article  Google Scholar 

  • Xu CJ, Tang XH, Liao MX (2011) Stability and bifurcation analysis of a six-neuron BAM neural network model with discrete delays. Neurocomputing 74:689–707

    Article  Google Scholar 

  • Xu CJ, Aouiti C, Liu ZX (2020) A further study on bifurcation for fractional order BAM neural networks with multiple delays. Neurocomputing 417:501–515

    Article  Google Scholar 

  • Yang G, Shiri B, Kong H, Wu GC (2021) Intermediate value problems for fractional differential equations. Comput Appl Math 40:195

    Article  Google Scholar 

  • Zhang FH, Zeng ZG (2021) Multiple Mittag-Leffler stability of delayed fractional-order Cohen-Grossberg neural networks via mixed monotone operator pair. IEEE Trans Cybern 51: 6333–6344

    Article  PubMed  Google Scholar 

  • Zhang LZ, Yang YQ, Xu XY (2018) Synchronization analysis for fractional order memristive Cohen-Grossberg neural networks with state feedback and impulsive control. Phys A 506:644–660

    Article  Google Scholar 

Download references

Acknowledgements

This work was jointly supported by the Youth Research Fund Project of Xinyang Normal University under Grant No.2022-QN-044 and the Nanhu Scholars Program for Young Scholars of Xinyang Normal University and Graduate Research and Innovation Fund Project of Xinyang Normal University under Grant No.2021KYJJ47.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xinyang Normal University, Xinyang, 464000, China

    Chengdai Huang & Shansong Mo

  2. School of Mathematics, Southeast University, Nanjing, 210096, China

    Jinde Cao

  3. Yonsei Frontier Lab, Yonsei University, Seoul, 03722, South Korea

    Jinde Cao

Authors
  1. Chengdai Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shansong Mo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinde Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chengdai Huang.

Ethics declarations

Conflict of interest

We declare that we have no conflict of any financial and personal relationships with other people and organizations.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, C., Mo, S. & Cao, J. Detections of bifurcation in a fractional-order Cohen-Grossberg neural network with multiple delays. Cogn Neurodyn 18, 1379–1396 (2024). https://doi.org/10.1007/s11571-023-09934-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11571-023-09934-2

Keywords

Search

Navigation