Skip to main content
SpringerLink
Log in

Randomized policy of a poisson input queue with J vacations

  • Published:
Journal of Systems Science and Systems Engineering Aims and scope Submit manuscript

Abstract

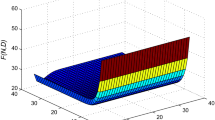
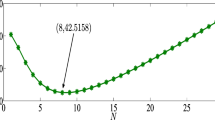
This paper studies the operating characteristics of an M/G/1 queuing system with a randomized control policy and at most J vacations. After all the customers are served in the queue exhaustively, the server immediately takes at most J vacations repeatedly until at least N customers are waiting for service in the queue upon returning from a vacation. If the number of arrivals does not reach N by the end of the J th vacation, the server remains idle in the system until the number of arrivals in the queue reaches N. If the number of customers in the queue is exactly accumulated N since the server remains idle or returns from vacation, the server is activated for services with probability p and deactivated with probability (1 − p). For such variant vacation model, other important system characteristics are derived, such as the expected number of customers, the expected length of the busy and idle period, and etc. Following the construction of the expected cost function per unit time, an efficient and fast procedure is developed for searching the joint optimum thresholds (N*, J*) that minimize the cost function. Some numerical examples are also presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Arumuganathan, R. & Jeyakumar, S. (2005). Steady state analysis of a bulk queue with multiple vacations, setup times with N-policy and closedown times. Applied Mathematical Modeling, 29: 972–986

    Article  MATH  Google Scholar 

  2. Baba, Y. (1986). On the M[x]/G/1 queue with vacation time. Operations Research Letters, 5: 93–98

    Article  MATH  MathSciNet  Google Scholar 

  3. Choudhury, G. (2002). A batch arrival queue with a vacation time under single vacation policy. Computers and Operations Research, 29: 1941–1955

    Article  MATH  MathSciNet  Google Scholar 

  4. Cox, D.R. (1955). The analysis of non-Markovian stochastic processes by the inclusion of supplementary variables. Proceedings Cambridge Philosophical Society, 51: 433–441

    Article  MATH  Google Scholar 

  5. Doshi, B.T. (1986). Queueing systems with vacations-a survey. Queueing Systems, 1: 29–66

    Article  MATH  MathSciNet  Google Scholar 

  6. Feinberg, E.A. & Kim, D.J. (1996). Bicriterion optimization of an M/G/1 queue with a removable server. Probability in the Engineering and Informational Sciences, 10: 57–73

    Article  MATH  MathSciNet  Google Scholar 

  7. Ke, J.-C. (2001). The control policy of an M[x]/G/1 queueing system with server startup and two vacation types. Mathematical Methods of Operations Research, 54 (3): 471–490

    Article  MATH  MathSciNet  Google Scholar 

  8. Ke, J.-C. & Chu, Y.-K. (2006). A modified vacation model M[x]/G/1 system. Applied Stochastic Models in Business and Industry, 22: 1–16

    Article  MATH  MathSciNet  Google Scholar 

  9. Ke, J.-C. (2007). Operating characteristic analysis on the M[x]/G/1 system with a variant vacation policy and balking. Applied Mathematical Modelling, 31 (7): 1321–1337

    Article  MATH  MathSciNet  Google Scholar 

  10. Kella, O. (1989). The threshold policy in the M/G/1 queue with server vacations. Naval Research Logistics, 36: 111–123

    Article  MATH  MathSciNet  Google Scholar 

  11. Kuo, C.-C., Wang, K.-H. & Lee, S.-L. (2009). Optimal control of the < p, N > -policy M/G/1 queue with server breakdowns and general startup times. International Journal of Information and Management Sciences, 20: 565–577

    MATH  Google Scholar 

  12. Lee, H.W., Lee, S.S., Park, J.O. & Chae, K.C. (1994). Analysis of M[x]/G/1 queue with N policy and multiple vacations. Journal of Applied Probability 31: 476–496

    Article  MATH  MathSciNet  Google Scholar 

  13. Lee, S.S., Lee, H.W. & Chae, K.C. (1995). Batch arrival queue with N policy and single vacation. Computers and Operations Research, 22: 173–189

    Article  MATH  Google Scholar 

  14. Levy, Y. & Yechiali, U. (1975). Utilization of idle time in an M/G/1 queueing system. Management Science, 22: 202–211

    Article  MATH  Google Scholar 

  15. Moreno, P. (2008). Analysis of a Geo/G/1 queuing system with a generalized N-policy and setup-closedown times. Quality Technology & Quantitative Management, 5 (2): 111–128

    Google Scholar 

  16. Tadj, L. & Choudhury, G. (2005). Optimal design and control of queues. TOP, 13 (2): 359–412

    Article  MATH  MathSciNet  Google Scholar 

  17. Takagi, H. (1991). Queueing Analysis: A Foundation of Performance Evaluation. Vol. I, Vacation and Priority Systems, Part I. North-Holland, Amsterdam

    Google Scholar 

  18. Wang, K.-H. & Huang, K.-B. (2009). A maximum entropy approach for the < p, N > -Policy M/G/1 queue with a removable and unreliable server. Applied Mathematical Modelling, 33 (4): 2024–2034

    Article  MathSciNet  Google Scholar 

  19. Zhang, Z.G. & Tian, N. (2001). Discrete time Geo/G/1 queue with multiple adaptive vacations. Queueing Systems, 38: 419–429

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Statistic, National Taichung Institute of Technology, Taichung, 404, Taiwan, China

    Jau-Chuan Ke

  2. Department of Industrial and Engineering Management, National Chiao Tung University, Hsing Chu, 300, Taiwan, China

    Kai-Bin Huang & Wen Lea Pearn

Authors
  1. Jau-Chuan Ke
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kai-Bin Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wen Lea Pearn
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jau-Chuan Ke.

Additional information

Jau-Chuan Ke is a professor of Applied Statistics at National Taichung Institute of Technology, Taiwan. He received his M.S. in Applied Mathematics at National Cheng-Kung University, Taiwan, and his Ph.D. in Applied Mathematics at National Chung-Hsing University, Taiwan. His research interests include stochastic process, queuing theory, reliability, and applied statistics

Kai Bin Huang received the Ph.D. degree in industrial engineering and management from National Chiao-Tung University, Hsinchu, Taiwan, China. He is currently an IT engineer in the Engineering Information System Develop Dept., Ardentec Co. Ltd., Hsinchu. His research interests include Queueing theory, Quality engineering and Applied statistics.

Wen Lea Pearn is a professor of operations research and quality assurance at National Chiao Tung University, Taiwan. He received his PhD degree in operations research from the University of Maryland, College Park, Maryland, USA. He worked at AT&T Bell Laboratories as a quality research scientist before joining National Chiao Tung University. His research interests include process capability, network optimization, production management and queuing theory. His publications have appeared in the Journal of the Royal Statistical Society, Journal of Quality Technology, Journal of Applied Statistics, Statistics, Journal of the Operational Research Society, European Journal of Operations Research, Operations Research Letters, Omega, Networks, International Journal of Production Research, International Journal of Systems Science, Journal of Computational and Applied Mathematics, Quality & Reliability Engineering International, IEEE Transactions on Semiconductor Manufacturing, IEEE Transactions on Electronics Packaging Manufacturing and others.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ke, JC., Huang, KB. & Pearn, W.L. Randomized policy of a poisson input queue with J vacations. J. Syst. Sci. Syst. Eng. 19, 50–71 (2010). https://doi.org/10.1007/s11518-010-5124-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11518-010-5124-z

Keywords

Search

Navigation