1 Introduction

Individual muscle forces change with armload direction. This load direction dependency was used to study muscle coordination in healthy subjects [1, 4, 10, 14, 18] and subjects with shoulder pathologies [5, 20]. The Principal Action (PA), which comprehends load direction dependent electromyography (EMG) parameters [4, 14], is used as a descriptive parameter for muscle coordination. In practice, repeated measurements are performed before and after an intervention, while maximum force around the shoulder may be altered by the intervention, e.g., by pain reduction or muscle tendon transfers [20]. In the comparison of these experiments, we assume that muscle forces scale linearly with external force magnitude. External forces may differ considerably in pre–post measurements [5, 20] and inter-individually [4, 18]. So linearity is a pre-requisite, or should be predictable if muscle contraction patterns are to be compared under these different loading conditions. In the jaw, linear scaling of muscle activity (EMG) and external load was indeed demonstrated [2, 25]. However, non-linear muscle activation scaling with external arm load was reported in the upper extremity [8].

In shoulder inverse dynamic modeling, linearity is generally assumed and incorporated in the load sharing criteria that are needed to mathematically solve the redundancy problem in order to reach a unique muscle activation pattern [3, 7–9, 21]. Praagman et al. [19] introduced a combination of a linear stress and a quadratic energy cost function, which turned out to fit best with non-linear in vivo obtained muscle energy expenditure around the elbow using near infrared spectroscopy. They stated that most cost functions are chosen rather arbitrary, mainly due to the fact that validation is difficult since muscle force cannot be measured accurately in vivo. The EMG based PA method offers an alternative method to compare in vivo observed activation simulated muscle activation, in order to interpret the experimental results and to predict possible load dependencies of shoulder muscle activation patterns in future studies [3, 4].

In the present study, we experimentally test the assumption that relative shoulder muscle forces do not change with armload magnitude. The experiment was numerically simulated, using the Delft Shoulder and Elbow Model (DSEM) with both a linear and an energy related cost function [19, 22–24]. We used the PA, i.e. the direction of maximum muscle activation assessed by either EMG (experiment) or force (simulation), respectively PAexp and PAsim, as a parameter for muscle coordination.

2 Methods

2.1 Subjects

Twelve healthy subjects (five female; three left handed) with a mean age of 26 (SD 2.9 years) took part in the study. The local medical ethical committee granted permission and all subjects gave informed consent.

2.2 Experimental setup

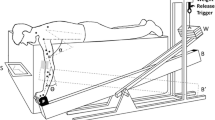
Subjects were seated with the dominant arm in a splint with the elbow in 90° of flexion (Fig. 1). The set-up allowed for static, isometric contractions of shoulder muscles while loading the arm with a force of different magnitudes in different directions in a plane perpendicular to the humerus [3, 4, 18]. The humeral plane of elevation was approximately 60° rotated externally from the para-sagittal plane and the humerus was 60° abducted. The forearm was 45° externally rotated relative to the horizontal plane (see Fig. 1). The objective of the set-up was to record only forces perpendicular to the longitudinal axis of the humerus. In rest, the arm was fully supported by means of a weight and pulley system to compensate for all gravitational forces and moments [4, 18]. The arm splint was attached to a 3D force transducer (AMTI-300, Advanced Mechanical Technology, Inc., Watertown MA, USA) by means of a low friction ball and socket joint. The transducer was mounted on a low friction rail in line with the humerus. This construction allowed for movement of the arm along four degrees of freedom (three rotations and a translation), while translations along the axes perpendicular to the humerus long arm were constrained. These forces controlled the position of a cursor on a computer screen placed in front of the subjects [4, 18] (Fig. 1).

Fig. 1
figure 1

Experimental setup (left panel) and visual feedback (right panel); the subject had the arm in a splint, which was connected to a force transducers. Subjects were required to bring the arm force driven red cursor into the blue target area. The force, perpendicular to the humerus long axis, was recorded with a 6-dof force transducer (AMTI). The target indicated force direction (n = 24) and force magnitude, i.e., radius (n = 6), resulting in 144 combinations

Full size image

EMG activity of 12 shoulder muscles was recorded (Table 1), and off-line post-processed [4, 18]. Nine shoulder muscles were recorded with the use of bipolar silver bar surface electrodes (DelSys, Bagnoli-16, Boston MA, USA, analog filter: 20 Hz high pass, 450 Hz low pass, 10 mm electrode length, inter-electrode distance of 10 mm). Sample rate of analog filtered EMG and force data was 1,000 Hz. Before placement of the electrodes, the skin was abraded, cleaned and a skin preparation gel (Skin Pure, Nihon Kohden) was used. The EMG of the three rotator-cuff muscles was recorded by means of bi-polar wire electrodes (Table 1). The wires were made of Teflon coated stainless steel with bare tips of 2-mm length and were inserted with a sharp hollow needle. The electrode tips were bent in a sharp angle, so that after withdrawal of the needles, the wires would remain in situ. The wires for the m. subscapularis were inserted with a curved needle underneath the medial border of the scapula [12]. Before insertion of the needles, the skin was anaesthetized with a 5% lidocaine solution. The needles for the mm. subscapularis and infraspinatus were inserted until the scapular bone was touched.

Table 1 Experimentally recorded shoulder muscles, localization of the electrodes and type of applied electrodes (similar to [4, 18] for comparison)
Full size table

2.3 Protocol

In the experimental setup, the force task existed of moving a (red) cursor, driven by the forces exerted perpendicular to the longitudinal axis of the upper arm on the force transducer, into a (blue) target area (Fig. 1). Size of the target area was a predetermined area with a range of three times standard deviation (SD), determined from measurements on two subjects. Before the experiment started, the subject’s maximum force target magnitude (F max) that could be maintained in all 24 directions was determined. Subsequently, six force levels were applied equidistantly, covering a range from 17 to 100% of F max. The force driven cursor was to be held within the target area for 2 s, while the target randomly indicated 24 directions (angle) at 6 force magnitudes (radius), resulting in 144 combinations. Between the trials, ample rest of at least 5 s was given in order to avoid too much fatigue effects. Subsequently, the PA at each force magnitude could be determined off-line [4, 18].

2.4 Data post-processing

EMG recordings were full-wave rectified and filtered for visual inspection (3rd order recursive low pass Butterworth at 10 Hz). The 2 s ‘in target’ full-wave rectified EMG was averaged and rest level EMG was subtracted. For each of six force levels, the averaged rectified EMG was normalized with respect to the maximum EMG for the appropriate force level. Subsequently, a parameterized least squares curve was estimated through the 24 EMG values to obtain one direction of maximal EMG activity or Principal Action (PAexp) [4] for every muscle at each force level. Outliers and inaccurate estimations of the PAexp were selected and removed by two investigators when consensus was achieved.

2.5 Statistical analysis

EMG data were collected for n = 12 subjects, n m  = 12 muscles, 24 force directions and n f  = 6 force levels. We tested the H0-hypothesis that muscle coordination did not change under different load magnitudes, i.e., PAexp of each muscle over the six force levels was constant. For each individual muscle a regression line, describing the PA of that muscle as a function of force magnitude, was estimated. Subsequently, the slope coefficient of this line (β) was tested not to differ from zero.

2.6 Model simulations

The experiment was simulated by inverse dynamic numeric modeling using the DSEM [22, 24]. Kinematical input (arm position) was determined using 3D kinematical recording of one subject mounted in the experimental setup using an electromagnetic tracking device [15]. The ISG standardization protocol for the upper extremity including regression based GH-estimation [16, 26] was used. A pointer was used to digitize 14 bony-landmarks with respect to sensors mounted on the thorax, the acromion [13], the upper arm and the forearm. The subjects arm with the sensors attached was positioned into the splint and subsequently the position was recorded. All DSEM simulations were performed using this single position and an external force applied at the elbow in 24 directions at 6 force levels of the model’s F max, exactly simulating the experiment. In order to simulate the weight compensation on the arm in the experiments, gravity working on the humerus in the model was set to zero. By means of inverse dynamic simulation, muscle forces required to satisfy both the mechanical force equilibrium and moment equilibrium were calculated. Two different load sharing criteria were applied: a stress cost function, i.e., minimization of summed squared muscle stresses, and a compound linear and quadratic energy cost function [19]. Based on the estimated muscle forces, the Principal Actions for the muscles in the DSEM were calculated (PAsim) [3, 4].

3 Results

The average maximum force performed within the study population was 65 N (SD = 22.3). PAexp for all muscles and loading conditions, as well as the number of observations after exclusion of outliers, is presented in Table 2. Mm. trapezius pars descendens, deltoideus pars medialis and teres major showed a significant shift of PAexp as a function of external load. The maximum observed effect (m. teres major) of external loading on PAexp was β = −1.08, i.e. −1.08° per % of F max. The PAexp dependency was described by a linear regression model (Table 3).

Table 2 Average Principal Action PAexp (SD) for six relative force levels and n observations
Full size table
Table 3 Linear regression slope parameters for the PAexp to external load and their P values
Full size table

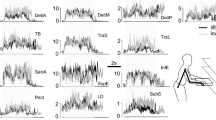
In Fig. 2 changes in PA with respect to PA at the first force level (PA at 17% of F max = 0o) are presented. PAexp are shown (blue circles), together with PAsim, obtained using both a quadratic stress cost function (green upward-pointing triangles) and a compound energy cost function (black downward-pointing triangles). DSEM simulations with a quadratic stress cost function showed very small, but noticeable non-linear scaling. In our model, we simulated gravity compensation of the humerus, but the observed non-linearities could still be introduced by gravity working on the clavicle and scapular bone, which was obviously not controlled for in the in vivo experiments. To make this effect more clearly visible, we performed model simulations including only one force direction, i.e., a force acting downwards on the arm, with two different magnitudes, i.e., 10 and 20 N. We subsequently compared estimated muscle forces in a model with gravity working on the clavicle and scapular bone masses, and a model without. Indeed, we found non-linear external load dependence introduced in the first model in contrast to the simulation with full gravity compensation (Table 4).

Fig. 2
figure 2

Changes in PA with respect to PA at the first force level (PA at 17% of F max = 0o); PAexp (blue circles) and PAsim with bone masses of the scapula and clavicle (stress cost function, green upward-pointing triangles; energy cost function, black downward-pointing triangles). PAexp shows significant non-linear relation to external loading for mm trapezius descendens, deltoideus anterior and teres major. PAsim with the energy cost function and in lesser degree the stress cost function show a non-linear relation with external loading. PAsim of m. deltoideus medialis is lacking because the deltoids in the DSEM are divided in a clavicular part (represented by the m. deltoideus anterior) and a scapular part (represented by the m. deltoid posterior)

Full size image
Table 4 By DSEM simulations estimated muscle forces using the stress cost criteria, without (Fg−) and with (Fg+) taking mass of clavicula (0.156 kg) and scapula (0.705 kg) [22] into account at a vertical downwards directed external load of 10 and 20 N, respectively
Full size table

The compound ‘energy cost function’ appeared to result in a non-linear relation between PAsim and external load. Except for the m. supraspinatus no similarity was observed between PAexp and PAsim (Fig. 2).

4 Discussion

Activation of three shoulder muscles appeared to be load dependent. This has consequences for the interpretation of muscle contraction patterns as measured in patients with shoulder disorders before and after intervention. In shoulder model simulations (DSEM) of the present experiment, non-linearities in the muscle force–external load relationships were not found using a quadratic stress cost function except when gravitational forces working on clavicular and scapular bone mass were incorporated. More pronounced non-linearities were introduced using a compound energy related cost function, however not leading to a better resemblance of PAexp to PAsim.

4.1 Comparison with previous research

Only a few studies assessed load dependency of muscles in vivo. In a previous study by Meskers et al. [17], external load dependency of shoulder muscle activation was found during a similar multi-directional task using a similar EMG processing method. In that study, clockwise shifts of m. deltoideus pars medialis (60°) and counter clockwise shifts of mm. serratus anterior (6°) and m. latissimus dorsi (20°) were found. However, in contrast to the present study: (1) fixed force levels were used without normalizing, meaning that subjects were measured at different percentages of F max; (2) the external loads and force angles were not applied in randomized order, which might introduce muscle activation dependent recruitment bias and fatigue effects at the higher load tasks; (3) the positioning of the subjects in the present study was slightly different, i.e., the elevation angle was 15° lower.

Recruitment of muscles as a function of external load was studied on jaw muscles using a similar technique of relating EMG activity to increasing external forces [2, 22]. With increasing external forces, linear EMG–external force relationships where found for each jaw muscle (part). It was concluded that an increase in activity is achieved by the same, simultaneous increase in excitation activity. This would consequently imply a load independent PA direction. Praagman et al. [19] also reported linear scaling of muscle forces with external loading around the elbow by means of biomechanical model simulation using DSEM and muscle energy expenditure using near infrared spectroscopy. Possible explanations of the discrepancy of the present study with previous work are that with 24 force directions in a full circle around the humerus, the resolution in the present study was considerable higher than in aforementioned studies.

4.2 Clinical consequences

In clinical settings, data are not acquired at different magnitudes of external force but at (near) maximum MVC [5, 20]. Thus, influences of external loading, cross talk and PA estimation accuracy were presumed to be minimal. The maximum force a patient can exert will generally change as a result of therapeutic interventions. In patients it is therefore recommended to acquire PA data at equal percentages of their F max.

The maximum effect of external loading on PA will not exceed 1.08° per percentage of MVC or Newton, resulting in 16° PA shift for an external force change of 15 N for m. teres major. In pre- and post-intervention comparisons, this is in the range of the inter-subject standard deviation and is substantially less than, e.g., observed in patients with massive cuff tears where shifts for m. teres major increased 75° [5, 20]. These large PA changes observed in patients cannot be explained by external force dependency, but are obviously pathology dependent.

4.3 DSEM: load sharing criteria

The applied load-sharing functions either constrain or introduce non-linear scaling. The quadratic stress minimization allows synergy between agonist muscles more than linear criterions [7]. The energy-related cost function with a linear and quadratic component was previously shown to lead to more realistic predictions of muscle activation [19] for elbow–forearm external force tasks. Simulating the present experiment with the compound energy related criterion indeed predicted a non-linear external load-dependent muscle contraction, resulting in a better PAext to PAsim resemblance for the mm. supraspinatus and, at least for the contour also for the m. deltoideus anterior. However, there was no resemblance for the remaining majority of muscles, implying that model simulations do not predict the observed effects in the experiment. In vivo we might apply alternative control strategies that are not caught adequately by the mechanical modeling and load sharing criteria. Additionally, force magnitude and direction induced changes of clavicle and scapula orientation may not be neglected, and should thus experimentally be controlled for, or incorporated in the simulations.

4.4 DSEM: gravitational loads

Introduction of gravitational forces resulted in non-linear muscle force–external load relations when the stress cost function was used, especially for the low loading conditions. Gravitation generates constant joint-torques that requires constant muscle force compensation. This baseline muscle loading interacts with the linear increasing external component, resulting in a non-linear appearance. Where bone masses will not be much of a factor, muscle masses probably will. Muscle masses and the application point of gravitational forces on the different muscle volumes are presently not adequately incorporated in the DSEM. Variations in the gravity forces–external load ratio could explain differences of the present findings with respect to the previous studies to some extent [2, 17, 19, 25]. It is recommended to take gravitational forces into account in model simulations, especially when the direction of the external force does not coincide with the direction of the vertical gravitational forces and the moment arms of external force directions are changing.

4.5 Possible error sources in the present experiment

The validity of the EMG model as used in the present study is extensively discussed [4, 18]. When external force is increased, the signal over noise ratio will increase which will lead to optimal estimates of PAexp. Therefore, PAexp estimations at low forces have reduced accuracy. However, it is unlikely that this phenomenon explains the present findings as shifts of PA are not limited to the lower loading conditions.

Influence of cross talk might also be external load dependent. However, PA is estimated at the peak of muscle activation and therefore the PA method as such can be considered relatively insensitive to cross talk, even at the lower external loads.

During the experiments, the gross position of the subjects was kept constant and special care was taken that subjects could not cheat to be able to meet the higher external forces. Small scapula positional changes could, however, not be ruled out and because external load direction dependent scapular positions were previously observed [6], these changes are likely to increase with increasing external load magnitude influencing muscle moment arms around the SC, AC and GH joints, which affect the PA direction. To what extent PA’s change as a function of scapular position changes requires further research.