Dielectric Properties of Shape-Distributed Ellipsoidal Particle Systems

Abstract

The effective dielectric function of composites consisting of particles dispersed in isotropic or anisotropic media is affected by the composition, size, shape, and orientation of the particles. Our first objective was to determine the effects of the particle’s shape and preferential orientation on the effective dielectric function of the medium. We have used the Maxwell Garnett effective medium approximation generalized for ellipsoidal particles in order to study the effective dielectric function of different Au nanoparticle systems, with both random and normal orientation of the ellipsoids in relation to the incident light, simulating the microstructure of many nanocomposite thin films grown by co-deposition or alternating deposition methods. Our second objective was to consider real particle systems by determining the effects of the particle shape distribution on the effective dielectric function. We have considered the Generalized Maxwell Garnett equations extended for systems of shape-distributed ellipsoids and have, for the first time, correlated the ellipsoid’s shape/aspect ratio with their geometrical factors in a single graphic. We have introduced and used 1D and 2D Gaussian shape probability distribution functions in order to calculate the effective dielectric function of a number of Au nanoparticle systems having different distributions of ellipsoidal shapes/aspect ratios. The multicomponent Generalized Maxwell Garnett approximation was also used in order to determine the effective dielectric function of Au nanoparticle systems containing mixtures of nanoparticles with different shapes and sizes.

Introduction

The dielectric function is one of the most important quantities describing the optical and electrical properties of materials. It is of special interest when studying composite systems. A medium consisting of metallic nanoparticles embedded in another material is an example of an inhomogeneous medium that can be treated by the effective medium approximations (EMAs) or effective medium theories (EMTs). The EMA describes the optical and electrical response of this complex inhomogeneous medium by an average dielectric function that is mostly dependent on the dielectric functions of inclusions and embedding medium and on the volume fraction of the inclusions. Once the dielectric function is known, it becomes easy to access the refractive index and predict all types of optical phenomena, such as reflection or transmission by a thin film of this complex material deposited on a substrate [1, 2].

The most commonly used EMA is the Maxwell Garnett (MG) theory [3], a local-field theory that gives the same result as the Clausius Mossotti formula [4]. It assumes that the inclusions are acting like isolated electric dipoles so that the resulting polarization of the composite material is the sum of the individual microscopic polarizabilities [5]. This approach holds as long as the individual dipoles are independent. If one considers that this condition is fulfilled when one dipole feels only 1% of the electric field created by its neighbors, then the maximum acceptable volume fraction is 0.1 [1]. Another well-known EMA is the Bruggeman approximation, which considers a composite medium made by quasi equivalent mixing of two components [6].

Both MG and Bruggeman models employ the spherical shape concept. However, in real particle systems, the inclusions are usually better described by ellipsoidal shapes and, in addition, the inclusions are usually shape distributed. Generalizations of the MG and Bruggeman equations for ellipsoids of a fixed shape, as well as having distributions of shapes, can be found in literature [2, 7,8,9]. The latter generalizations are based on the distribution functions of geometrical factors¹ of ellipsoids [7], where usually one- or two-dimensional step-like distributions are used over a plane region of geometrical factors capable of including all possible ellipsoidal shapes [2, 7, 9, 10]. However, this procedure lacks accuracy when describing systems of particles with specific distributions of ellipsoidal shapes, since the direct correlation between the particle’s shape/aspect ratio and their geometrical factors has not been performed so far. In this paper, we introduce particle geometries to map exact aspect ratio lines over the geometrical factors’ plane region. From this work, we are able to accurately describe the dielectric function of shape-distributed ellipsoidal particle systems. We demonstrate this by calculating the effective dielectric function of a series of Au nanoparticle (NP) systems of interest to the material-science field using the Generalized Maxwell Garnett (GMG) approximation.

Generalized Maxwell Garnett Approximation with Shape Distribution

We will start by considering a two-component composite in which an assembly of randomly oriented ellipsoidal particles of dielectric constant ε_i and volume fraction f is embedded in an isotropic homogeneous medium of dielectric constant ε_h. Here the subscript i stands for inclusions and h stands for host medium. The inclusions are identical in composition but may be different in shape and orientation and there is no correlation between shape and orientation; all orientations are considered equally probable. The effective dielectric constant of the inhomogeneous medium given by the GMG theory is given by the following expression [7]:

$$ {\varepsilon}_{\mathrm{eff}}=\frac{\left(1-f\right){\varepsilon}_h+ f\beta {\varepsilon}_i}{1-f+ f\beta} $$

(1)

where

$$ \beta =\int \mathrm{P}\left({L}_1\right)\frac{1}{3}\sum \limits_{j=1}^3\frac{\varepsilon_h}{\varepsilon_h+{L}_j\left({\varepsilon}_i-{\varepsilon}_h\right)}d{L}_1 $$

(2)

Or

$$ \beta =\iint \mathrm{P}\left({L}_1,{L}_2\right)\frac{1}{3}\sum \limits_{j=1}^3\frac{\varepsilon_h}{\varepsilon_h+{L}_j\left({\varepsilon}_i-{\varepsilon}_h\right)}d{L}_1d{L}_2 $$

(3)

depending whether we are using a one-dimensional (Ρ(L₁)) or a two-dimensional (Ρ(L₁, L₂)) shape probability distribution function (which will be discussed in the next section). L_j is the jth geometrical factor of the ellipsoid along the j-symmetrical axis, with ∑L_j = 1. The geometrical factors have not got any direct physical meaning, but they are dependent on the shape and can be calculated through the following expression [7]:

$$ {L}_j=\frac{abc}{2}{\int}_0^{\infty}\frac{dq}{\left({z}^2+q\right)\sqrt{\left({a}^2+q\right)\left({b}^2+q\right)\left({c}^2+q\right)}}\genfrac{}{}{0pt}{}{\left(j=1,2,3\right)}{\left(z=a,b,c\right)} $$

(4)

where a, b, and c are the semiaxes of an ellipsoid (see inset of Fig. 2(a) for a visual representation of an ellipsoid with a > b > c) and z takes the value of a, b, or c depending on L_j being L₁, L₂, or L₃, respectively.

If all inclusions have a similar shape and aspect ratio, then Ρ(L₁) or Ρ(L₁, L₂) becomes a delta function at (L₁) or (L₁, L₂) and the β factor simplifies to:

$$ {\beta}^{ellipsoidal\ shape}=\frac{1}{3}\sum \limits_{j=1}^3\frac{\varepsilon_h}{\varepsilon_h+{L}_j\left({\varepsilon}_i-{\varepsilon}_h\right)} $$

(5)

If in addition all inclusions are spherical, then L_j = 1/3 and β further simplifies to:

$$ {\beta}^{spherical\ shape}=\frac{3{\varepsilon}_h}{\varepsilon_i+2{\varepsilon}_h} $$

(6)

which reduces Eq. (1) to the more familiar Maxwell Garnett expression [3]:

$$ {\varepsilon}_{\mathrm{eff}}={\varepsilon}_h+3f{\varepsilon}_h\frac{\varepsilon_i-{\varepsilon}_h}{\varepsilon_i+2{\varepsilon}_h-f\left({\varepsilon}_i-{\varepsilon}_h\right)} $$

(7)

In Eqs. (2–3), we have been considering particles with random orientation. For the special case of ellipsoidal particles oriented with their two major axes (a and b) perpendicular to the incident light, we only consider the two first geometrical factors (L₁ and L₂) in the determination of β:

$$ \beta =\int P\left({L}_1\right)\frac{1}{2}\sum \limits_{j=1}^2\frac{\varepsilon_h}{\varepsilon_h+{L}_j\left({\varepsilon}_i-{\varepsilon}_h\right)}d{L}_1 $$

(8)

Or

$$ \beta =\iint P\left({L}_1,{L}_2\right)\frac{1}{2}\sum \limits_{j=1}^2\frac{\varepsilon_h}{\varepsilon_h+{L}_j\left({\varepsilon}_i-{\varepsilon}_h\right)}d{L}_1d{L}_2 $$

(9)

A particular case of ellipsoids are the spheroids, which have two axes of equal length and therefore have only one independent geometrical factor. Prolate spheroids, for which b = c and L₂ = L₃, can be generated by rotating an ellipse about its major axis. The shape of the prolate ranges from a needle (AR = 0) to a sphere (AR = 1). The following analytical expression for L₁ as a function of the particle aspect ratio (here defined as AR = c/a, considering particles having a > b > c) can be obtained from [7]:

$$ {L}_1=\frac{AR^2}{1-{AR}^2}\left\{\frac{1}{2\sqrt{1-{AR}^2}}\ln \frac{1+\sqrt{1-{AR}^2}}{1-\sqrt{1-{AR}^2}}-1\right\} $$

(10)

whereas

$$ {L}_2={L}_3=\frac{1-{L}_1}{2} $$

(11)

Oblate spheroids, for which a = b and L₁ = L₂, can be generated by rotating an ellipse about its minor axis. The shape of the oblate ranges from a disk (AR = 0) to a sphere (AR = 1). Here we introduce the following analytical expression for L₁ as a function of the particle aspect ratio:

$$ {L}_1={L}_2=\frac{AR\left(\frac{\pi }{2}- ArcSin(AR)- AR\sqrt{1-{AR}^2}\right)}{2{\left(1-{AR}^2\right)}^{3/2}} $$

(12)

whereas

$$ {L}_3=1-2{L}_1 $$

(13)

We will now introduce the concept of “intermediate ellipsoid,” an ellipsoid which has the semiaxis b equal to the average between the semiaxes a and c (i.e., b = (a + c)/2). The importance of this particle shape will become apparent in the next section. It was not possible to solve Eq. (4) analytically for L₁, L₂, and L₃ as a function of AR. However, by using explicit expressions for b and c as a function of a and AR:

$$ b=\frac{a\left(1+ AR\right)}{2} $$

(14)

$$ c= aAR $$

(15)

and by considering a = 1, it was possible to solve Eq. (4) numerically to generate hundreds of data points for each geometrical factor, considering particle’s aspect ratios (ARs) between 0 and 1, and to fit polynomial expressions to each set of data. The intermediate ellipsoid’s L₁, L₂, and L₃ expressions as a function of AR are found in the Appendix section (Eqs. A1–A3).

The plots of the geometric factors given by Eqs. (10–13) and Eqs. (A1–A3) are shown in Fig. 1.

Fig. 1

Geometrical factors: aL₁, bL₂, and cL₃ for prolate/oblate spheroids and for an intermediate ellipsoid as a function of the particle’s aspect ratio

The geometrical factor values of the intermediate ellipsoid are always found between the ones of the prolate and oblate spheroids. However, they only lie close to the average values of the oblate and prolate spheroids for aspect ratios above 0.7. For aspect ratios below 0.7, they are generally closer to the L values of the oblate spheroid shape. The implications of this non-uniform behavior of the ellipsoid’s geometrical factors with AR in the utilization of the shape probability distribution function will be discussed next.

Shape Probability Distribution Function

When considering ellipsoidal particles, either one or two geometrical factors are independent and therefore a region of the L₁L₂ plane can be defined that includes all possible ellipsoidal shapes. For a set of randomly oriented ellipsoidal particles including different shapes and aspect ratios, the geometrical factors L₁ and L₂ are not restricted to a single set of values but are distributed according to some shape probability distribution function Ρ(L₁, L₂). The domain of definition of the shape probability distribution function Ρ(L₁, L₂) lies in one of six possible triangular regions of the L₁L₂ plane, shown in Fig. 2a, each of which corresponds to one of the six possible ways of choosing the relative lengths of the semiaxes a, b, and c of the ellipsoid. In our case, we have decided to work with the a > b > c convention, depicted by the hatched triangular region in Fig. 2a. Spheres, needles, and disks, the three shapes located at each vertex of the triangle, bracket the range of particle possibilities.

Fig. 2

a Domain of definition of the shape probability distribution function Ρ(L₁, L₂). In our case, we have chosen the a > b > c convention, corresponding to the hatched region; b close-up of the hatched region in a, overlapped with the AR lines and with different ellipsoidal particle shape curves. Illustrations of representative particle shapes are drawn to give readers a visual perception of the particle’s geometry through the AR/shape lines

Little work has been done in literature correlating the (L₁, L₂) values in the L₁L₂ plane with the ellipsoid’s AR. The only known method so far is to apply a space transformation from the distribution of geometrical factors into a distribution of aspect ratios [7, 11]. However, the direct mapping of particle shapes was not performed within the shape regions. This work is important so that we can define and use a certain shape probability distribution function Ρ(L₁, L₂) that can accurately represent the mixture of shapes/aspect ratios of a real particle system. In order to graphically correlate the particle’s (L₁, L₂) values with the particle’s ARs, we have determined the positioning of the AR’s major lines in the L₁L₂ plane (given in intervals of 0.1, between 0.1 and 1), as shown in Fig. 2b. Polynomial fittings made to each set of AR data can be found in the Appendix section (Appendix Table 1). Alongside with the already introduced concept of intermediate ellipsoid (in which $a>b=\frac{a+c}{2}>c$), we have introduced two extra particle shape concepts in order to better understand how the different areas in the L₁L₂ plane are correlated with the particle’s shape²: (i) the “intermediate prolate”—an ellipsoidal particle that has the semiaxis b given by the average of the semiaxis c and the semiaxis b of the intermediate ellipsoid (i.e., $a>b=\frac{a+3c}{4}>c$); and (ii) the “intermediate oblate”—an ellipsoidal particle that has the semiaxis b equal to the average of the semiaxis a and the semiaxis b of the intermediate ellipsoid (i.e., $a>b=\frac{3a+c}{4}>c$). Polynomial fittings made to each set of (AR, L₁), (AR, L₂), and (AR, L₃) data points are found in the Appendix section for each particle type (Eqs. A4–A9).

In Fig. 2b, we can observe a slight asymmetry in the spacing between the AR lines: the lower the particle’s aspect ratio is, the greater the spacing between the AR lines over the L₁L₂ region is. Additionally, there is another more pronounced asymmetry in the distribution of shapes lines over the L₁L₂ region: for ARs greater than 0.6–0.7, the particle shape lines are more or less evenly distributed across the AR lines, whereas for ARs lower than 0.6–0.7, the positioning of the intermediate particle’s shape lines over the AR lines becomes increasingly closer to the position of the oblate’s shape line.

Due to the non-uniform correlation between the particle’s shape/aspect ratio and the particle’s geometrical factors in the L₁L₂ plane (Fig. 2b), there is no evidence that the commonly used uniform shape probability distribution function, which is usually positioned in the L₁L₂ region at an equal distance from the prolate and oblate lines [2, 7, 9], will accurately describe a system of ellipsoidal particles with an equal distribution of shapes, as it aims to; e.g., a triangular step-like function centered at an equal distance from the prolate/oblate lines in the middle of the L₁L₂ region will likely have into account a much larger population of particles with shapes closer to the prolate spheroids than to the oblate spheroids. Only if such a distribution is fully positioned in the AR ≥ 0.7 L₁L₂ region could it possibly represent an equal distribution of particle shapes.

Nevertheless, there are different variants of the shape distribution function that make possible to account for the asymmetries found in Fig. 2b. We will consider in this work 1D and 2D Gaussian-type probability distribution functions, or more specifically the normal distribution (Eq. (16)) and the bivariate normal distribution (Eq. (17)), respectively:

$$ G\left({L}_1\right)=\frac{1}{\sqrt{2\pi }\ \sigma }{e}^{-\frac{{\left({L}_1-\mu \right)}^2}{2{\sigma}^2}} $$

(16)

$$ G\left({L}_1,{L}_2\right)=\frac{1}{2\pi \sqrt{1-{\rho}^2}\ {\sigma}_1{\sigma}_2}{e}^{-\frac{\frac{{\left({L}_1-{\mu}_1\right)}^2}{2{\sigma_1}^2}-\frac{\rho \left({L}_1-{\mu}_1\right)\left({L}_2-{\mu}_2\right)}{\sigma_1{\sigma}_2}+\frac{{\left({L}_2-{\mu}_2\right)}^2}{2{\sigma_2}^2}}{1-{\rho}^2}} $$

(17)

where μ and σ are the mean and standard deviation of the distribution function G(L₁) and {μ₁, μ₂}, {σ₁, σ₂}, and ρ are the mean vector, standard deviation vector, and correlation constant of L₁ and L₂ (a real number that varies between −1 < ρ < 1) of the distribution function G(L₁, L₂), respectively. Both 1D and 2D distribution functions should be constrained to the domain of definition shown in Fig. 2, and therefore G is multiplied by the limiting function U, here defined as a product of UnitStep functions:

$$ U\left({L}_1\right)= UnitStep\left({L}_1\right) UnitStep\left(1/3-{L}_1\right) $$

(18)

Or

$$ U\left({L}_1,{L}_2\right)= UnitStep\left({L}_1\right)\ UnitStep\left({L}_2-{L}_1\right)\ UnitStep\left(1-2{L}_2-{L}_1\right) $$

(19)

where

$$ UnitStep(x)=\left\{\begin{array}{c}0\kern1.25em x<0\\ {}1\kern1.25em x\ge 0\end{array}\right. $$

(20)

Since the product G(L₁) U(L₁) or G(L₁, L₂) U(L₁, L₂) can lead to the trimming of the original G function, it should be normalized to unity by further multiplication with the normalization constant K:

$$ {K}_{1\mathrm{D}}=\frac{1}{\int G\left({L}_1\right)U\left({L}_1\right)\ d{L}_1} $$

(21)

Or

$$ {K}_{2\mathrm{D}}=\frac{1}{\iint G\left({L}_1,{L}_2\right)U\left({L}_1,{L}_2\right)\ d{L}_1d{L}_2} $$

(22)

The final expressions for the 1D and 2D Gaussian shape probability distribution functions are then given by:

$$ P\left({L}_1\right)=G\left({L}_1\right)\ U\left({L}_1\right)\ {K}_{1\mathrm{D}} $$

(23)

$$ P\left({L}_1,{L}_2\right)=G\left({L}_1,{L}_2\right)\ U\left({L}_1,{L}_2\right)\ {K}_{2\mathrm{D}} $$

(24)

We use Eq. (23) in Eq. (2), or Eq. (24) in Eq. (3), to determine the β factor, which is needed for computing ε_eff (Eq. (1)). The limits of integration in Eqs. (21–22) and in Eqs. (2–3) are defined according to the domain of definition given in Fig. 2(a)—and in our case, we only need to integrate L₁ between 0 and 1/3 and L₂ between 0 and 1/2.

In the case of single spheroidal particle shapes having a distribution of ARs (i.e., for prolate or oblate particle systems), there is only one independent geometrical factor and therefore the unidimensional shape probability distribution function can be used for determining β (Eq. (2)). This distribution can be used for the intermediate ellipsoid particle shape as well if we solve the L₁ equation (Eq. (A1)) for AR and if we substitute this newly AR = f(L₁) expression in the L₂ equation (Eq. (A2)). By having L₂ = g(L₁) and by using the L₃ = 1 − L₁ − L₂ equality, we can have only one independent geometrical factor as well. In these three cases, we can adjust the two main parameters in the 1D Gaussian probability distribution function (μ and σ) to meet with the description of the particle system. Alternatively, when considering a system of particles with different ellipsoidal shapes and aspect ratios, the bidimensional distribution function can be used for determining the β factor (Eq. (3)). In this case, we can adjust the multiple parameters in the 2D Gaussian probability distribution function (μ₁, μ₂,σ₁, σ₂, and ρ) in order to have it crossing certain AR/shape lines, with the needed asymmetry, to meet with the description of the particle system.

After having correlated the (L₁, L₂) values with the AR of the particles, it is now important to correlate the standard deviation of P(L₁) or P(L₁, L₂) with the one of P(AR). Such correlation can be achieved by the following: (i) segmenting the L₁ and L₂ plots (Fig. 1) into various sections around each major AR value and fitting linear equations to each section (e.g., for 0.95 < AR < 1, we shall have L₁ = m AR + b, for 0.85 < AR < 0.95 we shall have L₁ = m^′AR + b′, and so on); (ii) performing a linear transformation to the random variables (for a probability distribution function of the type P(L₁) = m P(AR) + b, we shall have that ${\mu}_{L_1}=m\ {\mu}_{AR}+b$ and ${\sigma}_{L_1}=m\ {\sigma}_{AR}$); (iii) building large sets of (μ_AR, σ_AR, σ_L) data points and generating the corresponding 3D surface plots. The resulting graphical plots are shown in Fig. 3a and b for the L₁ and L₂, respectively, whereas a more precise set of data correlating (μ_AR, σ_AR) with (μ_L, σ_L) can be found in the Appendix section (Appendix Tables 2, 3, 4, 5, 6, 7, and 8). These values are only needed as an initial input for estimating the parameters in the probability distribution functions. A graphical (visual) adjustment can then take place.

Fig. 3

3D surface plots correlating the standard deviation of the distribution functions aP(L₁) and bP(L₂) with the standard deviation of the distribution function P(AR)

Generalized Maxwell Garnett Approximation for Multicomponent Mixtures

The Generalized Maxwell Garnett approximation in Eq. (1) can be extended for multicomponent mixtures as well [7]:

$$ {\varepsilon}_{\mathrm{eff}}=\frac{\left(1-f\right){\varepsilon}_h+\sum {f}_j{\beta}_j{\varepsilon}_j}{1-f+\sum {f}_j{\beta}_j} $$

(25)

where f_j is the volume fraction of the jth inclusion with dielectric function ε_j, f =  ∑ f_j, and β_j has the same expression as in Eqs. (2–3) with ε_i replaced by ε_j. An advantage of this expression is that it can be used for combining single component mixtures having particle populations with different average sizes and shape distributions.

Simulation Results

In this work, and for the sake of demonstration purposes, we will be considering composite mixtures of Au NP inclusions embedded in a non-absorbing homogeneous host medium having a dielectric function ε_h = 4 (corresponding to a refractive index ${n}_h=\sqrt{\varepsilon_h}=2$). To begin with, the effect of the NP size on the effective dielectric function of a composite will be briefly discussed. Then, the effect of the NP shape on ε_eff will be thoroughly studied, firstly without considering any shape distribution, secondly using 1D shape probability distribution functions and thirdly considering 2D shape probability distribution functions.

Dielectric Function of Au: Size Effects

The dielectric function of the Au NP inclusions ε_i will be calculated using the traditional Drude-Lorentz (DL) model [5]:

(26)

where ω_P is the plasma frequency associated with intraband transitions, with a damping constant γ_P, and z is the number of oscillators necessary to describe the interband part of the dielectric constant, each with resonant frequency ω_j, bandwidth γ_j, and strength f_j. We have used the fitting parameters shown in reference [¹²].

We are going to consider nanoparticles (NPs) small enough so that boundary scattering effects should affect significantly the mean free path l of the conduction electrons. In order to account for these intrinsic size effects, the DL model was modified by correcting the plasmon damping parameter according to the relation [5]:

$$ {\gamma}_{\mathrm{P}}={\upgamma}_0+\frac{A\ {\upsilon}_F}{R} $$

(27)

where γ₀ is the relaxation constant of the bulk metal [12]; A is a phenomenological parameter that is a function of the particle geometry, of the order of unity, and that in practice is adjusted to provide the best fit of the data [13]; υ_F is the Au Fermi velocity (1.39 × 10¹⁵ nm/s); and R is the radius of the nanoparticle (in nm). For the sake of simplicity, we will consider an A = 1 and a particle radius given by the equivalent spherical radius:

$$ {R}_{\mathrm{eq}}=\sqrt[3]{abc} $$

(28)

where a, b, and c are the ellipsoid’s semiaxes.

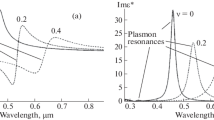
The effects of the NP size on the complex effective dielectric function ε_eff = ε₁ + iε₂ of a composite mixture consisting of spherical Au NPs of different diameters, between 5 and 50 nm, embedded in a non-absorbing homogeneous medium with ε_h = 4 are demonstrated in Fig. 4.

Fig. 4

Complex effective dielectric function of spherical Au NPs embedded in a non-absorbing homogenous host medium with ε_h = 4, calculated using the Generalized Maxwell Garnett theory and the modified Drude-Lorentz model. The NP diameter was varied between 5 and 50 nm. The Au volume fraction was f = 0.01

For spherical NPs smaller than 50 nm, when the size of the homogeneous spherical nanostructures is considerably smaller than the wavelength of the incident light, the displacement of charges within the NP is mostly uniform and the NPs can be described by a dielectric dipole. At the resonance frequency, also called surface plasmon resonance (SPR) frequency, the imaginary parts of both dielectric function and refractive index show a local maximum, meaning that at this frequency the light wave is effectively damped. Spheres absorb strongly in the single narrow band around the frequency where Re(ε_i) =  − 2ε_h. From Fig. 4, we observe that the absorption band intensity increases with the NP size, while the full width at half maximum (FWHM) of the resonance peak decreases with the NP size.

More generally, small NPs of any shape can absorb strongly at frequencies where Re(ε_i) is negative. Ellipsoids will have three absorption bands, and spheroids two, at frequencies determined by the relative lengths of their principal axes. Nevertheless, similar NP size effects are expected for the ellipsoidal NPs. For the sake of simplicity, and during most of the simulation work, we will be considering Au NP inclusions with 5 nm of equivalent spherical radius. Whenever considering particle shape distributions, this can be viewed as the average NP radius of the system of NPs.

Influence of the NP Shape

We will now analyze the influence of the NP shape on the complex effective dielectric function of a composite consisting of randomly oriented Au NPs, with an average diameter of 10 nm, embedded in a non-absorbing homogeneous medium with ε_h = 4. Figure 5a, b, and c depict the calculated real and imaginary parts of the effective dielectric function for the prolate spheroid, oblate spheroid, and intermediate ellipsoid, respectively, using different NP’s aspect ratios.

Fig. 5

Complex effective dielectric function calculated using the GMG theory for different NP shapes: a prolate spheroids, b oblate spheroids, and c intermediate ellipsoids. The NPs were considered to have 10 nm in equivalent spherical diameter and random orientation. For each NP shape, the NP aspect ratio was varied between 0.9 and 0.2 and the ε₁ and ε₂ values were compared to the ones of the spherical NPs (AR = 1). The host medium was considered to be homogeneous and non-absorbing with ε_h = 4. The Au volume fraction was f = 0.01

The SPR is strongly dependent on the NP shape. As it is clearly seen in Fig. 5, for both prolate and oblate spheroids, as the AR decreases, the plasmon resonance splits into a strongly red-shifted long-axis mode (longitudinal plasmon) and a slightly blue-shifted short-axis mode (transverse plasmon). For the intermediate ellipsoid shape, three distinct plasmon resonances appear corresponding to electron oscillations along the three axes of this nanostructure; for high ARs (AR > 0.8), these multiple resonances appear overlapped as one single asymmetric absorption line. As the AR decreases, the long-axes resonances shift to longer wavelengths whereas the short-axis resonance shifts to shorter wavelengths. As the short-axis resonance gets progressively blue-shifted, it partially overlaps with the onset of interband transitions, becoming broader and less intense. Inversely, as the long-axes resonances get progressively red-shifted, they increase in intensity, becoming more prominent.

For the sake of completeness, we have calculated the ε_eff of a similar composite system but now containing Au NPs oriented with their two major axes parallel to the substrate and perpendicular to the incident light (Fig. 6). This simulates the microstructure of many nanocomposites grown by alternating deposition methods [13, 14], whereas the former case (randomly oriented NPs) mimics well the microstructure of nanocomposites grown by co-deposition methods [15, 16].

Fig. 6

Complex effective dielectric function calculated using the GMG theory for different nanoparticle shapes: a prolate spheroids, b oblate spheroids, and c intermediate ellipsoids. The NPs were considered to have 10 nm in equivalent spherical diameter and to be oriented with their two long-axes parallel to the substrate and perpendicular to the incident light. For each NP shape, the NP aspect ratio was varied between 0.9 and 0.2 and the ε₁ and ε₂ plots were compared to the ones of the spherical NP (AR = 1). The host medium was considered to be homogeneous and non-absorbing with ε_h = 4. The Au volume fraction was f = 0.01

When considering ellipsoidal NPs oriented with their two long-axes parallel to the substrate and perpendicular to the incident light, we observe the following: (i) in the prolate spheroids, the same two plasmon resonances that appear in the randomly oriented NPs are present, but with variations in their relative intensities—the red-shifted resonance becomes more intense whereas the blue-shifted resonance becomes less intense. This occurs because now there is only one short-axis resonance contributing to the β factor; (ii) in the oblate spheroids, only the red-shifted resonance is present with increased intensity due to the absence of the short-axis resonance; (iii) in the intermediate ellipsoid, only the two red-shifted resonances appear, with increased intensity, for the same reason as in  the oblate shape case.

Unidimensional Shape Distributions

We have divided the work in this section into the “Single Component Mixtures” subsection, where we compare single Au NP populations of different NP shapes and ARs having similar average NP sizes, and into the “Multiple Component Mixtures” subsection, where we consider mixtures of Au NP populations of different NP shapes and ARs having different average NP sizes as well.

Single Component Mixtures

We will now analyze the influence of the 1D NP shape probability distribution function on the complex effective dielectric function of a composite consisting of randomly oriented Au NPs, with an average diameter of 10 nm, embedded in a non-absorbing homogeneous medium with ε_h = 4. For comparison reasons, two different mean AR values were considered, 0.4 and 0.7, and for each AR the standard deviation σ_AR was varied between 0 and 0.25. Figure 7a, b, and c show the calculated real and imaginary parts of the effective dielectric functions for the prolate spheroid, oblate spheroid, and intermediate ellipsoid, respectively.

Fig. 7

Complex effective dielectric constant calculated using the GMG theory and 1D shape probability distribution functions for randomly oriented: a prolate spheroids, b oblate spheroids, and c intermediate ellipsoids. 1D Gaussian shape probability distribution functions with mean aspect ratios of 0.7 and 0.4 and standard deviations σ_AR ranging from 0.00 to 0.25 were used in the simulations. The host medium was considered to be homogeneous and non-absorbing with ε_h = 4. The Au volume fraction was f = 0.01

Generally, we observe that the greater the aspect ratio’s standard deviation is, the broader and less intense the SPR absorption bands are. This behavior is accentuated for NPs having lower ARs (a case where the longitudinal plasmons are substantially red-shifted away from the threshold for interband absorption). In addition, with the AR’s standard deviation increase, there is a progressive merging of the individual SPR absorption peaks into one single SPR absorption band, which is especially evidenced for NPs with higher ARs (a case where the multiple resonances are positioned closer to each other).

In the prolate spheroid case (Fig. 7a), there is one longitudinal resonance and two transverse resonances, causing an enhancement of the blue-shifted resonance absorption signal. For NPs with higher aspect ratios (AR = 0.7), while increasing the AR’s standard deviation, it is obtained a single asymmetric absorption line—in this case, a pronounced variation in the AR will promote very small changes in the positioning of the transverse modes but large variations in the positioning of the longitudinal mode, causing a smearing of the absorption band(s) in the higher wavelengths. For NPs with lower aspect ratios (AR = 0.4), while increasing the AR’s standard deviation, there is a pronounced smearing of the longitudinal SPR mode, which now remains distinct from the transverse SPR mode, originating a broad absorption line across the visible and near infrared spectra (between 650–1400 nm and beyond the latter limit).

In the oblate spheroid case (Fig. 7b), there are two longitudinal resonances and one transverse resonance, which causes the blue-shifted resonance to appear with low intensity in the absorption spectra. For NPs with higher aspect ratios (AR = 0.7), while increasing the AR’s standard deviation, there is a smearing of the blue-shifted resonance and a merging of the individual absorption peaks into one single absorption band, which progressively becomes broader and red-shifts in position. This red-shift is mainly caused by the nonlinear variation in the SPR peak position with regard to the NP’s AR, i.e., a certain decrement in the NP’s AR will promote a certain red-shift in the SPR peak position that is greater in magnitude than the blue-shift created by a similar increment in the NP’s AR (see Fig. 5b). For NPs with lower aspect ratios (AR = 0.4), the contribution of the transverse resonance is negligible and by increasing σ_AR the single longitudinal SPR red-shifts and becomes broader, promoting a strong absorption across the whole visible and near infrared spectra.

In the intermediate ellipsoid case (Fig. 7b), there are three different SPRs: one long-axis longitudinal resonance, one short-axis transverse resonance, and one intermediate-axis resonance. The three become clear only for lower NP’s ARs. For higher NP’s ARs, they appear merged as one single broad absorption line. In both cases, there is a broadening and a blue-shift of the SPR absorption line with the increase in the AR’s standard deviation, promoting light absorption across the whole visible and near infrared spectra. Again, this is mostly caused by the smearing of the longitudinal SPR absorption peaks at the higher wavelengths.

Multiple Component Mixtures

In this section, we use the GMG formula for multicomponent mixtures (Eq. (25)) in order to evaluate the complex effective dielectric function of a composite system containing mixtures of the following: (i) different groups of Au NPs with similar generic shape, different AR distributions, and different average NP size (Fig. 8a); (ii) different groups of Au NPs with different generic shapes, different AR distributions, and different average NP size (Fig. 8b).

Fig. 8

Complex effective dielectric constant calculated using the GMG theory extended to multicomponent mixtures using different mixtures of Au NP populations between a two prolate spheroid Au NP populations having different average diameters and 1D shape probability distribution functions; b one oblate spheroid Au NP population and one intermediate ellipsoid Au NP population having different average diameters and 1D shape probability distribution functions. The NPs were considered to be randomly oriented within an homogenous non-absorbing medium with ε_h = 4 and the Au volume fraction was f = 0.01

In Fig. 8a, we study the ε_eff of a mixture of two groups of prolate Au NPs having different mean AR and AR’s standard deviation and also different average NP size: group 1 consists of prolate Au NPs with an average NP diameter of 5 nm and with an AR = 0.7 ± 0.10, whereas group 2 consists of prolate Au NPs with an average NP diameter of 15 nm and with an AR = 0.4 ± 0.15. Individually, they show strong absorption bands in different regions of the visible spectra: the 1st group of NPs, represented by the black curve, shows a single broad absorption band located at around 650 nm, whereas the 2nd group of NPs, represented by the yellow curve, shows two clear absorption bands located at around 550 nm and 900 nm. When we consider a mixture of the two groups of NPs using different individual volume fractions in the proportions shown in Fig. 8a (while maintaining the total Au volume fraction constant at f = f₁ + f₂ = 0.01), we obtain absorption lines having mixed characteristics of the two groups of NPs in the proportions given by their individual volume fraction parameters (f₁ and f₂). In this particular example, the mixture of the two Au NP populations resulted in the presence of a wide absorption line across the whole visible-near infrared spectra with enhanced absorption either in the lower wavelengths (mixture with 70% of NPs from the 1st group) or in the higher wavelengths (mixture with 70% of NPs from the 2nd group).

Another example is given in Fig. 8b, where we study the ε_eff of a mixture of two groups of Au NPs having different generic shape, mean AR, AR’s standard deviation, and average NP size: group 1 consists of oblate Au NPs with an average NP diameter of 10 nm and with an AR = 0.8 ± 0.10, whereas group 2 consists of intermediate ellipsoid Au NPs with an average NP diameter of 20 nm and with an AR = 0.5 ± 0.05. One single broad absorption band is obtained for the 1st group of NPs, whereas three distinct absorption peaks are obtained for the 2nd group of NPs. Once again, absorption lines with mixed characteristics of the two main groups of NPs are obtained in the proportions given by their individual volume fraction parameters.

From this demonstration, we can see how versatile the extended GMG method is and how it can aid in the characterization and understanding of the dielectric properties of many complex NP systems.

Bidimensional Shape Distributions

This section is divided into two subsections: the “Single Component Mixtures” subsection, where we study Au NP populations having different NP shapes and ARs (with a similar average NP size), and the “Multiple Component Mixtures” subsection, where we consider mixtures of Au NP populations of different NP shapes, ARs, and sizes. All 3D surface plots and contour plots were generated using Mathematica software.

Single Component Mixtures

We will start by studying how the different 2D shape probability distribution functions P(L₁, L₂) influence the complex effective dielectric function of a composite consisting mostly of Au spherical NPs, with an average diameter of 10 nm, embedded in a non-absorbing homogeneous medium with ε_h = 4. In this case, P(L₁, L₂) will be centered at (1/3, 1/3), corresponding to a NP’s AR = 1, and the AR’s standard deviation (σ_AR) will be varied between 0 and 0.25, encompassing all possible NP shapes. Figure 9a shows the calculated real and imaginary parts of the effective dielectric function, whereas Fig. 9b–d show the 3D surface plots and contour plots of some of the 2D shape probability distribution functions P(L₁, L₂) used in the simulations.

Fig. 9

a Effective dielectric constant calculated using the GMG theory and 2D shape probability distribution functions centered on spherical NPs (AR = 1) with different AR standard deviations σ_AR. 3D surface plots and contour plots are shown for different σ_AR: b 0.05, c 0.15, d 0.25. The NPs were considered to be homogeneously distributed in a non-absorbing medium with ε_h = 4. The Au volume fraction was f = 0.01

Generally, we observe the presence of a single SPR absorption peak centered at around 600 nm, which progressively decreases in intensity, becomes broader, and also blue-shifts with the AR’s standard deviation increase. We can see how this progressive decrease in the SPR peak intensity obtained for standard deviations up to σ_AR = 0.2 can easily be mistaken for a decrease in the NP size (Fig. 4). This behavior can explain discrepancies found in literature when estimating the NP size of nanocomposites containing metal NPs from their optical characterization.

We will now study how a distribution of non-spherical shapes affects the dielectric properties of a nanocomposite system, for a fixed distribution of ARs. Figures 10, 11, and 12 demonstrate how a variation in the NP’s shape standard deviation (σ_shape or σ_s) affects the effective dielectric constant of a nanocomposite system consisting of prolate, oblate, and intermediate ellipsoidal Au nanoparticles, respectively, with an average diameter of 10 nm and a fixed AR = 0.7 ± 0.05, embedded in a non-absorbing homogeneous medium with ε_h = 4. We consider the shape lines “intermediate prolate”, i.p., “intermediate ellipsoid”, i.e., and “intermediate oblate”, i.o., as reference lines for defining how narrow or broad the σ_shape parameter is. The positioning of a certain shape line across the half maximum of the Gaussian peak marks the specific shape standard deviation. The half maximum of the Gaussian peak can be easily accessed through the color bars in the contour plots.

Fig. 10

a Effective dielectric constant calculated using the GMG theory and 2D shape probability distribution functions centered on prolate NPs having AR = 0.7 ± 0.05, with varying shape standard deviations σ_shape. 3D surface plots and contour plots are shown for the different σ_shape: b intermediate prolate (i.p.) line, c intermediate ellipsoid (i.e.) line, d intermediate oblate (i.o.) line. The NPs were considered to be randomly oriented within an homogenous non-absorbing medium with ε_h = 4. The Au volume fraction was f = 0.01

Fig. 11

a Effective dielectric constant calculated using the GMG theory and 2D shape probability distribution functions centered on oblate NPs having AR = 0.7 ± 0.05, with varying shape standard deviations σ_shape. 3D surface plots and contour plots are shown for the different σ_shape: b intermediate oblate (i.o.) line, c intermediate ellipsoid (i.e.) line, d intermediate prolate (i.p.) line. The NPs were considered to be randomly oriented within an homogenous non-absorbing medium with ε_h = 4. The Au volume fraction was f = 0.01

Fig. 12

a Effective dielectric constant calculated using the GMG theory and 2D shape probability distribution functions centered on intermediate ellipsoid NPs having AR = 0.7 ± 0.05, with varying shape standard deviations σ_shape. 3D surface plots and contour plots are shown for the different σ_shape: b intermediate prolate/intermediate oblate (i.p./i.o.) lines, c prolate/oblate (p./o.) lines. The NPs were considered to be randomly oriented within an homogenous non-absorbing medium with ε_h = 4. The Au volume fraction was f = 0.01

A general trend can be observed for both prolate (Fig. 10) and oblate (Fig. 11) particle types. While increasing the shape dispersion along the AR = 0.7 line, the shape of the imaginary part of the effective dielectric constant becomes closer to that of the intermediate ellipsoid. The intermediate ellipsoid’s ε₂ shows one single broad SPR band for this AR (see Fig. 5c), with a line shape between that of the prolate spheroid (Fig. 12a) and that of the oblate spheroid (Fig. 12a). In the prolate case (Fig. 10), the two SP resonances become mingled into one broad absorption peak that increases in intensity with the NP shape dispersion. In the oblate case (Fig. 11), the initial single high intensity SPR band becomes broader and decreases in intensity as we increase the NP shape dispersion. For the intermediate ellipsoid case (Fig. 12), uniformly increasing the NP shape dispersion across the two spheroidal shape regions makes no significant impact on the shape of the ε₂ line. The original intermediate ellipsoid ε₂ line is already close in shape to the averaged ε₂ line of prolates and oblates; thus, an averaging over larger (symmetrical) NP populations of prolates and oblates is not expected to produce a significant variation in the ε₂ line.

We can now study how the distribution of ARs affects the dielectric properties of a nanocomposite system, for a fixed distribution of shapes. We will consider 2D Gaussian shape probability distribution functions P(L₁, L₂) centered on the intermediate ellipsoid shape having a fixed AR with varying standard deviation (AR = 0.4 ± σ_AR), and a fixed NP shape distribution (with the half maximum of the Gaussian peak crossing the intermediate prolate/intermediate oblate lines). We compare these ε_eff to the ones of nanocomposite systems described by 1D Gaussian shape probability distribution functions P(L₁) centered on the same intermediate ellipsoidal shape (AR = 0.4 ± σ_AR). In both cases, we are considering NPs with an average diameter of 10 nm embedded in a non-absorbing homogeneous medium with ε_h = 4. Figure 13 shows the simulated ε₁ and ε₂ curves.

Fig. 13

a Effective dielectric constant calculated using the GMG theory and 2D shape probability distribution functions centered on intermediate ellipsoid NPs (AR = 0.4) with a fixed shape standard deviation (σ_shape is constant at the intermediate prolate/intermediate oblate lines) and with varying AR standard deviations σ_AR. The ${\varepsilon}_{\mathsf{eff}}$ curves of equivalent 1D shape probability distribution functions are also shown. 3D surface plots and contour plots are shown for the different P(L₁, L₂): bσ_AR = 0.05, cσ_AR = 0.10, dσ_AR = 0.15; and for the different P(L₁): eσ_AR = 0.05, fσ_AR = 0.10, gσ_AR = 0.15. The NPs were considered to be randomly oriented within an homogenous non-absorbing medium with ε_h = 4. The Au volume fraction was f = 0.01

The ε₂ curve of the NP system having no shape or AR distribution (i.e., for P(L₁, L₂) = 1 in the specific (L₁, L₂) coordinates) shows clearly three SP resonances across the visible spectrum (centered at around 530 nm, 640 nm, and 770 nm). For the 1D shape probability distribution functions, while increasing σ_AR, the three SPR absorption peaks progressively become broader and decrease in intensity, maintaining their individual shapes until σ_AR = 0.15, a case where the SPR peaks become mingled into one single broad absorption band with its maxima centered at around the second SPR peak position. For the 2D shape probability distribution functions, the SPR peak broadening effect is enhanced for a similar σ_AR, and a single broad absorption band is obtained for σ_AR ≥ 0.10, in this case with its maximum intensity centered at around the third SPR peak position. The first and second SP resonances vanish quickly, at σ_AR ≥ 0.05. For intermediate ellipsoids with low ARs, the 2D Gaussian shape distribution functions have into consideration a slightly larger NP population of oblates than of prolates, which can explain the observed difference in the positioning of the broad SPR peak. Nevertheless, the similarities between the ε₂ curves of the nanocomposites described by 1D and 2D shape probability distributions functions are apparent.

Multicomponent Mixtures

In this section, we use the GMG formula for multicomponent mixtures (Eq. (25)) in order to evaluate the complex effective dielectric function of a composite system containing mixtures of two types of NPs: (i) spherical and close to spherical NPs (AR = 1 ± 0.15, D = 10 nm) and (ii) intermediate ellipsoid NPs (AR = 0.4 ± 0.05, D = 20 nm). Figure 14a shows the calculated ε_eff for different mixtures of NPs. Individually, the two groups of NPs show distinct absorption bands in the visible spectra: the 1st group has a clear single SPR absorption peak at around ~ 600 nm, whereas the 2nd group has three SPR resonances, a main one at ~ 780 nm (high intensity), a secondary one at ~ 650 nm (lower intensity), and a third one at ~ 530 nm (very low intensity). Again, when we consider a mixture of the two groups of NPs, we obtain absorption lines having mixed characteristics of the individual groups in the proportions given by their individual volume fractions.

Fig. 14

a Complex effective dielectric constant calculated through the extended GMG theory using 2D shape probability distribution functions for different mixtures of Au NP populations between (i) spherical-type NPs (AR = 1 ± 0.15, D = 10 nm) and (ii) intermediate ellipsoid-type NPs (AR = 0.4 ± 0.05, D = 20 nm). b 3D surface plots and contour plots of the 70% sphere + 30% intermediate ellipsoid case. In the simulations, the NPs were considered to be randomly oriented within a homogenous non-absorbing medium with ε_h = 4, and the Au volume fraction was f = 0.01

Conclusions

We have correlated, for the first time, the geometrical factors with the relative axis lengths of ellipsoidal particles in the same L₁L₂ plot. Based on this work, different shape probability distribution functions can be used to accurately represent the distribution of shapes of a real ellipsoidal particle system. By choosing an appropriate effective medium approximation, the dielectric function of such a system can then be calculated.

In this paper, we have used the Generalized Maxwell Garnett effective medium approximation for determining the effective dielectric function of composites having embedded ellipsoidal particles with both random orientation and perpendicular orientation to the incident light, simulating the microstructure of many nanocomposites grown by co-deposition and alternating deposition methods, respectively.

We have introduced and used 1D and 2D Gaussian shape probability distribution functions in order to study the effective dielectric function of a number of Au ellipsoidal nanoparticle systems containing different distributions of shapes/aspect ratios. Generally, the greater the aspect ratio’s standard deviation is, the broader and less intense the surface plasmon resonance absorption bands are. This behavior is accentuated for nanoparticles with lower aspect ratios, a case where the longitudinal plasmons are substantially red-shifted away from the threshold for interband absorption. The SPR peak broadening effect is enhanced for 2D shape probability distribution functions. For both prolate and oblate particles of fixed aspect ratio, increasing the shape dispersion in a 2D shape probability distribution function makes the effective dielectric function curves to become closer in shape to the ones of the intermediate ellipsoid particles.

We have used the GMG approximation extended for multicomponent mixtures in order to determine the effective dielectric function of composites containing different populations of nanoparticles in terms of shape and size. Both 1D and 2D shape probability distribution functions were tested resulting in absorption lines with mixed characteristics of the individual nanoparticle populations in the proportions given by their individual volume fractions.

Appendix

In this section, we provide additional equations and tables needed for the calculations shown in this paper.

The nonlinear equations defining the geometrical factors L₁, L₂, and L₃ of the intermediate ellipsoid particles are:

$$ {L}_1=0.6133 AR-0.5520{AR}^2+0.4088{AR}^3-0.1372{AR}^4 $$

(A1)

$$ {L}_2=1.6907 AR-4.2804{AR}^2+6.3189{AR}^3-4.9519{AR}^4+1.5577{AR}^5 $$

(A2)

$$ {L}_3=0.6939-0.5436 AR+0.1831{AR}^2+0.3045{e}^{-5.8532 AR} $$

(A3)

The nonlinear equations defining the geometrical factors L₁, L₂, and L₃ of the intermediate prolate particle are:

$$ {L}_1=0.4536 AR-0.1367{AR}^2+0.013{AR}^3+0.0035{AR}^4 $$

(A4)

$$ {L}_2=3.6484 AR-21.1012{AR}^2+81.5767{AR}^3-206.0110{AR}^4+328.2520{AR}^5-315.8780{AR}^6+167.0350{AR}^7-37.1883{AR}^8 $$

(A5)

$$ {L}_3=0.6769-0.5571 AR+0.2162{AR}^2+0.3171{e}^{-10.0339 AR} $$

(A6)

The nonlinear equations defining the geometrical factors L₁, L₂, and L₃ of the intermediate oblate particle are:

$$ {L}_1=0.7094 AR-0.7515{AR}^2+0.5544{AR}^3-0.1795{AR}^4 $$

(A7)

$$ {L}_2=1.0986 AR-1.9377{AR}^2+2.2904{AR}^3-1.5764{AR}^4+0.4588{AR}^5 $$

(A8)

$$ {L}_3=0.0331-3.2407 AR+0.9161{AR}^2-2.0473{AR}^3+0.9634{e}^{1.5794 AR} $$

(A9)

In all three cases, L₃ can also be calculated from the equality L₃ = 1 − L₁ − L₂.

Table 1 Parameters k₁, k₂, k₃, and k₄ of the polynomial fit performed to each set of AR data points in the L₁L₂ plane shown in Fig. 2b. The general equation has the form L₂ = k₁ + k₂L₁ + k₃L₁² + k₄L₁³

Table 2 Correlation between mean/standard deviation of the AR and of the L₁ for the prolate particle

Table 3 Correlation between mean/standard deviation of the AR and of the L₂ and L₃ for the prolate particle

Table 4 Correlation between mean/standard deviation of the AR and of the L₁ and L₂ for the oblate particle

Table 5 Correlation between mean/standard deviation of the AR and of the L₃ for the oblate particle

Table 6 Correlation between mean/standard deviation of the AR and of the L₁ for the intermediate ellipsoid particle

Table 7 Correlation between mean/standard deviation of the AR and of the L₂ for the intermediate ellipsoid particle

Table 8 Correlation between mean/standard deviation of the AR and of the L₃ for the intermediate ellipsoid particle