Refractive-Index Sensing with Ultrathin Plasmonic Nanotubes

Abstract

We study the refractive-index sensing properties of plasmonic nanotubes with a dielectric core and ultrathin metal shell. The few nanometer thin metal shell is described by both the usual Drude model and the nonlocal hydrodynamic model to investigate the effects of nonlocality. We derive an analytical expression for the extinction cross section and show how sensing of the refractive index of the surrounding medium and the figure of merit are affected by the shape and size of the nanotubes. Comparison with other localized surface plasmon resonance sensors reveals that the nanotube exhibits superior sensitivity and comparable figure of merit.

Appendix

The nonlocal optical properties of the nanotube are determined by solving Maxwell’s wave equation coupled to the hydrodynamic equation for the current [14]. We solve the coupled set of equations by extending the Mie theory for wires of Ref. [25] to core–shell structures. By expanding the electromagnetic fields in the dielectric core, metal shell, and surrounding medium in cylindrical Bessel functions, we can most easily take into account Maxwell’s boundary conditions along with the additional boundary condition of a vanishing normal component of the current in the nonlocal case [14]. Although quantum tunneling is not taken into account with this treatment, we do not expect any such effects to be important in this structure [26, 27].

To determine the extinction property of the infinite cylindrical nanotube we calculate the extinction cross section [28]

$$ \sigma_\text{ext} = -\frac{2}{k_0r_2} \sum\limits_{n=-\infty}^{\infty} {\rm Re}\{a_n\}, $$

(2)

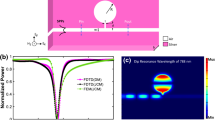
where $k_0=\sqrt{\epsilon_\text{b}} \omega/c$ is the background wave vector, $\epsilon_\text{b}$ is the background permittivity, and a _n is a cylindrical Bessel-function expansion coefficient for the scattered electromagnetic field. We consider a normally incident electric-field polarization perpendicular to the cylinder axis (TM), as sketched in the inset of Fig. 1. The nonlocal-response scattering coefficient is calculated analytically as

$$ a_n=-\frac{\sqrt{\epsilon_\text{b}} J_n(k_0 r_2) \left[C_n + J_n^\prime P_n - H_n^\prime Q_n\right] - \sqrt{\epsilon} J_n^\prime(k_0 r_2) \left[J_n P_n - H_n Q_n\right]} {\sqrt{\epsilon_\text{b}} H_n(k_0 r_2) \left[C_n+ J_n^\prime P_n - H_n^\prime Q_n\right] - \sqrt{\epsilon} H_n^\prime(k_0 r_2) \left[J_n P_n - H_n Q_n\right]}. $$

(3)

Here, J _n and H _n are the Bessel and Hankel functions of the first kind, $k_\text{t} = \sqrt{\epsilon} \omega/c$, and $\epsilon(\omega)=\epsilon_\text{other}(\omega) - \omega_\text{p}^2/(\omega[\omega+i\gamma])$ is the Drude local-response function that includes interband effects through $\epsilon_\text{other}(\omega)$. The arguments of the Bessel and Hankel functions are $k_\text{t} r_2$ unless written explicitly otherwise.

The coefficients P _n , Q _n , and C _n are given by

$$ P_n = p_n \alpha_n + J_n(k_\text{c}r_1) \left[H_n(k_\text{t}r_1) \delta_n + H_n \tau_n \right], $$

(4)

$$ Q_n = q_n \alpha_n + J_n(k_\text{c}r_1) \left[J_n(k_\text{t}r_1) \delta_n + J_n \tau_n \right], $$

(5)

$$ C_n = \frac{i n}{k_0 r_2} \left[ H_n(k_\text{l}r_2) c_n - J_n(k_\text{l}r_2) d_n \right], $$

(6)

where $k_\text{c} = \sqrt{\epsilon_\text{c}} \omega/c$ and $\epsilon_\text{c}$ is the dielectric constant of the core. Furthermore, $k_\text{l}^2=(\omega^2+i\omega\gamma-\omega_\text{p}^2/\epsilon_\text{other})/\beta^2$ and $\beta^2=3 v_\text{F}^2/5$ with $v_\text{F}$ being the Fermi velocity of the metal shell. The coefficients p _n , q _n , α _n , δ _n and τ _n of Eqs. (4–5) are given as

$$ p_n = \sqrt{\epsilon} J_n^\prime(k_\text{c} r_1) H_n(k_\text{t} r_1) - \sqrt{\epsilon_\text{c}} J_n(k_\text{c} r_1) H_n^\prime(k_\text{t} r_1), $$

(7)

$$ q_n = \sqrt{\epsilon} J_n^\prime(k_\text{c} r_1) J_n(k_\text{t} r_1) - \sqrt{\epsilon_\text{c}} J_n(k_\text{c} r_1) J_n^\prime(k_\text{t} r_1). $$

(8)

$$\begin{array}{rll} \alpha_n &=& \left(\frac{k_\text{l} \epsilon_\text{other}}{k_0}\right)^2 \\ &&\times\left[J_n^\prime(k_\text{l}r_2) H_n^\prime(k_\text{l}r_1)-H_n^\prime(k_\text{l}r_2)J_n^\prime(k_\text{l}r_1) \right], \end{array}$$

(9)

$$\begin{array}{rll} \delta_n &=& -\frac{k_\text{l}n^2 \sqrt{\epsilon_\text{c}} \epsilon_\text{other} (\epsilon-\epsilon_\text{other})}{k_\text{t}k_0^2 r_1^2}\\ &&\times\left[ J_n^\prime(k_\text{l}r_2) H_n(k_\text{l}r_1)- H_n^\prime(k_\text{l}r_2) J_n(k_\text{l} r_1) \right], \end{array}$$

(10)

$$\begin{array}{rll} \tau_n &=& -\frac{k_\text{l}n^2 \sqrt{\epsilon_\text{c}} \epsilon_\text{other} (\epsilon-\epsilon_\text{other})}{k_\text{t}k_0^2 r_1 r_2} \\ &&\times\left[ H_n^\prime(k_\text{l}r_1) J_n(k_\text{l}r_1)- J_n^\prime(k_\text{l}r_1) H_n(k_\text{l} r_1) \right], \end{array}$$

(11)

while the coefficients c _n and d _n of Eq. (6) are given as

$$\begin{array}{rll} c_n &=&f_n \left[ J_n^\prime(k_\text{l}r_2) \eta_n + J_n(k_\text{l} r_1) \kappa_n \right]\\ &&+\; J_n^\prime(k_\text{l}r_1) g_n \left[ J_n p_n - H_n q_n \right], \end{array}$$

(12)

$$\begin{array}{rll} d_n &=&f_n \left[ H_n^\prime(k_\text{l}r_2) \eta_n + H_n(k_\text{l} r_1) \kappa_n \right]\\ &&+\; H_n^\prime(k_\text{l}r_1) g_n \left[ J_n p_n - H_n q_n \right], \end{array}$$

(13)

where

$$ g_n = \frac{ink_\text{l} \epsilon_\text{other}(\epsilon-\epsilon_\text{other})}{k_0 k_\text{t} r_2}, $$

(14)

$$ f_n = \frac{in\sqrt{\epsilon_\text{c}} (\epsilon-\epsilon_\text{other})}{k_0 k_\text{t} r_1} J_n(k_\text{t} r_1), $$

(15)

$$ \eta_n = k_\text{l} \left[ J_n(k_\text{t}r_1) H_n^\prime(k_\text{t}r_1) - H_n(k_\text{t} r_1) J_n^\prime(k_\text{t} r_1) \right], $$

(16)

$$ \kappa_n = \frac{n^2 (\epsilon-\epsilon_\text{other})}{k_\text{t} r_2 r_1} \left[ J_n(k_\text{t}r_1) H_n - H_n(k_\text{t}r_1) J_n \right]. $$

(17)

The local-response result can be retrieved in the limit of a vanishing Fermi velocity for which P _n  = p _n , Q _n  = q _n , and C _n  = 0.