1 Introduction

Landslides are among the most pervasive hazards in the world [16, 38, 66]. It is estimated that some 130,000 persons have lost their lives since 1900 because of landslides with economic losses amounting to over USD 50 billion [24, 47].

Slope stability analysis is pivotal to assessing and mitigating the landslide risk. Two main approaches are used by geotechnical engineers to evaluate the stability of slopes, namely the limit equilibrium method (LEM) and the strength reduction method (SRM).

In limit equilibrium methods, the equilibrium of a sliding soil mass is considered. The most popular limit equilibrium technique is the method of slices, in which the soil mass is discretised into vertical slices. Several versions of the method exist based on assumptions regarding the forces between the slices [4,18,32,46,65]. Regardless of the method, a slip surface must be assumed. Non-circular slip surfaces are preferable and recommended by geotechnical standards, especially when dealing with layered soils [17]. The critical slip surface is often determined [20, 51] with various optimisation methods [14,15,16,17,18,19,20,21,,22,44,30,60, 57,63,67, 71]. Although LEMs are widely used thanks to their low computational effort, their main drawback is the validity of the assumed force distributions. For complex scenarios, the strength reduction method is preferred [39].

The SRM is an increasingly popular numerical method to evaluate the factor of safety in geomechanics [24,25,, 23, 68] and is implemented both in the finite element (FEM) and finite-difference method (FDM). Its working principle is to progressively reduce the shear strength of the soil \(\tau _{\rm f}\) as in Equation 1, where \(c'\) and \(\varphi '\) are the cohesion and friction angle, respectively, \(\sigma '\) is the effective normal stress acting on the slip surface, and \({\text{FS}}\) is the factor of safety. FS is increased until failure, defined by unacceptably large deformations or divergence of the calculation.

$$\begin{aligned} \frac{\tau _{\rm f}}{{\rm FS}} =\frac{c' + \sigma '\cdot \tan \varphi '}{{\rm FS}} \end{aligned}$$
(1)

Extensively used in the context of Mohr–Coulomb materials [27,28,29,, 45, 6978], the SRM can be generalised to other nonlinear failure criteria [31,32,, 59, 19]. It enjoys a substantial advantage over the LEM in the generation of realistic stress distributions since it can accommodate complex stress–strain relationships and avoids arbitrary assumptions regarding inter-slice forces [39]. Furthermore, the SRM does not require assumptions on the location and shape of the failure surface, but automatically returns the failure mechanism as an outcome of the calculation. Moreover, unlike the LEM, the SRM can also predict deformations at failure [31]. Finally, the SRM can accommodate both the peak and residual soil strength. However, the computational cost is relatively high compared with LEM.

In this study, we make use of deep learning to reduce the computational effort. As a subset of artificial intelligence (AI), deep learning has been successfully applied in geomechanics and geotechnical engineering, e.g. soil classification, design of deep foundations and tunnels and soil dynamics [35,36,37,38,39,40,41,, 34,58, 64, 70, 72, 76, 74]. Although machine learning has been widely employed in the analysis of slope stability [43,44,45,46,47,48,, 26, 50, 54,55,56, 77], very few attempts [2, 27] have been made on the application of the convolutional neural network (CNN).

CNN is a deep, feed-forward artificial neural network, inspired by the biological visual cortex that has proven to be successful in many different real-life applications, such as image classification, object detection, segmentation, face recognition and self-driving cars. Azmoon et al. [2] framed the slope stability problem as a classification problem by defining eight intervals of the factors of safety computed with the Bishop’s simplified method of slices [4]. By training their CNN on some 95,000 slopes with a constant inclination and homogeneous soil properties, the authors achieved an accuracy of 79% on the test set. He et al. [28] used a CNN to predict the factor of safety of the SRM for two homogeneous and two stratified slopes with variable soil properties of given statistical distribution.

In this study, 600 layered slopes are generated with random profiles, inclined soil layers with random density, cohesion and friction angle and their factor of safety is calculated with the SRM. A CNN is trained on this dataset to predict the factor of safety. Compared to the previous machine learning approaches to the prediction of slope stability, our training dataset considers a wide range of slope profiles, soil layers and properties within a relatively small dataset. Our CNN is capable of predicting the factor of safety with high accuracy, which is also confirmed by cross-checking the results with typical verification examples from the literature [68, 52,53,54,,21, 42, 73].

The novelty of this work lies in the use of CNN to return the factor of safety of slopes of any geometry and stratification, hence bypassing analytical (LEM) or numerical (SRM) methods. Since the factor of safety is instantly predicted by the CNN, the importance of this research lies in the computational gain. As previously mentioned, although both the CNN and SRM are two familiar methods, only few authors succeeded in combining them.

This paper is organised as follows: the data acquisition and augmentation, and the architecture of the CNN are described in Sect. 2. The results of the machine learning prediction are presented in Sect. 3. Finally, the results are discussed (Sect. 4) and conclusions are drawn in Sect. 5.

2 Methods

The general-purpose programming language Python version 3.8.12 [53] is used in this study to generate the random layered slopes and implement the CNN. FLAC3D version 4.00 [31], a three-dimensional explicit Lagrangian finite-difference computer program for engineering mechanics computation, is used to calculate the factor of safety with the SRM.

2.1 Data generation

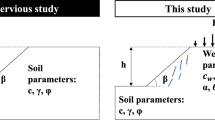
Two-dimensional slopes with the dimension of 100\(\times\)100 m are considered. The left and right boundaries are assigned the coordinates \(x = -20\) m and x = 80 m, respectively (Fig. 1). The bottom and upper boundaries are located at \(y = -\)20 m and y = 80 m. The slope width B is variable between 10 and 60 m and the origin of the coordinates is at the slope toe. The slope angle is randomly chosen every 10 m within the range \(\beta _{\rm s,i} = [5^\circ , 45^\circ ]\). Hence, the slope height is comprised between \(B\tan 5^\circ\) and \(B\tan 45^\circ\), the maximum height being thus \(H = 60\) m. Two plane boundaries between the soil layers are defined by a point with a random x-coordinate, \(y = 0\) and random inclination in the range \(\beta _{\rm p,i} = [-5^\circ , 45^\circ ]\). After each boundary is generated, the whole area below is assigned the soil properties as follows, so that three soil layers are generated. To simulate a broad range of the soil properties, encompassing both drained and undrained conditions, the resulting soil layers are assigned random values of density, cohesion and friction angle between 1100 and 2400 kg/m\(^3\), 0 and 300 kPa, 0 and 45\(^\circ\), respectively. A pseudorandom number generator with constant seed is used to ensure the replicability of the results. The scatter plot of the soil properties is shown in Fig. 2. This figure presents the various combinations of properties of all the soil layers generated. Since the soil properties are randomly chosen, they are approximately uniformly distributed. A uniform distribution of the input features ensures that the CNN is equally trained on the whole spectrum of soil properties. The soil properties are assigned to the soil above a random plane boundary. Since two planes are defined, a maximum of three layers are present. However, if the second plane is completely below the first one, only two soil layers are present. The three soil properties \(\rho\), \(c'\) and \(\varphi '\) are extracted from every element of a 1\(\times\)1 m raster and copied into three 100\(\times\)100 tensors to serve as input for the CNN. These tensors represent the channels \(\rho\), \(c'\) and \(\varphi '\) and are depicted with the heatmaps of Fig. 3. To improve numerical stability [5], the property values are scaled according to Equations 2, where \(\rho _{\rm max}\) = 2400 kg/m\(^3\), \(c'_{\rm max}\) = 300 kPa and \(\varphi '_{\rm max}\) = 45\(^\circ\) are the maximum values of the soil properties considered.

$$\begin{aligned} P= & {} \frac{\rho }{\rho _{\rm max}} \end{aligned}$$
(2a)
$$\begin{aligned} C= & {} \frac{c'}{c'_{\rm max}} \end{aligned}$$
(2b)
$$\begin{aligned} \Phi= & {} \frac{\varphi '}{\varphi '_{\rm max}} \end{aligned}$$
(2c)

FLAC3D input files corresponding to the 3\(\times\)100\(\times\)100 CNN input tensors are generated to calculate the factor of safety with the SRM (Fig. 4). Brick-shaped elements (brick) are used for the bottom and right side of the FLAC3D model and uniform wedge-shaped elements (uwedge) are employed for the slope. The dimension of the mesh elements below the slope is 1\(\times\)1 m. The element width in the slope toe is 1 m and the height is \(\tan (\beta _{\rm {s,i}})\). The number of elements varies between 2080 and 5185, depending on the geometry of the slopes. The displacements are fixed in the horizontal direction at the vertical boundaries, in the direction perpendicular to the analysis plane and in the vertical direction at the bottom. An elastic-perfectly plastic model with Mohr–Coulomb failure criterion is selected with the associated flow rule. The bulk and shear moduli are K = 50 MPa and G = 19 MPa, respectively, and correspond to a Young’s modulus E = 50.8 MPa and Poisson’s ratio \(\nu\) = 0.34. Note that the deformation parameters have a negligible effect on the factor of safety calculated with the SRM [25].

The computed factors of safety of the generated slopes are up to 25. To ensure that the analysis be focused on more practical cases, 34 slopes are neglected for which the factor of safety returned is larger than 10. \(600 - 34 = 566\) slopes are retained.

So far we have elucidated both the input (the tensors with shape 3\(\times\)100\(\times\)100) and output (the vector of the factors of safety calculated with the SRM) of the CNN. Its implementation is described in the next section.

Fig. 1
figure 1

Visual description of the procedure for the generation of the slopes with random soil profile and layers

Full size image
Fig. 2
figure 2

Scatter plot of the dataset of soil properties considered for the layers of the random layered slopes

Full size image
Fig. 3
figure 3

The three channels of the CNN input tensors for the prediction of the factor of safety corresponding to the FLAC3D model

Full size image
Fig. 4
figure 4

Example FLAC3D mesh grid for the computation of the factor of safety with the SRM

Full size image

2.2 Convolutional neural network

Convolutional neural networks are neural networks commonly used for interpreting image data. With the simple architecture of Fig. 5, the “colour” values of the three “image” channels (\(\rho\), \(c'\) and \(\varphi '\)) of Fig. 3 flow through three convolution and subsampling layers, before being flattened and transferred to a fully connected layer that returns the factor of safety. In mathematical terms, convolution layers yield dot products B between the weights of the kernels K (also called “filters”) and subsets of the input tensors A according to Equation 3 where \(n_K\) is the size of the kernels.

$$\begin{aligned} B_{ij} = \sum _{f=0}^{n_{\rm K}-1}\sum _{h=0}^{n_{\rm K}-1}A_{i+h,j+h}K_{i+f,j+h} \end{aligned}$$
(3)

The chosen CNN has 32, 64 and 128 3\(\times\)3 kernels in the first, second and third layer, respectively (Fig. 5). The kernels K slide one cell to the right until the right end of the tensors A is reached, then down and right again. Hence, the dimensions of the tensors shrink by two at each convolution. The output of the convolution layers is delivered to the activation functions to impart nonlinearity to the network.

We select the leaky rectified linear unit (leaky ReLU) activation function [9], defined by Equation 4, with \(z_j = w_{ij}\cdot x_i + b_j\), where \(w_{ij}\) are the weights and \(b_j\) the bias terms of the network.

$$\begin{aligned} a_j :={\left\{ \begin{array}{ll} a_j = \alpha \cdot z_j &{} \text {if } z_j < 0\\ a_j = z_j &{} \text {if } z_j \ge 0 \end{array}\right. } \end{aligned}$$
(4)

The leaky ReLU is derived from the rectified linear unit activation function (ReLU) of equation \(a_j = f(z_j) = \max (0,z_j)\), a common choice for traditional neural networks. ReLU units are affected by the problem of “dying ReLUs”, arising when the activation function constantly returns \(a_j = 0\) [43]. This problem is solved by leaky ReLUs by considering the slope \(\alpha\) for \(z_j \ge 0\) before passing the output to the subsampling layers (Equation 4). The value \(\alpha = 0.1\) is chosen in this study (Fig. 6). The activation function delivers the output to the subsampling layer.

Subsampling helps reduce the dimensions of the tensors to avoid overfitting, which happens when the model fits the training set so well, that it negatively impacts the performance on the test set. The subsampling technique named “max pooling” is considered in this study. To this end, the highest value in a region of the tensor B is selected to return C according to Equation 5 where \(n_{\rm C}\) is the size of the subsampling tensor.

$$\begin{aligned} C_{ij} = \max _{h=0}^{n_{\rm C}-1}B_{i+h,j+h} \end{aligned}$$
(5)

Finally, the output of the last pooling layer is flattened, i.e. the cells of the tensors are inserted one by one into the vector \(d_k = C_{ij}\) that is fed to the fully connected layer to predict the factor of safety.

Notwithstanding the relative simplicity of this CNN architecture, it features already 334,433 training parameters, i.e. the weights \(w_{ij}\) and biases \(b_j\). These parameters are optimised by minimising the mean squared error \({\rm MSE}\) (backpropagation), defined in Equation 6, where \(y_i\) and \({\hat{y}}_i\) are the observed and predicted factors of safety, respectively.

$$\begin{aligned} {\rm MSE} = \sum _{i=1}^n\frac{(y_i-{\hat{y}}_i)^2}{n} \end{aligned}$$
(6)

The \({\rm MSE}\) is minimised using the method for stochastic optimisation Adam [37], with an initial step size (“learning rate”) of 0.001 and the parameters \(\beta _1\) and \(\beta _1\) controlling the decay rate of 0.9 and 0.999, respectively.

Ninety per cent of the data is used to train the CNN and 10% is assigned to validation. This splitting task is performed by the function train_test_split of the Scikit-learn library [48]. Early stopping, an inexpensive way to avoid strong overfitting [3], is implemented by monitoring the CNN performance to ensure that the \({\rm MSE}\) of the validation set decreases of at least 0.001 every 20 steps (patience) and by interrupting the iterations as soon as this criterion is no longer fulfilled.

Since the data generation is rather time-consuming, synthetic data augmentation is employed to increase data availability and, at the same time, improve model performance [49].

Fig. 5
figure 5

Architecture of the CNN used in this study. Image size change and hyperparameters (F: Filter size; N: Number of filters; P: Padding; S: Stride)

Full size image
Fig. 6
figure 6

Comparison between the ReLU and leaky ReLU activation functions of artificial neural networks

Full size image

2.3 Synthetic data augmentation

In the synthetic data augmentation, new training data are generated by performing image transformations, such as reflection, cropping, translation and deformation. The data augmentation is performed after the train/test split to avoid data leakage. In data mining, leakage is the introduction of information about the target that should not be available for mining [35].

Considering that the transformed slopes must yield the same factor of safety of the original ones, two of the above techniques are relevant to our study, namely reflection and translation (Fig. 7). The training dataset size is doubled by simply reflecting the input data X, since the mirrored slopes will yield the same factor of safety of the original slopes. The dataset size is considerably increased by translating upwards the slopes that display constant soil properties at the bottom. Since the maximum height of the slopes is \(H_{\rm max}\) = 60 m and the model top is located at y = 80 m, all slopes can be translated by at least 20 m. The slopes whose crest is below \(y = H_{\rm max}\) can be translated further. To avoid memory issues, the slopes are translated upwards in 2 m steps. Hence, \((100-H_{\rm max})/2 = 20/2 = 10\) translations are considered.

By computing the factor of safety with these input data, the density histogram of the factor of safety shown in Fig. 8 is obtained. Its density histogram is shifted to the left with most data in the interval [0, 5].

Once the data is preprocessed as elucidated in this section, the CNN can be trained as shown in the following.

Fig. 7
figure 7

Synthetic data augmentation transformations applied to the slope images

Full size image
Fig. 8
figure 8

Density histograms of the factors of safety of the training and test sets calculated with the SRM in FLAC3D for the random layered slopes

Full size image

2.4 CNN training and validation

The parameters of the CNN are updated after a mini-batch of training data with a given size has passed through the network. This mini-batch size does not impact the CNN performance, but only its training time [3]. Small mini-batch sizes yield faster computations but require more iterations. There is no general agreement whether a larger mini-batch size should be preferred [66,67,, 10, 61] or vice versa [69,70,, 33, 36]. However, since a larger size determines a faster iteration, we select the largest possible mini-batch allowed by the random access memory of the workstation, namely 4096. The CNN hyperparameters are summarised in Table 1.

Once the training of the CNN is completed, the performance metrics \(R^2\), root mean square error (RMSE) and mean absolute percentage error (MAPE) [75] are computed for the training and validation sets according to Equations 7–9 where \({\bar{y}}\) is the mean factor of safety computed with the SRM and n is the dataset size.

$$\begin{aligned} R^2= & {} 1- \frac{\sum _{i=1}^n(y_i-{\hat{y}}_i)^2}{\sum _{i=1}^n(y_i-{\bar{y}})^2} \end{aligned}$$
(7)
$$\begin{aligned} {\rm RMSE}= & {} \sqrt{\sum _{i=1}^n\frac{(y_i-{\hat{y}}_i)^2}{n}} \end{aligned}$$
(8)
$$\begin{aligned} {\rm MAPE}= & {} \frac{1}{n}\sum _{i=1}^n \left|\frac{y_i-{\hat{y}}_i}{y_i} \right| \end{aligned}$$
(9)

The algorithm workflow is summarised in Fig. 9.

After the calculated factors of safety are predicted with the CNN, the network is further tested on the slope verification examples [68, 52,53,54,, 21, 42, 73, 62] depicted in Fig. 10 and with soil properties according to Table 2.

The results are shown in the next section.

Fig. 9
figure 9

Workflow of the proposed algorithm: input files’ generation, factor of safety computation with the SRM in FLAC3D, CNN training and prediction

Full size image
Fig. 10
figure 10

Slope stability software verification examples considered in this study. Coordinates and numbering of the soil layers

Full size image
Table 1 List of the CNN hyperparameters and their optimised value
Full size table
Table 2 Soil properties of the layers of the slope stability software verification examples considered in this study
Full size table

3 Results

A workstation equipped with an Intel Core i7-4810MQ CPU at 2.80 GHz with 4 cores and 8 logical processors is used for the calculations. The individual factor of safety calculations with the SRM implemented in FLAC3D last on average 30 minutes. Hence, 600 factor of safety calculations are completed in about 12 to 13 days. The training and validation of the CNN require only a matter of a few minutes. Figure 11 shows the decrease of the \({\rm MSE}\) over time for the training and validation of the CNN. The training stops after 70 epochs due to the early stopping callback defined in Sect. 2.2. As expected, the \({\rm MSE}\) on the training set decreases steadily, whereas the \({\rm MSE}\) on the test set decreases and then plateaus. The factors of safety predicted with the CNN against the factors of safety computed with the SRM are shown in Fig. 12 for the training and test sets, where the bisector represents a perfect prediction and the dashed lines ±30% deviations. The prediction is very accurate both on the low and high values of the factor of safety as manifested by the coefficients of determination \(R^2\) of 0.972 and 0.935 on the training and test sets, respectively. Appreciable deviations occur on very few samples. Notice that, due to the data augmentation, certain values of the factor of safety appear more than once in Fig. 12. For instance, if a slope is mirrored or shifted upwards, the input file varies, whereas the factor of safety stays the same. As shown in Table 3, the positive effect of the synthetic data augmentation on the predictive performance is negligible on the training set, but considerable on the test set. The reflection doubles the size of the training set from \(0.9\cdot 566 = 509\) to 1018 and improves the performance on the test set from \(R^2 = 0.929\) to 0.917. The upward translation of the input slopes increases the size of the dataset approximately by a factor of seven from 1018 to 7158 and the coefficient of determination to \(R^2 = 0.935\). Overall, the CNN prediction of the factor of safety matches the SRM computation very well.

In Fig. 13, the factors of safety predicted by the CNN are compared to those computed with the SRM as provided by the verification manuals of the software RS2 [52] and Sofistik [62]. It is evident that the predicted factors of safety approximate the SRM computations very accurately.

Fig. 11
figure 11

Minimisation of the MSE with the CNN for the training and test set after data augmentation

Full size image
Fig. 12
figure 12

CNN predictions compared to the FLAC3D computation of the factor of safety with the SRM

Full size image
Table 3 Effect of the data augmentation on the sample size and performance of the CNN
Full size table
Fig. 13
figure 13

Computed and predicted factors of safety of the verification examples from the literature

Full size image

4 Discussion

We have generated 600 randomly inclined and layered slopes and computed their factors of safety with the SRM in FLAC3D. The information on the geometry and the three soil properties \(\rho\), \(c'\) and \(\varphi '\) of the slopes is filled into 3\(\times\)100\(\times\)100 tensors with which a CNN is trained. The CNN has been trained to predict the factor of safety of the slope with 90% of the data and validated on the remaining 10%. To increase the number of available data points whilst enhancing performance, the input tensors have been reflected and translated upwards. Furthermore, the network has been tested on customary slope stability verification examples.

The results are very accurate and they could be further improved by increasing the original dataset beyond 600 as well as by considering more than two nonlinear boundaries between the soil layers. Some additional features such as pore water pressure, external loads and structures could also be considered. Rather than retraining the CNN from scratch, these features can be included with the transfer learning approach [6, 7], a currently popular technique in deep learning to reuse pre-trained models on new problems. Note, however, that, although the CNN was trained with plane boundaries within the soil layers, it can already predict the factor of safety of more complex boundaries, such as those of the second verification example [21]. A further limitation is the two-dimensional slope analysis that could be circumvented by generating three-dimensional training data and by adapting the model to accommodate three-dimensional convolutions. Finally, more advanced CNN architectures, such as LeNet [41] or AlexNet [40] could be implemented.

5 Conclusions

Despite the aforementioned limitations, our convolutional neural network is considerably accurate both on the training and test set (\(R^2 = 0.935\)) and performs very well on the verification examples. Our method has the potential to assist the slope stability appraisals of the traditional methods. Since the method is trained on the results obtained by the strength reduction, its predictions are more accurate than the limit equilibrium method. The factor of safety is instantly returned by the proposed CNN and the computational effort of the SRM is thus sidestepped.