1 Introduction

Minipiles, or micropiles in general, are often used to increase the capacity of tall towers, offshore foundations and to retrofit existing structures [42]. In addition to the axial loads imposed by the supported superstructures, minipiles are subjected to cyclic lateral loads in the form of wind and wave actions. Coastal structures such as mooring dolphins, berthing structures [34], offshore jacket platforms and pile-supported wharves [70] are often supported by battered piles, which are subjected to cyclic impact loads from ships and waves. The loads imposed by waves on offshore foundations are continuous cycles of forward loading and unloading, followed by reverse loading and unloading [46]. Cyclic lateral loads are usually characterised by the number of cycles, the ratio of maximum to minimum load, the amplitude and the frequency of the loading.

Minipiles are hollow steel piles, very similar to micropiles in physical attributes, except that the former are installed without grouting and hence, have the advantage of easy installation. The design guidelines for micropiles are often used for projecting the practical performance of minipiles, due to the similar characteristics of the two. There is extensive literature on static lateral [45, 48] and static and cyclic compressive and pull-out behaviour of micropiles [17, 29, 59, 57]. However, there is only limited literature on the behaviour of micropiles under cyclic lateral loading. Among the field studies, Abd Elaziz and El Naggar [5] investigated the cyclic behaviour of hollow flexible micropiles in stiff clay, reporting a reduction in stiffness attributed to gap formation between piles and soil due to two-way cyclic loading. A similar observation was made by Fu et al. [30] for piles in soft soil. Brown et al. [15] performed large-scale pile testing on instrumented plugged piles of 273 mm diameter in submerged dense sand under lateral cyclic loading, reporting significant densification of already dense sand with a relatively small loss of resistance due to two-way cyclic loading.

There are several examples in the literature of centrifuge testing of laterally loaded piles subjected to one-way cycling loading in dense sand [39, 50, 68, 72]. The p-y method (proposed by API [10]) has been the state-of-the-art technique for decades for analysing laterally loaded pile foundations [13, 38, 55], and its modification for cyclic loading has also been presented in sand [68, 72] and clay [33, 67]. There are numerous references in the literature to soil resistance being degraded by cyclic loading. The API [10] and DNV [24] recommend using a reduction of soil reaction to account for the accumulation of deformation due to cyclic loading. However, reducing the soil reaction by the stiffness degradation method does not consider the number of load–unload cycles and the load amplitude for the serviceability design conditions [4, 49, 68]. The field observations reported by Long and Vanneste [54] and Li et al. [51] showed that the number of cycles and the pile embedment depth influence the accumulated displacement/rotation, and the recommended p-y curves for cyclic loading were inadequate in predicting long-term behaviour or effect of soil densification. Achmus et al. [7] proposed a ‘degradation stiffness model’, which reduces soil stiffness as a ‘trick’ to account for accumulated deformation, and which also considers the number and amplitude of loading cycles. It was reported by LeBlanc et al. [49] that monopile stiffness increases with cyclic loading in sand, and that the increment is not influenced by relative density (for loose and medium dense sand). There are similar studies suggesting an increase in soil resistance due to local soil densification [23, 51, 68] caused by cyclic loading. While this might seem reasonable for loose sand, as reported by LeBlanc et al. [49] and Abadie et al. [4], interestingly, a similar effect has been observed for dense sand—by Paik [61] in dry sand and by Nicolai and Ibsen [60] and Li et al. [50] in saturated sand. This effect was reported based on the secant stiffness at the pile head, whereas Baek et al. [13] reported, based on cyclic p-y backbone curves, that cyclic loading increases soil resistance in loose sand and decreases soil resistance in dense sand. Numerical modelling of cyclic loading of vertical monopiles has been extensively studied, including by Zhang et al. [74], Allotey and El Naggar [8], Achmus et al. [7] and Kong et al. [46]. These studies indicate that change in stiffness of the soil–pile system is the primary focus of interest when it comes to pile behaviour under cyclic loading.

The above literature only explores the effect of cyclic loading on piles installed vertically, while very limited studies have been dedicated to battered piles [12, 35, 48, 75]. Field testing and application of driven battered pile groups have been reported by Abu-Farsakh et al. [6], as a pier foundation for a twin span bridge built over a lake. Rajashree and Sitharam [66] performed finite element modelling of battered piles in clay and observed soil strength degradation for all cases, among which negatively battered piles (in which the direction of loading is in the direction of the batter) performed the best. It is evident that despite there being extensive literature on the cyclic lateral loading of piles, knowledge of the basic cyclic behaviour of a single battered pile/minipile is lacking. This study aims to close the knowledge gap regarding the effect of repeated loading on the stiffness of soil–pile systems, through 1-g physical modelling of battered minipiles instrumented with optic fibres. The lateral load subjected to battered piles/minipiles is supported by both axial and lateral components, which are responsible for the increased lateral load-carrying capacity of battered minipiles. The axial load acting along the minipile is resisted by skin friction and toe capacity, and the lateral component is supported by the soil pressure perpendicular to the minipile shaft. Thus, the effect of cyclic loading on both the axial and lateral components makes the soil–pile interaction more complex, which is interpreted later in the paper using the multi-surface plasticity macro-model.

2 Testing program

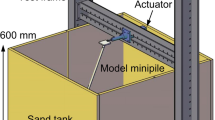
The model minipile tests were performed in a square tank, 1000 mm wide and 600 mm deep. The tank was filled with a locally obtained clean dry silica sand, classified to be poorly graded (d10 = 0.16 mm, d50 = 0.38 mm, dmax = 0.85 mm, Cu = 2.56 and Cc = 1.37) and with maximum (ϒd, max) and minimum (ϒd, min) dry densities of 18.3 and 16.9 kN/m3, respectively [2, 3]. The tank was filled using the pluviation technique, with a sand rainer designed based on Rad and Tumay [65], and a falling height of 400 mm was maintained to achieve a uniform relative density of 90%. Since the influence of batter angles is only prominent in dense sand [75], this relative density was adopted.

2.1 Model minipiles and scaling effect

A primary drawback of 1-g testing is the limited relevance to full-scale minipiles, due to the difference in confining pressure between the model and the field. This can be eliminated considering two scale effects: geometric and stress [9]. The model parameters were geometrically scaled down from a full-scale minipile of diameter 42.4 mm, length 1.6 m and thickness of 2.6 mm. This prototype length was also adopted by Tsang et al. [71] and Guo et al. [37], for minipiles and screw micropiles, respectively. The model minipiles were smooth hollow steel pipes, with an outer diameter of 9.54 mm, thickness of 1.5 mm and length of 360 mm. Since the thickness could not be practically scaled down, the relative stiffness of the model was kept at the same order as for the prototype. The rigidity of the minipile (Krs) based on Eq. (1) (where EpIp is the flexural rigidity of the minipile, Eh is the horizontal soil modulus at the minipile head, and L is the embedded depth of the minipile), proposed by Poulos and Davis [63], was 9.21E-04, so the minipiles could be classified as ‘flexible’.

$$K_{{{\text{rs}}}} = E_{{\text{p}}} I_{{\text{p}}} /E_{{\text{h}}} L^{4}$$
(1)

The ratio of the width of the tank (W) to the pile diameter (B) was always greater than 50, and the ratio of the pile diameter (B) to the representative particle size of the sand, d50, was 25. Hence, there was no (or very negligible) particle size effect based on the criteria suggested by Arshad et al. [11] and Gui and Bolton [36]. Also, the distance from the minipile to the boundary was greater than 18B [69] at all times, to avoid boundary effect.

To scale the stress level, it is common practice to reduce the density of the soil, as sand dilates more at low-stress levels in the model, compared to in the prototype [4, 16, 49]. However, this has not been done for small-scale micropiles [48], likely due to the comparatively shallow embedment depth of the footings. Since the length of the prototype minipile is only 1.6 m in this study, to simulate very dense field conditions, the relative density of the model sand is reduced to only 90%. In 1-g tests, when the soil density in the model matches that of the prototype, the scaling factor for the stress is the same as the factor for the length. Whereas, for strain, it is the square root of the scaling factor, based on the assumption that at small strain, the shear modulus of the soil is proportional to the square root of the confining pressure [41, 40]. It should be noted that this study is intended to phenomenologically discuss the behaviour of various battered minipiles in dense sand and is not corroborated with any field tests. However, to compensate for the disparity in the stress levels, the results will be presented in normalised non-dimensional form, using the following equations for force, displacement and stiffness [4, 51]:

$${\text{normalised lateral force}},\;\;\tilde{H} = \frac{H}{{\gamma^{\prime}L^{2} B}}$$
(2)
$${\text{normalised lateral displacement}},\;\tilde{u} = \frac{u}{B}$$
(3)
$${\text{normalised secant stiffness}},\;\tilde{K} = \frac{{\tilde{K}_{{\text{N}}} }}{{\tilde{K}_{1} }}$$
(4)

where ϒ′, B, KN and K1 are the unit weight of the soil, the diameter of the minipile and the secant stiffness for the Nth and first cycle, respectively. The model minipiles were installed with gentle repeated blows using a hammer, replicating the field installation technique of full-scale steel minipiles using a jackhammer [28]. The effects of other types of installation are not considered in this study, and the results presented here are for driven battered steel minipiles, which might differ for concrete foundations.

2.2 Optic fibre sensing of minipile shaft

Fibre Bragg Grated (FBG) optic fibres were used to measure the strain along the minipile shafts. FBG sensing was chosen due to its high spatial resolution and miniature size, minimising disturbance to the small-sized minipiles. The bare optic fibres were installed on the surfaces of the steel minipiles using cyanoacrylate adhesive. To find the correlation between the shift of wavelength and the measured strain, and to eliminate the possible impact of the stiffness of the adhesive, a calibration process was undertaken. The model minipiles were instrumented with strain gauges and optic fibres, adjacent to each other, and subjected to three-point bending tests. The relationship developed between the strain and the shift of wavelength is:

$$\mu \varepsilon = 281.97\left( {\Delta \lambda } \right) - 0.8932$$
(5)

where με is the recorded microstrain and Δλ is the shift in wavelength from the corresponding FBG. Since quick load tests in sand under controlled laboratory conditions were to be performed, the effect of temperature on wavelength shift was neglected. Each minipile was instrumented with six FBGs, at a spacing of 50 mm, and the optic fibres were placed on the diametrically opposite side of the minipile, as shown in Fig. 1. The ‘positive side’ is the face which is pushed against the soil first, i.e., when the load is applied, it goes into compression first (compression stroke) and then into tension (tension stroke), vice versa for the ‘negative side’.

Fig. 1
figure 1

Loading direction on the minipiles (Hu is the ultimate load)

Full size image

2.3 Test procedure

The testing program consists of three parts: (a) monotonic loading, (b) multi-amplitude two-way symmetrical cyclic lateral loading and (c) long-term single-amplitude two-way symmetrical cyclic lateral loading. The cyclic loads applied in this study are quasi-static with small magnitudes and low frequency. The multi-amplitude loading was adopted to simulate storm type events that induce continuous loading [4]. The frequency was kept constant at 0.1 Hz, similar to in earlier works by Abadie et al. [4] which were based on the findings of Ishihara [43] who concluded that energy dissipation during soil–pile interaction is rate-independent in dry sand. This adopted frequency is similar to the peak frequency of offshore waves and is low enough to avoid dynamic effects. Also, it has been reported that the effect of frequency below 1 Hz is negligible in dry sands [22, 73]. Abd Elaziz and El Naggar [5] applied two-way cyclic lateral loads on flexible hollow micropiles with a load increment of 3 kN and 5 cycles at each loading step. A similar approach has been adopted in this study for the multi-amplitude round. The single-amplitude loading was adopted to highlight the effect of a relatively larger number of cycles at a particular load. The number of cycles adopted in this study was 50, as the change in hysteresis loop area and increase in secant stiffness were mostly noted during the first 50 cycles by Abadie et al. [4]. Hence, the combined outcome of the three parts of the testing program can be used to understand the overall performance of battered minipiles compared to vertical minipiles. For all the conditions, force-controlled load was applied with the aid of an actuator and the displacement was recorded both from the actuator controller system and with laser sensors as shown in the set-up (Fig. 2).

Fig. 2
figure 2

Full test set-up in laboratory

Full size image

Since for minipiles installed vertically in sand, the only force resisting the tensile axial load is skin friction, pull-out tests on vertically installed minipiles were performed to estimate the pile–soil friction angle (δ) [1]. From the force–displacement curve, the ultimate pull-out capacity was estimated to be 15 N. As the skin friction is fully mobilised at the ultimate load, it was considered equivalent to \(\left( {K\overline{\sigma }_{o}^{\prime } \tan \delta } \right)pL\), where K is the lateral earth pressure coefficient, \(\overline{\sigma }_{o}^{\prime }\) is the average effective overburden stress, and p and L are the perimeter and the length of the minipile, respectively [25]. The δ for the model minipiles in very dense conditions was back-calculated to be 0.71φ, which is in the range proposed for full-scale smooth steel piles [47].

3 Results and discussion

3.1 Monotonic loading

The load–displacement curves for monotonic loading at a relative density of 90% were obtained for batter angles of 0°, 25° and 45°. Typically, ‘ + 25°’ denotes a minipile with a batter angle of 25°, where the positive sign indicates that the load is applied in the direction of the batter (and vice versa for a negative sign). The ultimate load capacity can be interpreted from pile load tests corresponding to a particular lateral head displacement [14, 58, 64] or rotation [26, 44]. In this study, the ultimate load (Hu) corresponding to a displacement of 20% of the minipile diameter (B) was adopted based on Broms [14] criteria and is summarised in Table 1.

Table 1 Ultimate load at various batter angles for monotonic loading
Full size table

3.2 Multi-amplitude cyclic loading

3.2.1 Load–displacement curve

The cyclic load is characterised by the loading amplitude, which is the difference between the maximum and minimum loads applied [72]. The loading amplitudes, H, adopted here are 0.2Hu, 0.4Hu, 0.6Hu, 0.8Hu, Hu and 1.2Hu (4 N increments), where Hu is the ultimate lateral load (20 N) of the vertical minipile under monotonic loading. The corresponding normalised loads (\(\tilde{H}\)) using Eq. (2) are 0.18, 0.36, 0.54, 0.71, 0.89 and 1.07. During two-way loading, both the positive and negative batter angles act alternatively, and it is of practical importance to understand how battered minipiles perform overall when subjected to repeated two-way loading. The positive and negative battered minipiles have different ultimate loads, which vary with batter angle. Since the cyclic loading amplitude influences the accumulated deformation [21], Hu was kept constant and equivalent amplitudes were chosen for all cases, so that the hysteresis loops would be comparable. The ultimate load of different minipiles also has an impact on the load cycle, and generally, the amplitudes are also normalised with respect to the lateral bearing capacity [72]. However, only one parameter could be fixed here. As it is general practice to normalise a battered pile’s load capacity with respect to that of the vertical pile [48, 75], similarly, the loading amplitudes for battered minipiles were normalised with respect to the ultimate lateral resistance of the vertical minipile. Thus, the load increment of 4 N was adopted for the vertical and the battered minipiles, to maintain consistency, and at each load increment, the minipile was subjected to 5 cycles with a frequency of 0.1 Hz. The actuator was programmed to apply ramp load, and a typical normalised load versus time input for 0.54 (12 N) is shown in Fig. 3.

Fig. 3
figure 3

Typical normalised load input versus time

Full size image

The hysteresis loops for the three battered angles are shown in Fig. 4, and it can be observed that the loop area increases with the increasing batter angle, which is further discussed later. The accumulated deformations at the minipile head for 0°, 25° and 45° at the end of the multi-amplitude stage of 24 N load amplitude are 0.1, 0.34 and 0 mm, respectively.

Fig. 4
figure 4

Normalised force–displacement curve for multi-amplitude cycling loading for all three batter angles

Full size image

Furthermore, the backbone curves (BBC) were plotted by connecting the force and corresponding displacement for the first and fifth cycles at each loading stage (Fig. 5). The backbone curves are shown for compression and tension strokes, where ‘1st-Comp’ refers to the BBC for the first cycle in compression, ‘5th-Tension’ refers to the BBC for the fifth cycle in tension, and so on. The force–displacement curve for the monotonic loading is plotted for comparison in Fig. 5 for all three batter angles. Figure 5a shows the non-normalised backbone curves for the vertical minipile, and Fig. 5b shows the corresponding normalised plot. (The non-normalised plots for 25° and 45° are omitted for brevity.) In Fig. 5a and b, ‘Vert-90% (Dr)’ refers to the monotonic curve at a relative density of 90%, and similarly, in Fig. 5c, ‘Pos-90% (Dr)’ and ‘Neg-90% (Dr)’ indicate batter angles of + 25° and − 25° at a relative density of 90%.

Fig. 5
figure 5

Backbone curves from the hysteresis loops for three batter angles

Full size image

For the vertical minipile in Fig. 5b, the force–displacement curves indicate greater stiffness in the tension strokes than in the compression strokes, as was also reported by Abd Elaziz and El Naggar [5]. Also in Fig. 5b, the stiffness in the first cycle compression stroke is seen to be similar to the stiffness in the monotonic loading case, until 0.6Hu (0.54), from which point the stiffness in the first cycle compression stroke deteriorates. The first cycle tension stroke curve indicates greater stiffness than the monotonic curve, which becomes steeper after every fifth cycle.

For 25° (Fig. 5c), the slope of the 1st-Comp curve is similar to that of the monotonic curve, until it starts getting steeper (indicating greater stiffness) beyond an applied load of 0.8Hu (0.71). The 5th-Comp curve is the steepest from the beginning, which implies densification due to cyclic loading. The slope of the 1st-Tension curve is initially less steep than the monotonic curve; however, it becomes steeper (indicating greater stiffness) beyond an applied load of 0.6Hu (0.54), following the trend of the 5th-Comp curve. The slope of the 5th-Tension curve is slightly less steep than the slope of the 1st-Tension curve, indicating a very small detrimental effect of cycling. In contrast, for 45° (Fig. 5d), stiffness increases for the tension stroke (5th-Tension) and decreases for the compression stroke (5th-Comp) after five cycles, similar to the vertical case.

The trend of increasing stiffness caused by cyclic loads, seen above, is explained by Brown et al. [15] as being due to the compaction of sand that moves into the gap behind the pile when the pile is pushed forward. During the second half of the cycle, when the load is − Hu, the sand that flowed behind the pile resists the lateral movement of the pile [54]. This can be used to demonstrate why the tension curves indicate higher stiffness than the compression curves. As observed in this study, the two-way cyclic loading improves the pile–soil stiffness in dry dense sand for the 25° battered minipile. However, a similar conclusion cannot be drawn for one-way cycles, as Brown et al. [15] and Cuéllar et al. [23] have suggested that one-way cycles cause less densification than two-way cycles, because more grain subsidence occurs in the latter. It can also be recommended to cycle at smaller loads after installation to increase resistance against ultimate design loads [15] as is evident from this study. The accumulation of contractive volumetric strain observed here in very dense sand is a more common phenomenon for loose cohesionless soil. However, other factors such as load amplitude and number of cycles might influence the evolution of accumulated deformation in sands of other relative densities—requiring further research to be determined.

3.2.2 Secant cyclic lateral stiffness

The secant stiffness variation with the number of cycles and load increment can be analysed using the normalised stiffness, as shown in Fig. 6. The normalised stiffness, \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) (where \(\tilde{K}_{{\text{N}}}\) and \(\tilde{K}_{1}\) are the stiffnesses corresponding to the Nth and first cycle, respectively), reduces to lower than unity at \(\tilde{H}\) of 0.18 (4 N load or 0.2Hu) for all three cases. Then, for the next increment (8 N or 0.4Hu) there is a dramatic increase in stiffness for vertical and 25° battered minipiles. This pattern of increase in \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) continues with each load increment; however, the rate of increase declines gradually at each loading stage. In Fig. 6a, for 0°, after the ultimate load of 20 N, i.e., at 24 N (1.2Hu), the stiffness degrades monotonically and stabilises from the third cycle onwards. For the 25° battered minipile (Fig. 6b), the trend is similar and either the stiffness increases or remains constant approaching the fifth cycle. However, there is no degradation at least until \(\tilde{H}\) of 1.25 (28 N or 1.4Hu), as in the 0° case, because the ultimate load for the positive 25° minipile is 34 N. It should be noted that only the 25° battered minipile was cycled at 28 N (1.4Hu), as positive 25° has the highest load capacity. In contrast, the value of \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) for the 45° minipile is shown in Fig. 6c to never exceed one. However, after the drastic reduction in stiffness with the 4 N loading, the slope gets gradually flatter, approaching unity. Hence, it would be safe to conclude that \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) starts stabilising from after the third cycle for all three batter angles, with only one or two exceptions, and the 25° case performs the best at higher loads.

Fig. 6
figure 6

Normalised stiffness (\(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\)) at the minipile head versus the number of cycles

Full size image

To show the impact of cyclic amplitude on stiffness, the ratio of \(\tilde{K}_{5} /\tilde{K}_{1}\) versus \(\tilde{H}/\tilde{H}_{{\text{u}}}\) is plotted in Fig. 7. At a ratio of 0.4 \(H/H_{{\text{u}}}\), there is an increase in stiffness consistent for all three conditions, which reflects the statement by Brown et al. [15] that cyclic loading at smaller load causes densification. Also, the effect of the first cycle is significant on the pile–soil stiffness, which reduces with an increasing number of cycles [54]. The minipile when first cycled at 0.2Hu causes contractive (positive) volumetric strain, and the soil around the minipile begins to densify slightly. As an effect, when the minipile is next subjected to a cyclic loading amplitude of 0.4Hu, the soil around the minipile contracts even further and a peak value of \(\tilde{K}_{5} /\tilde{K}_{1}\) is observed due to higher positive volumetric strain. This reflects the well-established phenomenon of improving soil characteristics when two-way symmetrical lateral loading is applied to dry dense sand [68], however, only at lower amplitudes. When the soil is now cycled at 0.6Hu, \(\tilde{K}_{5} /\tilde{K}_{1}\) is lower than at 0.4Hu which is due to shearing at higher cyclic amplitude. However, \(\tilde{K}_{5} /\tilde{K}_{1}\) is also more than unity, which indicates some contraction due to repeated loading at 0.6Hu. In the following stages, for the vertical minipile, the normalised stiffness decreases for the consecutive loading amplitudes. For 25° and 45° battered minipiles, it starts increasing from an amplitude of Hu.

Fig. 7
figure 7

Normalised stiffness (\(\tilde{K}_{5} /\tilde{K}_{1}\)) evolution with increasing cyclic load level for three battered angles

Full size image

3.2.3 Interpretation framework

The memory surface elasto-plastic constitutive model for granular soils under cyclic loading is proposed by Corti et al. [20] for triaxial stress conditions. Adopting the same framework for the minipiles, a macro-element modelling approach is presented here for the cyclic behaviour of a 25° battered minipile. Macro-element modelling provides a simplified computational method to calculate the response of a single entity, such as the head force–displacement behaviour of piles [27, 62] and plate anchors [19]. The proposed memory surface hardening model is capable of capturing features such as soil stiffening following cyclic loading and degradation of soil stiffness when subjected to monotonic loading following drained cyclic loading [21]. This framework has an additional memory surface with respect to the existing models [31, 32, 56], which keeps track of previously experienced stress, and it always contains the yield surface.

For two-way cyclic loading on battered minipiles, the slope of the bounding surface in compression stroke (Mbc) is higher than the slope of the bounding surface in tension stroke (Mbt), indicating a higher secant stiffness of minipiles in compression than in tension. The secant stiffness of a minipile, in compression stroke and tension stroke, can be interpreted from the distance between the current loading state and its image on the bounding surface in compression and tension, respectively. The loading state is typically represented in an H-V-M space (where H, V and M are the horizontal force, the vertical force and the moment acting on the minipile head). However, here, the abridged H-V force space is used because the moment for a free-headed pile is zero or constant. For a battered minipile, the applied lateral load can be resolved into two acting forces, the lateral component (H), acting perpendicular to the minipile and resisted by the lateral soil pressure, and the axial load (V), acting along the minipile and supported by the skin friction and toe capacity along the minipile axis. The toe capacity is only considered for negative battered minipiles; however, since the diameter is small for the minipiles, toe capacity is neglected. The positive battered minipile experiences tensile axial load causing positive skin friction (+ V), and the negative battered minipile experiences compressive axial load and negative skin friction (− V).

In Fig. 8a, the load–time plot is presented to show the different phases of the cycle corresponding to the points on the backbone curve for the 25° battered minipile in Fig. 8b. The backbone curve is only shown up to the first two loading amplitudes (for brevity), where the compression and the tension stroke curves are drawn in the positive and negative load quadrants, respectively. The interpretation framework model is shown in Fig. 8c for the 25° minipile head response, where point A is the initial state, which lies within the pre-loading yield and memory surface. As the pile is loaded in compression, it follows the load path A-B and then the minipile is loaded with the same negative amplitude in tension, i.e. B-C (Fig. 8c). When the pile is loaded from A to B, both axial and lateral load components increase, and when the pile is unloaded following B-C, the net change in V (skin friction) is comparatively small due to the summation of positive and negative skin friction. After loading with five cycles at the same amplitude of 0.2Hu in compression stroke, the memory surface expands due to positive plastic volumetric strain, densifying the sand in front of the minipile and increasing the stiffness. In contrast, for the tension stroke, there is a contraction of the memory surface due to dilation of the dense sand behind the minipile, which causes stiffness degradation after five cycles. As a result, new load points are shifted to D and E in compression and tension, respectively (Fig. 8c). The axial load sustained by the skin friction also oscillates between positive and negative values, as the minipile is pushed in compression and tension, respectively. Since B and D are at the same loading amplitude and there is an expansion in memory surface, it would be logical to assume the point D shifts to the left of B. This indicates an accumulation of net negative skin friction as the minipile is pushed from tension to compression. Similarly, when the minipile is unloaded from the direction of positive batter (D-E), there is a net accumulation of positive skin friction and, hence, E is shifted towards the right on the contracted memory surface. In the next stage, at 0.4Hu, the minipile head is sheared to a new higher load and, hence, the memory surface first contracts in compression stroke due to negative volumetric strain. When the minipile is unloaded following F-G, the memory surface expands for the tension stroke within the boundary surface (Fig. 8d). As stated by Gajo and Wood [32] and Corti [21], the stiffness during the unloading path is higher than the normalised stiffness during the initial loading path for larger cyclic amplitudes. The expansion of memory surface to accommodate the contractive volumetric strain in compression stroke is higher than the contraction caused due to the cycles in tension stroke. Thus, the overall stiffness of the minipile–soil system increases as also shown in Fig. 7. This gradual cumulative expansion of memory surface due to the two-way cyclic loading causes it to expand more than during the monotonic loading cases, and hence, the cyclic backbone curves are stiffer. The cyclic loading does not induce enough strength to reach the boundary surface, and hence, no peak in the loading curve is observed.

Fig. 8
figure 8

a Load–time input plot, b backbone curves for 25° minipile, c interpretation framework to demonstrate the effect of repeated loading and d shearing to higher loading amplitude

Full size image

3.2.4 Strain profile and bending moment

For design purposes, it is necessary to understand the strain pattern and its attributes with repeated loading. The strain was measured for the positive and negative sides in compression and tension at the end of every cycle. However, only one side and only fifth cycle data are presented for each batter angle, to provide an insight into the strain profile. Also, to demonstrate the effect of the number of cycles on the strain pattern for each load level, both first and fifth cycle data are plotted in Fig. 9, for 24 N load levels only. In the strain profiles presented, ‘Positive Side’ denotes the face whose optic fibre data are plotted and ‘4 N-5th-C’ denotes strain for a 4 N load at the end of fifth cycle in compression. It should be noted that when the negative side is in compression, it is generally the tension stroke, where the battered pile is pushed on the negative side and vice versa. As shown in Fig. 9a, b, and c (vertical, 25° and 45° batter), when the strains for the fifth and first cycles are compared, there is almost no visible difference in the value, implying no effect of cycling on strain along the minipile. As the steel section is within the elastic limit, the flexural stiffness remains almost constant with changing load amplitudes and number of cycles [54]. However, this might not be the condition for concrete piles [53], requiring further investigation on those types of piles.

Fig. 9
figure 9

Strain profile along minipile shaft with increasing load level for a 0°, b 25° and c 45° (C and T are compression and tension stroke, respectively)

Full size image

The bending moments (M) for the compression and tension strokes were evaluated using Eqs. (6) and (7) and are presented in Fig. 10.

$$\varepsilon_{{\text{t}}} - \varepsilon_{{\text{c}}} = \Delta \varepsilon = \frac{{{\text{MB}}}}{{{\text{EI}}}}$$
(6)
Fig. 10
figure 10

Bending moment along minipile shaft both in compression and tension for various batter angles

Full size image

Or

$$M = \frac{{{\text{EI}}}}{B}\Delta \varepsilon$$
(7)

where εt and εc are the tensile and compressive strains, respectively, B is the pile diameter, E is the modulus of elasticity, and I is the moment of inertia of the minipile section. For 0° (vertical minipile), both the strain (Fig. 9a) and the bending moment (Fig. 10a, b) are smaller for compression than tension strokes, explained by the higher stiffness in the 5th-Tension than the 5th-Comp cycle (Fig. 5a). A similar bending moment pattern is observed for 25° (in Fig. 10c, d), where the moment is higher in tension, even though the 5th-Comp curve has a higher slope than the 5th-Tension curve in Fig. 5c. For the 45° battered minipile (Fig. 10e, f), although the total strain is higher in tension stroke, the bending moment is higher in compression stroke. This behaviour of the 25° and 45° battered minipiles is due to the load decomposition, as a significant part of the load gets converted to axial strain. Of all the three conditions, at any load, the highest bending is recorded for the vertical minipile.

3.3 Long-term single-amplitude loading

3.3.1 Load–displacement curve

To analyse the effect of the number of cycles, in the next round of tests, the minipiles were subjected to 50 two-way cycles at 0.1 Hz frequency. The 0° (vertical) along with the 25° and 45° battered minipiles were subjected to two-way cyclic loading with amplitude of 0.54 (12 N) normalised load, which is 0.6 times the ultimate load (Hu) of the vertical minipile (Fig. 11a). The choice of the ultimate lateral load of the vertical minipile, instead of the respective ultimate load of the battered minipiles, is justified earlier in the multi-amplitude loading section. The vertical minipile was also cycled at its ultimate normalised load of 0.89 (20 N), and the force–displacement curves are shown in Fig. 11b. The hysteresis loop for 0.89 (20 N) is larger than for 0.54 (12 N), as shown in Fig. 11b, and this implies reduced secant stiffness [72]. In Fig. 11c and d, the hysteresis loops for 25° and 45° battered minipiles are shown. As the number of cycles increases, the hysteresis loop shape changes, with a reduction in area implying increased secant stiffness similar to vertically installed minipiles [4]. When looking at the hysteresis loops at the same amplitude, the increased loop area with batter angle is evident (Fig. 11a, c and d). This was also observed by Li et al. [52] and is also visible in Fig. 4. The accumulated deformations for 0°, 25° and 45° at the end of 50 cycles of 12 N load amplitude are 0.02, 0.63 and 0.12 mm, respectively. While the loop area is largest for 45°, indicating overall reduced stiffness, it shows a lower accumulated displacement at the minipile head compared to the 25° battered case.

Fig. 11
figure 11

Normalised force–displacement curve for single-amplitude loading for various batter angles

Full size image

3.3.2 Secant cyclic lateral stiffness

In Fig. 12a, the values of \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) at 0.54 (12 N) and 0.89 (20 N) for the vertical minipile (0°) are compared, indicating that the variation of secant stiffness for 0.54 (12 N) is very small and the minor variation could be due to measurement error. In contrast, for 0.89 (20 N) amplitude, \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) deteriorates with an increasing number of cycles, with a reduction of 2.1–4.5% from the 10th to the 50th cycles (Fig. 12a).

Fig. 12
figure 12

Normalised stiffness (\(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\)) versus number of cycles for single-amplitude loading in a vertical case and b battered cases

Full size image

Figure 12b compares the \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) ratio for 25° and 45° battered minipiles, and it can be observed that the effect of the first cycle is significant for both batter angles. The slope of \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) with an increasing number of cycles is similar for the battered minipiles; however, the hysteresis loop varies in shape (Fig. 11c and d), as explained earlier. After noticeable degradation of stiffness following the first cycle, and more prominently from the 10th cycle, the stiffness starts increasing with the number of cycles. This was also observed by Rosquoet et al. [68]. As the shape of the hysteresis loop gets tighter with the number of cycles, the loop area decreases, and the secant stiffness increases. The rate of change of stiffness gets smaller with an increasing number of cycles for both the battered conditions. Li et al. [50] and Abadie et al. [4] reported the same for vertical piles. While the 45° minipile arrives at a \(\tilde{K}_{{\text{N}}} /\tilde{K}_{1}\) ratio of one, the stiffness of the 25° minipile is marginally more than its first cycle after 50 cycles.

3.3.3 Strain profile

The strain for this loading condition is only presented for one optic fibre (for brevity)—the positive side for 0° at 12 and 20 N amplitude, the negative side for 25° at 12 N (the optic fibre on the positive side was damaged after a few initial cycles) and the positive side for 45° at 12 N, as shown in Fig. 13. The maximum strain for 0° at 12 N in the tension stroke increased slightly with the number of cycles, at a depth of 0.16 m (Fig. 13a). However, in compression stroke, the strain decreased with an increasing number of cycles. For 20 N amplitude (Fig. 13b), the strain in tension remained almost constant. However, in compression, there is a visible rotation point developing around depth 0.31 m after the 10th cycle, which shifts upwards with an increasing number of cycles, at a smaller rate (Fig. 13b).

Fig. 13
figure 13

Strain profile along minipile shaft for all the battered conditions (C and T are compression and tension stroke, respectively)

Full size image

In the case of the 25° battered minipile (Fig. 13c), when the negative side is in compression, the maximum strain decreases with the number of cycles and becomes constant after the 30th cycle, near 0.21 m depth. Similarly, in tension, the rotation point shifts upwards in between 0.26 and 0.31 m depth until the 20th cycle and then stabilises. For 45° (Fig. 13d), the number of cycles seems to have a considerable effect on the measured strain, especially in tension stroke. The maximum negative strain increases significantly until the 20th cycle and then becomes constant, similar to that of the 25° batter angle, and there is no rotation point after the first cycle. This considerable change in strain could be attributed to the lower value of the ultimate load for the negative 45° battered minipile, compared to the vertical minipile. The 12 N amplitude gives a load ratio of 0.5 Hu+45° and 0.8 Hu − 45° with respect to the ultimate lateral loads of the positive and negative 45° battered minipile, respectively.

It should be noted that in single-amplitude cycling, the total strain below the rotation point is very small, so what looks like a rotation point at the outset might be the effective depth of a flexible pile below which there is no strain. This conjecture is further strengthened by the fact that strain at the toe is zero in all cases. As the stiffness increases, the effective depth of the flexible type minipile starts shifting upwards with increasing load cycles.

3.4 Conical depression around a single pile

At the end of the repeated loading, a conical depression was observed (Fig. 14) around the minipile, as was also reported by Cheang and Matlock [18] and Brown et al. [15]. Cuéllar et al. [23] explained that if sand is dense enough, the rearrangement phase starts immediately after the first cycle, which causes the visible subsidence of soil. During this rearrangement, the voids are reduced, and compaction occurs, which supports the hypothesis of densification in already dense sands. Following the densification phase, the soil depression is said to have reached a constant depth and only convective flow of sand particles occurs. The steadying of the secant stiffness after a substantial number of cycles can be attributed to this. It should be noted that the observations of Cuéllar et al. [23] were based on dense saturated sand; however, they predicted it would occur in dry sand as well, possibly to a lower extent. Although the number of cycles in this study is comparatively low and further study is required, the densification phase is well captured for the battered piles, which is of importance.

Fig. 14
figure 14

Conical-shaped depression of sand bed around the 45° minipile

Full size image

4 Conclusion

This 1-g experimental study carried out in very dense sand for flexible type minipiles demonstrates the effect of cyclic lateral loading on battered minipiles. In the multi-amplitude case, vertical (0°) and battered (25° and 45°) minipiles were subjected to five cycles at incremental loading amplitudes, at a low frequency of 0.1 Hz. The backbone curves for the 25° battered minipiles indicate that there was greater stiffness in compression stroke than in tension stroke, and also greater stiffness than in the monotonic loading. The hysteresis loops are visibly different for all the battered cases under multi-amplitude loading, and the largest hysteresis loop was observed for 45°. The normalised stiffness for 0° (vertical) and 25° battered minipiles shows a peak densification effect at 0.4Hu, as an effect of repeated loading at smaller loads. The 45° minipile, however, displayed normalised stiffness values less than unity throughout all the loading amplitudes, which tended to increase for higher cyclic loads. The effect of shearing and cyclic loading with increasing loading amplitude on a 25° battered minipile was interpreted using a multi-surface hardening constitutive model. After every five cycles at each loading stage, the memory surface expanded in compression stroke and contracted in tension stroke, explaining steeper compression backbone curves. There was a very minimal effect of cycling on the strain profile even for battered minipiles during the first five cycles, and the highest bending moment was recorded for 0°.

In the single-amplitude category, a similar trend was observed for the hysteresis loops as in the multi-amplitude category, where the largest hysteresis loop area was for the 45° battered minipile. From the secant stiffness, it was evident that cyclic loading at the ultimate load had a detrimental effect on the vertical minipile. The normalised stiffness for 25° battered minipiles was again the highest tested, reinforcing its better performance capability. However, in both the loading categories, the 45° battered minipile showed very little accumulated deformation at the minipile head, compared to 0° and 25°. Only a very minor effect of repeated loading was observed on the strain profile, except for the 45° battered minipile, which showed some variation initially before stabilising after 30 cycles. The occurrence of conical depression of the sand around the minipile explained the densifying effect in already dense sand and also the phenomenon of stabilising normalised stiffness. Thus, two-way cycling had a prominent densifying effect for a batter angle of 25° than 0° and 45°. Further research is required to determine the effect of one-way loading and first loading direction, to establish whether it is appropriate to assume a stiffness degradation in sand when cycled at loads less than the ultimate load. One of the limitations of this study is that the cyclic load ratio adopted was with respect to the ultimate load of the vertical minipile, as the aim was to apply similar loading amplitudes. The effect of various load ratios with respect to the ultimate load of the respective batter angles (both positive and negative) requires further investigation. Results of this study could be used as a reference for implementing battered minipiles in foundations subjected to repeated two-way lateral loading in very dense or over-consolidated sands with engineering judgement. Furthermore, full-scale testing is required with different pile geometries and soil conditions to testify its general applicability in offshore foundations.