Viscoelastic solutions for stresses and displacements around non-circular tunnels sequentially excavated at great depths

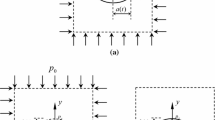
Abstract

This research study presents analytical solutions for the stresses and displacements around deeply buried non-circular tunnels, taking into account the viscoelasticity of the ground, and the sequential excavation of the tunnels’ cross-sections. General initial far-field stress states are assumed, and the time-dependent pressures exerted at the internal tunnel boundaries are found to account for the support effects or water pressures of the hydraulic tunnels. Then, solutions are derived for tunnels with a time-varying sizes and/or shape, by assuming the time-dependent functions specified by the designers. The analytical solutions for the stresses and displacements around elliptical and square tunnels are specifically presented for linearly viscoelastic models using a Muskhelishvili complex variable method and Laplace transform techniques. For validation purposes, numerical analyses are performed for the excavations of elliptical and square tunnels in rock which are simulated by Poynting–Thomson or generalized Kelvin viscoelastic models. Good agreements are observed between the analytical and numerical results of this study. Then, parametric analyses are carried out in order to investigate the effects of the far-field shear stress, along with the distribution forms of the internal pressures, on the ground displacements and stresses. The proposed analytical solutions can be employed to accurately predict the stress concentrations, as well as the time-dependent displacements around deeply buried elliptical or square-shaped tunnels. Furthermore, it is confirmed that this study’s described methodology may be potentially applied to obtain analytical solutions for other arbitrary shaped tunnels sequentially excavated in viscoelastic rock.

Appendix: Method used to determine the inverse mapping function

1.1 Determination of the coefficients in the inverse mapping function

In accordance with the expression of the conformal mapping in Eq. (15), the inverse mapping can be similarly expressed in a Laurent series as [42]:

$$\zeta = \chi (z,t) = A(t)\left[ {z + \sum\limits_{i = 1}^{\infty } {\beta_{i} (t)z^{ - i} } + \beta_{0} (t)} \right]$$

(34)

where A(t) is a positive real function, and β_i(t) (i = 0, 1, …, ∞) are the complex functions. If the region in a z-plane has an axis of symmetry (for example, the x axis in the Cartesian coordinates), then the parameters α_i in Eq. (15) and β_i in Eq. (34) will be real numbers.

Generally speaking, the coefficient A(t) relates with R(t) by the following equation:

$$A(t) = \frac{1}{R(t)}$$

(35)

Due to the fact that a region with an elliptical boundary is not only centro-symmetrical with respect to its origin, but also symmetric on the Ox axis, it can be demonstrated that the coefficients β_i(t) will be real numbers, with i being odd, whereas zero with i being even.

A finite number of items (for example, l items) can be adopted to approximately express the inverse mapping functions. By using the mapping function in Eq. (15), the point z_i in the z-plane will be related with the point ζ_i in the ζ-plane. Then, the corresponding two points, z_i and ζ_i (i = 1, 2, …, q), can be substituted into Eq. (34) in order to provide the set of linear equations with respect to β_k (k = 1, 2, …, l) as follows:

$$\sum\limits_{k = 1}^{l} {\beta_{k} (t)z_{i}^{ - k} } = R(t)\zeta_{i} - z_{i} - \beta_{0} ,\quad i = 1,2, \ldots ,q,$$

(36)

Then, in order to improve the accuracy of the inverse mapping function, the number q of the chosen points can be larger than l (the number of the unknown coefficients in the inverse mapping), which makes Eq. (36) a set of over-determined systems. Then, a least squares method can be adopted to calculate all of the coefficients [38].

1.2 Reliability and accuracy of the inverse mapping function

In the case of the elliptical boundary, if a dimensionless complex variable z₁ is defined as $z_{1} = \frac{z}{c(t)}$, the mapping function in Eq. (15) can be rewritten as:

$$z_{1} = \zeta + \frac{m(t)}{\zeta }$$

(37)

In regard to the square tunnels, z₁ is defined as follows:

$$z_{1} = \frac{z}{R(t)}.$$

(38)

Also, the mapping function, which mapped the boundary of the square tunnel and its exterior in the z₁-plane into the interior of the circle with a unit radius in the ζ-plane, can be expressed as follows [28]:

$$z_{1} = \zeta - \frac{1}{6}\zeta^{ - 3} + \frac{1}{56}\zeta^{ - 7} - \frac{1}{176}\zeta^{ - 11} + \frac{1}{384}\zeta^{ - 15} \cdots$$

(39)

where R(t) is dependent on the square length. For example, if the square length is 5 m, and the first two terms are adopted in Eq. (39), then R can be determined as 2.96 m in order to achieve fewer errors for the majority of the mapped points. Then, by utilizing the method described in Appendix 7.1, where the four negative power terms in the mapping function [Eq. (39)] are employed, the inverse mapping function of the square tunnel can be determined.

In this study, in order to verify the accuracy of the inverse mapping, the curves around the holes on the z₁-plane and ζ-plane determined by the mapping and its inverse are plotted in Fig. 17 for the elliptical and square tunnels. In the figure, the curves in the z₁-plane, which include the mapping of the families of curves with ρ = constant and θ = constant in the ζ-plane (red dashed line), are obtained by Eqs. (37) and (39) [in Eq. (39), only the first two terms in the series are employed]. The curves with a continuous black line on the ζ-plane are obtained by the inverse conformal mapping. By comparing the dashed red lines with the black continuous lines in ζ-plane, it is observed that the curves determined by the inverse mapping are almost consistent with the original curve family (ρ = constant and θ = constant).

Fig. 17

Curves determined by mapping and inverse mapping functions: a, c curves in the z₁-plane determined by mapping function for elliptical and square tunnels, respectively; b, d curves (with black continuous lines) in the ζ-plane determined by inverse mapping function for elliptical and square tunnels, respectively, where the circles and straight lines with dashed red lines are also shown for comparisons

Figures 18 and 19 detail the mapping of the elliptical and square tunnel boundaries in the ζ-plane, respectively, where different numbers of terms in the inverse mapping functions are adopted. Tables 7 and 8 present the coefficients in the inverse mapping of all the cases. Due to the absence of some terms in the mapping function of the square tunnel, the coefficients β_k (k = 1, 5, …) in the inverse mapping of the square tunnel are approximated at zero. Therefore, these coefficients are not presented in Table 8. For the elliptical tunnels (Fig. 18), it is observed that when m is small (for example, m = 0.25 or 0.35), increases in the adopted terms can improve the accuracy of the inverse mapping function. However, the highest accuracy of the case with m = 0.45 (where 12 negative terms are adopted) is still found to be much less than that of the first two cases. In regard to the square tunnels (Fig. 19), it is shown that the accuracy of the inverse mapping function can be slightly improved by increasing the number of terms. Furthermore, it is also observed that the mapped unit circle has greater errors at the corner of the square in all of the cases.

Fig. 18

Mapping of tunnel boundary in the ζ-plane by inverse mapping function with different terms: a1 elliptical boundary with m = 0.25; a2–a4 mappings (with black continuous line) in the ζ-plane when the maximum power of 1/1 z.z in inverse mapping function is 3, 5, 9, respectively; b1 elliptical boundary with m = 0.35; b2–b4 mappings in the ζ-plane when the maximum power of 1/1 z.z in inverse mapping function is 5, 9, 17, respectively; c1 elliptical boundary with m = 0.45; c2–c4 mappings in the ζ-plane when the maximum power of 1/1 z.z in inverse mapping function is 9, 17, 23, respectively

Fig. 19

Mapping of square tunnel boundary: a “squared boundary” determined by conformal mapping; b–d “unit circle” (with black continuous line) in the ζ-plane when the maximum power of 1/1 z.z in inverse mapping function is 7, 15, 31, respectively

Table 7 Coefficients in inverse mapping function for different shaped elliptical tunnels. The absent coefficients are zero

Table 8 Coefficients in inverse mapping function with different number of terms for square tunnels. The absent coefficients are zero