The dilative intake of poroelastic inclusions an alternative to the Mandel–Cryer effect

Abstract

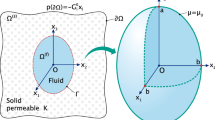
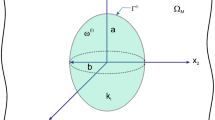
This study examines the time-dependent poromechanics behavior of a fluid-saturated spherical inclusion embedded inside a fluid-saturated porous medium with different poroelastic properties. Both media comprise compressible constituents with distinctively defined poroelastic parameters. It is assumed that the inclusion is subjected to a fluid source at the center. The problem is formulated and solved using Biot theory of poromechanics. The contrasts in inclusion and the medium matrix stiffnesses and their respective hydraulic conductivities can be recognized as two competing factors, which affect the inclusion’s rate of expansion during fluid injection. Findings show a certain type of behavior that the inclusion exhibits at the onset of fluid injection when having greater stiffness than the medium matrix, where the inclusion experiences some decrease in the pore pressure. Compared to what announced as the stress redistribution due the Mandel–Cryer effect in earlier researches on dilation of free spheres, this study shows that the associated phenomenon would be likewise attributed to the coupled nature of pressures and deformations in the theory of poroelasticity. However, it is a consequence of the inclusion-matrix stiffness contrast where a dilating free sphere can be regarded as a special case of this new problem. The asymptotic expansions of pressure terms verify the existence of such an effect. The results of this study would put forward very good insight in some engineering applications.

Appendices

Appendix 1: Arbitrary functions of solution

The arbitrary functions which are found from the solution of Eqs. 21–24 are given below:

$$ A_{1} = {\frac{q}{3s}}\left\{ {{\frac{{ - \psi \omega + \left[ {\psi \omega - \left( {\psi - 1} \right)\theta s} \right]\cosh (\sqrt s ) - \left[ {\psi \omega + \theta s} \right]\sqrt s \sinh (\sqrt s )}}{{\left[ {\psi \omega + \theta s} \right]\sqrt s \cosh (\sqrt s ) + \left[ {\psi \omega + \left( {\psi - 1} \right)\theta s} \right]\sinh (\sqrt s )}}}} \right\} $$

(40)

$$ f_{1} \left( s \right) = {\frac{{q\gamma_{1} \left( {g - 1} \right)\left( {1 - \nu_{1} } \right)\left( {1 - 2\nu_{u1} } \right)}}{s}} \times \left\{ {{\frac{{\left[ {\psi \sqrt s - \sqrt s \cosh \left( {\sqrt s } \right) - \left( {\psi - 1} \right)\sinh \left( {\sqrt s } \right)} \right]}}{{\left[ {\psi \omega + \theta s} \right]\sqrt s \cosh \left( {\sqrt s } \right) + \left[ {\psi \omega + \left( {\psi - 1} \right)\theta s} \right]\sinh \sqrt s }}}} \right\} $$

(41)

$$ A_{2} = {\frac{{q\gamma_{1}^{2} \left( {1 - \nu_{1} } \right)\left( {1 - \nu_{u1} } \right)\left( {\nu_{u2} - \nu_{2} } \right){\text{e}}^{{\left( {{\frac{\psi }{\lambda }} - 1} \right)}} }}{{3\gamma_{2}^{2} gs\left( {1 - \nu_{2} } \right)\left( {1 - \nu_{u2} } \right)\left( {\nu_{u1} - \nu_{1} } \right)}}} \times \left\{ {{\frac{{\theta s^{{{\frac{3}{2}}}} - \omega \left[ {\sqrt s \cosh \left( {\sqrt s } \right) - \sinh \left( {\sqrt s } \right)} \right]}}{{\left[ {\psi \omega + \theta s} \right]\sqrt s \cosh \left( {\sqrt s } \right) + \left[ {\psi \omega + \left( {\psi - 1} \right)\theta s} \right]\sinh \sqrt s }}}} \right\} $$

(42)

$$ B_{2} = - {\frac{{q\gamma_{1} \left( {1 - \nu_{1} } \right)\left( {1 - \nu_{u1} } \right)}}{{3s^{2} \gamma_{2} \left( {1 - \nu_{2} } \right)\left( {1 - \nu_{u2} } \right)\left( {\nu_{u1} - \nu_{1} } \right)}}} \times \left\{ {{\frac{{\psi s^{{{\frac{3}{2}}}} \left[ {\gamma_{1} \left( {\nu_{u2} - \nu_{2} } \right)\theta + \chi } \right]}}{{\left[ {\psi \omega + \theta s} \right]\sqrt s \cosh \left( {\sqrt s } \right) + \left[ {\psi \omega + \left( {\psi - 1} \right)\theta s} \right]\sinh \sqrt s }}}} \right. + \left. {{\frac{{ - \left[ {\gamma_{1} \left( {\nu_{u2} - \nu_{2} } \right)\psi \omega + \psi s} \right]\sqrt s \cosh \left( {\sqrt s } \right) + \left[ {\gamma_{1} \left( {\nu_{u2} - \nu_{2} } \right)\psi \omega - \chi \left( {\psi - 1} \right)s} \right]\sinh \left( {\sqrt s } \right)}}{{\left[ {\psi \omega + \theta s} \right]\sqrt s \cosh \left( {\sqrt s } \right) + \left[ {\psi \omega + \left( {\psi - 1} \right)\theta s} \right]\sinh \sqrt s }}}} \right\} $$

(43)

where the constants ψ, θ, ω and χ are defined as:

$$ \psi = \lambda \left( {\sqrt {{\frac{s}{\xi }}} + 1} \right) $$

(44)

$$ \theta = \left( {1 - \nu_{1} } \right)\left[ {1 + \nu_{u1} + 2g\left( {1 - 2\nu_{u1} } \right)} \right] $$

(45)

$$ \omega = 6\left( {g - 1} \right)\left( {\nu_{u1} - \nu_{1} } \right) $$

(46)

$$ \chi = 3\gamma _{2} (1 - \nu _{2} )(1 - \nu _{{u2}} )(\nu _{{u1}} - \nu _{1} ) $$

(47)

Appendix 2: Special case solution for fluid injection at the center of a poroelastic inclusion inside an elastic matrix

Here, we consider the case involving no pore fluid in the matrix but within the inclusion. The ordinary boundary value equation for fluid content increment in Laplace domain can be written as follows:

$$ \tilde{\zeta^{\prime\prime}}_{1} \left( {r,s} \right) + {\frac{2}{r}}\tilde{\zeta^{\prime}}_{1} \left( {r,s} \right) - s\tilde{\zeta }_{1} \left( {r,s} \right) = 0 $$

(48)

$$ \tilde{\zeta }^{\prime}_{1} \left( {1,s} \right) = 0 $$

(49)

$$ \tilde{\zeta }^{\prime}_{1} \left( {1,s} \right) = 0 $$

(50)

Equation 54 accounts for the no-flow boundary condition at the inclusion surface. The solution is presented as below:

$$ \tilde{\zeta }_{1} \left( {r,s} \right) = {\frac{q}{3rs}}\left[ {\cosh \left( {\sqrt s r} \right) - {\frac{{\cosh \left( {\sqrt s } \right) - \sqrt s \sinh \left( {\sqrt s } \right)}}{{\sqrt s \cosh \left( {\sqrt s } \right) - \sinh \left( {\sqrt s } \right)}}}\sinh \left( {\sqrt s r} \right)} \right]. $$

(51)

Thereafter, the radial displacement and stress components can be obtained in a method similar to what presented in Sect. 2. The results are given below:

$$ u_{r1} \left( {r,s} \right) = {\frac{{\gamma_{1} }}{{r^{2} }}}\int\limits_{0}^{r} {x^{2} \tilde{\zeta }_{1} \left( {x,s} \right){\text{d}}x} + {\frac{r}{3}}A_{1} \left( s \right) $$

(52)

$$ \tilde{\sigma }_{rr1} \left( {r,s} \right) = - {\frac{{2\gamma_{1} }}{{r^{3} }}}\int\limits_{0}^{r} {x^{2} \tilde{\zeta }_{1} \left( {x,s} \right){\text{d}}x} + {\frac{{\left( {1 + \nu_{u1} } \right)}}{{3\left( {1 - 2\nu_{u1} } \right)}}}A_{1} \left( s \right). $$

(53)

The radial displacement and stress components in the matrix can be simply found from the classical theory of elasticity. They are written as:

$$ \tilde{u}_{r2} \left( {R,s} \right) = {\frac{{A_{2} (s)}}{r}} $$

(54)

$$ \tilde{\sigma }_{rr2} \left( {R,s} \right) = - G{\frac{{2A_{2} (s)}}{{r^{2} }}}. $$

(55)

The arbitrary functions A ₁(s) and A ₂(s) are found from the following boundary conditions:

$$ \tilde{u}_{r1} \left( {1,s} \right) = \tilde{u}_{r2} \left( {1,s} \right) $$

(56)

$$ \tilde{\sigma }_{rr1} \left( {1,s} \right) = g\tilde{\sigma }_{rr1} \left( {1,s} \right). $$

(57)

That gives:

$$ A_{1} (s) = {\frac{{ \, 2q \, \gamma_{1} ( - 1 + g) \, ( - 1 + 2\nu_{u1} )}}{{ \, s^{2} [1 + g(2 - 4\nu_{u1} ) + \nu_{u1} ]}}} $$

(58)

$$ A_{2} (s) = - {\frac{{q\gamma_{1} \, ( - 1 + \nu_{u1} )}}{{s^{2} [1 + g(2 - 4\nu_{u1} ) + \nu_{u1} ]}}}. $$

(59)

Substitution of Eqs. 58 and 59 into Eq. 52 yields Eq. 28.

The expansion parameter defined in Sect. 3.2 can be found as:

$$ \eta_{\varepsilon } = {\frac{{3\gamma_{1} \left( {1 - \nu_{ul} } \right)}}{{\left[ {\left( {1 + \nu_{ul} } \right) + 2g\left( {1 - 2\nu_{ul} } \right)} \right]}}}. $$

(60)

The plot of Eq. 60 is given in Fig. 10. It shows that if the inclusion consists of incompressible constituents (ν _u1 = 0.5), the expansion would be the same as the loading efficiency parameter, where all curves meet at g = 1. The graph corresponding to ν _u1 = 0.33 has been generated before in Fig. 4 by the solid curve corresponding to an impermeable boundary (λ → 0).

Fig. 10

Variations of inclusion volume change with stiffness ratio at various undrained Poisson’s ratios of the inclusion surrounded by an elastic matrix