Skip to main content
SpringerLink
Log in

Stability of a linear oscillator with damping force of the fractional-order derivative

  • Research Paper
  • Published:
Science China Physics, Mechanics and Astronomy Aims and scope Submit manuscript

Abstract

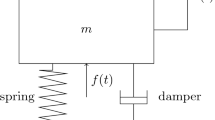
It begins with the study of damping representation of a linear vibration system of single degree of freedom (SDOF), from the view point of fractional calculus. By using the idea of stability switch, it shows that the linear term involving the fractional-order derivative of an order between 0 and 2 always acts as a damping force, so that the unique equilibrium is asymptotically stable. Further, based on the idea of stability switch again, the paper proposes a scheme for determining the stable gain region of a linear vibration system under a fractional-order control. It shows that unlike the classical velocity feedback which can adjust the damping force only, a fractional-order feedback can adjust not only the damping force, but also the elastic restoring force, and in addition, a fractional-order PD α control can either enlarge the stable gain region or narrow the stable gain region. For the dynamic systems described by integer-order derivatives, the asymptotical stability of an equilibrium is guaranteed if all characteristic roots stay in the open left half-plane, while for the systems with fractional-order derivatives, the asymptotical stability of an equilibrium is guaranteed if all characteristic roots stay within a sector in the complex plane. Analysis shows that the proposed method, based on the idea of stability switch, works effectively in the stability analysis of dynamical systems with fractional-order derivatives.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bagley R L, Torvik P J. On the appearance of the fractional derivative in the behavior of real materials. J Appl Mech, 1984, 51: 294–298

    Article  Google Scholar 

  2. Bagley R L, Torvik P J. Fractional calculus—A different approach to the analysis of viscoe1astically damped structures. AIAA J, 1983, 21: 741–748

    Article  MATH  ADS  Google Scholar 

  3. Bagley R L, Torvik P J. A theoretical basis for the application of fractional calculus to viscoelasticity. J Rheol. 1983, 27: 201–220

    Article  MATH  ADS  Google Scholar 

  4. Bagley R L, Torvik P J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J, 1985, 23: 918–925

    Article  MATH  ADS  Google Scholar 

  5. Bagley R L. Power law and fractional calculus model of viscoelasticity. AIAA J, 1989, 27: 1412–1417

    Article  ADS  Google Scholar 

  6. Ingman D, Suzdalnitsky J. Application of dynamic fractional differentiation to the study of oscillating viscoelastic medium with cylindrical cavity. J Vib Acoust, 2002, 124: 642–645

    Article  Google Scholar 

  7. Heymans N. Fractional calculus description of non-linear viscoelastic behavior of polymers. Nonlinear Dyn, 2004, 38: 221–231

    Article  MATH  Google Scholar 

  8. Adolfsson K. Nonlinear fractional order viscoelasticity at large strains. Nonlinear Dyn, 2004, 38: 233–246

    Article  MATH  MathSciNet  Google Scholar 

  9. Koeller R C. Toward an equation of state for solid materials with memory by use of the half-order derivative. Acta Mech, 2007, 191: 125–131

    Article  MATH  Google Scholar 

  10. Tong D K, Wang R H. Analysis of the flow of non-Newtonian viscoelastic fluids in fractal reservoir with the fractional derivative. Sci China Ser G-Phys Mech Astron, 2004, 47: 421–441

    Article  ADS  Google Scholar 

  11. Tong D K, Wang R H, Yang H S. Exact solutions for the flow of non-Newtonian fluid with fractional derivative in an annular pipe. Sci China Ser G-Phys Mech Astron, 2005, 48: 485–495

    Article  ADS  Google Scholar 

  12. Xu M Y, Tan W C. Intermediate processes and critical phenomena: Theory, method and progress of fractional operators and their applications to modern mechanics. Sci China Ser G-Phys Mech Astron, 2006, 49: 257–272

    Article  MATH  ADS  Google Scholar 

  13. Podlubny I. Fractional Differential Equations. San Diego: Academic Press, 1999

    MATH  Google Scholar 

  14. Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier, 2006

    MATH  Google Scholar 

  15. Das S. Functional Fractional Calculus for System Identification and Controls. Berlin: Springer-Verlag, 2008

    MATH  Google Scholar 

  16. Monje C A, Calderon A J, Vinagre B M, et al. On fractional PI λ controllers: Some tuning rules for robustness to plant uncertainties. Nonlinear Dyn, 2004, 38: 369–381

    Article  MATH  Google Scholar 

  17. Manabe S. A suggestion of fractional-order controller for flexible spacecraft attitude control. Nonlinear Dyn, 2004, 29: 251–268

    Article  Google Scholar 

  18. Lazarevic M P. Finite time stability of PD α fractional control of robotic time-delay systems. Mech Res Commun, 2006, 33: 269–279

    Article  MathSciNet  Google Scholar 

  19. Xue D, Zhao C, Chen Y. Fractional order PID control of a DC-motor with elastic shaft: A case study. American Control Conference, 2006, doi: 10.1109/ACC.2006.1657207

  20. Cervera J, Banos A, Monje C A, et al. Turning of fractional PID controllers by using QFT. IEEE, 2006, doi: 10.1109/IECON.2006. 348131

  21. Wang Z H, Zheng Y G. The optimal form of the fractional-order difference feedbacks in enhancing the stability of a SDOF vibration system. J Sound Vib, 2009, 326: 476–488

    Article  ADS  Google Scholar 

  22. Radwan A G, Soliman A M, Elwakli A S, et al. On the stability of linear systems with fractional-order elements. Chaos Solitons Fractals, 2009, 40: 2317–2328

    Article  Google Scholar 

  23. Mohammad S T, Mohammad H. A note on the stability of fractional order systems. Math Comput Simul, 2009, 79: 1566–1576

    Article  MATH  Google Scholar 

  24. Farshad M B, Masoud K G. An efficient numerical algorithm for stability testing of fractional-delay systems. ISA Trans, 2009, 48: 32–37

    Article  Google Scholar 

  25. Hwang C, Cheng Y C. A numerical algorithm for stability testing of fractional delay systems. Automatica, 2006, 42: 825–831

    Article  MATH  MathSciNet  Google Scholar 

  26. Wang Z B, Cao G Y, Zhu X J. Stability conditions and criteria for fractional order linear time-invariant systems (in Chinese). Control Theory Appl, 2004, 21: 922–926

    MATH  Google Scholar 

  27. Chen Y Q, Ahn H S, Podlubny I. Robust stability check of fractional order linear time invariant systems with interval uncertainties. Signal Process, 2006, 86: 2611–2618

    Article  MATH  Google Scholar 

  28. Bonilla B, Rivero M, Trujillo J J. Linear differential equations of fractional orders. In: Sabatier J, Agrawal O P, Tenreiro Machado J A, eds. Advances in Fractional Calculus. Dordrecht: Springer, 2007. 77–91

    Chapter  Google Scholar 

  29. Naber M. Linear fractionally damped oscillator. Int J Differ Equ, 2010, Doi: 10.1155/2010/197020

Download references

Author information

Authors and Affiliations

  1. Institute of Vibration Engineering Research, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    ZaiHua Wang & HaiYan Hu

  2. Institute of Science, PLA University of Science and Technology, Nanjing, 211101, China

    ZaiHua Wang

Authors
  1. ZaiHua Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. HaiYan Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to ZaiHua Wang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, Z., Hu, H. Stability of a linear oscillator with damping force of the fractional-order derivative. Sci. China Phys. Mech. Astron. 53, 345–352 (2010). https://doi.org/10.1007/s11433-009-0291-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11433-009-0291-y

Keywords

Search

Navigation