Skip to main content
SpringerLink
Log in

Bursting of Morris-Lecar neuronal model with current-feedback control

  • Published:
Science in China Series E: Technological Sciences Aims and scope Submit manuscript

Abstract

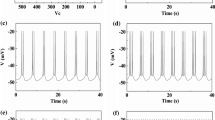
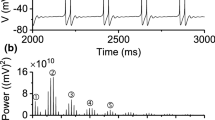
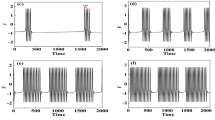
The Morris-Lecar (ML) neuronal model with current-feedback control is considered as a typical fast-slow dynamical system to study the combined influences of the reversal potential V Ca of Ca2+ and the feedback current I on the generation and transition of different bursting oscillations. Two-parameter bifurcation analysis of the fast subsystem is performed in the parameter (I, V Ca)-plane at first. Three important codimension-2 bifurcation points and some codimension-1 bifurcation curves are obtained which enable one to determine the parameter regions for different types of bursting. Next, we further divide the control parameter (V 0, V Ca)-plane into five different bursting regions, namely, the “fold/fold” bursting region R1, the “fold/Hopf” bursting region R2, the “fold/homoclinic” bursting region R3, the “subHopf/homoclinic” bursting region R4 and the “subHopf/subHopf” bursting region R5, as well as a silence region R6. Codimension-1 and -2 bifurcations are responsible for explanation of transition mechanisms between different types of bursting. The results are instructive for further understanding the dynamical behavior and mechanisms of complex firing activities and information processing in biological nervous systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Lisman J. Bursts as a unit of neural information: making unreliable synapses reliable. Trends Neurosci, 1997, 20(1): 38–43

    Article  Google Scholar 

  2. Reinagel P, Godwin D, Sherman S M, et al. Encoding of visual in- formation by LGN bursts. J Neurophysiol, 1999, 81: 2558–2569

    Google Scholar 

  3. Sherman S M. Tonic and burst firing: dual modes of thalamocortical relay. Trends Neurosci, 2001, 24(2): 122–126

    Article  MathSciNet  Google Scholar 

  4. Izhikevich E M. Bursts as a unit of neural information: selective communication via resonance. Trends Neurosci, 2003, 26(2): 161–167

    Article  Google Scholar 

  5. Rinzel J. Bursting oscillations in an excitable membrane model. In: Sleeman B D, Jarvis R J, eds. Ordinary and Partial Differential Equtations. New York: Springer-Verlag, 1985. 304–316

    Chapter  Google Scholar 

  6. Terman D. Chaotic spikes arising from a model for bursting in excitable membrane models. SIAM J Appl Math, 1991, 51(11): 1418–1450

    Article  MATH  MathSciNet  Google Scholar 

  7. Terman D. The transition from bursting to continuous spiking in excitable membrane models. J Nonlinear Sci, 1992, 2(2): 133–182

    Article  MathSciNet  Google Scholar 

  8. Wang X J. Genesis of bursting oscillations in the Hindmarsh-Rose model and homoclinicity to a chaotic saddle. Physica D, 1993, 62(2): 263–274

    Article  MATH  MathSciNet  Google Scholar 

  9. Belykh V N, Belykh I V, Colding-Jorgensen M, et al. Homoclinic bifurcations leading to the emergence of bursting oscillations in cell models. Eur Phys J E, 2000, 3(2): 205–219

    Article  Google Scholar 

  10. Guckenheimer J, Tien J H. Bifurcation in the fast dynamics of neurons: implication for bursting. In: Coombes S, Bressloff P C, eds. The Genesis of Rhythm in the Nervous System. Bursting: World Scientific Publish, 2005. 89–122

    Google Scholar 

  11. Shorten P R, Wall D J. A Hodgkin-Huxley model exhibiting bursting oscillations. Bull Math Biol, 2000, 62(6): 695–715

    Article  Google Scholar 

  12. Bertram R, Butte M, Kiemel T, et al. Topological and phenomenological classification of bursting oscillations. Bull Math Biol, 1995, 57(4): 413–439

    MATH  Google Scholar 

  13. Xie Y, Duan Y B, Xu J X, et al. Parabolic bursting induced by veratridine in rat injured sciatic nerves. ACTA Bioch Bioph Sin, 2003, 35(9): 806–810

    Google Scholar 

  14. Yang Z Q, Lu Q S. Different types of bursting in Chay neuronal model. Sci China Ser G-Phys Mech Astron, 2008, 51(6): 687–698

    Article  MathSciNet  Google Scholar 

  15. Channell P, Cymbalyuk G, Shilnikov A. Origin of bursting through homoclinic spike adding in a neuron model. Phys Rev Lett, 2007, 98(13): 134101

    Google Scholar 

  16. Ibarz B, Cao H J, Sanjuán, M A F. Bursting regimes in map-based neuron models coupled through fast threshold modulation. Phys Rev E, 2008, 77(5–1): 051918

  17. Shen Y, Hou Z H, Xin H W. Transition to burst synchronization in coupled neuron networks. Phys Rev E, 2008, 77(3-1): 031920

    Google Scholar 

  18. Duan L X, Lu Q S, Wang Q Y. Two-parameter bifurcation analysis of firing activities in the Chay neuronal model. Neurocomp, 2008. doi:10.1016/j.neucom.2008.01.019

  19. Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J, 1981, 35(2): 193–213

    Article  Google Scholar 

  20. Izhikevich E M. Neural excitability, spiking and bursting. Int J Bifurcat Chaos, 2000, 10(10): 1171–1266

    MATH  MathSciNet  Google Scholar 

  21. Tsumoto K, Kitajima H. Bifurcation in Morris-Lecar neuron model. Neurocomp, 2006, 69(2): 293–316

    Article  Google Scholar 

  22. Hoppensteadt F C, Izhikevich E M. Weakly Connected Neural Networks. New York: Springer-Verlag, 1997

    Google Scholar 

  23. Ghigliazza R M, Holmes P. Minimal models of bursting neurons: how multiple currents, conductances, and time scales affect bifurcation diagrams. SIAM J Appl Dyn Syst, 2004, 3(4): 636–667

    Article  MATH  MathSciNet  Google Scholar 

  24. Ermentrout G B. Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students. Philadelphia: SIAM, 2002

    MATH  Google Scholar 

  25. Kuznetsov Y A. Elements of Applied Bifurcation Theory. New York: Springer-Verlag, 1995. 253–265

    MATH  Google Scholar 

  26. Kuznetsov Y A, Levitin V V. Content-1.5-ibmpc-mswin-bcc55. zip. http://www.math.uu.nl/people/kuznet/CONTENT

  27. Holden L, Erneux T. Slow passage through a Hopf bifurcation: Form oscillatory to steady state solutions. SIAM J Appl Math, 1993 (53): 1045–1058

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Science, North China University of Technology, Beijing, 100144, China

    LiXia Duan

  2. School of Science, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    QiShao Lu

  3. Institute of Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    DaiZhan Cheng

Authors
  1. LiXia Duan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. QiShao Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. DaiZhan Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to QiShao Lu.

Additional information

Supported by the National Natural Science Foundation of China (Grant Nos. 10872014 and 10702002)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Duan, L., Lu, Q. & Cheng, D. Bursting of Morris-Lecar neuronal model with current-feedback control. Sci. China Ser. E-Technol. Sci. 52, 771–781 (2009). https://doi.org/10.1007/s11431-009-0040-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-009-0040-5

Keywords

Search

Navigation