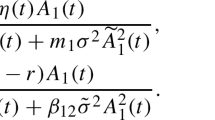Skip to main content
SpringerLink
Log in

Optimal Reinsurance and Dividend Under Model Uncertainty

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

In this paper, the authors analyze the optimal reinsurance and dividend problem with model uncertainty for an insurer. Here the model uncertainty represents possible deviations between the real market and the assumed model. In addition to the incorporation of model uncertainty into the traditional diffusion surplus process, the authors include a penalty function in the objective function. The proposed goal is to find the optimal reinsurance and dividend strategy that maximizes the expected discounted dividend before ruin in the worst case of all possible scenarios, namely, the worst market. Using a dynamic programming approach, the problem is reduced to solving a Hamilton-Jacob-Bellman-Isaac (HJBI) equation with singular control. This problem is more difficult than the traditional robust control or singular control problem. Here, the authors prove that the value function is the unique solution to this HJBI equation with singular control. Moreover, the authors present a verification theorem when a smooth solution can be found, and derive closed-form solution when the function in the objective function is specified.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. De Finetti B, Su un-impostazione alternativa della teoria collettiva del rischio, Transactions of the XVth International Congress of Actuaries, 1957, 2: 433–443.

    Google Scholar 

  2. Hogaard B and Taksar M, Controlling risk exposure and dividends payout schemes: Insurance company example, Mathematical Finance, 1999, 9: 153–182.

    Article  MathSciNet  MATH  Google Scholar 

  3. Choulli T, Taksar M, and Zhou X Y, A diffusion model for optimal dividend distribution for a company with constrains on risk control, SIAM Journal on Control and Optimization, 2003, 41: 1946–1979.

    Article  MathSciNet  MATH  Google Scholar 

  4. Cadenillas A, Choulli T, Taksar M, et al., Classical and impulse stochastic control for the optimization of the dividend and risk policies of an insurance firm, Mathematical Finance, 2006, 16: 181–202.

    Article  MathSciNet  MATH  Google Scholar 

  5. Gerber H U and Shiu E S W, On optimal dividend strategies in the compound Poisson model, North American Actuarial Journal, 2006, 10: 76–93.

    Article  MathSciNet  MATH  Google Scholar 

  6. Yuen K C, Wang G, and Li W K, The Gerber—Shiu expected discounted penalty function for risk processes with interest and a constant dividend barrier, Insurance: Mathematics and Economics, 2007, 40: 104–112.

    MathSciNet  MATH  Google Scholar 

  7. He L and Liang Z X, Optimal financing and dividend control of the insurance company with proportional reinsurance policy, Insurance: Mathematics and Economics, 2008, 42: 976–983.

    MathSciNet  MATH  Google Scholar 

  8. Bai L H, Guo J Y, and Zhang H Y, Optimal excess-of-loss reinsurance and dividend payments with both transaction costs and taxes, Quantitative Finance, 2010, 10: 1163–1172.

    Article  MathSciNet  MATH  Google Scholar 

  9. Wei J Q, Yang H L, and Wang R M, Optimal reinsurance and dividend strategies under the Markov-modulated insurance risk model, Stochastic Analysis and Applications, 2010, 28: 1078–1105.

    Article  MathSciNet  MATH  Google Scholar 

  10. Meng H and Siu T K, On optimal reinsurance, dividend and reinvestment strategies, Economic Modelling, 2011, 28: 211–218.

    Article  Google Scholar 

  11. Meng H and Siu T K, Optimal mixed impulse-equity insurance control problem with reinsurance, SIAM Journal on Control and Optimization, 2011, 49(1): 254–279.

    Article  MathSciNet  MATH  Google Scholar 

  12. Chen M, Peng X, and Guo J, Optimal dividend problem with a nonlinear regular-singular stochastic control, Insurance: Mathematics and Economics, 2013, 52: 448–456.

    MathSciNet  MATH  Google Scholar 

  13. Yin C C and Yuen K C, Optimal dividend problems for a jump-diffusion model with capital injections and proportional transaction costs, Journal of Industrial and Management Optimization, 2015, 11: 1247–1262.

    Article  MathSciNet  MATH  Google Scholar 

  14. Chen M and Yuen K C, Optimal dividend and reinsurance in the presence of two reinsurers, Journal of Applied Probability, 2016, 53: 554–571.

    Article  MathSciNet  MATH  Google Scholar 

  15. Zhou M and Yuen K C, Optimal reinsurance and dividend for a diffusion model with capital injection: Variance premium principle, Economic Modelling, 2012, 29: 198–207.

    Article  Google Scholar 

  16. Jeffreys H, Theory of Probability (3rd Ed.), Oxford University Press, Oxford, 1961.

    MATH  Google Scholar 

  17. Cairns A J G, A discussion of parameter and model uncertainty in insurance, Insurance: Mathematics and Economics, 2000, 27: 313–330.

    MATH  Google Scholar 

  18. Mataramvura S and Øksendal B, Risk minimizing portfolios and HJBI equations for stochastic differential games, Stochastics: An International Journal of Probability and Stochastics Processes, 2008, 80: 317–337.

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhang X and Siu T K, Optimal investment and reinsurance of an insurer with model uncertainty, Insurance: Mathematics and Economics, 2009, 45: 81–88.

    MathSciNet  MATH  Google Scholar 

  20. Korn R, Menkens O, and Steffensen M, Worst-case-optimal dynamic reinsurance for large claims, European Actuarial Journal, 2012, 2: 21–48.

    Article  MathSciNet  MATH  Google Scholar 

  21. Liu J, Yiu K F C, and Siu T K, Optimal investment of an insurer with regime-switching and risk constraint, Scandinavian Actuarial Journal, 2014, 2014: 583–601.

    Article  MathSciNet  MATH  Google Scholar 

  22. Hansen L and Sargent T, Discounted linear exponential quadratic gaussian control, IEEE Transactions on Automatic Control, 1995, 40: 968–971.

    Article  MathSciNet  MATH  Google Scholar 

  23. Anderson E W, Hansen L P, and Sargent T J, A quartet of semi-groups for model specification, robustness, prices of risk, and model detection, Journal of the European Economic Association, 2003, 1: 68–123.

    Article  Google Scholar 

  24. Maenhout P J, Robust portfolio rules and asset pricing, The Review of Financial Studies, 2004, 17: 951–983.

    Article  Google Scholar 

  25. Maenhout P J, Robust portfolio rules and detection-error probabilities for a mean-reverting risk premium, Journal of Economic Theory, 2006, 128: 136–163.

    Article  MathSciNet  MATH  Google Scholar 

  26. Branger N, Larsen L S, and Munk C, Robust portfolio choice with ambiguity and learning about return predictability, Journal of Banking and Finance, 2013, 37: 1397–1411.

    Article  Google Scholar 

  27. Yi B, Li Z, Viens F, et al., Robust optimal control for an insurer with reinsurance and investment under Heston’s stochastic volatility model, Insurance: Mathematics and Economics, 2013, 53: 601–614.

    MathSciNet  MATH  Google Scholar 

  28. Yi B, Viens F, Li Z F, et al., Robust optimal strategies for an insurer with reinsurance and investment under benchmark and mean-variance criteria, Scandinavian Actuarial Journal, 2015, 8: 725–751.

    Article  MathSciNet  MATH  Google Scholar 

  29. Zeng Y, Li D, and Gu A, Robust equilibrium reinsurance-investment strategy for a mean-variance insurer in a model with jumps, Insurance: Mathematics and Economics, 2016, 66: 138–152.

    MathSciNet  MATH  Google Scholar 

  30. Grandell J, Aspects of Risk Theory, Springer, Berlin, 1990.

    MATH  Google Scholar 

  31. Browne S, Optimal investment policies for a firm with a random risk process: Exponential utility and minimizing the probability of ruin, Mathematics of Operation Research, 1995, 20: 937–958.

    Article  MathSciNet  MATH  Google Scholar 

  32. Asmussen S and Taksar M, Controlled diffusion models for optimal dividend pay-out, Insurance: Mathematics and Economics, 1997, 20: 1–15.

    MathSciNet  MATH  Google Scholar 

  33. Promislow S D and Young V R, Minimizing the probability of ruin when claims follow Brownian Motion with drift, North American Actuarial Journal, 2005, 9: 110–128.

    Article  MathSciNet  MATH  Google Scholar 

  34. Duffie D and Epstein L G, Stochstic Differential Utility, Econometrica, 1992, 60: 353–394.

    Article  MathSciNet  MATH  Google Scholar 

  35. Cohen S N and Elliott R J, Stochastic Calculus and Applications (2nd Ed.), Birkhäuser, Basel, 2015.

    Book  MATH  Google Scholar 

  36. Fleming W H and Soner M, Controlled Markov Processes and Viscosity Solutions (2nd Ed.), Springer Science & Business Media, Berlin, 2006.

    MATH  Google Scholar 

  37. Crandall M G and Lions P L, Viscosity solutions of Hamilton—Jacobi equations, Transactions of the American Mathematical Society, 1983, 277: 1–42.

    Article  MathSciNet  MATH  Google Scholar 

  38. Crandall M G, Ishii H, and Lions P L, User’s guide to viscosity solutions of second order partial differential equations, Bulletin of the American Mathematical Society, 1992, 27: 1–67.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. China Institute for actuarial science, Central University of Finance and Economics, Beijing, 100081, China

    Jingzhen Liu & Yike Wang

  2. School of Finance & Chinese Fintech Research Center, Central University of Finance and Economics, Beijing, 100081, China

    Ning Zhang

Authors
  1. Jingzhen Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yike Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ning Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jingzhen Liu.

Additional information

This research was supported by the National Natural Science Foundation of China under Grant No. 11771466, and Program for Innovation Research under Grant No. 20170074 and the Emerging Interdisciplinary Project of CUFE.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, J., Wang, Y. & Zhang, N. Optimal Reinsurance and Dividend Under Model Uncertainty. J Syst Sci Complex 36, 1116–1143 (2023). https://doi.org/10.1007/s11424-023-1237-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-023-1237-6

Keywords

Search

Navigation