Skip to main content
SpringerLink
Log in

Quantum Algorithm Design: Techniques and Applications

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

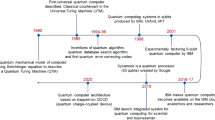
In recent years, rapid developments of quantum computer are witnessed in both the hardware and the algorithm domains, making it necessary to have an updated review of some major techniques and applications in quantum algorithm design.

In this survey as well as tutorial article, the authors first present an overview of the development of quantum algorithms, then investigate five important techniques: Quantum phase estimation, linear combination of unitaries, quantum linear solver, Grover search, and quantum walk, together with their applications in quantum state preparation, quantum machine learning, and quantum search. In the end, the authors collect some open problems influencing the development of future quantum algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Benioff P, The computer as a physical system, Journal of Statistical Physics, 1980, 22: 563–591.

    Article  MathSciNet  MATH  Google Scholar 

  2. Feynman R, Simulating physics with computers, International Journal of Theoretical Physics, 1982, 21: 467–488.

    Article  MathSciNet  Google Scholar 

  3. Deutsch D, Quantum theory, the Church-Turing principle and the universal quantum computer, Proc. R. Soc. A, 1985, 400: 97–117.

    Article  MathSciNet  MATH  Google Scholar 

  4. Deutsch D, Quantum computational networks, Proc. R. Soc. A, 1989, 425: 73–90.

    Article  MathSciNet  MATH  Google Scholar 

  5. Yao A C-C, Quantum circuit complexity, Proc. FOCS 1993, IEEE, Palo Alto, 1993, 352–361.

    Google Scholar 

  6. Bernstein E and Vazirani U V, Quantum complexity theory, SIAM J. Comput., 1997, 26(5): 1411–1473.

    Article  MathSciNet  MATH  Google Scholar 

  7. Deutsch D and Jozsa R, Rapid solution of problems by quantum computation, Proc. R. Soc. A, 1992, 439: 553–558.

    Article  MathSciNet  MATH  Google Scholar 

  8. Simon D R, On the power of quantum computation, SIAM J. Comput., 1997, 26(5): 1474–1483.

    Article  MathSciNet  MATH  Google Scholar 

  9. Shor P W, Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer, SIAM J. Comput., 1997, 26(5): 1484–1509.

    Article  MathSciNet  MATH  Google Scholar 

  10. Kitaev A Y, Quantum measurements and the abelian stabilizer problem, arXiv: quant-ph /9511026.

  11. Ettinger M, Høyer P, and Knill E, The quantum query complexity of the hidden subgroup problem is polynomial, Information Processing Letters, 2004, 91(1): 43–48.

    Article  MathSciNet  MATH  Google Scholar 

  12. Nielsen M A and Chuang I L, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, 2000.

    MATH  Google Scholar 

  13. Hallgren S, Polynomial-time quantum algorithms for Pell’s equation and the principal ideal problem, Proc. STOC 2002, ACM Press, New York, 2002, 653–658.

    Google Scholar 

  14. Proos J and Zalka C, Shor’s discrete logarithm quantum algorithm for elliptic curves, Quantum Information and Computation, 2003, 3: 317–344.

    MathSciNet  MATH  Google Scholar 

  15. Bacon D, Childs A M, and van Dam W, From optimal measurement to efficient quantum algorithms for the hidden subgroup problem over semidirect product groups, Proc. FOCS 2005, IEEE, Washington, 2005, 469–478.

    Google Scholar 

  16. Chi D P, Kim J S, and Lee S, Notes on the hidden subgroup problem on some semi-direct product groups, Phys. Lett. A, 2006, 359(2): 114–116.

    Article  MATH  Google Scholar 

  17. Inui Y and Le Gall G, Efficient quantum algorithms for the hidden subgroup problem over a class of semi-direct product groups, Quantum Information and Computation, 2007, 7(5 & 6): 559–570.

    MathSciNet  MATH  Google Scholar 

  18. Kuperberg G, A subexponential-time quantum algorithm for the dihedral hidden subgroup problem, SIAM J. Comput., 2005, 35(1): 170–188.

    Article  MathSciNet  MATH  Google Scholar 

  19. Moore C, Rockmore D, Russell A, et al., The power of basis selection in Fourier sampling: The hidden subgroup problem in affine groups, Proc. SODA 2004, SIAM, Philadelphia, 2004, 1113–1122.

    Google Scholar 

  20. Gavinsky D, Quantum solution to the hidden subgroup problem for poly-near-Hamiltoniangroups, Quantum Information and Computation, 2004, 4: 229–235.

    MathSciNet  MATH  Google Scholar 

  21. Hallgren S, Russell A, and Ta-Shma A, Normal subgroup reconstruction and quantum computation using group representations, SIAM J. Comput., 2003, 32(4): 916–934.

    Article  MathSciNet  MATH  Google Scholar 

  22. Ivanyos G, Magniez F, and Santha M, Efficient quantum algorithms for some instances of the non-abelian hidden subgroup problem, SPAA 2001, ACM Press, New York, 2001, 263–270.

    Google Scholar 

  23. Grigni M, Schulman L, Vazirani M, et al., Quantum mechanical algorithms for the nonabelian hidden subgroup problem, Combinatorica, 2004, 24: 137–154.

    Article  MathSciNet  MATH  Google Scholar 

  24. van Dam W, Hallgren S, and Ip L, Quantum algorithms for some hidden shift problems, SIAM J. Comput., 2006, 36(3): 763–778.

    Article  MathSciNet  MATH  Google Scholar 

  25. Boneh D and Lipton R J, Algorithms for black-box fields and their application to cryptography, Advances in Cryptology — CRYPTO’96, Ed. by Koblitz N, LNCS 1109, 1996, 283–297.

    Google Scholar 

  26. Kuwakado H and Morii M, Quantum distinguisher between the 3-round Feistel cipher and the random permutation, Proc. ISIT 2010, IEEE, Austin, TX, 2010, 2682–2685.

    Google Scholar 

  27. Kuwakado H and Morii M, Security on the quantum-type Even-Mansour cipher, Proc. ISITA 2012, IEEE, Honolulu, HI, 2012, 312–316.

    Google Scholar 

  28. Santoli T and Schaffner C, Using Simon’s algorithm to attack symmetric-key cryptographic primitives, arXiv: 1603.07856 [quant-ph].

  29. Kaplan M, Leurent G, and Leverrier A, Breaking symmetric cryptosystems using quantum period finding, arXiv: 1602.05973v3 [quant-ph].

  30. Ajtai M and Dwork C, A public-key cryptosystem with worst-case/average-case equivalence, Proc. STOC 1997, ACM Press, New York, 1997, 284–293.

    Google Scholar 

  31. Regev O, New lattice-based cryptographic constructions, Journal of the ACM, 2004, 51(6): 899–942.

    Article  MathSciNet  MATH  Google Scholar 

  32. Regev O, Quantum computation and lattice problems, SIAM J. Comput., 2004, 33(3): 738–760.

    Article  MathSciNet  MATH  Google Scholar 

  33. Galbraith S and Stolbunov A, Improved algorithm for the isogeny problem for ordinary elliptic curves, Applicable Algebra in Engineering, Communication and Computing, 2013, 24(2): 107–131.

    MathSciNet  MATH  Google Scholar 

  34. Couveignes J M, Hard Homogeneous Spaces, https://eprint.iacr.org/2006/291.pdf.

  35. Rostovtsev A and Stolbunov A, Public-key cryptosystem based on isogenies, https://eprint.iacr.org/2006/145.pdf.

  36. Stolbunov A, Constructing public-key cryptographic schemes based on class group action on a set of isogenous elliptic curves, Adv. Math. Commun., 2010, 4(2): 215–235.

    Article  MathSciNet  MATH  Google Scholar 

  37. Childs A M, Jao D, and Soukharev V, Constructing elliptic curve isogenies in quantum subexponential time, J. Mathematical Cryptology, 2014, 8: 1–29.

    Article  MathSciNet  MATH  Google Scholar 

  38. Grover L K, A fast quantum mechanical algorithm for database search, Proc. STOC 1996, ACM Press, New York, 1996, 212–219.

    Google Scholar 

  39. Bennett C H, Bernstein E, Brassard G, et al., Strengths and weaknesses of quantum computing, SIAM J. Comput., 1997, 26(5): 1510–1523.

    Article  MathSciNet  MATH  Google Scholar 

  40. Zalka C, Grover’s quantum searching algorithm is optimal, Phy. Rev. A, 1999, 60: 2746–2751.

    Article  Google Scholar 

  41. Long G L, Grover algorithm with zero theoretical rate, Phys. Lett. A, 2001, 64: 022307.

    Google Scholar 

  42. Ambainis A, Quantum search algorithms, SIGACT News, 2004, 35(2): 22–35.

    Article  Google Scholar 

  43. Campbell E, Khurana A, and Montanaro A, Applying quantum algorithms to constraint satisfaction problems, arXiv: 1810.05582 [quant-ph].

  44. Liu W Z, Zhang J F, and Long G L, A parallel quantum algorithm for the satisfiability problem, Common. Theor. Phys., 2008, 49(3): 629–630.

    Article  MATH  Google Scholar 

  45. Laarhoven T, Mosca M, and van de Pol J, Solving the shortest vector problem in lattices faster using quantum search, PQCrypto 2013, Ed. by Gaborit P, LNCS 7932, Springer, Berlin, Heidelberg, 2013, 83–101, also available: arXiv: 1301.6176v1 [cs.CR].

    Google Scholar 

  46. Faugère J C, Horan K, Kahrobaei D, et al., Fast quantum algorithm for solving multivariate quadratic equations, arXiv: 1712.07211 [cs.CR].

  47. He X Y, Sun X M, Yang G, et al., Exact quantum query complexity of weight decision problems, arXiv: 1801.05717v1 [quant-ph].

  48. Le Gall F and Nishimura H, Quantum algorithms for matrix products over semirings, Chicago Journal of Theoretical Computer Science, 2017, 1: 1–25.

    Article  MathSciNet  MATH  Google Scholar 

  49. Dürr C and Høyer P, A quantum algorithm for finding the minimum, arXiv: quant-ph/9607014.

  50. Kowada L A B, Lavor C, Portugal R, et al., A new quantum algorithm for solving the minimum searching problem, International Journal of Quantum Information, 2008, 6(3): 427–436.

    Article  MATH  Google Scholar 

  51. Brassard G, Høyer P, and Tapp A, Quantum Counting, Automata, Languages and Programming, Eds. by Larsen K G, et al., LNCS 1443, Springer, Berlin, Heidelberg, 1998, 820–831.

  52. Brassard G, Høyer P, and Mosca M, Quantum amplitude amplification and estimation, Quantum Computation and Quantum Information, 2002, 305: 53–74.

    Article  MathSciNet  MATH  Google Scholar 

  53. Brassard G, Høyer P, and Tapp A, Quantum cryptanalysis of hash and claw-free functions, LATIN’98: Theoretical Informatics, Eds. by Lucchesi C L and Moura A V, LNCS 1380, Springer, Berlin, Heidelberg, 1998, 163–169.

    Chapter  Google Scholar 

  54. Aaronson S and Shi Y, Quantum lower bounds for the collision and the element distinctness problems, Journal of the ACM, 2004, 51(4): 595–605.

    Article  MathSciNet  MATH  Google Scholar 

  55. Wang X, Yao A, and Yao F, Cryptanalysis on SHA-1, http://csrc.nist.gov/groups/ST/hash/documents/Wang SHA1-New-Result.pdf.

  56. Cochran M, Notes on the Wang, et al. 263 SHA-1 Differential Path, https://eprint.iacr.org/2007/474.pdf.

  57. Hoffstein J, Pipher J, and Silverman J H, NTRU: A ring-based public key cryptosystem, Algorithmic Number Theory, Ed. by Buhler J P, LNCS 1423, Springer, Berlin, Heidelberg, 1998, 267–288.

    Chapter  Google Scholar 

  58. Fluhrer S, Quantum cryptanalysis of NTRU, Cryptology ePrint Archive: Report 2015/676, 2015.

    Google Scholar 

  59. Childs A M, Universal computation by quantum walk, Phys. Rev. Lett., 2009, 102: 180501.

    Article  MathSciNet  Google Scholar 

  60. Magniez F, Santha M, and Szegedy M, Quantum algorithms for the triangle problem, SIAM J. Comput., 2007, 37(2): 413–424.

    Article  MathSciNet  MATH  Google Scholar 

  61. Jeffery S, Kothari R, and Magniez F, Nested quantum walks with quantum data structures, Proc. SODA 2013, SIAM, Philadelphia, 2013, 1474–1485.

    Google Scholar 

  62. Belovs A and Reichardt B W, Span programs and quantum algorithms for st-connectivity and claw detection, European Symp. on Algorithms, Eds. by Epstein L, et al., LNCS 7501, Springer, Berlin, Heidelberg, 2012, 193–204.

    MATH  Google Scholar 

  63. Buhrman H, Cleve R, de Wolf R, et al., Bounds for small-error and zero-error quantum algorithms, Proc. FOCS 1999, IEEE, New York, 1999, 358–368.

    Google Scholar 

  64. Dürr C, Heiligman M, and Høyer P, Quantum query complexity of some graph problems, SIAM J. Comput., 2006, 35(6): 1310–1328.

    Article  MathSciNet  MATH  Google Scholar 

  65. Ambainis A, Kempe J, and Rivosh A., Coins make quantum walks faster, Proc. SODA 2005, SIAM, Philadelphia, 2005, 1099–1108.

    Google Scholar 

  66. Tulsi A, Faster quantum-walk algorithm for the two-dimensional spatial search, Phys. Rev. A, 2008, 78: 012310.

    Article  MATH  Google Scholar 

  67. Magniez F, Nayak A, Richter P C, et al., On the hitting times of quantum versus random walks, Algorithmica, 2012, 63(1): 91–116.

    Article  MathSciNet  MATH  Google Scholar 

  68. Aaronson S and Ambainis A, Quantum search of spatial regions, Theory of Computing, 2005, 1: 47–79.

    Article  MathSciNet  MATH  Google Scholar 

  69. Childs A M, Cleve R, Jordan S P, et al., Discrete-query quantum algorithm for NAND trees, Theory of Computing, 2009, 5: 119–123.

    Article  MathSciNet  MATH  Google Scholar 

  70. Ambainis A, Childs A M, Reichardt B W, et al., Any AND-OR formula of size N can be evaluated in time n 1/2+o(1) on a quantum computer, SIAM J. Comput., 2010, 39(6): 2513–2530.

    Article  MathSciNet  MATH  Google Scholar 

  71. Reichardt B W, Faster quantum algorithm for evaluating game trees, Proc. SODA 2011, SIAM, Philadelphia, 2011, 546–559.

    Google Scholar 

  72. Reichardt B W, Reflections for quantum query algorithms, Proc. SODA 2011, SIAM, Philadelphia, 2011, 560–569.

    Google Scholar 

  73. Reichardt B W and Spalek R, Span-program-based quantum algorithm for evaluating formulas, Theory of Computing, 2012, 8: 291–319.

    Article  MathSciNet  MATH  Google Scholar 

  74. Childs A M and Kothari R, Quantum query complexity of minor-closed graph properties, SIAM Journal on Computing, 2012, 41(6): 1426–1450.

    Article  MathSciNet  MATH  Google Scholar 

  75. Le Gall F, Improved quantum algorithm for triangle finding via combinatorial arguments, Proc. FOCS 2014, IEEE, Philadelphia, 2014, 216–225.

    Google Scholar 

  76. Lee T, Magniez F, and Santha M, Improved quantum query algorithms for triangle finding and associativity testing, Algorithmica, 2017, 77: 459–486.

    Article  MathSciNet  MATH  Google Scholar 

  77. Bernstein D J, Jeffery S, Lange T, et al., Quantum algorithms for the subset-sum problem, Post-Quantum Cryptography, Ed. by Gaborit P, LNCS 7932, Springer, Berlin, Heidelberg, 2013, 16–33.

    Chapter  MATH  Google Scholar 

  78. Ambainis A, Quantum walk algorithm for element distinctness, SIAM J. Comput., 2007, 37: 210–239.

    Article  MathSciNet  MATH  Google Scholar 

  79. Magniez F and Nayak A, Quantum complexity of testing group commutativity, Algorithmica, 2007, 48(3): 221–232.

    Article  MathSciNet  MATH  Google Scholar 

  80. Buhrman H and Spalek R, Quantum verification of matrix products, Proc. SODA 2006, SIAM, Philadelphia, 2006, 880–889.

    Google Scholar 

  81. Le Gall F, Improved output-sensitive quantum algorithms for Boolean matrix multiplication, Proc. SODA 2012, SIAM, Philadelphia, 2012, 1464–1476.

    Google Scholar 

  82. Dorn S and Thierauf T, The quantum query complexity of algebraic properties, Fundamentals of Computation Theory, Eds. by Csuhaj-Varjú E, et al, LNCS 4639, Springer, Berlin, Heidelberg, 2007, 250–260.

    Chapter  MATH  Google Scholar 

  83. Feynman R, Quantum mechanical computer, Optics News, 1985, 11: 11–20.

    Article  Google Scholar 

  84. Chase B A and Landhal A J, Universal quantum walks and adiabatic algorithms by 1d Hamiltonians, arXiv: 0802.1207 [quant-ph].

  85. Farhi E and Gutmann S, Quantum computation and decision trees, Phys. Rev. A, 1998, 58: 915–928.

    Article  MathSciNet  Google Scholar 

  86. Meyer D, From quantum cellular automata to quantum lattice gases, J. Stat. Phys., 1996, 85: 551–574.

    Article  MathSciNet  MATH  Google Scholar 

  87. Nayak A and Vishvanath A, Quantum walk on the line, arXiv: quant-ph/0010117.

  88. Strauch F W, Connecting the discrete and continuous-time quantum walks, Phys. Rev. A, 2006, 74: 030301.

    Article  MathSciNet  Google Scholar 

  89. Childs A M, On the relationship between continuous- and discrete-time quantum walk, Communications in Mathematical Physics, 2010, 294(2): 581–603.

    Article  MathSciNet  MATH  Google Scholar 

  90. Ambainis A, Bach E, Nayak A, et al., One-dimensional quantum walks, Proc. STOC 2001, ACM Press, New York, 2001, 37–49.

    Google Scholar 

  91. Kempe J, Discrete quantum walks hit exponentially faster, Probability Theory and Related Fields, 2005, 133(2): 215–235.

    Article  MathSciNet  MATH  Google Scholar 

  92. Shenvi N, Kempe J, and Whaley K B, A quantum random-walk search algorithm, Phys. Rev. A, 2003, 67: 052307.

    Article  Google Scholar 

  93. Childs A M, Cleve R, Deotto E, et al., Exponential algorithmic speedup by quantum walk, Proc. STOC 2003, ACM Press, New York, 2003, 59–68.

    Google Scholar 

  94. Childs A M, Farhi E, and Gutmann S, An example of the difference between quantum and classical random walks, Quantum Inf. Process, 2002, 1(1 & 2): 35–43.

    Article  MathSciNet  MATH  Google Scholar 

  95. Szegedy M, Quantum speed-up of markov chain based algorithms, Proc. FOCS 2004, IEEE, Rome, 2004, 32–41.

    Google Scholar 

  96. Magniez F, Nayak A, Roland J, et al., Search via quantum walk, SIAM J. Comput., 2011, 40(1): 142–164.

    Article  MathSciNet  MATH  Google Scholar 

  97. Childs A M, Jeffery S, Kothari R, et al., A time-efficient quantum walk for 3-distinctness using nested updates, arXiv: 1302.7316 [quant-ph].

  98. Farhi E, Goldstone J, and Gutmann S, A quantum algorithm for the Hamiltonian NAND tree, Theory of Computing, 2008, 4: 169–190.

    Article  MathSciNet  MATH  Google Scholar 

  99. Harrow A W, Hassidim A, and Lloyd S, Quantum algorithm for solving linear systems of equations, Phys. Rev. Lett., 2009, 103(15): 150502.

    Article  MathSciNet  Google Scholar 

  100. Lloyd S, Universal quantum simulators, Science, 1996, 273(5278): 1073–1078.

    Article  MathSciNet  MATH  Google Scholar 

  101. Suzuki M, General theory of fractal path integrals with applications to many-body theories and statistical physics, Journal of Mathematical Physics, 1991, 32(2): 400–407.

    Article  MathSciNet  MATH  Google Scholar 

  102. Aharonov D and Ta-Shma A, Adiabatic quantum state generation and statistical zero knowledge, Proc. STOC 2003, ACM Press, New York, 2003, 20–29.

    Google Scholar 

  103. Berry D W, Ahokas G, Cleve R, et al., Efficient quantum algorithms for simulating sparse Hamiltonians, Comm. Math. Phys., 2007, 270(2): 359–371.

    Article  MathSciNet  MATH  Google Scholar 

  104. Childs A M and Kothari R, Simulating sparse Hamiltonians with star decompositions, Theory of Quantum Computation, Communication, and Cryptography, Eds. by van Dam W, et al., LNCS 6519, Springer-Verlag Berlin Heidelberg, 2011, 94–103.

    Chapter  Google Scholar 

  105. Berry D W and Childs A M, Black-box Hamiltonian simulation and unitary implementation, Quantum Information and Computation, 2012, 12: 29–62.

    MathSciNet  MATH  Google Scholar 

  106. Berry D W, Childs A M, Cleve R, et al., Simulating Hamiltonian dynamics with a truncated Taylor series, Phys. Rev. Lett., 2015, 114: 090502.

    Article  Google Scholar 

  107. Berry D W, Childs A M, and Kothari R, Hamiltonian simulation with nearly optimal dependence on all parameters, Proc. FOCS 2015, IEEE, Berkeley, 2015, 792–809.

    Google Scholar 

  108. Low G H and Chuang I L, Hamiltonian simulation by qubitization, arXiv: 1610.06546v2 [quantph].

  109. Chakraborty S, Gilyén A, and Jeffery S, The power of block-encoded matrix powers: Improved regression techniques via faster Hamiltonian simulation, arXiv: 1804.01973v1 [quant-ph].

  110. Gilyén A, Su Y, Low G H, et al., Quantum singular value transformation and beyond: Exponential improvements for quantum matrix arithmetics, arXiv: 1806.01838 [quant-ph].

  111. Childs A M and Kothari R, Limitations on the simulation of non-sparse Hamiltonians, Quantum Information and Computation, 2010, 10: 669–684.

    MathSciNet  MATH  Google Scholar 

  112. Rebentrost P, Steffens A, and Lloyd S, Quantum singular value decomposition of non-sparse low-rank matrices, Phys. Rev. A, 2018, 97: 012327.

    Article  MathSciNet  Google Scholar 

  113. Kerenidis I and Prakash A, Quantum recommendation system, Proc. ITCSC 2017, Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Dagstuhl Publishing, 2017, 49: 1–21.

    Google Scholar 

  114. Wang C H and Wossnig L, A quantum algorithm for simulating non-sparse Hamiltonians, arXiv: 1803.08273v1 [quant-ph].

  115. Childs A M, Kothari R, and Somma R D, Quantum algorithm for systems of linear equations with exponentially improved dependence on precision, SIAM J. Comput., 2017, 46: 1920–1950.

    Article  MathSciNet  MATH  Google Scholar 

  116. Ambainis A, Variable time amplitude amplification and quantum algorithms for linear algebra problems, Proc. STACS 2012, Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Dagstuhl Publishing, 2012, 636–647.

    Google Scholar 

  117. Saad Y, Iterative Methods for Sparse Linear Systems, 2nd edition, Society for Industrial and Applied Mathematics, 2003.

    Book  MATH  Google Scholar 

  118. Clader B D, Jacobs B C, and Sprouse C R, Preconditioned quantum linear system algorithm, Phys. Rev. Lett., 2013, 110: 250504.

    Article  Google Scholar 

  119. Wossnig L, Zhao Z K, and Prakash A, Quantum linear system algorithm for dense matrices, Phys. Rev. Lett., 2018, 120: 050502.

    Article  MathSciNet  Google Scholar 

  120. Chen Y A and Gao X S, Quantum algorithms for Boolean equation solving and quantum algebraic attack on cryptosystems, arXiv: 1712.06239v3 [quant-ph].

  121. Chen Y A, Gao X S, and Yuan C M, Quantum algorithms for optimization and polynomial systems solving over finite fields, arXiv: 1802.03856v2 [quant-ph].

  122. Schuld M and Petruccione F, Supervised Learning with Quantum Computers, Springer, 2018.

    Book  MATH  Google Scholar 

  123. Wittek P, Quantum Machine Learning: What Quantum Computing Mean to Data Mining, Academic Press, 2014.

    MATH  Google Scholar 

  124. Wiebe N, Braun D, and Lloyd S, Quantum algorithm for data fitting, Phys. Rev. Lett., 2012, 109(5): 050505.

    Article  Google Scholar 

  125. Schuld M, Sinayskiy I, and Petruccione F, Prediction by linear regression on a quantum computer, Phys. Rev. A, 2016, 94: 022342.

    Article  Google Scholar 

  126. Wang G M, Quantum algorithm for linear regression, Phy. Rev. A, 2017, 96: 012335.

    Article  MathSciNet  Google Scholar 

  127. Lloyd S, Mohseni M, and Rebentrost P, Quantum algorithms for supervised and unsupervised machine learning, arXiv: 1307.0411v2 [quant-ph].

  128. Lloyd S, Rebentrost P, and Mohseni M, Quantum principal component analysis, Nature Physics, 2014, 10: 631–633.

    Article  Google Scholar 

  129. Rebentrost P, Mohseni M, and Lloyd S, Quantum support vector machine for big data classification, Phys. Rev. Lett., 2014, 113(13): 130503.

    Article  Google Scholar 

  130. Rebentrost P, Bromley T R, Weedbrook C, et al., Quantum recurrent neural network, Phys. Rev. A, 2018, 98: 042308.

    Article  Google Scholar 

  131. Altaisky M V, Quantum neural network, arXiv: quant-ph/0107012v2.

  132. Schuld M, Sinayskiy I, and Petruccione F, The quest for a quantum neural network, Quantum Inf. Process, 2014, 13: 2567–2586.

    Article  MathSciNet  MATH  Google Scholar 

  133. Schuld M, Sinayskiy I, and Petruccione F, Simulating a perceptron on a quantum computer, Phys. Lett. A, 2015, 379: 660–663.

    Article  MATH  Google Scholar 

  134. Wan K H, Dahlsten O, Kristjánsson H, et al., Quantum generalisation of feedforward neural networks, NPJ Quantum Information, 2017, 3(1): 36–43.

    Article  Google Scholar 

  135. Wiebe N, Kapoor A, and Svore K, Quantum perceptron models, Advances in Neural Information Processing Systems, 2016, 29: 3999–4007.

    Google Scholar 

  136. Yamamoto A Y, Sundqvist K M, Li P, et al., Simulation of a multidimensional input quantum perceptron, Quantum Inf. Process, 2018, 17(6): 128–139.

    Article  MathSciNet  MATH  Google Scholar 

  137. Schützhold R, Pattern recognition on a quantum computer, Phys. Rev. A, 2003, 67: 062311.

    Article  Google Scholar 

  138. Trugenberger C A, Quantum pattern recognition, Quantum Inf. Process, 2002, 1(6): 471–493.

    Article  MathSciNet  Google Scholar 

  139. Ventura D and Martinez T, Quantum associative memory, Information Sciences, 2000, 124(1): 273–296.

    Article  MathSciNet  Google Scholar 

  140. Low G H, Yoder T J, and Chuang I L, Quantum inference on Bayesian networks, Phys. Rev. A, 2014, 89: 062315.

    Article  Google Scholar 

  141. Sentís G, Calsamiglia J, Muñoz-Tapia R, et al., Quantum learning without quantum memory, Scientific Reports, 2012, 2(708): 1–8.

    Google Scholar 

  142. Barry J, Barry D T, and Aaronson S, Quantum POMDPs, Phys. Rev. A, 2014, 90: 032311.

    Article  Google Scholar 

  143. Clark L A, Huang W, Barlow T M, et al., Hidden quantum Markov models and open quantum systems with instantaneous feedback, Interdisciplinary Symposium on Complex Systems, Eds. by Sanayei A, et al., ECC 14, Springer, Cham, 2015, 143–151.

    Google Scholar 

  144. Adachi S H and Henderson M P, Application of quantum annealing to training of deep neural networks, arXiv: 1510.06356 [quant-ph].

  145. Wiebe N, Kapoor A, and Svore K, Quantum deep learning, arXiv: 1412.3489 [quant-ph].

  146. Amin M H, Andriyash E, Rolfe J, et al., Quantum Boltzmann machine, Phys. Rev. X, 2018, 8: 021050.

    Google Scholar 

  147. Crawford D, Levit A, Ghadermarzy N, et al., Reinforcement learning using quantum Boltzmann machines, arXiv: 1612.05695 [quant-ph].

  148. Kieferova M and Wiebe N, Tomography and generative data modeling via quantum Boltzmann training, Phys. Rev. A, 2017, 96: 062327.

    Article  Google Scholar 

  149. Messiah A, Quantum Mechanics, Vol. II. Wiley, New Jersey, 1976.

    MATH  Google Scholar 

  150. Farhi E, Goldstone J, Gutmann S, et al., Quantum computation by adiabatic evolution, arXiv: quant-ph/0001106v1.

  151. Childs A M, Farhi E, and Preskill J, Robustness of adiabatic quantum computation, Phys. Rev. A, 2001, 65: 012322.

    Article  Google Scholar 

  152. Roland J and Cerf N, Quantum search by local adiabatic evolution, Phys. Rev. A, 2002, 65: 042308.

    Article  Google Scholar 

  153. Aharonov D, van Dam W, Kempe J, et al., Adiabatic quantum computation is equivalent to standard quantum computation, SIAM J. Comput., 2007, 37(1): 166–194.

    Article  MathSciNet  MATH  Google Scholar 

  154. Childs A M, Farhi E, Goldstone J, et al., Finding cliques by quantum adiabatic evolution, Quantum Information and Computation, 2002, 2(181): 181–191.

    MathSciNet  MATH  Google Scholar 

  155. Farhi E, Goldstone F, Gutmann S, et al., A quantum adiabatic evolution algorithm applied to instances of an NP-complete problem, Science, 2001, 292(5516): 472–475.

    Article  MathSciNet  MATH  Google Scholar 

  156. Hogg T, Adiabatic quantum computing for random satisfiability problems, Phys. Rev. A, 2003, 67: 022314.

    Article  Google Scholar 

  157. Reichardt B W, The quantum adiabatic optimization algorithm and local minima, Proc. STOC 2004, ACM Press, New York, 2004, 502–510.

    Google Scholar 

  158. van Dam W and Vazirani U V, Limits on quantum adiabatic optimization, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.394.2905&rep=rep1&type=pdf.

  159. Neven H, Denchev V S, Rose E, et al., Training a binary classifier with the quantum adiabatic algorithm, arXiv: 0811.0416 [quant-ph].

  160. Pudenz K L and Lidar D A, Quantum adiabatic machine learning, Quantum Inf. Process, 2013, 12(5): 2027–2070.

    Article  MathSciNet  MATH  Google Scholar 

  161. Gaitan F and Clark L, Ramsey numbers and adiabatic quantum computing, Phys. Rev. Lett., 2012, 108: 010501.

    Article  Google Scholar 

  162. Gaitan F and Clark L, Graph isomorphism and adiabatic quantum computing, Phys. Rev. A, 2014, 89(2): 022342.

    Article  Google Scholar 

  163. Kitaev A Y, Fault-tolerant quantum computation by anyons, Annals of Physics, 2003, 303(1): 2–30.

    Article  MathSciNet  MATH  Google Scholar 

  164. Freedman M H, Kitaev A, Larsen M J, et al., Topological quantum computation, Bull. Amer. Math. Soc., 2003, 40: 31–38.

    Article  MathSciNet  MATH  Google Scholar 

  165. Aharonov D, Jones V, and Landau Z, A polynomial quantum algorithm for approximating the jones polynomial, Proc. STOC 2006, ACM Press, New York, 2006, 427–436.

    Google Scholar 

  166. Aharonov D, Arad I, Eban E, et al., Polynomial quantum algorithms for additive approximations of the potts model and other points of the tutte plane, arXiv: quant-ph/0702008.

  167. Wocjan P and Yard J, The Jones polynomial: Quantum algorithms and applications in quantum complexity theory, Quantum Information and Computation, 2008, 8(1): 147–180.

    MathSciNet  MATH  Google Scholar 

  168. Arad I and Landau Z, Quantum computation and the evaluation of tensor networks, SIAM J. Comput., 2010, 39(7): 3089–3121.

    Article  MathSciNet  MATH  Google Scholar 

  169. Aaronson S, The limits of quantum computers, Scientific American, 2008, 298(3): 62–69.

    Article  Google Scholar 

  170. Aaronson S, BQP and the polynomial hierarchy, Proc. STOC 2010, ACM Press, New York, 2010, 141–150.

    Google Scholar 

  171. Mahadev U, Classical Verification of Quantum Computations, arXiv: 1804.01082v2 [quant-ph].

  172. Cirac J and Zoller P, Quantum computation with cold trapped ions, Phys. Rev. Lett., 1995, 74: 4091–4094.

    Article  Google Scholar 

  173. Gershenfeld N and Chuang I L, Bulk spin resonance quantum computing, Science, 1997, 275: 350–356.

    Article  MathSciNet  MATH  Google Scholar 

  174. Loss D and Di Vincenzo D, Quantum computation with quantum dots, Phys. Rev. A, 1998, 57: 120–126.

    Article  Google Scholar 

  175. Vandersypen L M K, Steffen M, Breyta G, et al., Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance, Nature, 2001, 414(6866): 883–887.

    Article  Google Scholar 

  176. Zhao Z, Chen Y A, Zhang A N, et al., Experimental demonstration of five-photon entanglement and open-destination teleportation, Nature, 2004, 430(6995): 54–58.

    Article  Google Scholar 

  177. 12-qubits reached in quantum information quest, https://www.sciencedaily.com/releases/2006/05/060508164700.htm.

  178. World’s First 28 qubit Quantum Computer Demonstrated Online at Supercomputing 2007 Conference, https://www.nanowerk.com/news/newsid=3274.php.

  179. Dwave System’s 128 qubit chip has been made, https://www.nextbigfuture.com/2008/12/dwavesystems-128-qubit-chip-has-been.html.

  180. Monz T, Schindler P, Barreiro J T, et al., 14-Qubit Entanglement: Creation and Coherence, Phys. Rev. Lett., 2011, 106(13): 130506.

    Article  Google Scholar 

  181. D-wave systems breaks the 1000 qubit quantum computing barrier, https://www.dwavesys.com/press-releases/d-wave-systems-breaks-1000-qubit-quantum-computing-barrier.

  182. O’Malley P J J, Babbush R, Kivlichan I D, et al., Scalable quantum simulation of molecular energies, Phys. Rev. X, 2016, 6: 031007.

    Google Scholar 

  183. IBM just made a 17 qubit quantum processor, its most powerful one yet, https://motherboard.vice.com/enus/article/wnwk5w/ibm-17-qubit-quantum-processor-computer-google.

  184. Quantum inside: Intel manufactures an exotic new chip, https://www.technologyreview.com/s/609094/quantum-inside-intel-manufactures-an-exotic-new-chip/.

  185. IBM Q Experience, https://quantumexperience.ng.bluemix.net/qx/experience.

  186. Coles P J, Eidenbenz S, Pakin S, et al., Quantum Algorithm Implementations for Beginners, arXiv: 1804.03719v1 [cs.ET].

  187. China builds five qubit quantum computer sampling and will scale to 20 qubits by end of this year and could any beat regular computer next year, https://www.nextbigfuture.com/2017/05/chinabuilds-ten-qubit-quantum-computer-and-will-scale-to-20-qubits-by-end-of-this-year-and-couldany-beat-regular-computer-next-year.html.

  188. IBM raises the bar with a 50-qubit quantum computer, https://www.technologyreview.com/s/609451/ibm-raises-the-bar-with-a-50-qubit-quantum-computer/.

  189. D-wave announces d-wave 2000q quantum computer and first system order, https://www.dwavesys.com/press-releases/d-wave-announces-d-wave-2000q-quantum-computer-and-first-system-order.

  190. CES 2018: Intel’s 49-qubit chip shoots for quantum supremacy, https://spectrum.ieee.org/techtalk/computing/hardware/intels-49qubit-chip-aims-for-quantum-supremacy.

  191. Google moves toward quantum supremacy with 72-qubit computer, https://www.sciencenews.org/article/google-moves-toward-quantum-supremacy-72-qubit-computer.

  192. Lu C Y, Browne D E, and Yang T, Demonstration of a compiled version of Shor’s quantum factoring algorithm Using Photonic Qubits, Phys. Rev. Lett., 2007, 99: 250504.

    Article  Google Scholar 

  193. Lanyon B P, Weinhold T J, Langford N K, et al., Experimental demonstration of a compiled version of Shor’s algorithm with quantum entanglement, Phys. Rev. Lett., 2007, 99(25): 250505.

    Article  Google Scholar 

  194. Martin-Lopez E, Laing A, Lawson T, et al., Experimental realisation of Shor’s quantum factoring algorithm using qubit recycling, Nat. Photon., 2012, 6: 773–776.

    Article  Google Scholar 

  195. Chuang I L, Gershenfeld N, and Kubinec M, Experimental implementation of fast quantum searching, Phys. Rev. Lett., 1998, 80: 3408–3411.

    Article  Google Scholar 

  196. Vandersypen L M K, Steffen M, Sherwood M H, et al., Implementation of a three-quantum-bit search algorithm, Appl. Phys. Lett., 2000, 76: 646–648.

    Article  Google Scholar 

  197. Barz S, Kassal I, and Ringbauer M, Solving systems of linear equations on a quantum computer, Sci. Rep., 2014, 4: 115.

    Google Scholar 

  198. Cai X D, Weedbrook C, Su Z E, et al., Experimental quantum computing to solve systems of linear equations, Phys. Rev. Lett., 2013, 110(23): 230501.

    Article  Google Scholar 

  199. Pan J W, Cao Y D, Yao X W, et al., Experimental realization of quantum algorithm for solving linear systems of equations, Phys. Rev. A, 2014, 89: 022313.

    Article  Google Scholar 

  200. Ambainis A, New Developments in Quantum Algorithms, Mathematical Foundations of Computer Science, Eds. by Hlineny P, et al., LNCS 6281, Springer, Berlin, Heidelberg, 2010, 1–11.

    Google Scholar 

  201. Cleve R, Ekert A, Macchiavello C, et al., Quantum algorithms revisited, Proc. R. Soc. A, 1997, 454(1969): 339–354.

    Article  MathSciNet  MATH  Google Scholar 

  202. Montanaro A, Quantum algorithms: An overview, npj Quantum Information, 2016, 2: 15023.

    Article  Google Scholar 

  203. Shor P W, Progress in quantum algorithms, Quantum Inf. Process, 2004, 3: 5–13.

    Article  MathSciNet  MATH  Google Scholar 

  204. Sun X M, A survey on quantum computing, Sci. China Inf. Sci., 2016, 8: 982–1002 (in Chinese).

    Google Scholar 

  205. Dervovic D, Herbster M, Mountney P, et al., Quantum linear systems algorithms: A primer, arXiv: 1802.08227v1 [quant-ph].

  206. Kaye P, Laflamme R, and Mosca M, An Introduction to Quantum Computing, Oxford University Press, New York, 2007.

    MATH  Google Scholar 

  207. Rieffel E and Polak W, Quantum Computing — A Gentle Introduction, The MIT Press, Cambridge, Massachusetts London, England, 2011.

    MATH  Google Scholar 

  208. Ambainis A, Quantum walks and their algorithmic applications, International Journal of Quantum Information, 2003, 1: 507–518.

    Article  MATH  Google Scholar 

  209. Elías S, Venegas-Andraca S E, Quantum walks: A comprehensive review, Quantum Inf. Process, 2012, 11(5): 1015–1106.

    Article  MathSciNet  MATH  Google Scholar 

  210. Nayak A, Richter P C, and Szegedy M, Quantum analogs of markov chains, Encyclopedia of Algorithms, Ed. by Kao M Y, Springer, Berlin, Heidelberg, 2014, 1–10.

    Google Scholar 

  211. Santha M, Quantum walk based search algorithms, Proc. TAMC 2008, Xi’an, 2008, 31–46.

    Google Scholar 

  212. Kempe J, Quantum random walks - an introductory overview, Contemporary Physics, 2003, 44(4): 307–327.

    Article  Google Scholar 

  213. Childs A M, Maslov D, Nam Y, et al., Toward the first quantum simulation with quantum speedup, Proceedings of the National Academy of Sciences, 2018, 115: 9456–9461.

    Article  MathSciNet  Google Scholar 

  214. Adcock J C, Allen E, Day M, et al., Advances in quantum machine learning, arXiv: 1512.02900v1 [quant-ph].

  215. Arunachalam S and de Wolf R, A Survey of Quantum Learning Theory, arXiv:1701.06806v3[quant-ph].

  216. Biamonte J, Wittek P, Pancotti N, et al., Quantum machine learning, Nature, 2017, 549: 195–202.

    Article  Google Scholar 

  217. Ciliberto C, Herbster M, Ialongo A D, et al., Quantum machine learning: A classical perspective, Proc. R. Soc. A, 2018, 474(2209): 20170551.

    Article  MathSciNet  MATH  Google Scholar 

  218. Dunjko V and Briegel H J, Machine learning & artificial intelligence in the quantum domain, arXiv: 1709.02779v1 [quant-ph].

  219. Schuld M, Sinayskiy I, and Petruccione F, An introduction to quantum machine learning, Contemporary Physics, 2015, 56(2): 172–185.

    Article  MATH  Google Scholar 

  220. Albash T and Lidar D A, Adiabatic quantum computing, Rev. Mod. Phys., 2018, 90: 015002.

    Article  Google Scholar 

  221. Quantum algorithm zoo, https://math.nist.gov/quantum/zoo/.

  222. Childs A M, Lecture notes on quantum algorithms, http://www.cs.umd.edu/amchilds/qa/.

  223. Christopher M D and Nielsen A, The Solovay-Kitaev algorithm, Quantum Information and Computation, 2006, 6(1): 81–95.

    MathSciNet  MATH  Google Scholar 

  224. Abrams D S and Lloyd S, Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors, Phys. Rev. Lett., 1999, 83(24): 5162–5165.

    Article  Google Scholar 

  225. Buhrman H, Cleve R, Watrous J, et al., Quantum fingerprinting, Phys. Rev. Lett., 2001, 87(16): 167902.

    Article  Google Scholar 

  226. Long G L, General quantum interference principle and duality computer, Common. Theor. Phys., 2006, 45: 825–844.

    Article  MathSciNet  Google Scholar 

  227. Childs A M and Wiebe N, Hamiltonian simulation using linear combinations of unitary operations, Quantum Information and Computation, 2012, 12: 901–924.

    MathSciNet  MATH  Google Scholar 

  228. Kerenidis I and Prakash A, Quantum gradient descent for linear systems and least squares, arXiv: 1704.04992v3 [quant-ph].

  229. Rebentrost P, Schuld M, Wossnig L, et al., Quantum gradient descent and Newton’s method for constrained polynomial optimization, arXiv: 1612.01789v2 [quant-ph].

  230. Grover L K and Rudolph T, Creating superpositions that correspond to efficiently integrable probability distributions, arXiv: quant-ph/0208112.

  231. Soklakov A N and Schack R, Efficient state preparation for a register of quantum bits, Phys. Rev. A, 2006, 73: 012307.

    Article  Google Scholar 

  232. Alpaydin E, Introduction to Machine Learning, 3rd Edition, The MIT Press, Massachusetts, 2015.

    MATH  Google Scholar 

  233. Mackay D, Information Theory, Inference and Learning Algorithms, Cambridge University Press, Cambridge, 2003.

    MATH  Google Scholar 

  234. Sra S, Nowozin S, and Wright S J, Optimization for Machine Learning, The MIT Press, Massachusetts, 2011.

    Book  Google Scholar 

  235. Golub G H and Van Loan C F, Matrix Computations, 4th Edition, The John Hopkins University Press, Baltimore, MD, 2013.

    MATH  Google Scholar 

  236. Hestenes M R and Stiefel E, Methods of conjugate gradients for solving linear systems, J. Res. Natl. Bur. Stand., 1952, 49: 409–436.

    Article  MathSciNet  MATH  Google Scholar 

  237. Aaronson S, Quantum Machine Learning Algorithms: Read the Fine Print, Nature Physics, 2015, 11(4): 291–293.

    Article  Google Scholar 

  238. Childs A M, Quantum algorithms: Equation solving by simulation, Nature Physics, 2009, 5(5): 861.

    Article  Google Scholar 

  239. Harrow A W, Quantum algorithms for systems of linear equations, Encyclopedia of Algorithms, Ed. by Kao M Y, Springer, Berlin, Heidelberg, 2016, 1680–1683.

    Chapter  Google Scholar 

  240. Giovannetti V, Lloyd S, and Maccone L, Architectures for a quantum random access memory, Phys. Rev. A, 2008, 78: 052310.

    Article  MATH  Google Scholar 

  241. Giovannetti V, Lloyd S, and Maccone L, Quantum random access memory, Phys. Rev. Lett., 2008, 100: 160501.

    Article  MathSciNet  MATH  Google Scholar 

  242. Kerenidis I and Prakash A, A quantum interior point method for LPs and SDPs, arXiv: 1808.09266v1 [quant-ph].

  243. Bardet M, Faugère J C, Salvy B, et al., On the complexity of solving quadratic boolean systems, Journal of Complexity, 2013, 29(1): 53–75.

    Article  MathSciNet  MATH  Google Scholar 

  244. Hastie T, Tibshirani R, and Friedman J, The Elements of Statistical Learning, Springer, New York, 2001.

    Book  MATH  Google Scholar 

  245. Haykin S, Neural Networks and Learning Machines, 3rd Edition, Pearson, 2009.

    Google Scholar 

  246. Cleveland W S, Robust locally weighted regression and smoothing scatterplots, Journal of the American Statistical Association, 1979, 74(368): 829–836.

    Article  MathSciNet  MATH  Google Scholar 

  247. Cleveland W S and Devlin S J, Locally-weighted regression: An approach to regression analysis by local fitting, Journal of the American Statistical Association, 1988, 83(403): 596–610.

    Article  MATH  Google Scholar 

  248. Ng A, Supervised learning, discriminative algorithms, http://cs229.stanford.edu/notes/cs229-notes1.pdf.

  249. Suykens J A K and Vandewalle J, Least squares support vector machine classifiers, Neural Processing Letters, 1999, 9(3): 293–300.

    Article  Google Scholar 

  250. Levin D A, Peres Y, and Wilmer E L, Markov Chains and Mixing Times, American Mathematical Society, Providence, Rhode Island, 2009.

    Google Scholar 

  251. Lovász L, Random walks on graphs — A survey, Combinatorics, 1993, 1–46.

    MATH  Google Scholar 

  252. Gerschgorin S, Über die Abgrenzung der Eigenwerte einer Matrix, Izv. Akad. Nauk. USSR Otd. Fiz.-Mat. Nauk, 1931, 7: 749–754.

    MATH  Google Scholar 

  253. Høyer P and Komeili M, Efficient quantum walk on the grid with multiple marked elements, STACS 2017, Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Dagstuhl Publishing, 2017, 42:1–42:14.

    Google Scholar 

  254. Watrous J, Quantum simulations of classical random walks and undirected graph connectivity, Journal of Computer and System Sciences, 2001, 62(2): 376–391.

    Article  MathSciNet  MATH  Google Scholar 

  255. Aharonov D, Ambainis A, Kempe J, et al., Quantum walks on graphs, Proc. STOC 2001, ACM Press, New York, 2001, 50–59.

    Google Scholar 

  256. Kendon V, Quantum walks on general graphs, Int. J. Quantum Inf., 2006, 4(5): 791–805.

    Article  MATH  Google Scholar 

  257. Potocek V, Gabris A, Kiss T, et al., Optimized quantum random-walk search algorithms on the hypercube, Phys. Rev. A, 2009, 79: 012325.

    Article  Google Scholar 

  258. Tonchev H, Alternative coins for quantum random walk search optimized for a hypercube, Journal of Quantum Information Science, 2015, 5: 6–15.

    Article  Google Scholar 

  259. Ambainis A, Quantum search with variable times, Theory of Computing Systems, 2010, 47(3): 786–807.

    Article  MathSciNet  MATH  Google Scholar 

  260. Boyer M, Brassard G, Høyer P, et al., Tight bounds on quantum searching, Fortsch. Phys. Prog. Phys., 1998, 46(4–5): 493–505.

    Article  Google Scholar 

  261. Grover L K, Fixed-point quantum search, Phys. Rev. Lett., 2005, 95: 150501.

    Article  MATH  Google Scholar 

  262. Yoder T J, Low G H, Chuang I L, Optimal fixed-point quantum amplitude amplification using Chebyshev polynomials, Phys. Rev. Lett., 2014, 113: 210501.

    Article  Google Scholar 

  263. Brassard G, Høyer P, and Tapp A, Quantum algorithm for the collision problem, ACM SIGACT News, 1997, 28: 14–19.

    Article  Google Scholar 

  264. Falk M, Quantum search on the spatial grid, arXiv: 1303.4127 [quant-ph].

  265. Buhrman H, Dürr C, Heiligman M, et al., Quantum algorithms for element distinctness, SIAM J. Comput., 2005, 34(6): 1324–1330.

    Article  MathSciNet  MATH  Google Scholar 

  266. Belovs A, Learning-graph-based quantum algorithm for k-distinctness, Proc. FOCS 2012, IEEE, New Brunswick, 2012, 207–216.

    Google Scholar 

  267. Jeffery S, Frameworks for quantum algorithms, PhD thesis, University of Waterloo, 2014.

    Google Scholar 

  268. Krovi H, Magniez F, Ozols M, et al., Quantum walks can find a marked element on any graph, Algorithmica, 2016, 74(2): 851–907.

    Article  MathSciNet  MATH  Google Scholar 

  269. Dohotaru C and Høyer P, Controlled quantum amplification, Proc. ICALP 2017, Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Dagstuhl Publishing, 2017, 18: 1–13.

    Google Scholar 

  270. Ambainis A and Kokainis M, Analysis of the extended hitting time and its properties, Proc. QIP 2015, Philadelphia, 2012.

    Google Scholar 

  271. Portugal R, Santos R A M, Fernandes T D, et al., The staggered quantum walk model, Quantum Information Processing, 2016, 15: 85–101.

    Article  MathSciNet  MATH  Google Scholar 

  272. Aggarwal D, Dadush D, and Regev O, et al., Solving the shortest vector problem in 2n time via discrete Gaussian sampling, Proc. STOC 2014, ACM Press, New York, 2014, 733–742.

    Google Scholar 

  273. Chen Y, Chung K, and Lai C, Space-efficient classical and quantum algorithms for the shortest vector problem, Quantum Information and Computation, 2018, 18(3 & 4): 285–307.

    MathSciNet  Google Scholar 

  274. Becker A, Ducas L, and Gama N, et al., New directions in nearest neighbor searching with applications to lattice sieving, Proc. SODA 2016, SIAM, Philadelphia, 2016, 10–24.

    Google Scholar 

  275. Laarhoven T, Search problems in cryptography, PhD dissertation, Eindhoven University of Technology, Eindhoven, 2015.

    MATH  Google Scholar 

  276. Ettinger M and Høyer P, On quantum algorithms for noncommutative hidden subgroups, Advances in Applied Mathematics, 2000, 25(3): 239–251.

    Article  MathSciNet  MATH  Google Scholar 

  277. Bacon D, Childs A M, and van Dam W, Optimal measurements for the dihedral hidden subgroup problem, Chicago Journal of Theoretical Computer Science, 2006, article 2.

    Google Scholar 

  278. Regev O, A subexponential time algorithm for the dihedral hidden subgroup problem with polynomial space, arXiv: quant-ph/0406151.

  279. Babai L, On the complexity of canonical labeling of strongly regular graphs, SIAM J. Comput., 1980, 9: 212–216.

    Article  MathSciNet  MATH  Google Scholar 

  280. Spielman D A, Faster isomorphism testing of strongly regular graphs, Proc. STOC 1996, ACM Press, New York, 576–584.

  281. Wang F, The Hidden Subgroup Problem, Master’s Project, Aarhus Universitet, 2010.

    Google Scholar 

  282. Ettinger M and Høyer P, A quantum observable for the graph isomorphism problem, arXiv: quant-ph/9901029.

  283. Beals R, Quantum computation of Fourier transforms over symmetric groups, Proc. STOC 1997, ACM Press, New York, 1997, 48–53.

    Google Scholar 

  284. Boneh D and Lipton R J, Quantum cryptanalysis of hidden linear functions, Advances in Cryptology CRYPTO’95, Ed. by Coppersmith D, LNCS 963, Springer-Verlag Berlin, Heidelberg, 1995, 424–437.

    Google Scholar 

  285. Hallgren S, Moore C, Roetteler M, et al., Limitations of quantum coset states for graph isomorphism, J. ACM, 2010, 57(6): 1–33.

    Article  MathSciNet  Google Scholar 

  286. Moore C, Russell A, and Schulman L J, The symmetric group defies strong fourier sampling, SIAM J. Comput., 2008, 37(6): 1842–1864.

    Article  MathSciNet  MATH  Google Scholar 

  287. Kawano Y and Sekigawa H, Quantum fourier transform over symmetric groups, Proc. ISSAC 2013, ACM Press, New York, 2013, 227–234.

    Google Scholar 

  288. Kawano Y and Sekigawa H, Quantum Fourier transform over symmetric groups - improved result, J. Symb. Comp., 2016, 75: 219–243.

    Article  MathSciNet  MATH  Google Scholar 

  289. Williams V V and Williams R, Subcubic equivalences between path, matrix and triangle problems, Proc. FOCS 2010, IEEE, Las Vegas, 2010, 645–654.

    Google Scholar 

  290. Williams V V and Williams R, Finding, minimizing, and counting weighted subgraphs, SIAM J. Comput., 2013, 42(3): 831–854.

    Article  MathSciNet  MATH  Google Scholar 

  291. Williams R, A new algorithm for optimal 2-constraint satisfaction and its implications, Theor. Comput. Sci., 348(2–3): 357–365.

  292. Belovs A, Span programs for functions with constant-sized 1-certificates, Proc. STOC 2012, ACM Press, New York, 2012, 77–84.

    Google Scholar 

  293. Grötschel M, Lovász L, and Schrijver A, Geometric Algorithms and Combinatorial Optimization, Springer, New York, 1988.

    Book  MATH  Google Scholar 

  294. Lee Y T, Sidford A, and Wong S C, A faster cutting plane method and its implications for combinatorial and convex optimization, Proc. FOCS 2015, IEEE, Berkeley, 2015, 1049–1065.

    Google Scholar 

  295. Brandão F G S L and Svore K M, Quantum speed-ups for solving semidefinite programs, Proc. FOCS 2017, IEEE, Berkeley, 2017, 415–426.

    Google Scholar 

  296. Apeldoorn J van, Gilyén A, Gribling S, et al., Quantum SDP-solvers: Better upper and lower bounds, Proc. FOCS 2017, IEEE, Berkeley, 2017, 403–414.

    Google Scholar 

  297. Apeldoorn J van and Gilyén A, Improvements in quantum SDP-solving with applications, arXiv: 1804.05058 [quant-ph].

  298. Brandão F G S L, Kalev A, Li T Y, et al., Quantum SDP solvers: Large speed-ups, optimality, and applications to quantum learning, arXiv: 1710.02581v2 [quant-ph].

  299. Lee Y T, Sidford A, and Vempala S S, Efficient convex optimization with membership oracles, arXiv: 1706.07357 [cs.DS].

  300. Chakraborty S, Childs A M, Li T Y, et al., Quantum algorithms and lower bounds for convex optimization, arXiv: 1809.01731 [quant-ph].

  301. Apeldoorn J van, Gilyén A, Gribling S, et al., Convex optimization using quantum oracles, arXiv: 1809.00643v1 [quant-ph].

  302. Grassl M, Langenberg B, and Roetteler M, et al., Applying Grover’s Algorithm to AES: Quantum Resource Estimates, PQCrypto 2016, Ed. by Takagi T, LNCS 9606, Springer, Cham 2016, 29–43.

    Google Scholar 

  303. Amy M, Di Matteo O, and Gheorghiu V, et al., Estimating the cost of generic quantum pre-image attacks on SHA-2 and SHA-3, Selected Areas in Cryptography, Eds. by Avanzi R and Heys H, LNCS 10532, Springer, Cham, 2017, 317–337.

    Google Scholar 

  304. Dunjko V, Ge Y M, and Cirac I, Computational speedups using small quantum devices, arXiv: 1807.08970 [quant-ph].

  305. Schuld M, Bocharov A, Svore K, et al., Circuit-centric quantum classifiers, arXiv: 1804.00633 [quant-ph].

Download references

Author information

Authors and Affiliations

  1. Academy of Mathematics and Systems Science, University of Chinese Academy of Sciences, Chinese Academy of Sciences, Beijing, 100190, China

    Changpeng Shao, Yang Li & Hongbo Li

Authors
  1. Changpeng Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongbo Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hongbo Li.

Additional information

This research was supported partially by the National Natural Science Foundation of China under Grant No. 11671388, CAS Project QYZDJ-SSW-SYS022, and GF S&T Innovation Special Zone Project.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shao, C., Li, Y. & Li, H. Quantum Algorithm Design: Techniques and Applications. J Syst Sci Complex 32, 375–452 (2019). https://doi.org/10.1007/s11424-019-9008-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-019-9008-0

Keywords

Search

Navigation