1 Introduction

Mutchler and Young (1975) suggested that flows conveyed into rills can transport more than 80% of the soil loss originated from interrill areas and delivered to rills (Bagarello and Ferro 2004; Govers et al. 2007; Bruno et al. 2008; Bagarello and Ferro 2010; Di Stefano et al. 2013, 2015; Bagarello et al. 2015; Peng et al. 2015; Zhang et al. 2016). The basic concepts of particle detachment and transport capacity of a flow also apply to rill areas in which runoff and sediment delivered from interrill areas are combined with erosion and transport processes by rill flows (Toy et al. 2002; Govers et al. 2007).

Flow resistance is affected by the interaction between flow and a mobile rill channel whose geometry varies with the flow shaping action and the joined sediment load. The result of the flow shaping action can be a flat bed, whose roughness is simply represented by a characteristic bed particle diameter, or bed forms constituted of deposited sediments (Di Stefano et al. 2017a, b).

Although there is a considerable body of knowledge describing the effect of flow velocity and turbulence on the initial motion and transport of bed particles, there is a lack of information concerning the feedback effect of bed-load transport on flow characteristics (Naden 1988; Bergeron and Carbonneau 1999; Recking et al. 2008a; Hosseini and Hajibabaei 2020).

Previous studies of bed-load transport resistance in rough open-channel flows (Chow 1959; Vanoni and Nomicos 1960; Baiamonte and Ferro 1997; Song et al. 1998; Gao and Abrahams 2004; Campbell et al. 2005; Recking et al. 2008b; Wang et al. 2011; Ferro 2018a) stated that the sediment load produces a flow resistance increase compared to a clear flow. These studies also demonstrated that when sediments are injected into a clear flow, the resistance increases with the amount of added sediments up to the actual sediment load G is close to the flow transport capacity Tc (Gao and Abrahams 2004). In this equilibrium condition (G = Tc), Gao and Abrahams (2004) highlighted that the Darcy-Weisbach friction factor corresponding to the bed-load transport resistance increases with sediment concentration.

When the actual sediment load G is lower than the flow transport capacity Tc, the rill flow is able to scour the wetted perimeter in order to reduce the difference (Tc – G) for reaching an equilibrium condition. In this non-equilibrium condition for the sediment transport (G < Tc), the induced erosion-transport phenomena affect the flow resistance.

The flow resistance mechanism is supported by the idea that a fraction of flow momentum is used for bed-load transport of particles and that this momentum extraction produces flow velocity reduction (Ferro 2018a). This velocity reduction causes an increase in the apparent roughness length (bed-load roughness). According to Bergeron and Carbonneau (1999), this additional roughness is produced “by the wakes that are shed from individual bed-load grains as they are accelerated by the flow” and its magnitude depends on the bed-load layer thickness and the concentration of bed-load grains (Wiberg and Rubin 1989).

Although the influence of bed-load transport on flow resistance mechanisms was largely experimentally examined (Ferro 2018b), the effect of the sediment transport on flow resistance remains a subject to develop. Chow (1959) suggested that eddies, generated from the boundary surface, are responsible for the transport of sediment particles and this movement interacts and modifies the eddy generation and the flow velocity at channel bed.

Gao and Abrahams (2004) hypothesized that the transfer of flow momentum from the flow to the bed particle occurs in a two-step process: (1) a fraction of the flow momentum is transferred to bed particles which are lifted and accelerated; (2) a loss of flow momentum occurs when particles impact with the bed or collide with particles moving into the flow. This loss of momentum produces a flow velocity decrease and a flow resistance increase and this last effect is named bed-load transport resistance (Gao and Abrahams 2004).

When bed-load transport occurs, the particle movement increases flow resistance (Song et al. 1998) as sediment transport is affected by inter-particle collision. In particular, the frequency of particle collision, which is associated with the increase of bed-load transport, should intensify the flow energy loss. Vanoni and Nomicos (1960) highlighted that the bed-load transport of particles determines changes in bed configuration and affects the friction factor producing an increase of flow resistance greater than that due to the suspended load.

Notwithstanding that many specific resistance equations for rill flows have been proposed (Foster et al. 1984; Line and Meyer 1988; Gilley et al. 1990; Govers 1992; Abrahams et al. 1996; Takken et al. 1998; Hessel et al. 2003; Govers et al. 2007; Di Stefano et al. 2017a), the scientific gap due to the difference between rill flows and the hydraulics of the wide channel has to be yet overcome.

Rill morphology is affected by the interaction among the rill flow characteristics, the erodible wetted perimeter and sediment transport. The shaping action of the rill channel, due to this interaction, limits the applicability of the uniform flow equation developed for large and fixed beds (i.e., Chezy’s and Manning’s equation). Notwithstanding these discrepancies from actual condition, many soil erosion models currently use Chezy’s equation (Ferro 1999; Govers et al. 2007; Powell 2014; Strohmeier et al. 2014; Nouwakpo et al. 2016). The limited availability of rill erosion measurements continues to stimulate researchers to experimentally test the applicability of equations commonly used in rill erosion models (Stroosnijder 2005; Govers et al. 2007; Wirtz et al. 2012).

As is known, the integration of the velocity profile along the cross section allows deducing the flow resistance law (Ferro and Baiamonte 1994). The difficulties of taking into account the variability of the velocity profile among different verticals of a cross section and the unavailability of local velocity measurements justify the scarce attention for the direct relationship between velocity profile and flow resistance law and the widespread use of friction factor values empirically deduced.

The estimate of flow resistance from bulk measurements (slope, water depth, water cross section, discharge) has widely supported the application of an empirical flow resistance equation such as that of Darcy-Weisbach (Ferro 1999; Powell 2014):

$$V= \sqrt{\frac{8 g R s}{f}}$$
(1)

in which V (m s−1) is the cross-section average velocity, f is Darcy-Weisbach friction factor, s (m m−1) is channel slope, R (m) is hydraulic radius, and g (m s−2) is acceleration due to gravity.

Recently, Ferro (2018a) extended the applicability of a theoretical flow resistance law deduced for clear open-channel flow (Ferro 2017, 2018b; Ferro and Porto 2018a,  b) to the condition of equilibrium bed-load transport.

The deduced flow resistance law, which relates the Darcy-Weisbach friction factor to a dimensionless Γ function appearing in the velocity profile (see Eq. 6), was calibrated using flume measurements by Recking et al. (2008a,  b) of bed slope, water depth, and flow velocity. In particular, the analysis developed a relationship between the Γ function, the channel slope, the Shields number, and the Froude number. The proposed flow resistance equation was also tested using field data collected in 104 reaches of some Calabrian gravel bed rivers (Ferro and Porto 2018b).

Di Stefano et al. (2019a) tested the same theoretical flow resistance equation using 35 experimental runs of Jiang et al. (2018) which investigated the effect of flow discharge and slope steepness on rill sediment transport capacity. The analysis confirmed that function can be estimated using the channel slope, the Shields number, and the Froude number and that the flow resistance law allows for an accurate estimate of the friction factor f.

Di Stefano et al. (2019b) carried out a comparison between fixed and mobile bed rills for investigating the component of f, named ft, due to sediment transport, assuming that the former and the component due to grain resistance are additive. The value of ft was negligible for 64% of cases and ≥ 6% of f only for 20% of cases. Di Stefano et al. (2019b) detected the independence of mean flow velocity from channel slope for both mobile and fixed bed rills and explained this result with the occurrence of the feedback mechanism (Govers 1992). In particular, for mobile bed rills, the expected increase of flow velocity due to slope is counterbalanced by the effect of the increase of erosion rate, which produces an increase of bed roughness, with increasing slope. For fixed bed rills, the velocity invariance with slope was justified, taking into account that the implemented experimental procedure was carried out fixing a mobile bed channel shaped by flow at the end of the experimental run. In other words, first Di Stefano et al. (2019b) carried out the measurements on a mobile bed rill which was then fixed for the subsequent runs. Consequently, the roughness of the fixed bed rill was coincident with the “final” roughness of the mobile bed rill, which increased with rill channel slope.

The aim of this paper is testing the applicability of the theoretical flow resistance law deduced by dimensional analysis and self-similarity theory (Di Stefano et al. 2017a; Ferro 2017, 2018a, b; Palmeri et al. 2018) using the rill flow measurements carried out in this investigation and the flume data under equilibrium sediment transport conditions by Jiang et al. (2018). To extend the applicability range of the flow resistance equation, the present measurements were conducted with a soil having a grain-size distribution different from that used by Jiang et al. (2018) and for fixed and mobile bed rills. At the best of our knowledge, the database used in this investigation is relevant as the values of slope steepness, Reynolds number, Froude number, and transport capacity cover a wide range of hydraulic conditions. Although the theoretical flow resistance law has been already tested in previous papers (e.g., Di Stefano et al. 2017a; Palmeri et al. 2018), two novel contributions based on original measurements are released by the present investigation. The first is the evaluation of the effect of sediment transport on rill flow resistance. For this purpose, the f measurements carried out on mobile bed rills and the f values estimated by the flow resistance equation, calibrated by fixed bed rill measurements, are used. This type of analysis was conducted by Di Stefano et al. (2019b) for clay soil and is further extended to a soil with a different texture in the present investigation. The second contribution refers to testing an experimental procedure to obtain fixed bed rills different from that used by Di Stefano et al. (2019b). In particular, for given slope and inflow discharge, the fixed bed runs were performed in rill channels where no preceding mobile bed runs were carried out. The specific objective is to test if the feedback mechanism detected by Di Stefano et al. (2019b) also occurs in fixed bed rills under the experimental procedure applied here.

2 The theoretical rill flow resistance equation

In previous papers, Di Stefano et al. (2017, 2018a, b) underlined that the rill flow resistance equation can be deduced applying the Theorem of the dimensional analysis and self-similarity theory (Barenblatt 1979, 1987, 1993; Ferro 1997, 2017, 2018a ,b; Ferro and Porto 2018a; Palmeri et al. 2018).

The velocity distribution v(y), in which v is the local velocity and y is the distance from the bottom, along a given vertical of a uniform open-channel flow can be expressed in the following dimensionless form (Barenblatt 1987, 1993):

$$\frac{y}{{u}_{*}} \frac{dv}{dy}= {\phi }_{1}\left(\frac{{u}_{*} y}{{\nu }_{k}},\frac{{u}_{*} h}{{\nu }_{k}}, \frac{h}{d},s, F\right)$$
(2)

in which 1 is a functional symbol, h is water depth, d is a characteristic particle diameter, \({u}_{*}= \sqrt{g R s}\) is the shear velocity, is the water density, is the water dynamic viscosity, k is the kinematic viscosity, and \(F= V/\sqrt{g h}\) is the flow Froude number.

Assuming the Incomplete Self-Similarity (ISS) in u*y/k (Barenblatt and Monin 1979; Barenblatt and Prostokishin 1993; Ferro and Pecoraro 2000; Ferro 2017) and integrating Eq. (2), Ferro (2018a) obtained the following power velocity distribution:

$$\frac{v}{{u}_{*}} =\left[{ \frac{1}{\delta } \phi }_{2}\left(\frac{{u}_{*} h}{{\nu }_{k}}, \frac{h}{d},s, F\right)\right]{\left(\frac{{u}_{*}y}{{\nu }_{k}}\right)}^{\delta }+{C}_{i}$$
(3)

in which 2 is a functional symbol, is an exponent, and Ci is an integration constant.

Taking into account that Ci can be assumed equal to 0 (Butera et al. 1993; Barenblatt and Protokishin 1993; Ferro and Pecoraro 2000), the ratio between u*h/k and h/d is equal to the shear Reynolds number Re*, and F accounts for both the depth sediment ratio h/d and Re* (Ferro 2018b), Eq. (3) can be expressed in the following form:

$$\frac{v}{{u}_{*}} =\Gamma \left(s, F\right){\left(\frac{{u}_{*}y}{{\nu }_{k}}\right)}^{\delta }$$
(4)

in which is a function to be defined by velocity measurements and can be calculated by the following theoretical equation (Castaing et al. 1990; Barenblatt 1991):

$$\delta = \frac{1.5}{\mathrm{ln}Re}$$
(5)

in which Re = V h/k is the flow Reynolds number.

The integration of Eq. (4) allows us to obtain the following expression of the Darcy-Weisbach friction factor f (Barenblatt 1993; Ferro 2017; Ferro and Porto 2018a):

$$f=8 {\left[\frac{{2}^{1-\delta }\Gamma { Re}^{\delta } }{\left(\delta +1\right) \left(\delta +2\right)}\right]}^{-2/\left(1+\delta \right)}$$
(6)

The following estimate v of is obtained using Eq. (4) (Ferro, 2017; Ferro and Porto 2018a, b) in which y = h is set as the distance from the bottom at which the local velocity is equal to the cross-section average velocity V:

$${\Gamma }_{v}= \frac{V}{{u}_{*} {\left(\frac{{u}_{* }\alpha h}{{\nu }_{k}}\right)}^{\delta }}$$
(7)

where is a coefficient, less than 1. This coefficient takes into account that V is located below the water surface and a mean velocity profile is considered representative of the velocity distribution in the whole cross section. A theoretical equation for calculating the coefficient is available (Ferro 2017) and Di Stefano et al. (2017a) deduced that, for rill flows with Re ranging from 2000 to 10,000, can be assumed constant and equal to 0.124.

Using measurements of flow velocity, water depth, cross-section area, wetted perimeter, and bed slopes carried out in some mobile bed rills shaped on an experimental plot, Di Stefano et al. (2017a) tested the applicability of Eq. (6) and determined the following expression of the v function (Di Stefano et al. 2018b; Palmeri et al. 2018; Ferro 2018b; Ferro and Porto 2018b):

$${\Gamma }_{v}= \frac{a {F}^{b}}{{s}^{c}}$$
(8)

in which a, b, and c are coefficients to be estimated by measurements.

3 Materials and methods

3.1 Experiments carried out in this investigation

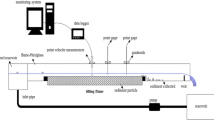
The experimental runs were carried out on a plot (Fig. 1), 2 m wide, 7 m long, located at the experimental area of the Department of Agriculture, Food and Forest Sciences of the University of Palermo. The plot was filled with a soil having a clay percentage of 32.7%, silt of 30.9%, and sand of 36.4%. Two different values of plot slope sp, equal to 9% and 15%, were investigated.

Fig. 1
figure 1

View of the experimental plot

Full size image

Mobile bed rills were manually incised along the plot maximum slope direction and shaped by a clear flow discharge (0.1 L s−1 was applied for 3 min). In particular, the incipient channels excavated by hand were enlarged and deepened by a clear inflow discharge. Then, the experimental runs were carried out on these pre-shaped rills using a constant inflow clear discharge ranging from 0.21 to 0.87 L s−1 for sp = 9% and from 0.19 to 0.87 L s−1 for sp = 15%. When this constant inflow discharge entered the small channel, the flow was able to transport both the soil particles detached in the shaping phase and available to be transported and those detached from the rill wetted perimeter during the run (Regűés et al. 2000; Seeger et al. 2004; Wirtz et al. 2012; Di Stefano et al. 2017c).

Each rill channel was divided into nine longitudinal segments (Fig. 2). Each segment is bounded by two cross sections having a distance of 0.624 m (Fig. 2b). A rill reach is defined as the distance from a given cross section to the rill end (Fig. 2c). For the mobile bed rills, field measurements were carried out in 117 reaches.

Fig. 2
figure 2

Plan view of the experimental plot (a), scheme of the cross sections (b), and examples of rill reaches (c)

Full size image

For establishing the rill channel geometry (Fig. 3), the three-dimensional Digital Terrain Model (3D-DTM) was created by a 3D-photo reconstruction technique using a set of about 70 photographs taken from the plot area by a digital camera. The resolution of the 3D-DTM was set equal to the mean ground sample distance, GSD, which is the actual terrain surface represented into the pixel of the camera sensor and is calculated as pixH/FL, where pix is the pixel size, H is the average object distance, and FL is the focal length. The detail level of the 3D model increases as GSD decreases. For the camera used in this investigation, pix was equal to 0.00173 mm and FL was equal to 3 mm. Using a mean value of H, representative of the different terrain surveys, equal to 1.8 m, a corresponding GSD value equal to 1.04 mm was obtained. The 3D point clouds were characterized by almost constant values of the root mean square error on ground control points with a mean of 2 mm.

Fig. 3
figure 3

View of the three-dimensional digital terrain model of the plot area with some cross sections and the rill thalweg

Full size image

Convergent images useful for the 3D algorithm assured that any part of the measured plot area was part of at least three photographs. Close-range photogrammetry was applied coupling the Structure from Motion (SfM) and MultiView-Stereo (MVS) techniques (Seiz et al. 2006; Javernick et al. 2014; Frankl et al. 2015), and the Agisoft Photoscan Professional software (version 1.1.6, Agisoft, Russia) was used. From the 3D-DTM, the Digital Elevation Models (DEM) at the end of the shaping phase (D1) and at the end of the experimental runs (D2) were obtained. The total eroded rill volume RV was calculated by DEM of difference between D2 and D1 (Fig. 4).

Fig. 4
figure 4

Spatial distribution, as an example for four rill channels, of the scour depth determined during the experimental run, after the initial shaping phase

Full size image

In each experimental run, the water depth was measured by point gauges, located at the rill thalweg with a spacing of 0.624 m (Fig. 5), having a measurement accuracy of ± 1 mm. For each cross section, the wetted perimeter and the cross-section area were determined by coupling the measured water depth with the transverse profile of the cross section extracted by 3D-DTM (Fig. 3) related to the final condition of the channel at the end of the run (Palmeri et al. 2018). The slope steepness of each rill segment was calculated by the rill thalweg extracted by 3D-DTM.

Fig. 5
figure 5

View of the rills after spraying the surface of the channels with a vinylic glue

Full size image

For each rill reach, the water depth h, the hydraulic radius R, and the slope gradient s were calculated by averaging the values measured in the whole reach.

The rill flow velocity was measured by dye-tracing technique (Line and Meyer 1988; Govers 1992; Abrahams et al. 1996) using a methylene blue solution as tracer. The mean flow velocity V was obtained by correcting the measured flow surface velocity Vs by a constant correction factor v equal to 0.8 (Luk and Merz 1992; Li and Abrahams 1997; Zhang et al. 2010; Di Stefano et al. 2018b). This last choice assures the consistency with previous experimental investigations (Di Stefano et al. 2017a, 2018a; Palmeri et al. 2018) and has an almost negligible effect on the estimate performances of the theoretical flow resistance equation (Eq. 6) (Di Stefano et al. 2018b).

Each experimental run with a mobile bed rill was characterized by a known inflow discharge Q. Table 1 lists the water depth h, the slope gradient s, the mean flow velocity V, and measured Darcy-Weisbach friction factor fmb = 8 g R s/V2.

Table 1 Characteristic data of the experimental runs of the present investigation for mobile bed rills
Full size table

Experiments were also carried out for 72 fixed bed rill reaches for each of the two investigated sp values, using a constant inflow discharge ranging from 0.21 to 0.74 L s−1 for sp = 9% and from 0.22 to 0.72 L s−1 for sp = 15%. Firstly, the rills were manually incised along the plot maximum slope direction, shaped by a clear flow discharge (0.1 L s−1 was applied for 3 min), and finally the rill channel surface was fixed by sprinkling on it a mixture of waterproof vinylic glue and water (1:1) until glue infiltration stopped. After the application, the glue was left to dry for 24 h (Fig. 5). This procedure is different from that applied by Di Stefano et al. (2019b) as fixed bed runs were carried out by rill channels in which no mobile bed runs were previously conducted. The measurements were carried out by the same techniques applied for the mobile bed rill experiments.

For each experimental run with a fixed bed rill characterized by a known inflow discharge Q, the measured values of water depth h, slope gradient s, mean flow velocity V, and Darcy-Weisbach friction factor ffb = 8 g R s/V2 are listed in Table 2.

Table 2 Characteristic data of the experimental runs of the present investigation for fixed bed rills
Full size table

3.2 Experiments byJiang et al. (2018)

The 35 experiments by Jiang et al. (2018) are rill flow measurements carried out for the equilibrium bed-load transport condition. The hydraulic variables and Tc values of this experimental investigation cover a wide range of flow condition and slope.

The flume, 0.12 m wide and 4 m long, schematizes a rill having a rectangular cross section with fixed smooth sides and a no-erodible rough bed. This scheme, which is that of a no-erodible rill in which the flow has a sediment load equal to the transport capacity (G = Tc), can be compared with that of mobile bed rills of this investigation as both experiments were characterized by sediment transport.

The experimental runs were carried out on colluvial soil having a gravel (> 2 mm) percentage of 30%, and percentages of sand, silt, and clay equal to 45%, 23%, and 2%, respectively. The hydraulic measurements (discharge, velocity, transport capacity) carried out for seven slope steepness values (18, 27, 36, 47, 58, 70, and 84%) and five different discharges in the range 0.0672–0.528 L s−1 were characterized by a wide range of flow conditions (Reynolds numbers of 639 ≤ Re ≤ 5529 and Froude numbers of 1.57 ≤ F ≤ 8.14). Further details are reported in the paper by Jiang et al. (2018).

4 Results

4.1 Flow resistance in fixed bed rills

The 72 measurements carried out in this investigation for the fixed bed rills (Table 2) were used to calibrate Eq. (8) obtaining:

$${\Gamma }_{v}= 0.4842\frac{ {F}^{1.1299}}{{s}^{0.551}}$$
(9)

This equation is characterized by a coefficient of determination R2 = 0.983 and it is applicable for flow Reynolds numbers of 2266 ≤ Re ≤ 14,330, Froude numbers of 0.86 ≤ F ≤ 3.54, and slope s values ranging from 7.9 to 16.0%.

The comparison between the 72 v values calculated by Eq. (7), with = 0.124, and those calculated by Eq. (9) is shown in Fig. 6.

Fig. 6
figure 6

Comparison between the 72 v values obtained by Eq. (7) with = 0.124 and those calculated by Eq. (9)

Full size image

For a fixed bed rill, substituting Eq. (9) into Eq. (6), the following flow resistance equation is obtained:

$$f=8 {\left[\frac{\left(\delta +1\right) \left(\delta +2\right) }{{2}^{1-\delta } {Re}^{\delta } 0.4842} \frac{{s}^{0.551}}{{F}^{1.1299}}\right]}^{2/\left(1+\delta \right)}$$
(10)

Figure 7 shows the good agreement between the 72 measured friction factor ffb values and those calculated by Eq. (10), which is characterized by a root mean square error (RMSE) equal to 0.0175. The f estimate errors falling within the error bands of ± 20% and ± 10% are equal to 100% and 91.7%, respectively.

Fig. 7
figure 7

Comparison between the 72 measured friction factor ffb values and those calculated by Eq. (10)

Full size image

Taking into account that Re is constant and equal to 4.4817 and using the mean value of of 0.171 as its experimental range (0.157–0.194) is narrow, Eq. (10) reduces to:

$$f=3.9292 \frac{{s}^{0.941}}{{F}^{1.9299}}$$
(11)

4.2 Effect of sediment transport on rill flow resistance

The component ft of the Darcy-Weisbach friction factor due to the sediment transport was calculated by the difference between the fmb value measured on a mobile bed rill, which takes into account both grain resistance and sediment transport (Table 1), and the f value, calculated for the fixed bed condition by Eqs. (5) and (10), which considers only grain resistance. Specifically, the f value was calculated for the same hydraulic (Re, F) and slope (s) conditions as those corresponding to fmb.

The ft value was negligible for 91 out of 117 measurements. Figure 8 shows the cumulative frequency distribution of the ft/fmb ratio.

Fig. 8
figure 8

Cumulative frequency distribution of the ft/fmb ratio

Full size image

Figure 9 shows, as an example for the four rills represented in Fig. 4, the comparison between the applied discharge Q, the corresponding ratio ft/fmb, and the total eroded rill volume RV. Both ft/fmb and RV increase with Q.

Fig. 9
figure 9

Comparison, as an example for four rill channels, between the applied discharge Q, the corresponding ft/fmb ratio, and the total eroded rill volume RV

Full size image

4.3 Flow resistance in mobile bed rills

The data of Jiang et al. (2018), obtained for a fixed bed rill condition and a sediment-laden flow, were coupled with the measurements carried out in this investigation for the mobile bed rills (Table 1). This choice is justified by the fact that both experiments were characterized by sediment transport conditions. Coupling the data obtained in this investigation and those by Jiang et al. (2018) to calibrate Eq. (8), the following equation was obtained:

$${\Gamma }_{v}= 0.4514\frac{ {F}^{0.9999}}{{s}^{0.5935}}$$
(12)

which is characterized by R2 = 0.979 and is applicable for flow Reynolds numbers of 639 ≤ Re ≤ 12,895, Froude numbers of 0.60 ≤ F ≤ 8.14, and slope s values ranging from 5.1 to 84.0%.

The comparison between the 152 values calculated by Eq. (7), with 0.124, and those calculated by Eq. (12) is shown in Fig. 10.

Fig. 10
figure 10

Comparison between the 152 v values obtained by Eq. (7) with = 0.124 and those calculated by Eq. (12)

Full size image

Substituting Eq. (12) into Eq. (6), the following flow resistance equation for a mobile bed rill is obtained:

$$f=8 {\left[\frac{\left(\delta +1\right) \left(\delta +2\right) }{{2}^{1-\delta } {Re}^{\delta } 0.4514} \frac{{s}^{0.5935}}{{F}^{0.9999}}\right]}^{2/\left(1+\delta \right)}$$
(13)

Figure 11 shows the good agreement between the 152 measured friction factor fmb values and those calculated by Eq. (13), which is characterized by RMSE = 0.062. The f estimate errors falling within the error bands of ± 20% and ± 10% f are equal to 94.7% and 78.3%, respectively.

Fig. 11
figure 11

Comparison between the 152 measured friction factor fmb values and those calculated by Eq. (13)

Full size image

Using a constant value of equal to the experimental mean value of 0.177, Eq. (14) reduces to:

$$f=4.5346 \frac{{s}^{1.008}}{{F}^{1.6992}}$$
(14)

5 Discussion

5.1 Flow resistance in fixed bed rills

For fixed bed rills, Eq. (11) shows that the exponent of s (0.941) is close to 1. According to Eq. (1), when the Darcy-Weisbach friction factor is linearly related with s the flow velocity is independent of channel slope. Taking into account that fixed bed runs were performed in channels in which no mobile bed runs were previously carried out, this result was not expected. In fact, in these rills, no adjustment of the cross-section geometry was allowed. For fixed bed rills obtained immobilizing the mobile bed rills at the end of the runs, Di Stefano et al. (2019b) already found that the mean flow velocity is independent of channel slope and explained this result considering that the final roughness of the mobile bed rill coincides with the roughness of the fixed bed rill. Instead, in this study, no mobile bed runs were carried out before fixing the rill bed. Rills were subjected only to a shaping phase with a small flow discharge of 0.1 L s−1. The result that the mean flow velocity was independent of channel slope can be explained by the influence of the initial shaping phase on the fixed bed rill roughness. In particular, during the shaping phase, the increase of flow velocity with plot slope gradient is counterbalanced by the increase of erosion rate and, consequently, of bed roughness. Thus, the roughness of fixed bed rills was determined by the plot slope gradient, affecting the shaping phase. In other words, a feedback mechanism which is associated to the experimental procedure that provides for a shaping phase is “frozen.” These results do not agree with those by Foster et al. (1984), which detected a relationship between rill flow velocity and slope since their experiments were carried out by a fixed bed replica of a rill, having a constant roughness, which was placed on a laboratory sloping flume. This experimental procedure did not allow a feedback mechanism to occur.

5.2 Effect of sediment transport on rill flow resistance

Figure 8 demonstrates that the effect of sediment transport on total flow resistance is negligible (ratio ft/fmb less than 0.001 for 77.8% of the investigated cases) and the ratio ft/fmb is greater than 5% only for 7.7% of the investigated cases. Therefore, for the investigated conditions, the effect of grain resistance on the flow resistance law is dominant compared to that of sediment transport. This result agrees with that of a previous study on mobile bed rills (Di Stefano et al. 2019b) shaped on a plot filled with clay soil. In fact, this previous investigation demonstrated that the contribution of the sediment transport to the total resistance (grain roughness and sediment transport) was greater than or equal to 6% only for 20% of the measured friction factor values.

Figure 9 highlights that when the discharge Q increases the contribution of sediment transport to flow resistance and the eroded rill volume also increase. This result demonstrates that for increasing discharge values the corresponding increase of sediment load, due to rill erosion processes, produces an increase of the head losses due to sediment transport with respect to grain resistance. In other words, the effect of sediment transport on flow resistance depends on flow transport capacity which increases with flow discharge.

In conclusion, the experimental runs pointed out a limited influence of the sediment transport on flow resistance, as the ratio ft/fmb is always less than 20%, and the effect of sediment transport increases with Tc (Gao and Abrahams 2004). Moreover, since the influence of the transport phenomena on flow resistance is limited, then the achievement of an equilibrium condition during the experimental runs can be hypothesized.

5.3 Flow resistance in mobile bed rills

Equation (14) demonstrates that in the investigated mobile bed rills, the Darcy-Weisbach friction factor increases with slope which is a surrogate for the effect of sediment transport. The exponent of slope (1.008) is close to 1, confirming that a negligible influence of slope on rill velocity occurred. This conclusion can be attributed to the effect of the feedback mechanism proposed by Govers (1992). For the mobile bed rills, the experimental runs confirm that the expected increase of flow velocity with slope gradient is counterbalanced by the effect of the increase of bed roughness which is due to the increase of erosion rate.

For a flume having fixed bed and walls with a sediment-laden flow, which is the condition investigated by Jiang et al. (2018), when the flume slope increases, gains of both mean flow velocity and transport capacity are also expected. In this hydraulic condition, the increase of sediment transport requires an increase of flow momentum which is used for the particle transport and this momentum extraction produces flow velocity reduction (Ferro 2018a). In conclusion, an invariance of mean flow velocity with slope occurs.

6 Conclusions

In this paper, the applicability of the flow resistance equation, obtained by integrating a power velocity distribution, was tested using flow measurements carried out in mobile bed rills with sediment transport conditions and fixed bed rills.

In particular, the following steps were applied for developing the analysis: (i) a relationship (Eq. 8) between the function of the velocity profile, the rill slope, and the Froude number was calibrated by measurements carried out on fixed bed rills and introduced in the flow resistance law to obtain Eq. (10); (ii) the component of f due to sediment transport was deduced from the measurements carried out for mobile bed rills and f values calculated by Eq. (10) in the same slope and hydraulic conditions; (iii) Eq. (8) was calibrated using the measurements carried out in the mobile bed rills and the data by Jiang et al. (2018); (iv) the Darcy-Weisbach friction factor values measured for sediment transport conditions were compared with those calculated by the rill flow resistance equation with estimated by Eq. (12).

The analysis of the measurements carried out in fixed bed rills demonstrated that the feedback mechanism detected by Govers (1992) also occurred for this bed condition. In fact, the roughness of fixed bed rills was conditioned by the shaping phase, which determined an increased roughness with plot slope.

The analysis also demonstrated that effect of sediment transport on flow resistance depends on flow transport capacity which increases with flow discharge, and that the contribution of the sediment transport to the total resistance (grain and sediment transport) is always limited. In other words, for the investigated conditions the effect of grain resistance on the flow resistance law is dominant with respect to that of sediment transport.

The proposed theoretical flow resistance law (Eq. 13) allows for an accurate estimate of the Darcy-Weisbach friction factor for rill flows under sediment transport and a wide range of hydraulic conditions.