Introduction

With technological progress and population growth, a rapid rise in global carbon emissions is inevitable. Global carbon dioxide emissions increased by 40% between 2000 and 2019. According to a report (BP 2021) released by the British Petroleum Company, global carbon emissions have maintained continuous growth since 2013, reaching 34.36 billion tons in 2019, a record high. The increase in carbon dioxide in the atmosphere has led to a rise in surface temperatures, which directly leads to the frequent occurrence of extreme weather, such as drought, heat, and glacial melting. These changes have become a great challenge to human development. Reducing non-renewable energy consumption and controlling carbon dioxide emissions have become common goals of all countries worldwide.

In 2020, with the outbreak of COVID-19, all countries in the world suffered an economic blow to varying degrees, and energy consumption and carbon dioxide emissions in all countries changed dramatically compared to levels before the COVID-19 pandemic, attracting the attention of governments and scholars around the world (Wang et al. 2022). China’s carbon emissions reached 9.899 billion tons, with an annual increase of 0.6% (China’s 2013–2020 carbon emissions are shown in Fig. 1). According to the statistics of the International Energy Agency (IEA, Greenhouse Gas Emissions from Energy 2021), in 2020, global carbon emissions mainly came from energy generation and heating, transportation, and manufacturing and construction, accounting for 43%, 26%, and 17%, respectively (Fig. 2(a)). In 2020, the Asia–Pacific region accounted for more than half of global carbon emissions, with a combined 52%, and China accounted for 30.7%, far more than other regions (Fig. 2(b)).

Fig. 1
figure 1

China’'s carbon emissions from 2013 to 2020 (BP, Statistical Review of World Energy, 2019)

Full size image
Fig. 2
figure 2

(a) Composition of global carbon emission sources in 2020; Fig. 2(b) Composition of global carbon emission regions in 2020 (IEA, Greenhouse Gas Emissions from Energy, 2021)

Full size image

China is a developing country; therefore, its economic development still requires considerable coal energy consumption, and its carbon emissions are still growing. As the world’s largest developing country and the largest energy consumer and carbon dioxide emitter, China’s carbon emissions are closely monitored because they have a direct impact on global trends. Therefore, effectively predicting China’s carbon emissions and grasping the trend of carbon emissions in advance to adjust policies and effectively implement corresponding measures is of great significance. This information can provide a reliable basis for China’s energy conservation and emission reduction measures and serve as an important indicator for global carbon dioxide control.

At present, many scholars have studied the prediction methods of carbon dioxide emissions, including machine learning methods, statistical models, dynamic scenario simulation models, and grey prediction models.

Machine learning methods

Based on classical neural network models, such as generalized regression neural network prediction models (Heydari et al. 2019) and least squares support vector machine models (Sun and Liu 2016; Qiao et al. 2020), scholars have introduced optimization algorithms to improve model performance. In terms of the model structure, many scholars have established neural network models that are more suitable for predicting carbon emissions, such as the machine learning method optimized by Adam and proposed by Ashin Nishan and Muhammed Ashiq (2020) and the meta-elastic network established by Nguyen et al. (2021).

Statistical models

Scholars have used the Ridee regression decomposition method (Ma et al. 2019), cumulative Monte Carlo distribution curve (Robati et al. 2019), regression analysis and other methods (Xia et al. 2019; Modise et al. 2021; Boamah et al. 2021) to predict the carbon emissions of different countries or industries and obtained many excellent results.

Dynamic scenario simulation model

Scholars have used dynamic scenario simulation models to analyze the future trend of carbon emissions, for example, by combining such a model with the Monte Carlo simulation method to construct a new dynamic scenario simulation model (Hu and Lv 2020), discussing the dynamic evolution trajectory of China’s building carbon emissions, and then combining this model with specific data to provide effective information for the government (Huo et al. 2021a, b).

The above models have good effects in predicting carbon emissions, but they all have a common problem: the need for large quantities of high-quality data. Machine learning methods usually require large sample sizes to train models before making predictions, and there may be problems of excessive sample fitting or improper parameter setting. Statistical models and scenario simulation models rely heavily on sufficient and effective input data for accurate calculation, which also requires a considerable amount of data to obtain high-quality effective data. However, current carbon dioxide emissions mainly come from fossil fuels. The COVID-19 pandemic is likely to exacerbate changes in the global energy mix, and historical data of carbon dioxide emissions are inconsistent with the current situation. Due to the substantial reduction in reliable data, models requiring a substantial amount of data modeling are no longer applicable. Therefore, models that requires less data to obtain relatively effective results are attractive (Deng 2002).

The grey prediction model was proposed by Deng (2002). This kind of model has a simple structure and strong adaptability. It can better handle parameters and is suitable for systems with small samples and unclear information. Compared with other methods, the advantage of the grey prediction model is that it can produce accurate results for an uncertain system with scarce data. The grey prediction model weakens the randomness of the original data by generating the cumulative sequence of the original data to mine the hidden rules in the data sequence, and finally simulates and predicts the data through the restoration operation (Duan et al. 2020a; Duan and Pang 2021; Wang and Li 2020; Zeng et al. 2020; Yan et al. 2020). It is widely used in the prediction of energy (Duan and Luo 2021; Duan and Luo 2020; Zhao and Wu 2020; Gao et al. 2022a), transportation (Duan et al. 2020b, Bezuglov and Comert 2016), the environment (Mao et al. 2020; Liu et al. 2020), and other industries (Gao et al. 2022b). The grey prediction model also plays an important role in predicting carbon emissions. The following is a description of the grey univariate model, the multivariate model and the combination of the grey prediction model and other models.

Grey univariate prediction model

This kind of model ignores the influence of other related factors and only considers the change trend and characteristics of the only variable. Scholars have directly applied the existing grey univariate and discrete univariate prediction models to predict carbon emissions (Ikram et al. 2021; Qiao et al. 2021) and introduced rolling mechanisms and other methods based on the classical univariate model to optimize the prediction of carbon emissions (Zhou et al. 2021). The grey multivariate prediction model is a relatively grey univariate prediction model that considers more related factors and therefore has good adaptability. Scholars have generalized and optimized the grey multivariate prediction model based on the model structure (Cao et al. 2021), theoretical derivation (Duan et al. 2020a), and sequence optimization (Ye et al. 2021) and effectively applied it to predict carbon emissions.

Grey univariate and multivariate prediction models have certain advantages, while machine learning models have an excellent performance in parameter calculation and optimization. Therefore, scholars have combined the two models to establish a kind of combined model suitable for small sample data with optimized parameters and performance. Hu and Lv (2020) combined the grey model with the optimized vector machine algorithm to simulate the carbon emission transfer network among various industries. Huang et al. (2019) used grey correlation analysis to identify the strongly correlated factors of carbon emissions and then used the long short-term memory (LSTM) method to predict China’s carbon emissions. Zhao et al. (2021) proposed a hybrid prediction model combining an improved grey model and a machine learning model to analyze the long-term trend and short-term fluctuation of carbon emissions. Combining the neural network model on the basis of the grey prediction model can indeed optimize the model performance, and this idea is practical and effective.

The aforementioned grey prediction models have yielded good prediction results, but some limitations exist. First, most carbon emission prediction applications do not consider the background of the carbon emission system; rather, they establish a model and apply it directly, ignoring the importance of background characteristics. Second, carbon dioxide emissions are affected by many factors, such as population, GDP, and the use of energy. Grey univariate forecasting models have certain limitations in such complex systems, and the aforementioned multivariable or combined models basically choose population and GDP as influencing factors. However, energy and other factors also need to be considered to better describe the carbon emission system. Finally, the combination model of the grey prediction model and machine learning generally combines the two models based on the modeling data, and determining how to combine the two models based on the model structure requires further research.

Therefore, starting from the evolutionary dynamic system of carbon emissions, this paper studies the law of carbon emissions and establishes a grey prediction model based on the principle of grey difference information. At the same time, based on the structure of the model, the grey of model the carbon emission dynamic system is established with a neural network by combining the function of the relevant factors of the model with the neural network. The model is applied to predict carbon emissions in Beijing, China, and good results are obtained.

This paper makes the following three contributions:

  1. (1)

    Based on the evolutionary system of carbon emissions, the concepts of the dynamic evolutionary factor, evolutionary coefficient, and critical time point of carbon emissions are introduced, and the nonlinear grey prediction model of the dynamic system of carbon emissions is established by using the principle of grey difference information.

  2. (2)

    To further analyze the external factors of the dynamic system of carbon emissions, the modeling mechanism of the neural network is used to adjust the external factors, and the grey model of the carbon emission dynamic system is established with a neural network based on the structure of the model.

  3. (3)

    The new model is applied to predict carbon emissions, the effectiveness of the model is analyzed based on the number of modeling objects, and the carbon emissions in the next 5 years are predicted by using the most effective case. Then, relevant policy suggestions are proposed based on the trend of the results.

The remainder of this paper proceeds as follows: In the second section, the grey prediction model is first established by the dynamic method, and then, the grey model of the carbon emission dynamic system is established with a neural network by combining the grey prediction model with the neural network modeling mechanism. In the third section, data on Beijing’s carbon emissions are used to conduct an effective analysis, the carbon emissions in the next 5 years are predicted, and relevant suggestions are proposed. The fourth section presents the conclusions.

A carbon emission dynamic system grey model based on a neural network

System evolution is a dynamic process of occurrence, development, mutation, and complex change over time. Research on the evolutionary law of a system can help to better understand, control, and analyze the system and promote the development process of the system. Carbon emissions are related to macroeconomic factors such as the national economy and energy. To effectively predict carbon emissions, the grey prediction model of the carbon emission evolutionary dynamic system is established based on the carbon emission evolutionary system, and the grey model of the carbon emission dynamic system is established with a neural network by combining the modeling mechanism of the neural network with the grey prediction model.

An evolutionary dynamic system model of carbon emissions

The carbon emission system is a dynamic system, and the evolutionary law of carbon emissions can be studied by dynamic methods. By introducing concepts such as the dynamic evolutionary factor of carbon emissions, evolutionary coefficient and critical time point and by using existing data, the dynamic system of carbon emissions can be established (Tian and Jin 2012). Based on the nonlinear influence, the nonlinear dynamic system model can be established while considering the influence of external factors, which enables policymakers to regulate and adjust external influences. external factors, which is convenient for policy to regulate and adjust external influences.

The evolutionary dynamic system model of carbon emissions is as follows:

$$\frac{dM(t)}{dt}={\text{g}}(M(t))+f(t),t\in I$$
(1)

where \(M\left(t\right)\) represents the carbon emission vector at time \(t\); \(\frac{dM\left(t\right)}{dt}\) represents the dynamic evolutionary factor of carbon emissions, that is, the rate of change in carbon emissions over time; \({\text{g}}(M(t))\) is the composition function of \(M\left(t\right)\); and \(f\left(t\right)\) is the function of regulating external factors.

Considering that the change rate \(\frac{dM\left(t\right)}{dt}\) of the carbon emission factor at time \(t\) is proportional to the carbon emission \(M\left(t\right)\) in the economic period, \(\frac{dM\left(t\right)}{dt}\) is proportional to the share of the growth potential of carbon emissions \(1-\frac{M\left(t\right)}{{ck}_{M}}\). The growth potential of carbon emissions is affected by technological progress, emission reduction technologies, and other factors. At the same time, it is also related to external factors that affect carbon emissions, including energy consumption, the external factors of the system, and the regulatory function \(f\left(t\right)\) of regulatory behavior. Thus, the following dynamic system model of the evolution of carbon emissions can be established:

$$\frac{dM(t)}{dt}=rM(t)(1-\frac{M(t)}{c{k}_{M}})+cf(t)$$
(2)

where \(r\) is the carbon emission coefficient of economic period \(I\); \({k}_{M}\) is related to the time interval; \(c\) is the carbon emission evolutionary coefficient; \(M\left(t\right)\) is carbon emissions; \(t\) is time; and \(f\left(t\right)\) is the policy regulation affecting carbon emissions, which can be determined by external factors such as energy consumption and economic status.

From Eq. (2), the following equation can be obtained:

$$\frac{dM\left(t\right)}{dt}=rM\left(t\right)-\frac{{rM}^{2}\left(t\right)}{{ck}_{M}}+cf\left(t\right)$$
(3)

This system is a direct carbon emission system that enables the overall trend of carbon emissions to be analyzed, and \(f\left(t\right)\) is the external regulatory function. Therefore, we let \(r=a,-\frac{r}{{ck}_{M}}=b\), and the control function is \(cf\left(t\right)=f\left({M}_{1}\left(t\right);\omega \right)\). Then, Eq. (3) becomes the following:

$$\frac{dM\left(t\right)}{dt}=aM\left(t\right)+{bM}^{2}\left(t\right)+f\left({M}_{1}\left(t\right);\omega \right)$$
(4)

Carbon emission dynamic system grey model

Set \({M}^{(0)}\) as the original data sequence of carbon emissions:

$${M}^{\left(0\right)}\left(k\right)=\left({m}^{\left(0\right)}\left(1\right),{m}^{\left(0\right)}\left(2\right),\cdots ,{m}^{\left(0\right)}\left(n\right)\right)$$
(5)

\({M}^{\left(1\right)}\) is the 1-AGO sequence of \({M}^{\left(0\right)}\):

$${M}^{\left(1\right)}\left(k\right)=\left({m}^{\left(1\right)}\left(1\right),{m}^{\left(1\right)}\left(2\right),\cdots ,{m}^{\left(1\right)}\left(n\right)\right),$$
(6)

where \({m}^{\left(1\right)}\left(k\right)=\sum\limits_{i=1}^{k}{m}^{\left(0\right)}\left(i\right),k=\mathrm{1,2},\cdots n.{Z}^{\left(1\right)}\) is the adjacent mean-generating sequence of \({M}^{\left(1\right)}\):

$${Z}^{\left(1\right)}\left(k\right)=\left({z}^{\left(1\right)}\left(1\right),{z}^{\left(1\right)}\left(2\right),\cdots ,{z}^{\left(1\right)}\left(n\right)\right)$$
(7)

where \({z}^{\left(1\right)}\left(k\right)=0.5\left({m}^{\left(1\right)}\left(k\right)+{m}^{\left(1\right)}\left(k-1\right)\right),k=\mathrm{2,3},\cdots ,n.\)

Set \({{M}_{j}}^{\left(0\right)}\) as the sequence of the carbon emission control function:

$${{M}_{j}}^{\left(0\right)}\left(k\right)=\left({{m}_{j}}^{\left(0\right)}\left(1\right),{{m}_{j}}^{\left(0\right)}\left(2\right),\cdots ,{{m}_{j}}^{\left(0\right)}\left(n\right)\right)$$
(8)

\({{M}_{j}}^{\left(1\right)}\) is the 1-AGO sequence,

$${{M}_{j}}^{\left(1\right)}\left(k\right)=\left({{m}_{j}}^{\left(1\right)}\left(1\right),{{m}_{j}}^{\left(1\right)}\left(2\right),\cdots ,{{m}_{j}}^{\left(1\right)}\left(n\right)\right),$$
(9)

where \({{m}_{j}}^{\left(1\right)}\left(k\right)=\sum_{i=1}^{k}{{m}_{j}}^{\left(0\right)}\left(i\right),k=\mathrm{1,2},\cdots n.{Z}^{\left(1\right)}\) is the adjacent mean-generating sequence of \({M}^{\left(1\right)}\):

Assuming that the carbon emissions at time \(t\) are \({M}^{\left(0\right)}\left(t\right)\), the total carbon emissions at time \(\left[0,t\right]\) can be expressed as follows:

$${M}^{\left(0\right)}\left(t\right)=\frac{{dM}^{\left(1\right)}\left(t\right)}{dt}$$

Thus, Eq. (4) can be written as follows:

$$\frac{{dM}^{\left(1\right)}\left(t\right)}{dt}={aM}^{\left(1\right)}\left(t\right)+b{\left[{M}^{\left(1\right)}\left(t\right)\right]}^{2}+f\left({{M}_{j}}^{\left(1\right)}\left(t\right);\omega \right)$$
(10)

Consider using the first-order difference form to replace the differential on the left-hand side of Eq. (4). Then, when \(t=k\),

$$\begin{array}{c}\frac{{dM}^{\left(1\right)}\left(t\right)}{dt}{\left|{}_{t=k}\approx \frac{\Delta {M}^{\left(1\right)}\left(t\right)}{\Delta t}\right|}_{t=k}=\frac{{M}^{\left(1\right)}\left(k\right)-{M}^{\left(1\right)}\left(k-1\right)}{k-\left(k-1\right)}={M}^{\left(1\right)}\left(k\right)-{M}^{\left(1\right)}\left(k-1\right)={M}^{\left(0\right)}\left(k\right);\\ {\int }_{k-1}^{k}{M}^{\left(1\right)}\left(t\right)=\frac{1}{2}\left({M}^{\left(1\right)}\left(k-1\right)+{M}^{\left(1\right)}\left(k-1\right)\right)={Z}^{\left(1\right)}\left(k\right);\\ {\int }_{k-1}^{k}f\left({{M}_{j}}^{\left(1\right)}\left(t\right);\omega \right)=\frac{1}{2}\left(f({{M}_{j}}^{\left(1\right)}\left(k\right);\varpi )+f({{M}_{j}}^{\left(1\right)}\left(k-1\right);\varpi )\right)\end{array}$$

where \({M}^{\left(0\right)}\left(k\right)\) can be regarded as the grey derivative sequence of \({M}^{\left(1\right)}\left(t\right)\) at time \(\left[k-1,k\right]\). Therefore, the grey prediction model is defined as follows:

Definition 1

Let \({M}^{\left(0\right)},{M}^{\left(1\right)},{Z}^{\left(1\right)}\) as shown in the definition of Eqs. (5)–(7). Then,

$${M}^{\left(0\right)}\left(k\right)={aZ}^{\left(1\right)}\left(k\right)+b{\left[{Z}^{\left(1\right)}\left(k\right)\right]}^{2}+\frac{1}{2}\left(f({{M}_{j}}^{\left(1\right)}\left(k\right);\varpi )+f({{M}_{j}}^{\left(1\right)}\left(k-1\right);\varpi )\right)$$
(11)

This is called the carbon emission dynamic system grey model (CDGM(1,N)).

If \(\varphi \left({{M}_{j}}^{\left(1\right)}\left(k\right),{{M}_{j}}^{\left(1\right)}\left(k-1\right),\omega \right)=\frac{1}{2}\left(f({{m}_{j}}^{\left(1\right)}\left(k\right);\varpi )+f({{m}_{j}}^{\left(1\right)}\left(k-1\right);\varpi )\right)\)

Thus, Eq. (11) can be written as follows:

$${M}^{\left(0\right)}\left(k\right)={aZ}^{\left(1\right)}\left(k\right)+b{\left[{Z}^{\left(1\right)}\left(k\right)\right]}^{2}+\varphi \left({{M}_{j}}^{\left(1\right)}\left(k\right),{{M}_{j}}^{\left(1\right)}\left(k-1\right),\omega \right)$$
(12)

The whitening equation of the CDGM(1,N) model is as follows:

$$\frac{{dM}^{\left(1\right)}\left(t\right)}{dt}={aM}^{\left(1\right)}\left(t\right)+b{\left[{M}^{\left(1\right)}\left(t\right)\right]}^{2}+\varphi \left({{M}_{j}}^{\left(1\right)}\left(k\right),{{M}_{j}}^{\left(1\right)}\left(k-1\right),\omega \right)$$
(13)

Let \(\varphi \left({{M}_{j}}^{\left(1\right)}\left(k\right),{{M}_{j}}^{\left(1\right)}\left(k-1\right),\omega \right)=\lambda \left(k\right)\). Based on Eq. (13),

$$\frac{{dM}^{\left(1\right)}\left(t\right)}{dt}={aM}^{\left(1\right)}\left(t\right)+b{\left[{M}^{\left(1\right)}\left(t\right)\right]}^{2}+\lambda \left(k\right)$$
(14)

and

$$\begin{array}{c}\frac{{dM}^{\left(1\right)}\left(t\right)}{bdt}={\left[{M}^{\left(1\right)}\left(t\right)\right]}^{2}+\frac{a}{b}{M}^{\left(1\right)}\left(t\right)+\lambda \left(k\right)\\ \frac{{dM}^{\left(1\right)}\left(t\right)}{bdt}={\left[{M}^{\left(1\right)}{\left(t\right)}^{2}+\frac{a}{2b}\right]}^{2}+\frac{1}{b}\lambda \left(k\right)-\frac{{a}^{2}}{4{b}^{2}}\end{array}$$

Let \(n=-\frac{a}{2b},\omega \left(k\right)=\frac{1}{b}\lambda \left(k\right)-\frac{{a}^{2}}{4{b}^{2}}k=\mathrm{1,2},\cdots n\). Thus, we have the following:

$$\frac{{dM}^{\left(1\right)}\left(t\right)}{bdt}={\left[{M}^{\left(1\right)}{\left(t\right)}^{2}-n\right]}^{2}+\omega \left(k\right)$$
(15)

Integrating both parts of Eq. (15):

$$\int {dM}^{\left(1\right)}\left(t\right)=\int \left\{{\left[{M}^{\left(1\right)}{\left(t\right)}^{2}-n\right]}^{2}+\omega \left(k\right)\right\}bdt$$

and

$$\int \frac{{dM}^{\left(1\right)}\left(t\right)}{{\left[{M}^{\left(1\right)}{\left(t\right)}^{2}-n\right]}^{2}+\omega \left(k\right)}=\int bdt$$
(16)

Because \(\omega \left(k\right)\) is a constant, Eq. (16) is the Riccati equation. From the literature (Duan and Pang 2021), we can obtain the time response function of the CDGM(1,N) model:

  1. (1)

    When \(\omega \left(k\right)<0\),\({C}_{1}=\frac{1}{2\sqrt{\omega \left(1\right)}}ln\left|\frac{{m}^{\left(1\right)}\left(1\right)+n-\sqrt{\omega \left(1\right)}}{{m}^{\left(1\right)}\left(1\right)+n+\sqrt{\omega \left(1\right)}}\right|-b\)

    $${\widehat{M}}^{\left(1\right)}\left(k\right)=\frac{\sqrt{\omega \left(k\right)}-n\mp \left(\sqrt{\omega \left(k\right)}-n\right){e}^{2\sqrt{\omega \left(k\right)}\left(bk+{C}_{1}\right)}}{1\pm {e}^{2\sqrt{\omega \left(k\right)}\left(bk+{C}_{1}\right)}}k=\mathrm{1,2},\cdots n$$
    (17)
  2. (2)

    When \(\omega \left(k\right)=0\),\({C}_{2}=-\frac{1}{{m}^{\left(1\right)}\left(1\right)+n}-b\), and

    $${\widehat{M}}^{\left(1\right)}\left(k\right)=-\frac{1}{bk+{C}_{2}}-n,k=\mathrm{1,2},\cdots n$$
    (18)
  3. (3)

    When \(\omega \left(k\right)>0\), \({C}_{3}=\frac{1}{\sqrt{-\omega \left(1\right)}}arctan\frac{{m}^{\left(1\right)}\left(1\right)+n}{\sqrt{-\omega \left(1\right)}}-b\),

    $${\widehat{M}}^{\left(1\right)}\left(k\right)=\sqrt{-\omega \left(k\right)}tan\left[\sqrt{-\omega \left(k\right)}\left(bk+{C}_{3}\right)\right]-nk=\mathrm{1,2},\cdots n$$
    (19)
  4. (4)

    The reduction value is obtained as follows:

    $${\widehat{M}}^{\left(0\right)}\left(k\right)={\widehat{M}}^{\left(1\right)}\left(k\right)-{\widehat{M}}^{\left(1\right)}\left(k-1\right),k=\mathrm{2,3},\cdots ,n$$
    (20)

Neural network-carbon emission dynamic system grey model

In Eq. (4) of the evolutionary dynamic system of carbon emissions, the control function \(f\left({M}_{1}\left(t\right);\omega \right)\) has many influencing factors, including energy consumption and GDP, so it can be used as a control function and redefined through neurons (Ma et al. 2021). Thus, it can be set as follows:

$$\varphi \left({{M}_{j}}^{\left(1\right)}\left(k\right),{{M}_{j}}^{\left(1\right)}\left(k-1\right),\theta \right)=\sum_{j=1}^{l}{\beta }_{j}g\left({{m}_{j}}^{\left(1\right)}\left(k\right),{{m}_{j}}^{\left(1\right)}\left(k-1\right),{\omega }_{j},{c}_{j}\right)+c$$

where \(l\) indicates the number of sequences related to the control function, and \({{m}_{j}}^{\left(1\right)}\left(k\right)\) is obtained from Eqs. (8)–(9). Thus, based on the CDGM(1,N) model, the following model can be defined:

Definition 2

Let \({M}^{\left(0\right)},{M}^{\left(1\right)},{Z}^{\left(1\right)}\) as shown in the definition of Eqs. (4)–(6). Then,

$${M}^{\left(0\right)}\left(k\right)={aZ}^{\left(1\right)}\left(k\right)+b{\left[{Z}^{\left(1\right)}\left(k\right)\right]}^{2}+\sum_{j=1}^{l}{\beta }_{j}g\left({{m}_{j}}^{\left(1\right)}\left(k\right),{{m}_{j}}^{\left(1\right)}\left(k-1\right),{\omega }_{j},{c}_{j}\right)+c$$
(21)

This is called the novel grey prediction model with a feedforward neural network based on a carbon emission dynamic evolution system (NN-CDGM(1,N)).

where \(g\left(\cdot \right)\) is the activation function, which is the single hidden layer neural network. Consider the following hidden layer function:

$$g\left(m,w,c\right)=\frac{2}{1+exp\left(-{w}^{T}m+c\right)}-\alpha$$

\(\alpha\) is the regulatory system, and the optimization is sought through a genetic algorithm. The specific methods can be found in the literature (Holland 1992).

Let \(W=\left({\omega }_{1},{\omega }_{2},\cdots ,{\omega }_{l}\right)\),\(C=\left(c,{c}_{1},{c}_{2},\cdots ,{c}_{l}\right)\). Based on Theorem 2,

$$\lambda \left(k\right)=\phi \left({{M}_{j}}^{\left(1\right)}\left(k\right),{{M}_{j}}^{\left(1\right)}\left(k-1\right),\omega \right)=\sum_{j=1}^{l}{\beta }_{j}g\left({{m}_{j}}^{\left(1\right)}\left(k\right),{{m}_{j}}^{\left(1\right)}\left(k-1\right),{\omega }_{j},{c}_{j}\right)+c$$

Thus, the time response of the NN-CDGM(1,n) model is calculated by using Eqs. (16)–(19).

Next, the Levenberg–Marquardt (LM) algorithm (Holland 1992) is used to compute the neural grey system model. Let \(\theta ={\left(\beta ,W,C\right)}^{T}\), \(\beta =\left({\beta }_{1},{\beta }_{2},\cdots ,{\beta }_{l}\right)\), \(W=\left({\omega }_{1},{\omega }_{2},\cdots ,{\omega }_{l}\right)\),\(C=\left(c,{c}_{1},{c}_{2},\cdots ,{c}_{l}\right)\). For convenience, the training error of each point is defined as follows:

$${e}_{k}={M}^{\left(0\right)}\left(k\right)-{aZ}^{\left(1\right)}\left(k\right)-b{\left[{Z}^{\left(1\right)}\left(k\right)\right]}^{2}-\sum_{j=1}^{l}{\beta }_{j}g\left({{m}_{j}}^{\left(1\right)}\left(k\right),{{m}_{j}}^{\left(1\right)}\left(k-1\right),{\omega }_{j},{c}_{j}\right)+c$$

Let \(\theta ={\left(\beta ,W,C\right)}^{T}\),\(\beta =\left({\beta }_{1},{\beta }_{2},\cdots ,{\beta }_{l}\right)\),\(W=\left({\omega }_{1},{\omega }_{2},\cdots ,{\omega }_{l}\right)\),\(C=\left(c,{c}_{1},{c}_{2},\cdots ,{c}_{l}\right)\). The sum of squared errors can be expressed as follows:

$$\begin{array}{c}{E}_{D}\left(a,b,\theta \right)=\sum\limits_{k=2}^{n}{e}_{k}^{2}={e}^{T}e\\ -{\left({\Delta }^{2}{E}_{D}\left(a,b,\theta \right)\right)}^{-1}{E}_{D}\left(a,b,\theta \right)\end{array}$$

where the first-order gradient can be defined as follows:

$${E}_{D}\left(a,b,\theta \right)={J}^{T}e$$

The second gradient can be given by a Taylor series:

$${E}_{D}\left(a,b,\theta \right)={J}^{T}J+S$$

Here, the S matrix is usually assumed to be the O matrix because its elements are the second partial derivatives of the error. The Jacobian formula is as follows:

$$J=\left[J\left(a\right),J\left(b\right),J\left(\beta \right),J\left(W\right),J\left(C\right)\right]$$
(22)

where

$$\begin{array}{ccc}J\left(a\right)={\begin{pmatrix}\frac{\partial e_2}{\partial a}\\\frac{\partial e_3}{\partial a}\\\vdots\\\frac{\partial e_n}{\partial a}\end{pmatrix}}_{\left(n-1\right)\times1},&J\left(a\right)={\begin{pmatrix}\frac{\partial e_2}{\partial b}\\\frac{\partial e_3}{\partial b}\\\vdots\\\frac{\partial e_n}{\partial b}\end{pmatrix}}_{\left(n-1\right)\times1},&J(\beta)={\begin{pmatrix}\frac{\partial e_2}{\partial\beta_1}&\frac{\partial e_2}{\partial\beta_2}&\cdots&\frac{\partial e_2}{\partial\beta_l}\\\frac{\partial e_3}{\partial\beta_1}&\frac{\partial e_3}{\partial\beta_2}&\cdots&\frac{\partial e_3}{\partial\beta_2}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial e_n}{\partial\beta_1}&\frac{\partial e_n}{\partial\beta_1}&\cdots&\frac{\partial e_n}{\partial\beta_1}\end{pmatrix}}_{(n-1)\times l}\\J(W)={\begin{pmatrix}\frac{\partial e_2}{\partial\omega_1}&\frac{\partial e_2}{\partial\omega_2}&\cdots&\frac{\partial e_2}{\partial\omega_{2l}}\\\frac{\partial e_3}{\partial\omega_1}&\frac{\partial e_3}{\partial\omega_2}&\cdots&\frac{\partial e_3}{\partial\omega_{2l}}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial e_n}{\partial\beta_1}&\frac{\partial e_n}{\partial\beta_1}&\cdots&\frac{\partial e_n}{\partial\beta_1}\end{pmatrix}}_{(n-1)\times2l}&&J(C)={\begin{pmatrix}\frac{\partial e_2}{\partial c}&\frac{\partial e_2}{\partial c_1}&\cdots&\frac{\partial e_2}{\partial c_l}\\\frac{\partial e_3}{\partial c}&\frac{\partial e_3}{\partial c_1}&\cdots&\frac{\partial e_3}{\partial c_l}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial e_n}{\partial c}&\frac{\partial e_n}{\partial c_1}&\cdots&\frac{\partial e_n}{\partial c_l}\end{pmatrix}}_{(n-1)\times(l+1)}\end{array}$$
(23)

The LM algorithm uses the error vector and Jacobian matrix to calculate the inverse matrix of \({J}^{T}J\), experimentally scales the identity matrix to avoid an inappropriate matrix, and finally updates the parameters as follows:

$${\left(\begin{array}{c}a\\ b\\ \theta \end{array}\right)}^{l+1}={\left(\begin{array}{c}a\\ b\\ \theta \end{array}\right)}^{l}-{({J}^{T}J+\mu I)}^{-1}{J}^{T}e$$
(24)

where the coefficient \(\mu\) of the scaled identity matrix is updated with the change in \({E}_{D}(a,b,\theta )\), and the calculation scheme is updated in Martin and Mohammad (1994).

The modeling steps of NN-CDGM(1,N)

To evaluate the validity and accuracy of the model, the APE, MAPE, MAE, RMSE, and R2 metrics are defined as follows. The evaluation criteria of MAPE are shown in Eq. (27) (Javed et al. 2020). The smaller the MAE and RMSE values are, the better the model performance is. The larger the value of R2 is, which is closer to 1, the better the model performance is.

$$\mathrm{APE}=\left|\frac{{x}^{\left(0\right)}\left(i\right)-{\widehat{x}}^{\left(0\right)}\left(i\right)}{{x}^{\left(0\right)}\left(i\right)}\right|\times 100\%,i=\mathrm{1,2},\cdots ,n$$
(25)
$${\text{MAPE}}=\frac{1}{n-1}\left(\sum_{i=1}^{n}\mathrm{APE}\right)$$
(26)
$${\text{MAPE}}(\%)=\left\{\begin{array}{ll}\;\;<10&\;\; \text{Highly accuracy forecast}\\ \begin{array}{c}10-20\\ \begin{array}{l}20-50\\ >50\end{array}\end{array}& \begin{array}{l}\text{Good forecast}\\ \begin{array}{l}\text{Reasonanle forecast}\\ \text{Inaccurate forecas}\end{array}\end{array}\end{array}\right.$$
(27)
$$\mathrm{MAE}=\frac{\sum\limits_{i=1}^{N}\left|{y}_{i}-{\widehat{y}}_{i}\right|}{N}$$
(28)
$${\text{RMSE}}=\sqrt{\frac{1}{N}\sum_{\mathrm{i}=1}^{N}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}$$
(29)
$${R}^{2}=1-\frac{\sum\limits_{i=1}^{N}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}{\sum\limits_{i=1}^{N}{\left({y}_{i}-{\overline{y} }_{i}\right)}^{2}}$$
(30)

Based on the NN-CDGM(1,N) model established in sections “Neural network-carbon emission dynamic system grey model” and “The modeling steps of NN-CDGM(1,N),” the main prediction process of the model is introduced below.

  • Step 1. Input raw data \({M}^{\left(0\right)}\left(k\right)\) as the main sequence; \({{M}_{j}}^{\left(0\right)}\left(k\right)\left(j=1,2,3,4\right)\) are coal consumption, crude oil consumption, GDP, and population, respectively, and are the relevant sequences.

  • Step 2. The 1-AGO sequence \({M}^{\left(1\right)}\left(k\right)\) of \({M}^{\left(0\right)}\left(k\right)\), \({{M}_{j}}^{\left(0\right)}\left(k\right)\left(j=1,2,3,4\right)\) and the mean value sequence \({z}^{\left(1\right)}\) of \({{M}_{j}}^{\left(1\right)}\left(k\right)\left(j=1,2,3,4\right)\) are calculated.

  • Step 3. By substituting the data obtained in Step 2 into Eqs. (22)–(24), parameters \(a,b,{\beta }_{j},{c}_{j},c\) can be obtained.

  • Step 4. The parameters obtained in Step 3 are substituted into Eqs. (17)–(20). The different time response functions are used to obtain simulated and reduced values.

  • Step 5. In step 4, the APE and MAPE values can be obtained, and then, the genetic algorithm is used to optimize the activation function to obtain the optimal \(\alpha\) value, where \({M}^{\left(0\right)}\) is obtained when the lowest MAPE value is calculated.

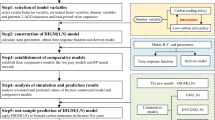
The brief calculation process is shown in Fig. 3.

Fig. 3
figure 3

Flowchart of the NN-CDGM(1,N) model

Full size image

Validity analysis

In this section, the validity of the model is first verified. The 10-year data on Beijing’s carbon emissions are divided into two types of modeling objects. For the first type, the first 8 data points are used for simulation, and the last 2 data points are used for prediction. For the second type, the first 7 data points are used for simulation, and the last 3 data points are used for prediction. At the same time, the validity of 9 data points is analyzed. The modeling objects are also divided into two types: For the first type, the first 7 data points are used for simulation, and the last 2 data points are used for prediction. For the second type, the first 6 data points are used for simulation, and the last 3 data points are used for prediction. Compared with the other five classic grey multivariable models, all of them have good effects. Finally, the best model is selected to predict the carbon emissions of Beijing in the 2019–2023 period.

Because the carbon emission system is a complex dynamic system, many factors affect carbon emissions. In this section, four factors, including coal consumption, crude oil consumption, GDP, and population, are selected as influencing factors, and the NN-CDGM(1, N) model is used to analyze the data on Beijing’s carbon emissions. The specific data on Beijing’s carbon emissions, coal consumption (hundred thousand tons), crude oil consumption (hundred thousand tons), GDP (billions of dollars), and population (hundred thousand people) are given in Table 1.

Table 1 Carbon emissions, coal consumption, crude oil consumption, GDP, and population of Beijing from 2009 to 2018
Full size table

Efficiency analysis of the NN-CDGM(1,N) model

Regarding the data in Table 1, carbon emissions are taken as the main sequence; coal consumption, crude oil consumption, GDP, and population are taken as the relevant sequences; and the modeling steps of the NN-CDGM(1,N) model in “The modeling steps of NN-CDGM(1,N)” are used to model and forecast carbon emissions. Data of different lengths are selected for modeling, and the calculated results are compared with the classic first-order multivariable grey prediction models: GM(1,N) (Liu and Lin 2011), GMVM(1,N) (Jiang et al. 2020), GMC(1,N) (Tien 2005), and GOM(1,N) (Wu et al. 2015).

Regarding the data from 2009 to 2018, 8 data points are used for modeling, and 2 data points are used for prediction (case 1); additionally, 7 data points are used for modeling, and 3 data points are used for prediction (case 2). Regarding the data from 2010 to 2018, 7 data points are used for modeling, and 2 data points are used for prediction (case 3); additionally, 6 data points are used for modeling, and 3 data points are used for prediction (case 4).

Case 1. 8 data points for modeling and 2 data points for prediction

Eight data points from 2009 to 2016 are used for modeling, and the 2-year carbon emissions of Beijing from 2017 to 2018 are predicted. Finally, the modeling and prediction results are compared with those of the GM(1,N), GMVM(1,N), GOM(1,N), and GMC(1,N) models and analyzed. The specific results are shown in Table 3. The calculation results of the model parameters are as follows:

$${M}^{\left(0\right)}\left(k\right)=-0.0391{Z}^{\left(1\right)}\left(k\right)+\begin{array}{c}2.265E-05\end{array}{\left[{Z}^{\left(1\right)}\left(k\right)\right]}^{2}+\sum_{j=1}^{l}{\beta }_{j}g\left({{m}_{j}}^{\left(1\right)}\left(k\right),{{m}_{j}}^{\left(1\right)}\left(k-1\right),{\omega }_{j},{c}_{j}\right)\begin{array}{c}-0.9883\end{array}$$

where

$$\begin{array}{c}\beta =\left(-5.1840,-5.3631,-5.4956,-5.0651\right)\\ \omega =\left(\left(0.2613,0.5678\right),(0.9615,0.6130),(0.4976,0.8070),(0.4278,0.8808\right)\\ c=\left(0.0892,0.3131,0.6074,0.3787\right)\end{array}$$

Table 2 shows that all indexes of NN-CDGM(1,N) are the best, and the R2 value is very close to 1, indicating that the simulated value closely matches the real value. In the simulation stage, the MAPE values of the NN-CDGM(1,N), GM(1,N), and GOM(1,N) models are all less than 5%, and the fitting effect is good. However, in the prediction stage, only the NN-CDGM(1,N) model has an accuracy below 5%. To further compare the differences between models, Fig. 4 is drawn based on the information in Table 2. The results of GMC(1,N) have negative values, which is inconsistent with reality. Thus, this model is not shown in Fig. 4.

Table 2 Comparison of the results of multiple models based on 8 data points for modeling and 2 data points for prediction
Full size table
Fig. 4
figure 4

Comparison of the results of each model based on 8 data points for modeling and 2 data points for prediction

Full size image

Figure 4(a) clearly illustrates that the GMVM(1,N) model is always above the actual data and finally shows a sudden increasing trend with a large error. To compare the other models more clearly, GMVM(1,N) is removed, and Fig. 4(b) is shown. Clearly, the curve of the NN-CDGM(1,N) model is most consistent with the actual data curve. Although the MAPE values of the GM(1,N) and GOM(1,N) models are also very small, both models are clearly below the actual data at the front end of the data, and both show a sudden decreasing trend in the prediction stage, which is inconsistent with the actual curve trend. Therefore, the performance of the NN-CDGM(1,N) model is better in this case.

Case 2. 7 data points for modeling and 3 data points for prediction

In this case, 7 data points from 2009 to 2015 are used to model and predict the carbon emissions of Beijing over the 3 years from 2016 to 2018. Finally, the modeling and prediction results are compared with those of the above comparison models and analyzed, and the specific results are shown in Table 3.

Table 3 Comparison of the results of multiple models based on 7 data points for modeling and 3 data points for prediction
Full size table

Table 3 shows that the MAPE value of GMC(1,N) is 1.4467%, which is the smallest among all the models, but its MAPE value is 39.1946%, showing a poor prediction effect. Its R2 is negative, and the simulated value does not match the real value. In general, the simulation effect of NN-CDGM(1,N), GM(1,N), and GOM(1,N) is better than that of the other models, but the overall error of NN-CDGM(1,N) is the smallest. To further compare the model fitting and prediction effects, Table 3 is converted into Fig. 5. GMVM(1,N) yields negative values, which are not shown in the figure.

Fig. 5
figure 5

Comparison of the results of each model based on 7 data points for modeling and 3 data points for prediction

Full size image

As illustrated in Fig. 5, the actual data show a relatively gentle fluctuation trend and eventually show a slight increase. The GMC(1,N) and NN-CDGM(1,N) models are most consistent with the actual data, especially in the simulation stage, when the GMC(1,N) model almost coincides with the actual data, but there is a sudden increase in the prediction stage, and the overall effect is not good. However, the NN-CDGM(1,N) model always fluctuates near the actual curve, and the final trend is consistent with the actual data. Thus, it is relatively superior overall.

Case 3. 7 data points for modeling and 2 data points for prediction

In this case, 7 data points from 2010 to 2016 are used to model and forecast the carbon emissions of Beijing for the 2 years from 2017 to 2018. Finally, the modeling and prediction results are compared with those of the above comparison models and analyzed, and the specific results are shown in Table 4.

Table 4 Comparison of the results of multiple models based on 7 data points for modeling and 2 data points for prediction
Full size table

Table 4 shows that for this set of data, the prediction errors of all models are above 5%, and the NN-CDGM(1,N) model has the best prediction effect. On the whole, the indexes of the NN-CDGM(1,N) model are also optimal, and the RMSE is significantly better than that of the comparison models. To observe the data trend more intuitively, Table 4 is plotted in Fig. 6. Similar to the figures above, GMC(1,N) yields negative values, which are not shown in this figure.

Fig. 6
figure 6

Comparison of the results of each model based on 7 data points for modeling and 2 data points for prediction

Full size image

Figure 6(a) clearly shows that the GMVM(1,N) model has a large error with the actual data; therefore, it is removed from Fig. 3(b) for further comparison. In Fig. 6(b), NN-CDGM(1,N), GM(1,N), and GOM(1,N) all fluctuate near the actual data. However, the last two models show irregular fluctuations and are different from the trend of the actual data; thus, the prediction effect is not good. The curve of NN-CDGM(1,N) is always near the actual data curve. It is closest to the actual data, and therefore, the simulation and prediction effects in relation to the comparison models are the best.

Case 4. 6 data points for modeling and 3 data points for prediction

In this case, 6 data points from 2010 to 2015 are used for modeling, and the 3-year carbon emissions of Beijing from 2016 to 2018 are predicted. Finally, the modeling and prediction results are compared with those of the above comparison models and analyzed, and the specific results are shown in Table 5.

Table 5 Comparison of the results of multiple models based on 6 data points for modeling and 3 data points for prediction
Full size table

Table 5 shows that each evaluation index of the NN-CDGM(1,N) model is significantly better than that of the comparison model. The prediction results of the GMVM(1,N) models contain negative values, which is inconsistent with the actual situation. The NN-CDGM(1,N), GM(1,N) and GOM(1,N) models all have small simulation errors, but only the NN-CDGM(1,N) model has a prediction error of less than 10%, and its simulation error is also the smallest among all models. Figure 7 clearly compares the trends and fitting degrees of the models. The GMVM(1,N) model yields negative values, which are not shown in the figure.

Fig. 7
figure 7

Comparison diagram of the results of each model based on 6 data points for modeling and 3 data points for prediction

Full size image

Figure 7 illustrates that, except for the NN-CDGM(1,N) model, the other three models all show significant volatility. Among them, the GMC(1,N) model has a trend that is similar to the actual data, but the range is large. The other two models show irregular and large fluctuations, which is inconsistent with the actual data trend; thus, the overall effect is poor. The NN-CDGM(1,N) model is consistent with the actual data trend, the curve is relatively close, and the effect is better.

Case summary

Based on the above four cases, the results obtained by the same model from different modeling objects vary. Due to the volatility of the original data, the NGM(1,N), GMVM(1,N), and GMC(1,N) models all show negative values in this case, which is not in line with the actual situation, while the GM(1,N) and GOM(1,N) models show mutations in the simulation and prediction stages, respectively, making the overall effect poor.

However, the simulation and prediction accuracy of the four cases of the NN-CDGM(1,N) model are all approximately 5%, the models all perform well, and the results are close to the actual data, indicating that the performance of this model is relatively stable when modeling data of different lengths, and it is relatively less affected by the data length. The NN-CDGM(1,N) model is thus effective for predicting carbon emissions and has a good stability and adaptability.

All the calculation results of the NN-CDGM(1,N) model in the four cases are shown in Table 6 below.

Table 6 Modeling and forecasting results of the NN-CDGM(1,N) model of carbon emissions in Beijing from 2009 to 2018
Full size table

Table 6 shows that although the average error of the simulation and prediction of the four groups of results is less than 10% and all of them show a good performance, due to the different lengths of modeling data, the performance of the NN-CDGM(1,N) model also varies in each case. A further comparison shows that the evaluation indexes of case 1 are basically optimal, and the MAE and RMSE values are both small, indicating that the overall error is small, and the R2 value is 0.84, close to the maximum value of 1, which means that the simulated value of the model matches the real value, and the model performance is good.

In conclusion, compared with multiple comparison models, the NN-CDGM(1,N) model proposed in this paper performs better in the four cases of predicting carbon emissions in Beijing, and the performance of modeling different lengths of data is relatively stable. In addition, by comparing the NN-CDGM(1,N) model among the four cases, the overall performance of case 1 is the best. Therefore, the NN-CDGM(1,N) model calculated from case 1 is selected to predict the emissions in the next 5 years.

Application

Forecast of carbon emissions in Beijing from 2019 to 2023

The above validity analysis shows that for the same set of data, there will be some differences in the results when different lengths of data are used for modeling (see Fig. 8 for details). Among the five comparison models, the simulation performance of the GOM(1,N) and GMVM(1,N) models is better than the prediction performance. GM(1,N) and GMC(1,N) fluctuate greatly at the beginning of the simulation, and the predicted values in different cases are relatively scattered.

Fig. 8
figure 8

Comparison of the modeling and prediction results of different lengths of data in the same model

Full size image

The actual data fluctuate between 90 and 105, but the simulated values of the comparison model range from 50 ~ 110 (GM(1,N) model) to − 700 approx. 400 (GMVM(1,N) model). Although three cases of the NN-CDGM(1, N) model in Fig. 9 show some deviation from the actual results, the fluctuation is still controlled between 75 and 105, which is relatively stable. Table 6 and Fig. 9 show that when the NN-CDGM(1, N) model uses the same data, the model performance is not completely the same, but the difference is within 20, which is relatively stable.

Fig. 9
figure 9

Comparison of the results of the NN-CDGM(1,N) model with different lengths

Full size image

In summary, the NN-CDGM(1,N) model yields different results for different modeling objects but is relatively stable and can effectively simulate and predict carbon emissions. In addition, the performance of the NN-CDGM(1,N) model in the four cases is observed and compared through Fig. 9. Clearly, the simulation and prediction results are the best when the data from 2009 to 2018 are selected, 8 data points are used for modeling, and 2 data points are used for prediction. Therefore, the modeling results of these data are selected to predict the carbon emissions of Beijing from 2019 to 2023, and the specific results are shown in Table 7.

Table 7 Prediction results of carbon emissions in Beijing from 2019 to 2023
Full size table

The actual data from 2009 to 2018 in Fig. 9 show that the overall carbon emissions in Beijing have experienced a slight downwards trend with fluctuations, and the data in 2018 were in the early stage of rising fluctuations. The prediction results of the NN-CDGM(1,N) model for the next 5 years indicate that Beijing’s carbon emissions will experience a slight upwards trend, which is consistent with the fluctuation trend of the actual data.

Discussion and policy recommendations

Based on the relevant data used in the modeling (Table 1), over the past decade, Beijing’s population growth has been small, coal and oil consumption has continued to decline, but the city’s GDP has continued to increase, indicating that Beijing’s policies and measures to optimize the industrial structure and support the clean energy transition have been very effective.

From the prediction results in Table 7, in the next 5 years, Beijing’s carbon emissions will show a fluctuation trend, first declining and then rising, which is consistent with the previous fluctuation trend and conforms to the actual situation. In addition, carbon emissions are basically controlled below 90, although still a slight upwards trend is still apparent, and the growth rate is decreasing year by year and only increasing by less than 2% compared with 2018. This suggests that Beijing has entered the reduction platform period and needs to continue to implement effective measures to meet the existing conditions for further breakthroughs. We must continue to strictly control carbon emissions, further improve programs and measures, gradually introduce emission standards for industries, and better control the carbon emissions of industries and products with high levels of energy consumption and emissions to achieve the goal of continuously reducing carbon emissions.

Conclusions

Carbon emissions affect the future development of the world. The scientific and effective prediction and analysis of carbon emission data are very important for the country and the government to implement corresponding measures. The global energy mix has undergone major changes in recent years, and the COVID-19 pandemic has exacerbated the problem. Historical data on energy consumption and carbon emissions no longer apply to current realities.

First, the existing carbon emission prediction methods are mostly based on data and seldom consider the characteristics of the carbon emission system. Therefore, based on the background of the carbon emission dynamic system, this paper introduces a dynamic model with an external function. Second, considering the advantages of the grey prediction model in the application of small sample data, a dynamic grey prediction model of carbon emissions is established. Finally, the carbon emission system is affected by many factors, and the feedforward neural network model is introduced to calculate the function of other external factors in the calculation process.

This model is based on the dynamic system of the carbon emission system. Grey theory is used as the foundation, and the computational advantages of the neural network model are leveraged to yield results that are consistent with the actual change in carbon emissions. In the application process, the effectiveness of the model is verified by considering different modeling objects, and the results show that the NN-CDGM(1,N) model is basically better than other grey prediction models in the application of carbon emissions and that the model can effectively predict the carbon emissions of Beijing in the next 5 years.

This paper makes three major contributions: (1) the grey prediction model is established based on the carbon emission system; therefore, the scope of the grey prediction model is expanded from the aspect of the modeling structure. (2) In the process of modeling and calculation, the grey prediction model is organically combined with a neural network, which makes the model suitable for small sample data. (3) The NN-CDGM(1,N) model can effectively predict the carbon emissions of Beijing, China.

The model shows a good performance in this application, but some problems remain. In future research, the existing model can be further optimized based on the model structure and modeling mechanism, the selection of relevant factors, data pre-processing, and parameter optimization. The effectiveness of the model for predicting carbon emissions can be further verified through theoretical derivation and the use of additional data. The model features can be generalized, while retaining the good modeling properties, and applied to other domains. These questions need to be further discussed and studied in the future.