Introduction

All the developing nations, including India, face the problem related to vehicular noise due to a continuous exponential increase in the number of vehicles on the road, which ultimately increases the environmental noise levels (Singh et al. 2016a). It has been estimated that more than 50% of the environmental noise is contributed from road traffic (D. Banerjee et al. 2008; El-Fadel et al. 2002; Tandel et al. 2011). Traffic noise causes deterioration of people’s comfort and quality of life, residing close to the transportation infrastructure (Dibyendu Banerjee 2012). Although transportation infrastructure is the essential requisite for any developing society, its negative aspects have received no or little attention as it provides means for satisfying the mobility and accessibility demand (Hamad et al. 2017). This has led to a range of environmental problems, including traffic noise. Authorities worldwide have focused more on the issues related to air, water, and soil pollution, but noise pollution hasn’t received its due share (K. Kumar et al. 2011), which may be due to the property of being invisible besides having profound implications only in the long run (Dratva et al. 2010; Foraster et al. 2014; Lercher 1996; Seidler et al. 2016). However, recent research has projected noise as a severe pollutant that can cause both physiological and psychological effects. The effects include annoyance (Ouis 2001), hypertension(Barregard et al. 2009; Chang et al. 2011), sleep disturbance (Halperin 2014; Jakovljević et al. 2006), hearing mechanism dysfunction (Barrigón Morillas et al. 2002), myocardial infarction (Babisch et al. 2005; Paunovic and Belojević 2014; Selander et al. 2009), cardiovascular diseases(Begou et al. 2020; Davies and Van Kamp 2012; T. Munzel et al. 2014; Thomas Munzel et al. 2018), metabolic diseases like diabetes (Dzhambov 2015; Mette et al. 2013), and psychotropic medication use (Okokon et al. 2018). Based on the studies reported and growing evidence, the focus has shifted toward transportation-related noise pollution for its proper control and management.

The paper is structured in the following manner. The “Some of the developed traffic noise models” section gives an overview about the various traffic noise models that have been developed in various countries along with the parameters used for modeling purposes. Following this, the “Graph-theoretic approach” section provides an introduction about the GTA (graph-theoretic approach) for modeling purposes besides giving a brief list about the various advantages of using this technique. The “Methodology” section provides the methodology adopted for developing the models. The “Results” section presents the results and validation of the model. This is followed by the “Discussion” section while the “Strengths and limitations” section presents the strengths, limitations, and future scope of the work. This is followed by the “Conclusions” section.

Some of the developed traffic noise models

Traffic noise models play an essential role in designing acoustic friendly roads and assessing traffic noise’s impact on the residents living near the transportation infrastructure like highways and major roads. (Pamanikabud and Tansatcha 2003; Rajakumara and Mahalinge Gowda 2009). Several mathematical models have been developed worldwide to estimate RTN (road traffic noise) levels, using the data for the parameters used for modeling purposes. However, given the noise’s stochastic nature, it can be described quantitatively using the estimate of certain indices, and its actual value is known only to mother nature (Farrelly and Brambilla 2003). The development of traffic noise models is not a new procedure, and continuous improvements have occurred over time. These include considering the vehicular noise in a different perspective (i.e., rolling noise and engine noise), the effect of road pavements, the effect of temperature, the effect of screening from the nearby walls, ground effects, and atmospheric absorption. Improvements have also occurred in terms of the methods used for developing models. In addition to generally used regression analysis (Agarwal and Swami 2011; Rajakumara and Mahalinge Gowda 2009), techniques such as artificial neural networks (ANN) (Cammarata et al. 1995; Givargis and Karimi 2010), genetic algorithms (GA) (Gündoğdu et al. 2005; Rahmani et al. 2011), decision trees (DT) (Quinlan 1986), and random forests (RF) (Singh et al. 2016a) have been successfully used.

Different traffic noise models like FHWA (Federal Highway Administration), CoRTN (Calculation of Road Traffic Noise), and RLS-90 predict the noise levels based on the corrections applied to a mean reference energy level (A-weighted peak pass-by noise level generated by a single moving vehicle at a distance of 15m using a sound level meter placed at the height of 1.5m above the ground) (Steele 2001). These models have been applied to the traffic scenarios of the developed countries (for which they were originally developed) successfully for a long period with data about the relevant parameters. Modifications in some of these models for specific regions have also been made (Givargis and Mahmoodi 2008). Some of the parameters usually considered include traffic volume (Gulliver et al. 2015); the distance of measuring point from traffic lane; vehicular speed (Johnson and Saunders 1968; P. Kumar et al. 2014); percentage of heavy vehicles (To WM et al. 2002); road pavement surface (Cho and Mun 2008); gradient (Tang and Tong 2004); reflection from surrounding surfaces (Thorsson and Ögren 2005); the equivalent number of vehicles (Rahmani et al. 2011); driver characteristics like gender, skill, reaction time (Calvo et al. 2012), road bumps (Radhiah Bachok et al. 2017), and acceleration/deceleration; traffic congestion, and traffic signals (Can et al. 2008; StoIlova and StoIlov 1998).

These parameters have been used worldwide by researchers for traffic noise modeling. Modeling the dynamic aspects of traffic noise arising due to vehicle interaction and congestion near roundabouts was done by Chevallier et al. (Chevallier et al. 2009). The model uses a traffic flow simulation tool along with a sound propagation model and noise emission laws. Monte Carlo technique based noise prediction model was developed to include the uncertainty during the estimation of traffic noise (Lam and Tam 1998). A statistical model for urban settings was developed by Calixto et al. (Calixto et al. 2003). Based on neural networks, a model was developed for Indian traffic conditions by Kumar et al. (P. Kumar et al. 2014). The model achieved a good fit but lacked the usage of a large sample size. Another model based on neural networks was developed for New Delhi, India (N. Garg et al. 2015). The study utilized the classified traffic volume and classified vehicular speeds as the relevant parameters. A comparison between linear regression and neural network methods of prediction revealed that neural networks outperformed the linear regression technique. A study conducted in Patiala, Punjab, was done using four soft computing techniques of neural networks, decision trees, random forests, and generalized linear models (Singh et al. 2016a). The parameters used included traffic volume, traffic speed, and the percentage of heavy vehicles. The study revealed that the random forest approach was best suited for the study area’s traffic conditions. A study carried out in Nagpur, India used multiple linear regression for modeling the road traffic noise. The parameters included were traffic volume, speed and honking of light and heavy vehicles. The model provided an improvement in the noise prediction due to inclusion of honking as a parameter (Thakre et al. 2020). An open-source noise model using GIS (Geographic information system) for 2 British cities of Leicester and Norwich was developed by Gulliver et al. (Gulliver et al. 2015). Another model based on GIS was developed for road conditions in China (Li et al. 2002). The European Commission has undertaken the CNOSSOS-EU (Common noise assessment methods in Europe) project, making it mandatory for all the European member states to adopt a standard noise evaluation method out of a series of suggested models (Kephalopoulos et al. 2014). The models are to be evaluated based on simplicity, accuracy, precision, computational speed, and flexibility. A review on the principal traffic noise models like FHWA, CoRTN, RLS-90, ASJ RTN-2008, NMPB-routes 2008, and the CNOSSOS-EU model has been presented by Garg and Maji (Naveen Garg and Maji 2014). Comparisons have been made based on source modeling and sound propagation algorithm.

Genetic algorithms have also been used for modeling traffic noise. A study conducted in Erzurum city in eastern Turkey modeled traffic noise based on classified traffic volume, the maximum allowable noise level for a vehicle, road gradient, and building height ratio to road width (Gündoğdu et al. 2005). Another study conducted in Mashhad, Iran, used genetic algorithms for predicting noise levels using vehicle composition, speed, and traffic volume as the relevant parameters. The models were validated with in-field measurements (Rahmani et al. 2011). The traffic noise prediction model for Thailand was developed by Suksaard et al. (Suksaard et al. 1999). The model was based on classifying the vehicles as light and heavy vehicles and used vehicular speed as the relevant parameter. The model was found to be applicable up to 10 lane highways, up to a distance of 12m vertically, and up to a speed limit of 30 to 140 kmph.

The literature review reveals that different models have been developed for the prediction of RTN levels. The problem that arises in applying the standard models developed for western countries in developing countries is the variation in the local conditions that can affect the RTN. The nature of pavement surfaces, aged vehicles, heterogeneous traffic conditions, speed constraints, pavement width, and percentage of heavy vehicles differ from those used to develop some of the most commonly used models (Sisman and Unver 2011). Studies conducted by Prabat and Nagarnaik (Parbat and Nagarnaik 2008) concluded that India's traffic scenario is characterized by conditions like high levels of congestion, high noise levels, and low traffic facilities, and these differ significantly from the conditions prevalent in the European countries.

The present work is based on evaluating the suitability of GTA in predicting traffic noise levels for heterogeneous traffic conditions prevalent in developing countries like India. Most previous works have applied regression, neural networks, genetic algorithms, and GIS for the noise level prediction. However, GTA's application under Indian traffic conditions was found in very limited number of studies during the literature review. As per the authors, the study is probably one of the few studies in which the application of GTA for RTN level prediction is evaluated under heterogeneous traffic conditions. A brief introduction and usefulness of GTA are provided in the next section.

Graph-theoretic approach

The approach consists of identifying the traffic noise as a system that is composed of several subsystems. These subsystems are further comprised of parameters, and it is the interaction between these parameters that results in the outcome. There are several advantages of using GTA over other methods. Some of these advantages include

  • Many of the traditional models were developed to give the overall impact of the parameters considered. However, the traffic noise system is comprised of various subsystems that influence one another, and their interaction should not be ignored. This fact is readily incorporated in GTA.

  • It is simple, easy to use, and flexible in its application to various scenarios, where the direct application of traditional models may not be apt.

  • It has the flexibility of including subjective inputs, human opinions, and fuzziness of the real-life scenarios.

  • Being a matrix method, GTA can be utilized for computer programming when the number of variables and database is extensive.

All the subsystem variables considered and their interactions with each other are represented in the form of a matrix known as PFM (permanent function matrix). The model, along with the relevant parameters, is described in the form of a block diagram and then based on intuition, previous works, and expert opinion weights for the interaction terms are assigned (Prabhakaran et al. 2006; Ratha and Agrawal 2015). The inconsistencies that may arise due to improper human judgment are taken care of using the Eigenvalue approach, as has been proved in the pioneering work of Hwang and Yoon (Hwang and Yoon 1981). The PFM is then updated, and permanent of the updated matrix is calculated as shown in Eq. 1:

$$ Perm(A)=\sum \limits_{\sigma \in {S}_n}\prod \limits_{i=1}^n\left({a}_{i,\sigma (i)}\right), where $$
(1)

∏ represents the product function; σ(i) represents the ith member of the ‘n’ permutation groups;∑ represents the sum of the terms where each term is the product of ai, σ(i) for i = ‘1’ to ‘n’ for a ‘n x n’ matrix. The sum extends over all elements σ of the symmetric groupSn; i.e., over all the permutations of the numbers 1, 2…n.

Methodology

A systems approach has been utilized for modeling traffic noise. Usually, the RTN system consists of various subsystems that contribute to the area's overall acoustic scenario. The subsystems are themselves comprising of parameters that would influence the total noise produced. The traffic noise system, along with its relevant subsystems, is shown in Fig. 1 below:

Fig. 1
figure 1

Components of the road traffic noise system along with the respective parameters

Full size image

In the present study, five road traffic subsystem parameters were considered for modeling the traffic noise. The parameters were selected based on the literature review, which revealed that traffic noise levels are mostly modeled using parameters like traffic volume, traffic speed, number of heavy vehicles, road width, and gradient. The selected parameters included traffic volume per hour (S1) (excluding the volume of heavy vehicles like buses and trucks); carriageway width, in meters (S2); average traffic speed, in kmph (S3); number of heavy vehicles (S4) per hour; and number of honking events (S5) per hour. The selected study sites had a significant volume of heavy vehicles; hence, it was chosen as a separate variable. A flowchart representing the step by step methodology of the study is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the various steps followed during the formulation of the models

Full size image

Construction of the block diagram of the model

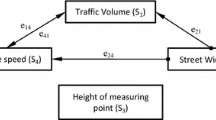
Five roadway sections of different zones were selected for the study. Two were from commercial zones, one was from a silence zone, one was from a residential zone, and one was a mixed residential cum commercial zone. The parameters selected for modeling purposes were arranged in such a way that the interactions between the relevant parameters was indicated using unidirectional and bidirectional arrows. From the literature, as well as the real-life observations, the interactions between the parameters were considered. The block diagram representing the variables of the study and their interactions is shown in Fig. 3. For example, both traffic volume (S1) and traffic speed (S3) interact with each other with higher traffic volumes leading to higher traffic speed and conversely traffic speed affects traffic volume therefore both are connected with the help of a bidirectional connector. The interactions between them is shown as e13 and e31. Traffic volume (S1) can affect the number of horns per hour (S4) but the reverse interaction is not present, hence both the variables are connected with a unidirectional connector and e14 represents the interaction between them. Street width (S2) can affect the number of vehicles per hour (S1) with narrow street leading to lesser traffic volume and wider streets leading to higher traffic volumes. The reverse interaction is not present hence both these variables are connected with a unidirectional connector and e21 represents the interaction between them. Street width (S2) can affect the number of horn (S4) events reported in a given interval of time, with wider streets often reporting more honking due to higher traffic volumes. The reverse interaction is not feasible and hence both the variables have been connected with a unidirectional connector and e24 represents the interaction between them. Wider streets often lead to higher traffic speeds and narrower streets leading to lower traffic speeds, this is why street width (S2) and traffic speed (S3) have been connected with a unidirectional connector with e23 representing the interaction between them. The number of heavy vehicles does not affect any of the variables and as such the variable was not connected with any other variable.

Fig. 3
figure 3

Block diagram representing the model parameters along with the interactions

Full size image

Data collection

All five selected sites were initially surveyed for one week to select the morning, afternoon, and evening rush hours. The selection of the time periods was done in order to develop models for the worst case scenario of traffic noise levels. Data collection was performed for three months, from Oct to Dec 2019. Traffic volumes were obtained through video recordings, and average speed was also obtained from video graphic measurements by marking an initial distance of 50 m over the road surface. Time taken to cross the markings was obtained from the video timer. Knowing both distance and time, speed was calculated. The number of horns blown per hour was also obtained from the video recordings. Traffic noise levels were measured using a Casella CEL-633C class 1 sound level meter, which was calibrated using a Casella CEL-120/1 class 1 acoustic calibrator. The measurements were made as per ISO 1996-1 (ISO 2003). Noise descriptors Leq,1h dB(A), L10,1h dB(A), and L90,1h dB(A) were selected as the relevant noise parameters. Their values were directly obtained from the sound level meter software.

Development of PFM for study sites

For the development of PFM, there is a need to assign weights to the main parameters considered in the study, represented along the diagonal of the PFM, and assign weights to the interaction terms. The data of 3 months’ duration were averaged and then used for assigning the weights. The data for the three rush hours of each site is given below Table 1, Table 2, and Table 3. The variable with the highest value was assigned a weight of 5, and one with the lowest value was assigned a weight of 1 (Nigel Cross 2000). For all the remaining three values, interpolation was used to assign the weights.

Table 1 Average values for morning rush hour (9:30 am to 10:30 am) data collected from Oct to Dec 2019
Full size table
Table 2 Average values for afternoon rush hour (12:30 pm to 1:30 pm) data collected from Oct to Dec 2019
Full size table
Table 3. Average values for evening rush hour (4:30 pm to 5:30 pm) data collected from Oct to Dec 2019
Full size table

For morning rush hour, traffic volume per hour ranged from 243 to 519. Thus, a weighting of 5 is assigned to the main chowk site, and a weighting of 1 is given to the old town road. The number of heavy vehicles ranged from 2 to 107, and thus a weight of 1 is assigned to the hospital road, and a weight of 5 is assigned to the old town road. The average speed values ranged from 18.4 to 38.2 kmph. Hence, 1 is assigned to hospital road, and 5 is assigned to the old town road. The width of road pavements ranged from (4.9 to 6.2) m, so weights of 1 and 5 are assigned to old town road and azad gunj road, respectively. A similar approach is applied while assigning the weights for the other two rush hours.

The values of interactions are based on logical reasoning and correlational analysis (Nicol and Wilson 2004). As traffic volume and average speed are strongly related, a weight of 4 is assigned to their interaction. The relation with other parameters is nonexistent, and as such, a weight of 1 is assigned to them. Generally, there is a tendency among drivers that they drive at higher speeds if the pavement is of sufficient width thus, a weight of 3 has been assigned to their interaction. Street width and the number of heavy vehicles may be related to some extent, so 2 is given to their interaction. Street width is strongly related to traffic volume, hence the weight of 4 is assigned. Street width is also related to traffic speed moderately; therefore, the weight of 3 has been given. Street width is not associated with the number of horns, and as such, a weight of 1 has been assigned. The speed of the vehicle is strongly related to traffic volume; hence, the weight of 4 has been set. A nonexistent relation was considered for all other parameters, and thus a weight of 1 has been assigned. The number of horns is not related to any of the other parameters, and therefore the weight of 1 was set for the interactions. The number of heavy vehicles can affect vehicular speeds. Generally heavy traffic leads to the lowering of traffic stream speed due to the reluctance of other vehicles to perform overtaking maneuvers; however, the relation is not a very strong one and thus a weight of 2 was assigned for their interaction. Interactions with other variables were considered to be nonexistent. Therefore, a value of 1 has been set. The procedure adopted for assigning the weights was taken from Nigel's work (Nigel Cross 2000). The eigenvalue formulation is done as:

$$ \left(A-\lambda I\right)\times {w}^T=0, $$
(2)

where A is the PFM of a given site; I is an identity matrix; λ is the eigenvalue spectrum, wT is the eigenvector's transpose. The solution of Eq. 2 yields (A − λ I) = 0; thus, a spectrum of eigenvalues are obtained. Corresponding to the maximum eigenvalue, the eigenvector is calculated, such that ∑wi = 1. wi is eigenvector used to modify the ith column of PFM. After updating the PFM, the matrix's permanent is calculated, represented as PNI (permanent noise index) from Eq. 1. The initial PFM and the updated PFM for morning rush hour are shown in Table 4. Similarly, PFM’s obtained for afternoon and evening rush hours are shown in Table 5 and Table 6, respectively. The obtained noise parameters including hourly equivalent noise level, Leq, 1h dB(A), background noise level, L90, 1h, dB(A), and maximum noise level, L10, 1h dB(A), are then correlated with the obtained PNI values to check the appropriateness of the PNI as a representation of the overall acoustic environment. The values of the noise parameters and PNI are shown in Table 7.

Table 4 Initial and updated PFM for the morning rush hour (9:30 am to 10:30 am) at the selected sites
Full size table
Table 5 Initial and updated PFM for the afternoon rush hour (12:30 pm to 1:30 pm) at the selected sites
Full size table
Table 6 Initial and updated PFM for the evening rush hour (4:30 pm to 5:30 pm) at the selected sites
Full size table
Table 7 Average values of the PNI and noise indices collected from Oct to Dec 2019
Full size table

Results

The variation of PNI with noise parameters for the three rush hours for the data collected is shown below Fig. 4, Fig. 5, and Fig. 6. The usage of PNI was found to correlate well with all three selected noise parameters. To verify and measure this correlation, Pearson’s correlation coefficient and linear regression was performed between the observed values for the selected noise indices and PNI. The results for the correlation between PNI values and noise levels for the three rush hours are shown in Table 8. A logarithmic transformation was applied for PNI so that uniformity with noise levels is maintained (which are also measured on a logarithmic scale). The results obtained from linear regression are shown in Table 9 and they clearly show a high value of R, R2, and adjusted R2. This means that using the five parameters incorporated in PNI, 92%, 79.5%, and 85.2% of the variance in Leq, 1h values for the morning, afternoon, and evening rush hour can be explained. Variation of 90.7%, 74.2%, and 96% in L10, 1h can be explained using PNI for the morning, afternoon, and evening rush hours, respectively. Variation of 98%, 91%, and 80.6% in L90, 1h can be accounted for, using PNI for the morning, afternoon, and evening rush hours, respectively.

Fig. 4
figure 4

Variation of Leq,1h with PNI for the selected sites during the morning (a), afternoon (b), and evening (c) rush hour

Full size image
Fig 5
figure 5

Variation of L10,1h with PNI for the selected sites during the morning (a), afternoon (b), and evening (c) rush hour

Full size image
Fig 6
figure 6

Variation of L90,1h with PNI for the selected sites during the morning (a), afternoon (b), and

evening (c) rush hour

Full size image
Table 8 Correlation between PNI (Permanent Noise Index) and the noise indices used in the study
Full size table
Table 9 The output of the linear regression for the noise indices (Leq, L10, and L90)
Full size table

Validation of the developed models

To validate the developed models, data collection for the same sites was done for nine months from Jan to Sep 2020. Average values for three months each were used for testing the models. This was done because the data collection for model development was done for three months. The results of the same are shown in Table 10. The results were further evaluated by plotting the measured values against the predicted values as shown in Fig. 7. The R2 values revealed a good agreement between the measured and predicted values.

Table 10 Comparison of measured noise levels and predicted noise levels
Full size table
Fig 7
figure 7

A plot of measured and predicted values of Leq, 1h (a), L90, 1h (b), and L10, 1h (c) as per developed models

Full size image

Usage of other subsystems

In this study, only a single subsystem was used. The addition of more subsystems can be done using the GTA. This involves integrating other subsystems by calculating PNI values for all other subsystems and then forming another PFM using PNI values as the diagonal elements and the interactions of the subsystems as the off-diagonal elements. Such an analysis can result in better predictions.

Discussion

The development of noise models is not a new procedure as far as developed countries are concerned. However, for developing nations like India, more emphasis needs to be given to environmental noise modeling of which traffic noise forms a significant contributor. The study presented a novel and parsimonious procedure for predicting RTN levels. RTN models play a vital role in designing new roads by estimating the expected noise levels and assessing the changes that may occur due to the anticipated changes in any contributing variables over a given period. A systems approach has been adopted in the study. RTN system is comprised of various subsystems like road traffic subsystem, human subsystem, environmental subsystem, traffic network, and urban subsystem.

In the present study, five parameters from the traffic subsystem were considered. These included traffic volume, traffic speed, the volume of heavy vehicles, pavement width, and honking. The inclusion of honking was done because it is the main characteristic of road traffic in developing countries, including India. Besides, some studies have also shown improvements in traffic noise modeling by including honking as a parameter (Kalaiselvi and Ramachandraiah 2016; Sharma et al. 2014; Vijay et al. 2014, 2015). All the variables were incorporated in a matrix form by assigning the weights to the selected parameters, represented along the matrix's diagonal, and weights were assigned to the variables' interactions, represented by the off-diagonal elements. Assignment of weights for the main parameters was done based on the data collected from the field, and for interactions, the weights were decided based on intuition and established knowledge. As the development of PFM involved human factor, PFM was updated using the eigenvalue formulation, and permanent of the updated matrix, represented as PNI, was calculated. The usage of PNI was validated using graphical analysis. The study's traffic noise parameters were equivalent noise level Leq,1h, and percentile values L10,1h , and L90,1h. Models were developed by performing simple linear regression between noise parameters and PNI values. All the models resulted in a good fit for the collected data. The validity of the models was tested for nine months. The models showed a reasonably good fit, although a decrease in the R2 values was obtained. The models were found to overestimate the noise parameters' values, which ranged from (0.58 to 2.88) dB(A). This shows that the models performed reasonably well over the given period. However, the inclusion of other subsystems can help in the further improvement of the models.

Strengths and limitations

The strengths of the present study can be summarized as:

  • This is the first study performed in the state of Jammu and Kashmir in which the modeling of road traffic noise has been undertaken.

  • As per the author’s knowledge, the application of GTA in RTN prediction has not been undertaken in any of the studies conducted under heterogeneous traffic conditions prevalent in India. Although one study (Singh et al. 2016b) depicting GTA's application was found, it was applied to the data obtained from London, which has different traffic and acoustic environment.

  • The models have been validated from the data collected over nine months from Jan to Sep 2020. This period includes winter, summer, and autumn seasons in Jammu and Kashmir. Given the models were found to have good prediction ability, we can infer that models can be applied for different weather conditions. This is an essential feature of the study as various studies have depicted that traffic noise levels are affected by the prevailing weather conditions, especially temperature (Bueno et al. 2011; Hamad et al. 2017).

  • The inclusion of honking in the developed models also adds to the strengths of the model.

  • The GTA is a new and easy to comprehend approach for noise modeling purpose. The models can prove helpful for future research as well.

The limitations of the study include:

  • Only five parameters from one of the subsystems, i.e., traffic subsystem, have been used for modeling.

  • The inclusion of other subsystems and their parameters is an essential component that influences RTN. The present study has considered only one of the subsystems.

  • Developed models were validated only for the sites from which initial data was taken. The applicability of the models for different sites has not been considered. Thus it needs further investigation.

Future scope of work

The inclusion of more subsystems can refine the study. The applicability of the developed models for sites with different traffic environments needs to be evaluated. The work on these two improvements will be undertaken in a separate study. The procedure for the inclusion of other subsystems has already been mentioned in the previous section.

Conclusion

As per World Health Organization, nearly 1.6 million London inhabitants are exposed to noise levels > 55dB(A) every day, which is more than the upper limit responsible for causing severe health issues (Halonen et al. 2015). Given that resource availability in developed countries is much larger than available in developing countries, it becomes imperative for the relevant authorities in developing countries to adopt a more scientific approach while designing the new areas or redesigning the existing infrastructure. Although attention has been given to most of the environmental pollutants, noise pollution remains unattended. In this direction, developing countries need to promote more studies and research. Most developed countries have formulated their traffic noise models, but developing countries have been utilizing either the models used in developed countries or introducing some modifications as per the local conditions. However, such a practice is not feasible everywhere, and as such, studies should be conducted at microlevels. The current study is one such step in this direction. The models developed can be modified to better model the traffic noise levels; however, as an initial step, this can prove beneficial for the authorities in envisaging the current and future acoustical scenarios of the study areas. As per the observed data, noise levels in all the zones exceeded the safer limits set by both international and national regulatory authorities. The study can thus be utilized for testing the various countermeasures as well.