Introduction

Academic interest in the locomotion of aquatic and aerial animals has been renewed recently by the development of nature-inspired robotics. Even if the progress of computational possibilities now allows to simulate these complex fluid-structure interactions efficiently, analytical models are still necessary to bring physical insights into this fascinating field. The present paper is aimed at giving a short introductory survey of these analytical models under a unified approach. Readers interested in this field may want to read recent reviews with alternative approaches [1–6].

Animal locomotion in fluids is usually characterized by the large amplitude flapping of a lifting surface of high flexibility. This propulsion mode which allows for high maneuverability and efficiency will be the focus of the present paper. The discussion will be restricted to the fluid mechanics of locomotion and little will be said about the internal mechanics of the animals which can be found elsewhere (see [7] for instance). We will limit the analysis to animals large enough so that the Reynolds number is asymptotically large and the potential flow theory applies. This happens when the lifting surface is larger than few millimeters with a typical speed of several body lengths per second. In this case, the flow can be considered irrotational, meaning that the flow vorticity is concentrated in thin boundary layers adjacent to the body surface and in a thin wake behind the body.

In the regime of high Reynolds numbers, the biofluiddynamic theories are traditionally divided in two according to the aspect ratio of the lifting surface. For small aspect ratios (elongated animals like eels for instance) slender-body theory is used [8, 9] while for large aspect ratios (lunate tails or most wings) a two-dimensional or lifting-line theory is appropriate [10, 11]. We will see in the following that these theories can be viewed as two asymptotic cases of the more general lifting-surface theory.

Lifting-surface Equation

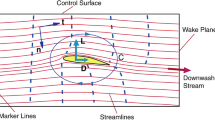
Consider a Cartesian coordinate system (Oxyz) and a uniform, incompressible, inviscid flow of velocity U directed along the Ox-axis. A thin surface S of semi-chord L and semi-span H is moving in this flow at the angular frequency ω around the reference plane z = 0 (see Fig. 1). If this lifting surface is assumed to undergo small displacements and deformations, the problem becomes linear and is equivalent to small periodic disturbances of the incident flow. Adopting the complex notation with an implicit factor eiωt for all quantities, the motion of S prescribes a perturbation \(\emph{w}(x,y)\) of the flow velocity in the z-direction

$$ \emph{w}(x,y)= D\, z(x,y)\; \mbox{on $S$}, \quad \mbox{with} \quad D=\left(\mathrm{i}\omega +U\partial_x \right), \label{eq:kinematicBC} $$
(1)

where D is the material derivative and z(x,y) is the deformation of the plate along the Oz axis. The problem consists of relating \(\emph{w}\) to the perturbation pressure jump across the surface S.

Fig. 1
figure 1

Schematic of the lifting-surface problem in the two limiting cases of (a) large aspect-ratio H ≫ L and (b) small aspect-ratio H ≪ L

Full size image

The flow is described by the perturbation potential ϕ which satisfies the Laplace equation with a Neumann boundary condition on S

$$ \Delta \phi =0, \quad \mbox{with}\quad \partial_{z}\phi=\emph{w}(x,y) \;\mbox{on $S$}, $$
(2)

such that the total flow velocity is \(\mathbf{U}+\nabla \phi\). Using the Green’s representation theorem [12], the perturbation potential can be related to the jump of ϕ across the plane z = 0 (the normal velocity being continuous across the horizontal axis)

$$ \phi(\mathbf{R})=\int_{S+\Sigma} [\phi](\mathbf{r}) \partial_{z_S}G(|\mathbf{R}-\mathbf{r}|) \mathrm{d} S, \label{eq:Green_phi} $$
(3)

where

$$[\phi](x,y)=\phi\left(x,y,0^+\right)-\phi(x,y,0^-) $$
(4)

is the potential jump, R is any point of the flow domain, r is any point on the lifting surface S or its wake Σ and G(r) is the Green function of the Laplace equation

$$ G(r)=-\frac{1}{4 \pi r}. $$
(5)

The kinematic boundary condition (1) is imposed by taking the z-derivative of the integral equation (3) and taking the limit as z tends to zero

$$ \emph{w}(x,y)=\times\!\!\!\!\!\!\!\int_{S+\Sigma} [\phi](\mathbf{r}) F(|\mathbf{x}-\mathbf{r}|) \mathrm{d} S, \label{eq:LS} $$
(6)

where x = (x,y) is on S,

$$ F(r)=\frac{1}{4 \pi r^3}, \label{eq:kernel} $$
(7)

and the cross on the integral sign implies that the integral is defined in the finite-part sense as introduced by Hadamard [13] and summarized in the present context by Mangler [14] (the finite-part integral can be viewed as a generalization of the classical Cauchy principal value).

The potential jump [ϕ] when derived with respect to x or y yields the two components of velocity jump across the plate. These two components are also equal or opposite to the x- and y-components of the vorticity distribution γ x and γ y in the plate and its wake

$$ \gamma_x=-\partial_y[\phi], \quad \gamma_y=\partial_x[\phi]. \label{eq:Bernoulli1} $$
(8)

From a physical point of view, the vorticity is formed in the viscous boundary layers attached to the lifting surface and is then advected in the wake by the flow velocity U. This means that, in the wake, [ϕ] and its derivatives are x-periodic with a wavelength λ = 2 πU / ω (see Fig. 2).

Fig. 2
figure 2

Typical vorticity lines in the lifting surface and in its wake in the plane z = 0

Full size image

The pressure jump [p] is obtained through the linearized Bernoulli equation

$$[p] = -\rho D[\phi]. \label{eq:Bernoulli2} $$
(9)

Given the x-periodicity of [ϕ] in the wake, the pressure jump is zero on Σ as expected. Note that the Kutta condition on the trailing edge ([p] = 0) is ensured by Kelvin’s circulation theorem which implies that the vorticity distribution is continuous between S and Σ.

However, no particular boundary condition applies on the leading and side edges of the plates and the least-singular solution leads to a vorticity distribution γ y that goes as x 1/2 and y 1/2 close to these edges. Using equations (8) and (9), the pressure jump is found to be regular at the side edges and singular at the leading edge with the classical x  − 1/2 singularity. This singularity being integrable, it does not lead to infinite forces on the plate and is therefore physically meaningful. The finite thickness of the plate could also been taken into account to smooth out this leading-edge singularity [15].

Equation (6) is known as the lifting-surface integral. Integrating by parts and using the relations (8–9), it can also be expressed in terms of the pressure jump or the vorticity distribution [2, 10, 16, 17]. The lifting-surface integral relates the prescribed perturbation velocity w (called the downwash in airfoil theory) to the unknown potential jump [ϕ] through an integral equation. From a mathematical point of view, this inverse problem is a Fredholm equation of the first kind.

To calculate the pressure forces exerted by the flow on the moving flexible plate, one needs to invert the lifting-surface equation (6) and use the relation (9). Because of the singular nature of the kernel function F(r) defined by equation (7), specific numerical methods have to be used to invert the lifting-surface equation such as the vortex-lattice method [18, 19], the doublet-lattice method [20, 21] or the waving plate method [22]. In the limit of small or large aspect ratios, asymptotic methods can also be used [15]. In the limit H ≪ L, it leads to the slender-body theory and when H ≫ L to the lifting-line theory as detailed below.

Slender-body Theory

Consider a lifting surface of small aspect ratio A = H/L ≪ 1 as depicted in Fig. 1(b). The lifting surface integral equation (6) can be rewritten as

$$ \emph{w}(x,y)=\frac{1}{4 \pi}\times\!\!\!\!\!\!\!\int_{-H}^{H} I(x,\varepsilon)\mathrm{d}\eta, \label {eq:SB_LS} $$
(10)

with

$$ I(x,\varepsilon)=\int_{-l}^{\infty} [\phi](\xi,\eta) \frac{\mathrm{d}\xi}{\left[(x-\xi)^2+\varepsilon^2\right]^{3/2}}, \label{eq:int_SB} $$
(11)

where x = − l(η) is the plate leading edge and ε = y − η is small compared to x.

An expansion of I(x,ε) can be calculated in the limit of small A using the method of Matched Asymptotic Expansion [15]. The principle of this method is to assume an intermediate length δ such that |ε| ≪ δ ≪ L and to separate the integral of equation (11) in two parts: one for |x − ξ| < δ and the other for |x − ξ| > δ. After some calculation, it yields

$$\begin{array}{rcl} I(x,\varepsilon)&=&\frac{2}{\varepsilon^2} [\phi](x,\eta) - \left(\ln \frac{|\varepsilon|}{2 l}+1\right)\partial^2_x[\phi](x,\eta) \\ &&+\times\!\!\!\!\!\!\!\int_{-l}^{\infty} [\phi](\xi,\eta) \frac{\mathrm{d}\xi}{\left| x-\xi\right|^3} + O\left( \varepsilon^2 \ln\frac{|\varepsilon|}{l}\right). \end{array} $$
(12)

Injecting this expansion into equation (10) gives

$$ \emph{w}(x,y)= \frac{1}{4 \pi}\times\!\!\!\!\!\!\!\int_{S+\Sigma} [\phi](\xi,\eta) F_{\mathrm{SB}}(x-\xi,y-\eta) \mathrm{d} \xi \mathrm{d} \eta, \label{eq:LS_SB1} $$
(13)

where

$$ F_{\mathrm{SB}}(x,y)=\frac{2 \delta(x)}{y^2} - \left(\ln \frac{|y|}{2L}+1\right)\delta''(x) + \frac{1}{\left| x\right|^3} + \cdots \label{eq:kern_SB} $$
(14)

with δ(x) the Dirac delta function. Equation (13) is the equivalent of the lifting-surface equation (6) in the limit of small A. The new kernel F SB is now expressed as a generalized polynomial of |y|.

Assuming that the prescribed velocity \(\emph{w}\) only depends on x, the first-order solution is obtained by keeping only the first term of the kernel (14) and inverting equation (13). It yields

$$[\phi_0](x,y)=-2\emph{w}(x)\sqrt{h^2-y^2}, $$
(15)

where h(x) is the local semi-span. The corresponding pressure jump is found using relation (9)

$$[p_0](x,y)=2\rho D\left(\emph{w}(x)\sqrt{h^2-y^2}\right), $$
(16)

and the force exerted on the fluid per unit length is obtained by integrating the pressure jump between − h and h

$$ F_0(x)=D\left(\rho \pi h^2(x) \emph{w}(x)\right). \label{eq:F0} $$
(17)

This classical expression of the slender-body force was found by Lighthill [8] with a different approach. Considering that m(x) = ρπ h 2 is the added mass of fluid per unit length (the fluid contained in a circle whose diameter is the local plate span), the product ????mw is the momentum given to the fluid by the lifting surface. Equation (17) simply expresses that the force on the fluid is the rate of change of this momentum in the fluid reference frame, i.e. \(F_0=D(m\emph{w})\).

The advantage of the present approach is that it can be carried out up to any order in A without difficulty by expanding the potential jump in even powers of A. Injecting such an expansion into equation (13) and inverting the integral equation gives the expression of the corrective potential jump [ϕ 1] at order A 2 smaller than [ϕ 0]. Note that the logarithmic term of order (x  − 3ln y) appearing in equation (14) has to be treated together with the O(x  − 3) term as it is routinely the case when using perturbation methods [15]. The corrective force is calculated by integrating [ϕ 1] between − h and h and applying the operator D. It yields

$$ F_1= D \left(\rho \pi \frac{h^4}{4}\left[\left(\ln \frac{4}{A}-\frac{3}{4}\right)\emph{w}''(x) + \times\!\!\!\!\!\!\!\int_{-L}^{\infty} \frac{\emph{w}(\xi)\mathrm{d}\xi}{\left| x-\xi\right|^3} \right]\right), $$
(18)

where a periodic velocity is assumed in the wake such that \(\emph{w}(x)=\emph{w}(L)\exp[\mathrm{i}\omega(L-x)/U]\) for x > L. The total force on the fluid is

$$ F(x)=F_0+F_1+O\left(\rho h^2\emph{w}\,A^4\ln A\right). $$
(19)

It can be noted that the corrective force F 1 is (A 2ln A) smaller than F 0 as expected. When the imposed velocity w(x) is known, this correction can be computed easily.

To our knowledge, perturbation methods have never been applied to the problem of slender-body swimming and the result above is therefore new. In the limit of large aspect ratio however, this approach have been used to justify and generalize the lifting-line theory as exposed below [10, 11].

Lifting-line Theory

Consider now a lifting surface of large aspect ratio A = H/L as depicted in Fig. 1(a). We shall assume that the reduced frequency k = Lω/U is of order unity which prevents the use of any quasi-steady approximation. Note that the Strouhal number based on the chord 2 L is St = Lω/(πU) = k/π and therefore k ≈ 1 corresponds to St ≈ 0.3, close to the values observed in animal locomotion.

Following the procedure used in the slender-body theory but inverting x and y, the lifting-surface integral reduces to

$$ \emph{w}(x,y)= \frac{1}{4 \pi}\times\!\!\!\!\!\!\!\int_{S+\Sigma} [\phi](\xi,\eta) F_{\mathrm{LL}}(x-\xi,y-\eta) \mathrm{d} \xi \mathrm{d} \eta, \label{eq:LS_LL1} $$
(20)

where the kernel in the limit of large A is

$$ F_{\mathrm{LL}}(x,y)=\frac{2 \delta(y)}{x^2} - \left(\ln \frac{|x|}{2H}+1\right)\delta''(y) + \frac{1}{\left| y\right|^3} + \cdots \label{eq:kern_LL} $$
(21)

Keeping only the first-order term in equation (21) and integrating by parts equation (20) yields the classical two-dimensional integral equation

$$ \emph{w}(x,y)= \ -\!\!\!\!\!\!\int_{-l(y)}^{\infty} \frac{\gamma_y(\xi,y)\mathrm{d} \xi}{2 \pi(\xi-x)}, \label{eq:LS_2D} $$
(22)

where the integrand expresses the azimuthal velocity induced in x by a point-vortex of circulation γ y d ξ located in ξ. Note that the boundary terms disappear from the integration by parts because they are infinite at the leading edge and vanishing as x→ ∞ (this is a particular property of the finite-part integrals [14]). Here the finite-part integral reduces to the Cauchy principal value (noted with a bar on the integral sign). The integral equation (22) is two-dimensional in the sense that, for each value of y, it can be treated independently as a local two-dimensional problem.

The inverse problem (22) is a classical problem of unsteady airfoil theory [3, 11, 23]. Its solution in terms of the pressure jump is found by inverting equation (22) and using the relations (8, 9)

$$[p_{\mathrm{2D}}](x,y)=\frac{2\rho U}{\pi l} \sqrt{\frac{l-x}{l+x}} \ -\!\!\!\!\!\!\int_{-l(y)}^{l(y)} \Lambda(x,\xi)\emph{w}(\xi,y)\mathrm{d} \xi, \label{eq:2D_pressure} $$
(23)

where x = ±l(y) correspond to the leading and trailing edges of the lifting surface,

$$\begin{array}{rcl} \Lambda(x,\xi) &=&\sqrt{\frac{l+\xi}{l-\xi}}\left[C\left(\frac{kl}{L}\right)-1+\frac{l}{\xi-x}\right] \\ &&+\frac{\mathrm{i}k}{2}\ln\left(\frac{l^2-x\xi+\sqrt{l^2-\xi^2}\sqrt{l^2-x^2}} {l^2-x\xi-\sqrt{l^2-\xi^2}\sqrt{l^2-x^2}}\right), \end{array} $$
(24)

and C(k) is the Theodorsen function [24]

$$ C(k)=\frac{H_1^{(2)}(k)}{H_1^{(2)}(k)+\mathrm{i}H_0^{(2)}(k)}, $$
(25)

with \(H_n^{(2)}\) the Hankel function of the second kind. Examining the kernel given in equation (21), the two-dimensional pressure jump equation (23) appears to be valid up to a O(A  − 2ln A) corrective term. It is out of the scope of the present paper to calculate this correction in details but the readers have to bear in mind that its order is strongly dependent on the hypothesis made.

One important point is that the kernel given by equation (21) is not pertinent in general because x cannot be considered small compared to H in the far wake. It can be shown [10] that, for small frequencies (i.e. k ≪ 1), the two-dimensional approach equation (23) is valid up to a correction of order A  − 1 like in steady lifting-line theory. If the reduced frequency k is of order unity or higher as it is the case in animal locomotion in general, the potential jump in the wake is a fast oscillating function with a period λ = o(H). Thus, under this particular hypothesis, the far wake do not contribute to the integral equation (20) and the kernel given by equation (21) is relevant.

The other limitation of the present asymptotic approach is that the angle between the leading edge and the Oy-axis must remain small everywhere (at most O(A  − 1)). This is because the leading edge x = − l(y) have to be a function varying on the typical length of order H in order to avoid boundary terms when integrating by parts equation (20). This restricts the analysis to surfaces with cusped tips as discussed by Van Dyke [16] in the steady case. For rounded tips (semi-elliptical wings for instance) or if the leading-edge is inclined to the flow, the two-dimensional theory is valid up to a O(A  − 1ln A) term as proved by Guermond and Sellier [10]. Note that, in the particular case of a rectangular lifting surface, the problem can be simplified by taking its Fourier transform along x as it has been shown in [25, 26].

Discussion

In this paper, potential flow models derived from unsteady airfoil theory have been presented with a unified approach in the context of aquatic and aerial locomotion. It has been shown that, in the general case, the lifting-surface equation applies whose inherently singular nature imposes specific numerical methods to be inverted. However, the lifting-surface equation can be simplified in two asymptotic cases: in the limit of a lifting surface of small aspect ratio, it leads to the slender-body theory while in the large aspect ratio limit, a two-dimensional or lifting-line theory is appropriate.

For the sake of simplicity, the lifting-surface theory has been presented in the linear limit, i.e. for small displacements and deformations of the plate. Equation (3) being valid for large displacements when the surface of integration is taken on the moving surface, the present formulation could be generalized to arbitrarily large displacements using the same steps. In the slender-body and two-dimensional limits, this large-amplitude theory have been developed by Lighthill [9] and Wu [6] respectively.

We have demonstrated that the slender-body and the two-dimensional theories are valid up to an order (A 2ln A) and (A  − 2ln A) respectively, where A is the aspect ratio of the lifting surface. In the two-dimensional case, this scaling is valid only for surfaces with cusped tips and a leading edge almost perpendicular to the flow. For curved or swept surfaces or for surfaces with rounded tips, the correction is larger, of order (A  − 1ln A).

The lifting surface has been assumed infinitely thin here, whereas, in natural locomotion, the surface thickness is usually non-negligible. This can be taken into account by using the linear property of the potential flow theory. The potential of a thick lifting surface is simply the sum of the potential due to the thickness alone (the surface being motionless and aligned to the flow) and the potential due to motion alone (calculated in the present paper for an infinitely thin surface). Since the pressure jump is linearly dependent on the potential jump, the forces exerted on the lifting surface by the fluid can also be decomposed in the same manner.

The analytical models introduced here are restricted to small displacements and deformations (linearity), inviscid flow and asymptotically large or small aspect ratios. These limitations can be viewed as weaknesses but the inherent simplicity of these models allows to gain physical insights into the fundamental fluid mechanics of animal locomotion. Besides, the analytical character of these models make them perfect candidates for optimization or control procedures as they allow for fast calculations. The additional effects of viscosity, non-linearity and aspect-ratio can be treated separately with experiments or detailed numerical calculations.