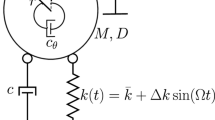Skip to main content
SpringerLink
Log in

Experimental Investigation of Dynamics and Bifurcations of an Impacting Spherical Pendulum

  • Published:
Experimental Mechanics Aims and scope Submit manuscript

Abstract

Since Newton first considered the motion of a spherical pendulum over 200 years ago, many researchers have studied its dynamic response under a variety of conditions. The characteristic of the problem that has invited so much investigation was that a spherical pendulum paradigms much more complex phenomena. Understanding the response of a paradigm gives an almost multiplicative effect in the understanding of other phenomena that can be modeled as a variant of the paradigm. The spherical pendulum has been used to damp irregular motion in helicopters and on space stations as well as for many other applications. In this study an inverted impacting spherical pendulum with large deflection was investigated. The model was designed to approximate an ideal pendulum, with the pendulum bob contributing the vast majority of the mass moment of inertia of the system. Two types of bearing mechanisms and tracking devices were designed for the system, one of which had low damping coefficient and the other with a relatively high damping coefficient. An experimental investigation was performed to determine the dynamics of an inverted, impacting spherical pendulum with large deflection and vertical parametric forcing. The pendulum system was studied with nine different bobs and two different base configurations. During the experiments, the frequency of the excitation remained between 24.6 and 24.9 Hz. It was found that sustained conical motions did not naturally occur. The spherical pendulum system was analyzed to determine under what conditions the onset of Type I response (a repetitive motion in which the pendulum bob does not traverse through the apex. The bob strikes the same general area of the restraint without striking the opposite side of the restraint.), sustainable Type II response (this is the repetitive motion in which the pendulum bob traverses through the apex. The bob strikes opposite sides of the restraint.), and mixed mode response (motion in which the pendulum bob randomly strikes either the same area of the restrain or the opposite side of the restraint) occurred.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Abbreviations

a :

Amplitude of base displacement

C :

Coulomb damping coefficient

g :

Gravitational acceleration

L :

Length of pendulum

M d :

Dynamic mass = M s + M r/2

M r :

Mass of pendulum rod

M s :

Mass of spherical pendulum bob

Ω :

Frequency of base displacement

ϕ :

Latitudinal angular displacement

R :

Coefficient of Restitution

r b :

Radius of bearing

r r :

Radius of pendulum rod

r s :

Radius of spherical pendulum bob

θ :

Longitudinal angular displacement

References

  1. Salam FMA, Sastry SS (1985) Dynamics of the forced Josephson junction: the regions of chaos. IEEE Trans Circuits Syst 328:784–796. doi:10.1109/TCS.1985.1085790.

    Article  MATH  MathSciNet  Google Scholar 

  2. Lee WK (1988) A global analysis of a forced spring pendulum system. Ph.D. Dissertation, University of California, Berkeley

  3. Nayfeh AH, Mook DT, Marshall LR (1973) Nonlinear coupling of pitch and roll modes in ship motions. J Hydrodynam 74:145–152.

    Google Scholar 

  4. Mustafa G (1987) Three-dimensional rocking and topping of block-like structures on rigid foundation. M.S. Thesis, Texas Tech University, Lubbock, Texas

  5. Crossley FRE, Conn NH (1953) The forced oscillation of the centrifugal pendulum with wide angles. J Appl Mech 75:41–47.

    Google Scholar 

  6. Eugene S (1961) On the parametric excitation of pendulum type vibration absorber. J Appl Mech 330–334

  7. Struble RA (1963) Oscillations of a pendulum under parametric excitation. Q Appl Math 212:121–131.

    MathSciNet  Google Scholar 

  8. Mustafa G, Ertas A (1995) Experimental evidence of quasi-periodicity and its breakdown in the column-pendulum oscillator. J Dyn Syst Meas Control 1172:218–225. doi:10.1115/1.2835182.

    Article  MATH  Google Scholar 

  9. Mustafa G, Ertas A (1995) Dynamics and bifurcations of coupled column-pendulum oscillator. J Sound Vib 1823:393–413. doi:10.1006/jsvi.1995.0207.

    Article  MathSciNet  Google Scholar 

  10. Ekwaro-Osire S, Ertas A (1995) Response statistics of a beam-mass oscillator under combined harmonic and random excitation. J Vib Control 12:225–247. doi:10.1177/107754639500100206.

    Article  Google Scholar 

  11. Cuvalci O, Ertas A (1996) Pendulum as vibration absorber for flexible structures: experiments and theory. J Vib Acoust 118:1–9.

    Article  Google Scholar 

  12. Cuvalci O, Ertas A, Cicek I, Ekwaro-Osire S (2002) Nonlinear vibration absorber for a system under sinusoidal and random excitation: experiments. J Sound Vib 2944:701–718. doi:10.1006/jsvi.2001.3836.

    Article  Google Scholar 

  13. Cicek I, Ertas A (2002) Experimental investigation of beam-tip mass and pendulum system under random excitation. Mech Syst Signal Process 166:1059–1072. doi:10.1006/mssp.2001.1475.

    Article  Google Scholar 

  14. Cajori F (1947) Sir Isaac Newton’s mathematical principles on natural philosophy and his system of the world. University of California Press, Berkeley.

    Google Scholar 

  15. Miles J (1979) On the dumped oscillations of a weakly nonlinear pendulum. J Appl Mech 46:213

    MATH  Google Scholar 

  16. Tselman FK (1972) Resonance in small oscillations of the spherical pendulum. Sov Phys Dokl 171:37–38.

    Google Scholar 

  17. Peters RD (1988) Chaotic motion from support constraints of a nondriven rigid spherical pendulum. Phys Rev A 3810:5352–5359. doi:10.1103/PhysRevA.38.5352.

    Article  Google Scholar 

  18. Livesey DL (1987) The precession of simple pendulum orbits. Am J Phys 557:618–621. doi:10.1119/1.15075.

    Article  Google Scholar 

  19. Lowenstern MA (1932) The stabilization effect of imposed oscillations on a dynamical system. Philos Mag 13:458–486.

    MATH  Google Scholar 

  20. Hemp GW, Sethna PR (1964) The effect of high frequency on the motion of a spherical pendulum. J Appl Mech 31:351–354.

    Google Scholar 

  21. Moran TJ (1970) Transient motions in dynamical systems with high frequency parametric excitation. Int J Non-linear Mech 5:633–644. doi:10.1016/0020-7462(70)90053-3.

    Article  MATH  Google Scholar 

  22. Shaw SW, Rand RH (1989) The transition to chaos in a simple mechanical system. Int J Non-linear Mech 241:41–56. doi:10.1016/0020-7462(89)90010-3.

    Article  MATH  MathSciNet  Google Scholar 

  23. Shaw J, Shaw SW (1989) The onset of chaos in a two degree of freedom impacting system. J Appl Mech 56:168–174.

    Article  MATH  Google Scholar 

  24. Moore DB, Shaw SW (1990) The experimental response of an impacting pendulum system. Int J Non-linear Mech 251:1–16. doi:10.1016/0020-7462(90)90034-7.

    Article  Google Scholar 

  25. Dongping J, Haiyan H, Bishop RS (2003) Piecewise analysis of oblique vibro-impacting systems. Acta Mech Sin 196:579–584.

    Article  Google Scholar 

  26. Namachchivaya SN, Jun H, Park HJ (2005) Stochastic dynamics of impact oscillators. J Appl Mech 726:862–870. doi:10.1115/1.2041660.

    Article  MATH  MathSciNet  Google Scholar 

  27. Lenci S (2006) Asymptotic analysis of chattering oscillations for an impacting inverted pendulum. J Appl Math Mech 593:419–434. doi:10.1093/qjmam/hbl009.

    Article  MATH  MathSciNet  Google Scholar 

  28. Mann BP, Carter RE, Hazra SS (2007) Experimental study of an impact oscillator with viscoelastic and Hertzian contact. Int J Non-linear Mech 503:587–596.

    MATH  Google Scholar 

  29. Garza S (1993) Theoretical and experimental investigation of the dynamics and bifurcations of an impacting spherical pendulum with large deflection. Ph.D. Dissertation, Texas Tech University, Lubbock, Texas

  30. Moon FC (1992) Chaotic and fractal dynamics. Wiley, New York, NY, p 336.

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Texas Tech University, Lubbock, TX, 79409, USA

    A. Ertas & S. Garza

Authors
  1. A. Ertas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Garza
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Ertas.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ertas, A., Garza, S. Experimental Investigation of Dynamics and Bifurcations of an Impacting Spherical Pendulum. Exp Mech 49, 653–662 (2009). https://doi.org/10.1007/s11340-008-9182-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11340-008-9182-9

Keywords

Search

Navigation