On the Likelihood Ratio Tests in Bivariate ACDE Models

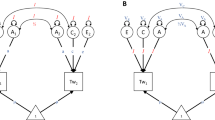
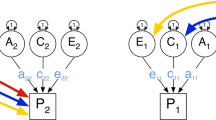
Abstract

The ACE and ADE models have been heavily exploited in twin studies to identify the genetic and environmental components in phenotypes. However, the validity of the likelihood ratio test (LRT) of the existence of a variance component, a key step in the use of such models, has been doubted because the true values of the parameters lie on the boundary of the parameter space of the alternative model for such tests, violating a regularity condition required for a LRT (e.g., Carey in Behav. Genet. 35:653–665, 2005; Visscher in Twin Res. Hum. Genet. 9:490–495, 2006). Dominicus, Skrondal, Gjessing, Pedersen, and Palmgren (Behav. Genet. 36:331–340, 2006) solve the problem of testing univariate components in ACDE models. Our current work as presented in this paper resolves the issue of LRTs in bivariate ACDE models by exploiting the theoretical frameworks of inequality constrained LRTs based on cone approximations. Our derivation shows that the asymptotic sampling distribution of the test statistic for testing a single bivariate component in an ACE or ADE model is a mixture of χ ² distributions of degrees of freedom (dfs) ranging from 0 to 3, and that for testing both the A and C (or D) components is one of dfs ranging from 0 to 6. These correct distributions are stochastically smaller than the χ ² distributions in traditional LRTs and therefore LRTs based on these distributions are more powerful than those used naively. Formulas for calculating the weights are derived and the sampling distributions are confirmed by simulation studies. Several invariance properties for normal data (at most) missing by person are also proved. Potential generalizations of this work are also discussed.

Appendices

Appendix A. Some Properties of the $\bar{\chi}^{2}$ Distribution

Property 1

When the approximating cone $\mathcal {C}_{0}$ of Θ ₀ is a subset of the largest linear² subspace of the approximating cone $\mathcal {C}_{1}$ of Θ ₁ and both cones are convex, the statistic T has an asymptotic $\bar{\chi}^{2}$ distribution. See Dr. Alexander Shapiro’s website for his proof.³ For the special case of $\varTheta_{0}=\mathcal {C}_{0}=\mathbf {0}$, we denote the weight w _k of $\chi^{2}_{k}$ by $w_{k}(p,\mathcal {I}({\boldsymbol {\theta }}_{0})^{-1},\mathcal {C}_{1})$, where p is the dimension of Θ ₁ and $\mathcal {I}({\boldsymbol {\theta }}_{0})$ is the FIM of the alternative model.

Property 2

If nuisance parameters ξ are present but are not on their boundary, when testing ψ=0 against a constrained alternative ψ∈Ψ, the equation for the weights of the $\bar{\chi}^{2}$ distribution is given by $w_{k}=w_{k}(q,\mathcal {I}^{\boldsymbol {\psi }\boldsymbol {\psi }},\mathcal {C})$, where q is the length of ψ, $\mathcal {I}^{\boldsymbol {\psi }\boldsymbol {\psi }}$ is the block of $\mathcal {I}^{-1}$ that corresponds to ψ, and $\mathcal {C}$ is the approximating cone to Ψ in ℝ^q.

Property 3

The weights {w _k } for odd and even k sum up to 0.5, respectively (Shapiro 1987). See Dr. Alexander Shapiro’s website for proofs he receives from correspondence.⁴

Property 4

$w_{k}(p,\mathcal {I}^{-1},\mathcal {C})=w_{p-k}(p,\mathcal {I}^{-1},\mathcal {C}^{0})$, where $\mathcal {C}^{0}$ is the polar cone of $\mathcal {C}$, defined as the subset of ℝ^p whose projection onto $\mathcal {C}$ is the apex of $\mathcal {C}$, or $\mathcal {C}^{0}=\{{\boldsymbol {x}}|{\boldsymbol {x}}'\mathcal {I}\boldsymbol {y}\leq0, \forall \boldsymbol {y}\in \mathcal {C}\}$.

For more properties of the weights of a $\bar{\chi}^{2}$ distribution, see Silvapulle and Sen (2005, Section 3.6).

Appendix B. The Fisher Information Matrix

We derive the FIM $\mathcal {I}({\boldsymbol {\theta }}_{0})$ of a p-variate ACE model with complete normal data. In general, the typical element of the FIM of a covariance structure model is given by $(\mathcal {I})_{\alpha\beta}= \frac{1}{2}\mathrm {tr}\{\Delta_{\alpha} \boldsymbol {\varSigma }^{-1}\Delta_{\beta} \boldsymbol {\varSigma }^{-1}\}$, where Σ=Σ(θ) is the covariance structure and Δ _α =∂ Σ/∂θ _α . For the DZ twin group in an ACE model, $\boldsymbol {\varSigma }^{-1}_{\mathrm {DZ}}$ takes the shape , where all blocks are symmetric. If we define the p×p binary matrix K _ij =∂ C/∂c _ij (e.g., for p=2), we have and the derivatives w.r.t. A and E can be obtained similarly. If we further define K as the p ²×p(p+1)/2 matrix whose columns are the vecK _ij ’s (e.g., K=diag{1,1 _2×1,1} for p=2) and $\mathbf {Q}^{\mathrm {DZ}}_{1}=\mathbf {K}'(\boldsymbol {\varSigma }^{\mathrm {DZ}}_{1}\otimes \boldsymbol {\varSigma }^{\mathrm {DZ}}_{1}+\boldsymbol {\varSigma }^{\mathrm {DZ}}_{2}\otimes \boldsymbol {\varSigma }^{\mathrm {DZ}}_{2})\mathbf {K}$ and $\mathbf {Q}^{\mathrm {DZ}}_{2}=\mathbf {K}'(\boldsymbol {\varSigma }^{\mathrm {DZ}}_{1}\otimes \boldsymbol {\varSigma }^{\mathrm {DZ}}_{2}+\boldsymbol {\varSigma }^{\mathrm {DZ}}_{2}\otimes \boldsymbol {\varSigma }^{\mathrm {DZ}}_{1})\mathbf {K}$, the FIM for the DZ twins can be expressed as

$$ \mathcal {I}^\mathrm {DZ}=\left ( \begin{array}{c@{\quad}cc@{\quad}c} 1+w_\mathrm{A}^2 & 1+w_\mathrm{A}w_\mathrm{C}& 1 \\ 1+w_\mathrm{A}w_\mathrm{C}& 1+w_\mathrm{C}^2 & 1 \\ 1 & 1 & 1 \\ \end{array} \right )\otimes \mathbf {Q}^\mathrm {DZ}_1+ \left ( \begin{array}{cc@{\quad}cc@{\quad}c} 2w_\mathrm{A}& w_\mathrm{A}+w_\mathrm{C}& w_\mathrm{A}\\ w_\mathrm{A}+w_\mathrm{C}& 2w_\mathrm{C}& w_\mathrm{C}\\ w_\mathrm{A}& w_\mathrm{C}& 0 \\ \end{array} \right )\otimes \mathbf {Q}^\mathrm {DZ}_{2}. $$

The FIM $\mathcal {I}^{\mathrm {MZ}}$ for the MZ twins can be obtained similarly by altering the weights. Let α _MZ and α _DZ be sample size proportions of the two types of twin, with α _MZ+α _DZ=1. The overall FIM (of sample size one) is given by $\mathcal {I}=\alpha_{\mathrm {MZ}}\mathcal {I}^{\mathrm {MZ}}+\alpha_{\mathrm {DZ}}\mathcal {I}^{\mathrm {DZ}}$.

A special case of interest is when $\boldsymbol {\varSigma }_{1}^{\mathrm {MZ}}=a_{1}\mathbf {X}$, $\boldsymbol {\varSigma }_{2}^{\mathrm {MZ}}=a_{2}\mathbf {X}$, $\boldsymbol {\varSigma }_{1}^{\mathrm {DZ}}=a_{3}\mathbf {X}$ and $\boldsymbol {\varSigma }_{2}^{\mathrm {DZ}}=a_{4}\mathbf {X}$ are scalar multiples of the same matrix X. In this case, $\mathbf {Q}_{1}^{\mathrm {MZ}}$, $\mathbf {Q}_{1}^{\mathrm {DZ}}$, $\mathbf {Q}_{2}^{\mathrm {MZ}}$ and $\mathbf {Q}_{2}^{\mathrm {DZ}}$ are all scalar multiples of K′(X⊗X)K, so the FIM takes the shape $\mathcal {I}=\mathbf {Y}\otimes [\mathbf {K}'(\mathbf {X}\otimes \mathbf {X})\mathbf {K}]$, where Y is some 3×3 matrix. When A=C=0, we have a ₁=a ₃=1, a ₂=a ₄=0 and X=E ⁻¹, and the FIM becomes

$$ \mathcal {I}=\bigl(\mathbf {1}_{3\times3}+\alpha_\mathrm {DZ}w_\mathrm {DZ}w_\mathrm {DZ}'+\alpha_\mathrm {MZ}w_\mathrm {MZ}w_\mathrm {MZ}'\bigr)\otimes\bigl\{ \mathbf {K}'(\mathbf {E}\otimes \mathbf {E})^{-1}\mathbf {K}\bigr\}, $$

(B.1)

where 1 _3×3 is a 3×3 matrix of 1’s, w _DZ=(w _A,w _C,0)′ and w _MZ=(1,1,0)′.

When data are missing by person, variables related to one twin are missing or present together. The covariance matrix of variables for the singletons is Σ ₀=A+C+E for both MZ and DZ twins, and the FIM for the singletons is given by $\mathcal {I}^{0}=\frac{1}{2}(\mathbf {1}_{3\times 3})\otimes[\mathbf {K}'(\boldsymbol {\varSigma }_{0}\otimes \boldsymbol {\varSigma }_{0})^{-1}\mathbf {K}]$. The FIM for the entire data set is the weighted sum of $\mathcal {I}^{0}$ and the complete data FIM given earlier. Especially, when A=C=0, we have Σ ₀=E, and $\mathcal {I}^{0}=\frac{1}{2}(\mathbf {1}_{3\times3})\otimes [\mathbf {K}'(\mathbf {E}\otimes \mathbf {E})^{-1}\mathbf {K}]$. Summing over the twin and singleton groups, we have

$$ \mathcal {I}=\biggl\{\biggl(\alpha+\frac{1}{2}\beta\biggr)\mathbf {1}_{3\times3}+\alpha_\mathrm {DZ}w_\mathrm {DZ}w_\mathrm {DZ}'+\alpha_\mathrm {MZ}w_\mathrm {MZ}w_\mathrm {MZ}'\biggr\}\otimes\bigl\{ \mathbf {K}'(\mathbf {E}\otimes \mathbf {E})^{-1}\mathbf {K}\bigr\}, $$

where α=α _DZ+α _MZ are proportions of complete twin data and β is the proportion of data with only a single twin.

Appendix C. Lemmas and Proofs

Lemma 1

Let Ω={r|r′Q r<1,r ₁>0,r ₂>0}, where $\mathbf {Q}={a_{1}\ a_{3}\choose a_{3}\ a_{2}}\geq \mathbf {0}$ and r=(r ₁,r ₂)′. Denote $\tau =a_{3}/\sqrt{a_{1}a_{2}}$ and t=arccosτ. We have

$$ \int_\varOmega r_1^2r_2^2\,d {\boldsymbol {r}}=\frac{t-3\tau\sin t+2t\tau^2}{48\sin^5t(a_1a_2)^{3/2}}, \qquad \int_\varOmega r_1r_2^2\,d{\boldsymbol {r}}=\frac{1}{15(1+\tau)^2a_1a_2^{3/2}}, $$

Proof

One only need to prove for the case of a ₁=a ₂=1 and a ₃=τ. This can be done through integration with the reparametrization (r ₁,r ₂)=Rsin(t/2±θ)/sint. The region Ω becomes {0≤R≤1,|θ|≤t/2} under the new coordinate system. □

Lemma 2

The matrices K=diag{1,1 _2×1,1}, $\mathbf {B}=\mathrm {diag}\{1, \frac{1}{2}\times \mathbf {1}_{2\times1},1\}$ and $\mathbf {M}=\mathbf {K}\mathbf {B}'= \mathrm {diag}\{1,\frac{1}{2}\mathbf {1}_{2\times2},1\}$ satisfies

• 1. K′B=I, K′M=K′ and MB=B;

• 2. M is exchangeable with X⊗X for arbitrary X;

• 3. {K′(X⊗X)⁻¹ K}⁻¹=B′(X⊗X)B for arbitrary X.

Proof

See Gupta and Nagar (1999, Section 1.2) or check by simple algebra. □

Proof of Proposition 1

Given the relationship between the two sets of parameters, following the calculations in Appendix B, we have $\tilde{\boldsymbol {\varSigma }}_{i}^{j}=\mathbf {X}^{-1}\boldsymbol {\varSigma }_{i}^{j}\mathbf {X}^{-1\,\prime}$ and $\tilde{\mathbf {Q}}_{i}^{j}=\mathbf {Y}\mathbf {Q}_{i}^{j}\mathbf {Y}'$ for i=1,2 and j=MZ,DZ, where Y=K′(X⊗X)⁻¹ B with K and B defined in Lemma 2 in Appendix C. The relationship between blocks of the FIM can be further found as $\tilde{\mathcal {I}}_{kl}=\mathbf {Y}\mathcal {I}_{kl}\mathbf {Y}'$ for k,l=a,c,e. From Equation (1), we have $\tilde{\mathcal {I}}_{\mathrm{A}}=\mathbf {Y}\mathcal {I}_{\mathrm{A}}\mathbf {Y}'$. For any decomposition $\mathcal {I}_{\mathrm{A}}=\mathbf {L}\mathbf {L}'$, we have $\tilde{\mathcal {I}}_{\mathrm{A}}=\tilde{\mathbf {L}}\tilde{\mathbf {L}}'$, where $\tilde{\mathbf {L}}=\mathbf {Y}\mathbf {L}$, and therefore $\tilde{\mathbf {L}}^{-1}\mathbf {V}\tilde{\mathbf {L}}^{-1\,\prime}=\mathbf {L}^{-1}\mathbf {Y}^{-1}\mathbf {V}\mathbf {Y}^{-1\,\prime} \mathbf {L}^{-1\,\prime}$. From Lemma 2, we have Y ⁻¹=(K′(X⊗X)⁻¹ B)⁻¹=K′(X⊗X)B, and simple algebra gives Y ⁻¹ VY ^−1 ′=|X|² V. Therefore we have $\tilde{\mathbf {L}}^{-1}\mathbf {V}\tilde{\mathbf {L}}^{-1\,\prime}=|\mathbf {X}|^{2}\mathbf {L}^{-1}\mathbf {V}\mathbf {L}^{-1\,\prime}$, which implies $\tilde{\boldsymbol {\varLambda }}=|\mathbf {X}|^{2}\boldsymbol {\varLambda }$, so the weights in the $\bar{\chi}^{2}$ distribution must be the same for the two cases. □

Proof of Corollary 1

The conclusion follows from Proposition 1, if we choose $\mathbf {X}=(\mathbf {C}+\nobreak \mathbf {E})^{-\frac{1}{2}}\mathbf {U}$, where U’s columns are eigenvectors of $(\mathbf {C}+\mathbf {E})^{-\frac{1}{2}}\mathbf {C}(\mathbf {C}+\mathbf {E})^{-\frac{1}{2}}$. Note now both $\tilde{\mathbf {C}}$ and $\tilde{\mathbf {E}}$ are diagonal matrices. Following our calculations in Appendix B, all nine blocks of the FIM must be diagonal and therefore $\mathcal {I}_{\mathrm{A}}$ and L must be diagonal. Simple algebra shows that the eigenvalues −λ ₁,−λ ₂<0<λ ₃ of L ⁻¹ VL ^−1 ′ must satisfy λ ₃=λ ₂ or λ ₃=λ ₁, and the conclusion follows. □

Proof of Corollary 2

From Corollary 1, the pair of true values $\tilde{\mathbf {C}}=\gamma \mathbf {I}/(1+\gamma)$ and $\tilde{\mathbf {E}}=\mathbf {I}/(1+\gamma)$ would yield the same sampling distribution. Because $\tilde{\mathbf {C}}$ and $\tilde{\mathbf {E}}$ are both scalar matrices, as a special case treated in Appendix B, the FIM takes the form $\mathcal {I}=\mathbf {Y}\otimes[\mathbf {K}'\mathbf {I}_{4\times4}\mathbf {K}]=\mathbf {Y}\otimes \mathrm {diag}\{ 1,2,1\}$ for some 3×3 matrix Y, and consequently $\mathcal {I}_{\mathrm{A}}=(\mathcal {I}^{\mathrm{A}\mathrm{A}})^{-1}\propto \mathrm {diag}\{1,2,1\}$. Simple algebra gives λ ₁=λ ₂=λ ₃ and Equations (5) and (6) give $w_{0}=w_{3}=\frac{1}{2}-\frac{\sqrt{2}}{4}$. □

Proof of Proposition 2

From Equation (B.1), , where $\tau^{2}_{\mathrm{A}}=w_{\mathrm{A}}^{2}\alpha_{\mathrm {DZ}}+\alpha_{\mathrm {MZ}}$ and $\tau^{2}_{\mathrm{C}}= w_{\mathrm{C}}^{2}\alpha_{\mathrm {DZ}}+\alpha_{\mathrm {MZ}}$. Consider the decomposition E=X′X and define $\mathbf {B}=\mathrm {diag}\{ 1,\frac{1}{2}\times \mathbf {1}_{2\times1},1\}$, $\mathbf {D}=\mathrm {diag}\{1,\sqrt{2},1\}$, L=K′(X⊗X)⁻¹ BD and $\mathbf {M}=\mathbf {B}\mathbf {D}^{2}\mathbf {B}'=\mathrm {diag}\{1,\frac{1}{2}\mathbf {1}_{2\times2},1\}$. Using Lemma 2, we have the relationship LL′=K′(X⊗X)⁻¹ M(X′⊗X′)⁻¹ K=K′(E⊗E)⁻¹ K. We then consider the transformation $(\bar{{\boldsymbol {a}}}, \bar{{\boldsymbol {c}}})=(\tau_{\mathrm{A}}^{-1}\mathbf {L}'{\boldsymbol {a}},\tau_{\mathrm{C}}^{-1}\mathbf {L}'{\boldsymbol {c}})$. Under the new parametrization, and the quadratic forms defining the cones become $\bar{{\boldsymbol {a}}}'\bar{\mathbf {V}}\bar{{\boldsymbol {a}}}\geq0$ and $\bar{{\boldsymbol {c}}}'\bar{\mathbf {V}}\bar{{\boldsymbol {c}}}\geq0$ with $\bar{\mathbf {V}}=\mathbf {L}^{-1}\mathbf {V}\mathbf {L}^{-1\,\prime}$. Again, remember L ⁻¹=D ⁻¹ K′(X⊗X)B (Lemma 2) and simple algebra gives , so its three eigenvalues must be of the same size. This implies that both Θ _A and Θ _C are circular cones with the height equal to the base radius, and the weights are entirely determined by ρ in $\bar{\mathcal {I}}$. □

Appendix D. Calculation of Weights for Testing Two Components

We derive the weights w _ij using the notations and coordinate systems defined in Section 3.1. Under the elliptic coordinate system, the FIM becomes $\mathbf {G}=\mathbf {J}'\bar{\mathcal {I}}\mathbf {J}$, which is no longer a constant. The unit ball in ℝ⁶ is given by $\mathcal {B}=\{\bar{{\boldsymbol {\theta }}}'\bar{\mathcal {I}}\bar{{\boldsymbol {\theta }}}\leq1\} =\{\alpha_{1}r_{a}^{2}+\alpha_{2}r_{c}^{2}+2\alpha_{3}r_{a}r_{c}\leq1\}$, where the α’s are given in Equation (10).

The polar cone of Θ ₁ was defined in Section 3.1. As a brief proof, we note the inner product between (r _a ,ψ _a ,ϕ _a ,r _c ,ψ _c ,ϕ _c )∈Θ ₁ and $(r^{*}_{a},\psi^{*}_{a},\phi^{*}_{a},r^{*}_{c},\psi^{*}_{c},\phi^{*}_{c})\in\varTheta_{1}^{0}$ is given by

because $\pi/4\leq\phi_{a},\phi^{*}_{a},\phi_{c},\phi^{*}_{c}\leq\pi/2$. The unit ball in ℝ⁶ is given by $\mathcal {B}=\{\bar{{\boldsymbol {\theta }}}^{*\,\prime}\bar{\mathcal {I}}^{-1}\bar{{\boldsymbol {\theta }}}^{*}\leq1\} =\{\alpha^{*}_{1}r_{a}^{*2}+\alpha^{*}_{2}r_{c}^{*2}+2\alpha^{*}_{3}r^{*}_{a}r^{*}_{c}\leq1\}$ in this new coordinate system.

Below we calculate the 10 weights by discretizing the cones. The elliptic cone Θ _A is discretized by S equally spaced angles ψ _s between 0 and 2π, with s=0,1,…,S and ψ ₀=0 and ψ _S =2π. They corresponds to generatrices $\boldsymbol {g}_{s}=(\sqrt {\kappa ^{\mathrm{A}}_{1}}\cos\psi_{s},\sqrt {\kappa ^{\mathrm{A}}_{2}}\sin\psi_{s},\sqrt {\kappa ^{\mathrm{A}}_{3}})'$, which discretizes the circular cone into a polyhedral cone with S faces. Θ _C is similarly discretized with subscripts r=0,1,…,R. The weights will first be calculated using the polyhedral cones and then limits are taken to obtain weights w _ij for the original problem.

4.1 D.1 The Derivation of w ₃₃ and w ₀₀

The region of ℝ⁶ that corresponds to w ₃₃ is simply Θ ₁=Θ _A×Θ _C. Its volume V _∥ inside $\mathcal {B}$ can be calculated by integrating $|\mathbf {G}|^{\frac{1}{2}}=|\mathbf {J}_{\mathrm{A}}||\mathbf {J}_{\mathrm{C}}||\bar{\mathcal {I}}|^{\frac{1}{2}}=|\boldsymbol {\varLambda }_{\mathrm{C}}\boldsymbol {\varLambda }_{\mathrm{A}}|^{-\frac {1}{2}}|\mathcal {I}^{*}_{\mathrm{A}}|^{\frac{1}{2}}r_{a}^{2}r_{c}^{2}\cos\phi_{a}\cos\phi_{c}$ over $\mathcal {B}$.

where the double integral over (r _a ,r _c ) has been simplified using Lemma 1. The weight w ₃₃ is given by w ₃₃=V _∥/V ₆ where V ₆=π ³/6 is the volume of a 6-dimensional ball. w ₀₀ is the proportion of the ball $\mathcal {B}$ that falls into the polar cone. It can be similarly calculated by integrating over $|\mathbf {G}^{*}|^{\frac{1}{2}}=|\mathbf {J}^{*}_{\mathrm{A}}||\mathbf {J}^{*}_{\mathrm{C}}||\bar{\mathcal {I}}|^{-\frac{1}{2}}=|\boldsymbol {\varLambda }_{\mathrm{C}}\boldsymbol {\varLambda }_{\mathrm{A}}|^{\frac{1}{2}}|\mathcal {I}^{*}_{\mathrm{A}}|^{-\frac{1}{2}}r_{a}^{*2}r_{c}^{*2}\cos\phi^{*}_{a}\cos\phi^{*}_{c}$.

4.2 D.2 The Derivation of w ₂₃ and w ₁₀

The region of ℝ⁶ that corresponds to w ₂₃, after projected onto Θ ₁, lies on a face of the discretized Θ _A and the interior of Θ _C. Consider the face of Θ _A, $\mathcal {F}_{s}$, lying between generatrices $\boldsymbol {g}_{s\pm\frac{1}{2}}$. The normal vector to $\mathcal {F}_{s}\times\varTheta_{\mathrm{C}}$ is given by ($\psi^{*}_{a}=\psi_{s}$, $\phi^{*}_{a}=\pi/4$, $r^{*}_{c}=0$). For each s, the proportion of the unit ball $\mathcal {B}$ that falls into this region can be calculated as the product of two proportions: (1) p _⊥(s)=1/2, because the normal vector determines a unidimensional subspace and half of it has the same direction of the normal vector; (2) p _∥(s), the proportion of the 5-dimensional subspace spanned by $\mathcal {F}_{s}\times\varTheta_{\mathrm{C}}$ inside $\mathcal {F}_{s}\times\varTheta_{\mathrm{C}}$.

To calculate p _∥(s), we note that $\mathcal {F}_{s}\times\varTheta_{\mathrm{C}}=\{ \psi_{s-\frac{1}{2}}<\psi_{a}<\psi_{s+\frac{1}{2}}, \phi_{a} =\pi/4, \pi/4<\phi_{c}<\pi /2\}$, so its volume inside $\mathcal {B}$ is given by

where $\widetilde{\mathbf {G}}$ is the 5×5 block of G corresponding to the first, second, fourth, fifth and sixth columns and rows and we have . Note the double integral over $\mathcal {B}$ has been simplified using Lemma 1. We have $w_{23}=\lim \sum_{s}p_{\perp}(s)p_{\parallel}(s)=\frac{1}{2}\lim\sum_{s}V_{\parallel}(s)/V_{5}$, where $V_{5}=\frac{8}{15}\pi^{2}$ is the volume of a 5-dimensional unit ball. The weight w ₁₀ can be obtained by the duality between Θ ₁ and $\varTheta_{1}^{0}$ as given in Property 4 in Appendix A.

4.3 D.3 The Derivation of w ₁₃ and w ₂₀

The projection of the region of ℝ⁶ that corresponds to w ₁₃ onto Θ ₁ lies on a 4-face g _s ×Θ _C for some s. This 4-face of Θ ₁ is sandwiched by the two 5-faces $\mathcal {F}_{s\pm\frac{1}{2}}\times\varTheta_{\mathrm{C}}$, whose normal vectors determine a plane orthogonal to this 4-face. The proportion of ℝ⁶ that project onto this 4-face is the product of (1) p _⊥(s), the proportion of the aforementioned plane sandwiched between the two normal vectors of the two adjacent 5-faces, and (2) p _∥(s), the proportion of the 4-dimensional space spanned by g _s ×Θ _C that lies inside it.

To calculate p _⊥(s), we note the space between the two normal vectors of $\mathcal {F}_{s\pm\frac{1}{2}}\times\varTheta_{\mathrm{C}}$ can be represented by $\{\psi_{s-\frac{1}{2}}\leq\psi^{*}_{a}\leq\psi_{s+\frac{1}{2}}, \phi^{*}_{a}=\pi/4, r^{*}_{c}=0\}$, so its area inside $\mathcal {B}$ is given by

and p _⊥(s)=V _⊥(s)/V ₂, where V ₂=π is the area of the unit disk.

For p _∥(s), we note g _s ×Θ _C={ψ _a =ψ _s ,ϕ _a =π/4,π/4<ϕ _c <π/2}. The volume of its part inside $\mathcal {B}$ is given by

where $\widetilde{\mathbf {G}}$ is the 4×4 block of G corresponding to its first, fourth, fifth and sixth columns and rows with . Again, the double integral w.r.t. (r _a ,r _c ) was simplified with Lemma 1. The weight w ₁₃ is given by w ₁₃=lim∑ _s V _⊥(s)V _∥(s)/V ₂ V ₄, where $V_{4}=\frac{1}{2}\pi^{2}$ is the volume of a 4-dimensional unit ball. The weight w ₂₀ can be obtained from the duality between $\varTheta_{1}^{0}$ and Θ ₁.

4.4 D.4 The Derivation of w ₀₃

The projection of the region that corresponds to w ₀₃ lies on the 3-face 0×Θ _C, which is adjacent to 5-dimensional surface ∂Θ _A×Θ _C of Θ ₁. The collection of normal vectors of this surface is the elliptic cone $\{\phi^{*}_{a}=\pi/4, r^{*}_{c}=0\}$. Let p _⊥ be the proportion of the 3-dimensional space spanned by this elliptic cone that falls inside this cone and p _∥ be the proportion of the 3-dimensional space spanned by the 3-face 0×Θ _C that falls inside 0×Θ _C. We have

$$ p_\perp=\frac{1}{2}-\frac{1}{\pi}\int_0^{\pi/2} \varsigma\bigl(\bigl(\bar{\mathcal {I}}^*_{\mathrm{A}}\boldsymbol {\varLambda }_a \bigr)^{-1},\psi_a\bigr)\,d\psi_a\quad \mbox{and}\quad p_\parallel=\frac{1}{2}-\frac{1}{\pi}\int _0^{\pi /2}\varsigma(\boldsymbol {\varLambda }_c, \psi_c)\,d\psi_c $$

where function ς is defined in Section 2.2. The weight w ₀₃ is given by w ₀₃=p _⊥ p _∥.

4.5 D.5 The Derivation of w ₂₂ and w ₁₁

Both Θ _A and Θ _C need to be discretized to calculate w ₂₂. The projection of the region of ℝ⁶ that corresponds to w ₂₂ lies on the 4-face $\mathcal {F}^{\mathrm{A}}_{s}\times \mathcal {F}^{\mathrm{C}}_{r}$ for some r and s, where $\mathcal {F}^{\mathrm{A}}_{s}$ is a face of the discretized Θ _A between edges $\boldsymbol {g}^{\mathrm{A}}_{s\pm\frac{1}{2}}$, and $\mathcal {F}^{\mathrm{C}}_{r}$ is similarly defined. This 4-face is adjacent to 5-faces $\mathcal {F}^{\mathrm{A}}_{s}\times\varTheta_{\mathrm{C}}$ and $\varTheta_{\mathrm{A}}\times \mathcal {F}^{\mathrm{C}}_{r}$, whose normal vectors are given by $\{\psi^{*}_{a}=\psi_{s},\phi^{*}_{a}=\pi/4,r^{*}_{c}=0\}$ and $\{\psi^{*}_{c}=\psi_{r},\phi^{*}_{c}=\pi/4,r^{*}_{a}=0\}$, respectively. The proportion of the 2-dimensional subspace between these two normal vectors is given by $p_{\perp}(s,r)=(t^{*}/2\pi)_{\psi^{*}_{c}=\psi_{r}, \psi ^{*}_{a}=\psi_{s}}$.

The 4-face $\mathcal {F}^{\mathrm{A}}_{s}\times \mathcal {F}^{\mathrm{C}}_{r}$ can be expressed as $\{\psi_{s-\frac{1}{2}}<\psi_{a}<\psi_{s+\frac{1}{2}}, \phi_{a}=\pi/4,\psi_{r-\frac{1}{2}}<\psi_{c}<\psi_{r+\frac{1}{2}},\phi_{c}=\pi/4\}$. To calculate its volume inside $\mathcal {B}$, we note the metric tensor $\widetilde{\mathbf {G}}$ is now given by the first, second, fourth and fifth rows and columns of G, and $|\widetilde{\mathbf {G}}|=r_{a}^{2}r_{c}^{2}|\tilde{\mathbf {J}}'\bar{\mathcal {I}}\tilde{\mathbf {J}}|$, where $\tilde{\mathbf {J}}=\mathrm {diag}\{\tilde{\mathbf {J}}_{\mathrm{A}},\tilde{\mathbf {J}}_{\mathrm{C}}\}$ is a 6×4 matrix. We have

where the double integral w.r.t. (r _a ,r _c ) has been solved by Lemma 1. This 4-face takes a proportion of p _∥(s,r)=V _∥(s,r)/V ₄ out of the 4-dimensional space it spans. Combining the above two proportions, we have w ₂₂=lim∑ _s ∑ _r p _⊥(s,r)p _∥(s,r). The weight w ₁₁ can be obtained similarly.

4.6 D.6 The Derivation of w ₁₂

The projection of the region of ℝ⁶ that corresponds to w ₁₂ lies on the 3-face $\boldsymbol {g}^{\mathrm{A}}_{s}\times \mathcal {F}^{\mathrm{C}}_{r}=\{\psi_{r- \frac{1}{2}}<\psi_{c}<\psi_{r+\frac{1}{2}}, \phi_{a}=\phi_{c}=\pi/4, \psi_{a}=\psi_{s}\}$ for some r and s. Its volume inside $\mathcal {B}$ is given by

where $\widetilde{\mathbf {G}}$ is given by the first, fourth and fifth columns and rows of G and $|\widetilde{\mathbf {G}}|=r^{2}_{c}|\tilde{\mathbf {J}}'\bar{\mathcal {I}}\tilde{\mathbf {J}}|$ with $\tilde{\mathbf {J}}=\mathrm {diag}\{{\boldsymbol {r}}_{a},\tilde{\mathbf {J}}_{\mathrm{C}}\}$.

The part of ℝ⁶ whose projection lies on $\boldsymbol {g}^{\mathrm{A}}_{s}\times \mathcal {F}^{\mathrm{C}}_{r}$ is sandwiched between $\boldsymbol {g}^{\mathrm{A}}_{s}\times \mathcal {F}^{\mathrm{C}}_{r}$ and $\{ \psi_{s-\frac{1}{2}}<\psi^{*}_{a}<\psi_{s+\frac{1}{2}}, \phi^{*}_{a}=\phi^{*}_{c}=\pi/4, \psi^{*}_{c}=\psi_{r}\}$. The latter is a part of the 3-dimensional subspace orthogonal to $\boldsymbol {g}^{\mathrm{A}}_{s}\times \mathcal {F}^{\mathrm{C}}_{r}$. Similar to the derivation of V _∥(r,s), we can obtain the volume of this part of the normal space inside $\mathcal {B}$ as

where $\tilde{\mathbf {J}}^{*}=\mathrm {diag}\{\tilde{\mathbf {J}}^{*}_{\mathrm{A}},{\boldsymbol {r}}^{*}_{c}\}$. The weight w ₁₂ is given by $w_{12}=\lim\sum_{s}\sum_{r} V_{\perp}(r,s)V_{\parallel}(r,s)/V_{3}^{2}$, where V ₃=4π/3 is the volume of a 3-dimensional unit ball.