Robust Blind Carrier Frequency Offset Estimation Algorithm for OFDM Systems

Abstract

In this paper, a joint covariance power fitting and phase based blind estimation method for carrier frequency offset (CFO) is proposed for orthogonal frequency division multiplexing (OFDM) systems using constant modulus constellations. Based on the assumption that the channel varies slowly within two adjacent OFDM symbols, the influence of the channel on corresponding covariance values and phase of the two OFDM symbols will be the same. Utilizing this, a robust method is formulated based on covariance power fitting criterion and phase information between two nearby OFDM symbols. The mean square error and bit-error-rate performance of the proposed estimation method is compared with that of the prominent conventional estimation schemes under noisy multipath channels with high delay spreads and Doppler spreads. Based on Monte Carlo simulations, it is shown that the proposed method is robust under different channel conditions and provides more accurate CFO estimates.

Appendix

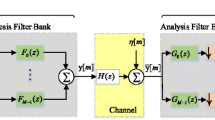
The derivation of the cost function given by (13) is presented in this Appendix. Let the first column of the covariance matrix ${\mathbf{R }}_n\left( \overline{\varepsilon }\right)$ be ${\mathbf r} _m\left( l\right) =\left[ r_m(0),r_m(1),\ldots ,r_m(N-1)\right] ^T$. ${\mathbf{R }}_m\left( \overline{\varepsilon }\right)$is obtained using the matrix ${\mathbf{D }}_m\left( \overline{\varepsilon }\right)$. From (6) and (8), the l-th element of the ${\mathbf{r }}_m\left( l\right)$ vector is obtained as

$$r_m\left( l\right) =\sum ^{N-l-1}_{p=0}{{\hat{d}}_m\left( p+l\right) {{\hat{d}}_m}^*(p)}+\sum ^{N-1}_{p=N-l}{{\hat{d}}_m\left( p+l-N\right) {{\hat{d}}_m}^*\left( p\right) }.$$

(20)

The relationship between $\widehat{\mathbf{d }}_m$ and ${\mathbf{d }}_m$ is obtained from (2), (3) and (6) as

$${{\widehat{\mathbf{d }}}_m}={e^{\frac{-j2\pi \overline{\varepsilon }m\left( N+N_p\right) }{N}}}{{\varvec{\varTheta }}^{*}_{\overline{\varepsilon }}}e^{\frac{j2\pi \varepsilon m\left( N+N_p\right) }{N}}{{\varvec{\varTheta }}_\varepsilon} {{\mathbf{d }}_m} $$

If ${\mathbf{d }}_m=\left[ d_m(0),d_m(1),\ldots ,d_m(N-1)\right] ^T$, the $a^{th}$ element of the vector ${\widehat{\mathbf{d }}}_m$ is given by

$${\hat{d}}_m\left( a\right) =e^{\frac{j2\pi \left( \varepsilon -\overline{\varepsilon }\right) m\left( N+N_p\right) }{N}}e^{\frac{j2\pi \left( \varepsilon -\overline{\varepsilon }\right) a}{N}}d_m\left( a\right) .$$

(21)

Using (21) in (20),

$$r_m\left( l\right) =e^{\frac{j2\pi \left( \varepsilon -\overline{\varepsilon }\right) \left( l\right) }{N}}\sum ^{N-l-1}_{p=0}{d_m\left( p+l\right) {d^*}_m\left( p\right) }+e^{\frac{j2\pi \left( \varepsilon -\overline{\varepsilon }\right) \left( l-N\right) }{N}}\sum ^{N-1}_{p=N-l}{d_n\left( p+l-N\right) {d^*}_m\left( p\right) }.$$

(22)

Let $\sum ^{N-l-1}_{p=0}{d_m\left( p+l\right) {d^*}_m\left( p\right) }$ be ${\lambda }_{m,l}$ and $\sum ^{N-1}_{p=N-l}{d_m\left( p+l-N\right) {d^*}_m\left( p\right) }$ be ${\mu }_{m,l}$. Then

$$r_m\left( l\right) =e^{\frac{j2\pi \left( \varepsilon -\overline{\varepsilon }\right) l}{N}}{(\lambda }_{m,l}+e^{-j2\pi \left( \varepsilon -\overline{\varepsilon }\right) }{\mu }_{m,l}).$$

(23)

Similarly,

$$r_{m+1}\left( l\right) =e^{\frac{j2\pi \left( \varepsilon -\overline{\varepsilon }\right) l}{N}}{(\lambda }_{m+1,l}+e^{-j2\pi \left( \varepsilon -\overline{\varepsilon }\right) }{\mu }_{m+1,l})$$

and

$$\left( r_{m+1}\left( l\right) -r_m\left( l\right) \right) =e^{\frac{j2\pi \left( \varepsilon -\overline{\varepsilon }\right) l}{N}}\left( \left( {\lambda }_{m+1,l}-{\lambda }_{m,l}\right) +e^{-j2\pi \left( \varepsilon -\overline{\varepsilon }\right) }\left( {\mu }_{m+1,l}-{\mu }_{m,l}\right) \right)$$

Let $\left( {\lambda }_{m+1,l}-{\lambda }_{m,l}\right)$=${\lambda }_l$ and $\left( {\mu }_{m+1,l}-{\mu }_{m,l}\right)$=${\mu }_l$. Then ${\left\| r_{m+1}\left( l\right) -r_m\left( l\right) \right\| }^2$ can be minimized to

$${\left\| r_{m+1}\left( l\right) -r_m\left( l\right) \right\| }^2={\left| \lambda _{l} \right| ^2}+ {\left| {\mu }_l \right| ^2}+2{\text {Re}}\left\{ \lambda _{l}\mu ^*_{l}\right\} \cos {2\pi \left( \varepsilon -\overline{\varepsilon }\right) }-2{\text {Im}}\left\{ \lambda ^*_{l}\mu _{l}\right\} \sin {2\pi \left( \varepsilon -\overline{\varepsilon }\right) }.$$

(24)

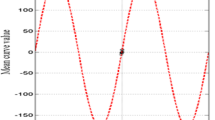
Since the channel characteristics remains invariant between two adjacent OFDM symbols, in the absence of CFO and at high SNR, $r_{m+1}\left( l\right) =r_m\left( l\right)$. Hence, $\left( \lambda _{m+1,l}+\mu _{m+1,l}\right) =\left( \lambda _{m,l}+\mu _{m,l}\right)$. Therefore, $\left( \lambda _{m+1,l}-\lambda _{m,l}\right) =-\left( \mu _{m+1,l}-\mu _{m,l}\right)$. i.e. $\lambda _{l}=-\mu _{l}$. Hence the term ${\text {Im}}\left\{ \lambda ^*_{l}\mu _{l}\right\}$, associated with the sinusoidal term in (24) becomes $-{\text {Im}}\left\{ \left| \lambda _{l}\right| ^2\right\}$ which is zero. Substituting $\lambda _{l}=-\mu _{l}$ in (24), ${\left\| r_{m+1}\left( l\right) -r_m\left( l\right) \right\| }^2=2{\left| \lambda _{l} \right| ^2}-2{\left| \lambda _{l} \right| ^2}\cos {2\pi \left( \varepsilon -\overline{\varepsilon }\right) }$. If, $-2{\left| \lambda _{l} \right| ^2}=A$, ${\left\| r_{m+1}\left( l\right) -r_m\left( l\right) \right\| }^2=A{\cos 2\pi \left( \varepsilon -\overline{\varepsilon }\right) \ }-A$. The constant in the equation is independent of $\left( \varepsilon -\overline{\varepsilon }\right)$ and the cost function of (11) can be approximated as $J\left( \overline{\varepsilon }\right) =A\cos \left( 2\pi \left( \varepsilon -\overline{\varepsilon }\right) \right) -A$.