Skip to main content
SpringerLink
Log in

A Composite Shadowed Fading Model Based on the McKay Distribution and Meijer G Functions

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

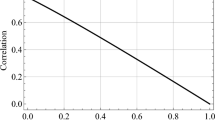
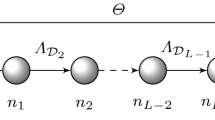
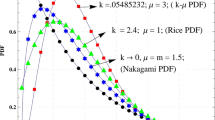
Abstract

The McKay density function has been cited in the study of wireless channels in connection with the analysis of diversity. It is also a forerunner of the \(\upeta \)-\(\upmu \) and \(\upeta \)-\(\uplambda \)-\(\upmu \) distributions in wireless channels. Starting with a physical description of fading in terms of clustering and using the existing results from the original work of Nakagami, the probability density function of the signal-to-noise ratio has been shown to match the three parameter McKay distribution. It is demonstrated that the McKay density also allows for the modeling of wireless channels exhibiting fading levels far worse than what is seen in Nakagami channels, allowing the amount of fading to vary from 0 to \(\infty \). The shadowing in wireless channels is then incorporated in the model using the cascading concept to describe the shadowing. The error rates in such a McKay–Meijer G model are studied using the example of a coherent binary shift keying modem. With the availability of closed form expressions for the density, cumulative distribution function, error rates and outage probabilities, the McKay–Meijer G model offers a very flexible means to study the performance of modems in composite shadowed fading channels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Simon, M. K., & Alouini, M.-S. (2005). Digital communication over fading channels: A unified approach to performance analysis (2nd ed.). Hoboken, NJ: Wiley.

    Google Scholar 

  2. Shankar, P. M. (2012). Fading and shadowing in wireless systems. New York: Springer.

    Book  Google Scholar 

  3. Nakagami, M. (1960). The \(m\)-distribution—A general formula of intensity distribution of rapid fading. In W. C. Hoffman (Ed.), Statistical methods in radio wave propagation. Elmsford, NY: Pergamon.

    Google Scholar 

  4. Yacoub, M. D. (2007). The alpha-mu distribution: A physical fading model for the Stacy distribution. IEEE Transactions on Vehicular Technology, 56, 27–34.

    Article  Google Scholar 

  5. Yacoub, M. D. (2007). The \(\kappa \text{- }\mu \) and \(\eta \text{- }\mu \) distribution. IEEE Antennas and Propagation Magazine, 49, 68–81.

    Article  Google Scholar 

  6. Radaydeh, R. M., & Matalgah, M. M. (2008). Compact formulas for the average error performance of noncoherent m-ary orthogonal signals over generalized Rician, Nakagami-m, and Nakagami-q fading channels with diversity reception. IEEE Transactions on Communications, 56, 32–38.

    Article  Google Scholar 

  7. Papazafeiropoulos, A. K., & Kotsopoulos, S. A. (2011). The \(\alpha \) -\(\lambda \)- \(\mu \) and \(\alpha \) - \(\eta \)- \(\mu \) small-scale general fading distributions: A unified approach. WIRE, 57, 735–751.

    Google Scholar 

  8. McKay, A. T. (1932). A Bessel distribution function. Biometrika, 24, 39–44.

    Article  Google Scholar 

  9. Holm, H. (2002). Adaptive coded modulation performance and channel estimation tools for flat fading channels. Ph. D. Thesis, Department of Telecommunications, Norwegian University of Science and Technology.

  10. Holm, H., & Alouini, M.-S. (2004). Sum and difference of two squared correlated Nakagami variates in connection with the McKay distribution. IEEE Transactions on Communications, 52, 1367–1376.

    Article  Google Scholar 

  11. Shankar, P. M. (2012). A Nakagami-N-gamma model for shadowed fading channels. WIRE, 64, 665–680.

    Google Scholar 

  12. Andersen, J. B. (2002). Statistical distributions in mobile communications using multiple scattering. In Proc. Gen. Assem. Int. Union of Radio Sci. Maastricht, The Netherlands.

  13. Asplund, H., Molisch, A. F., Steinbauer, M., & Mehta, N. B. (2002). Clustering of scatterers in mobile radio channels—Evaluation and modeling in the COST259 directional channel model. In Proc. IEEE ICC, New York (pp. 901–905).

  14. Papoulis, A., & Pillai, S. U. (2002). Probability, random variables and stochastic processes (4th ed.). New York: McGraw-Hill.

    Google Scholar 

  15. Gradshteyn, I. S., & Ryzhik, I. M. (2000). Table of integrals, series, and products (6th ed.). New York: Academic.

    MATH  Google Scholar 

  16. Nadarajah, S., & Kotz, S. (2006). Bivariate gamma distributions, sums and ratios. Bulletin of the Brazilian Mathematical Society New Series, 37, 241–274.

    Article  MATH  MathSciNet  Google Scholar 

  17. Okui, S., Morinaga, N., & Namekawa, T. (1981). Probability distributions of ratio of fading signal envelopes and their generalizations. Electronics and Communications in Japan, 64–B, 1228–1235.

    Google Scholar 

  18. Di Salvo, F. (2008). A characterization of the distribution of a weighted sum of gamma variables through multiple hypergeometric functions. Integral Transforms & Special Function, 19, 563–575.

    Article  MATH  Google Scholar 

  19. Karagiannidis, G. K., Sagias, N. C., & Tsiftsis, T. A. (2006). Closed-form statistics for the sum of squared Nakagami-m variates and its applications. IEEE Transactions on Communications, 54, 1353–1359.

    Article  Google Scholar 

  20. http://functions.wolfram.com/.

  21. Yilmaz, F., & Alouini, M.-S. (2012). A novel unified expression for the capacity and bit error probability of wireless communication systems over generalized fading channels. IEEE Transactions on Communications, 60, 1862–1876.

    Article  Google Scholar 

  22. Wojnar, A. H. (1986). Unknown bounds on performance in Nakagami channels. IEEE Transactions on Communications, 34, 22–24.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical and Computer Engineering, Drexel University, Philadelphia, PA, 19104, USA

    P. M. Shankar

Authors
  1. P. M. Shankar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. M. Shankar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shankar, P.M. A Composite Shadowed Fading Model Based on the McKay Distribution and Meijer G Functions. Wireless Pers Commun 81, 1017–1030 (2015). https://doi.org/10.1007/s11277-014-2168-2

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-014-2168-2

Keywords

Search

Navigation