1 Introduction

An uplink (UL) multi-user multiple-input multiple-output (MU-MIMO) system [1, 2] is an important wireless communication technique for the third generation partnership project (3GPP) long-term evolution (LTE) [3–5], where multiple users (i.e., mobile stations) transmit data to a base station (BS). The MU-MIMO system with the concept of space-division multiple access (SDMA) allows multiple users to BS in the same band simultaneously [2]. In the precoded UL MU-MIMO system, Liu gives contributions in [6] that the singular value decomposition (SVD)-assisted detection structure [7, 8] mainly based on the assumption of perfect channel state information (CSI) estimation was developed to suppress the multiple user interference (MUI) caused by other users, where receiver transmits precoding matrices to users in the transmitted side via an error-free feedback link. However, precoding with the entire CSI feedback in [6] is impractical because the receiver sends all of the CSI to users via a limited feedback channel [9]. Additionally, this conventional detection structure [6] performs terribly due to the involvement of an inaccurate SVD [10] suffered from the effect of uncertain CSI and noise.

Recently, to avoid having to provide the entire CSI, the limited feedback precoding was developed [9], in which the receiver determines the optimal precoder from pre-design codebooks and sends only the index of the selected precoder to users via the limited feedback channel. The feedback related to this index contains fewer bits because codebooks are stored in both the transmitter and receiver for the LTE system [5]. Additionally, robustness against uncertain CSI effect, attracted a lot of attention, was developed in [11–13] to improve the detection performance of the downlink transmission. For MU-MIMO precoding in the limited feedback precoding, the UL, robustness against the effect of the CSI estimation error, will be the major concerned scenario in this paper. On the other hand, the robust design in the limited feedback system has more complicated optimization problem due to the involvement of the non-linear characteristic in SVD [14, 15]. These motivate us to develop a computationally-efficient convex optimization problem to optimize jointly the design of the adaptive and precoder matrices for the robust transceiver design as follows.

For the precoded UL MU-MIMO transmission [6], there is no cooperated among the UL users. By utilizing this no cooperation, we develop the user-wise (or called column-wise) detection that all columns (i.e., MUI) not in selected being detected user, constructed from partial columns of overall MU-MIMO channel, are nulled by column-wise weighting matrix iteratively. With the least-square (LS) estimation technique [16], we can formulate CSI estimation error as a random variable, exploiting property of arbitrary covariance matrix, to resist uncertain CSI for the robust transceiver design. Based on this property, the minimum variance (MV) approach with quadratic form advantageously [17, 18] can realize a computationally-efficient optimization problem [19] to minimize the output power of joint MUI and noise subjecting to constraint while rejects the CSI estimation error. Applying the first-order approximation [19], the non-linear characteristic of SVD can be tractable in proposed MV approach for the expectation computation to acquire a deterministic function of adaptive matrix when the Lagrange multiplier method [19] is considered. Thus, an optimum adaptive matrix [15] can be obtained by selecting an optimum precoder matrix from codebook according to the minimization optimization problem by exploiting this deterministic function. With the optimum adaptive and precoder matrices, an optimum robust column-wise weighting matrix can be obtained to facilitate the user-wise detection in precoded UL MU-MIMO transmission for limited feedback system. Performance analysis shows that the proposed robust weighting matrix is an unbiased design and it also can regularize the diagonal loading (DL) factor technique, and the detection performance of the proposed robust transceiver design can be predicted simplistically by applying our derived signal-to-interference-plus-noise ratio (SINR) formulation. Computer simulations are conducted to confirm the efficacy of the proposed scheme in both perfect and imperfect CSI estimation.

This paper is organized as follows. In Sect. 2, system model and detection scheme is developed to improve UL MU-MIMO precoding in limited feedback system. In Sect. 3, performance analysis is investigated to validate the detection performance of the proposed robust design. In Sect. 4, we conduct computer simulations to confirm the effectiveness of the proposed robust design. In Sect. 5, we present our conclusions. Notation: Matrices and vectors are denoted by upper and lower case boldface letters, respectively. \(\mathbf{I}_{M}\) is an \(M\times M\) identity matrix. For vector \(\mathbf{x},\,x_{i}\) is its \(i\)th entry. Superscript \((\cdot )^{H},\,(\cdot )^{-1}\) and \((\cdot )^{\dagger }\) represent Hermitian transpose. inverse and pesudoinverse operations, respectively. \(E\{\cdot \}\) is an expectation operation, \(tr(\cdot )\) is a trace operation and \(\vert \vert \cdot \vert \vert _{F}\) represents Frobenius norm.

2 System Model and Detection Scheme

In this section, the robust precoded UL MU-MIMO transmission is developed from A) MV-based transceiver design in perfect CSI estimation and B) robust MV-based transceiver design in imperfect CSI estimation as follows.

2.1 MV-Based Transceiver Design in Perfect CSI

In Fig. 1, we here consider a precoded UL MU-MIMO system via an error-free limited feedback link that \(N_{t}\) transmit antennas are equipped for \(Q\) users with 1 \(\le q \le Q\) and \(M_{r}\) receive antennas for \(M_{r}\ge N_{t}\) are serving a BS. Considering the total transmit power of \(Q\) users as \(P=N_{1}+N_{2}+\,{\cdots }\,N_{Q}\), an equivalent UL MU-MIMO system in the limited feedback precoding with user-wise structure under assumption that there is no cooperated among the UL users [6] can be

$$\begin{aligned} \mathbf{y}=\mathbf{H}_q \mathbf{P}_q \mathbf{x}_q +\underbrace{\sum _{i=1,i\ne q}^Q \mathbf{H}_i \mathbf{P}_i \mathbf{x}_i}_{\mathbf{H}_{\mathrm{I},q} \mathbf{P}_{\mathrm{I},q}\mathbf{x}_{\mathrm{I},q}}+\mathbf{v}, \end{aligned}$$
(1)

where \(\mathbf{x}_{q}=[x_{q,1}\quad x_{q,2}\,\ldots \, x_{q,Nq}]^{T}\in C^{Nq\times 1}\) is the transmitted symbol vector at the \(q\)th user, \(\mathbf{y}\in C^{Mr\times 1}\) is the received signal, the MU-MIMO channel matrix can be expressed from the column-wise structure as \(\mathbf{H =}\, [\mathbf{H}_{1}\,\mathbf{H}_{2} {\ldots } \mathbf{H}_{q} {\ldots } \mathbf{H}_{Q}]\in C^{Mr\times Nt}\) with \(N_{t}=N_{1}+N_{2} + \,{\cdots }\, + N_{Q}\) involved the complex Gaussian entries, unitary matrix \(\mathbf{P}_{q}\in C^{Nq\times Nq}\) is an precoder matrix selected from codebook \(\mathcal {F},\,\mathbf{H}_{\mathrm{I},q}\mathbf{P}_{\mathrm{I},q}\mathbf{x}_{\mathrm{I},q}\) denotes MUI given as \(\mathbf{H}_{\mathrm{I},q}\mathbf{P}_{\mathrm{I},q}= [\mathbf{H}_{1}\mathbf{P}_{1}\mathbf{H}_{2}\mathbf{P}_{2}\,{\ldots }\, \mathbf{H}_{q-1}\mathbf{P}_{q-1}\mathbf{H}_{q+1}\mathbf{P}_{q+1}\,{\ldots }\, \mathbf{H}_{Q}\mathbf{P}_{Q}] \in C^{Mr\times (Mr-Nq)}, \mathbf{x}_{\mathrm{I},q} = [\mathbf{x}_1^T \,\ldots \,\mathbf{x}_{q-1}^T \,\mathbf{x}_{q+1}^T \ldots \mathbf{x}_Q^T]^{T}\in C^{(Mr-Nq)\times 1}\) are the transmit signals of users from \(1 \le i \le Q\) at \(i\ne q\) and \(\mathbf{v}\in C^{Mr\times 1}\) has \(i.i.d.\) complex Gaussian entries with noise power \(E\{\mathbf{vv}^{H}\}=\sigma _v^2\mathbf{I}_{Mr}\). Based on this column-wise structure for minimizing the output power of MUI and noise jointly, the constrained minimum variance (MV) approach [17, 18] determines the optimum weight \(\mathbf{W}_{MV,q}\in C^{Mr\times Nq}\) given as

$$\begin{aligned} \mathbf{W}_{\mathrm{MV},q}, \mathbf{P}_{\mathrm{MV},q} \!=\!\mathop {\arg \min }\limits _{\mathbf{w}_q,\mathbf{P}_q \in {\mathcal {F}}} \quad tr\left( {\mathbf{W}_q^H \mathbf{R}_{\mathrm{I},q}\mathbf{W}_q} \right) \quad s.t.\, \left| \left| \mathbf{W}_q^H \mathbf{y} \right| \right| _F^2 \approx \left| \left| \left( \mathbf{H}_q \mathbf{P}_q\right) ^{H}\mathbf{H}_q \mathbf{P}_q \mathbf{x}\right| \right| _F^2,\nonumber \\ \end{aligned}$$
(2)

where involves the distortion response due to inequality in constraint and \(\mathbf{R}_{\mathrm{I}, q} =\mathbf{H}_{\mathrm{I},q} \mathbf{P}_{\mathrm{I},q} (\mathbf{H}_{\mathrm{I}, q} \mathbf{P}_{\mathrm{I},q})^{H}+\sigma _v^2 \mathbf{I}_{Mr} \in C^{Mr\times Mr}\) is the output power of MUI and noise. By applying the adaptive technique in [14, 15] as \(\left( \mathbf{H}_{q}\mathbf{P}_{q}-\mathbf{B}_{q}\mathbf{A}_{q}\right) ^{H}\mathbf{y}\approx \left( \mathbf{H}_{q}\mathbf{P}_{q}\right) ^{H}\mathbf{H}_{q}\mathbf{P}_{q}\mathbf{x}_{q}\), the optimization problem of (2) is converted into an unconstrained optimization problem and hence an optimum adaptive matrix and an optimum precoder can be obtained by applying MV approach as

$$\begin{aligned} \mathbf{A}_{\mathrm{MV},q},\mathbf{P}_{\mathrm{MV},q} =\mathop {\arg \min }\limits _{\mathbf{A}_q, \mathbf{P}_q \in {\mathcal {F}}} \quad tr\left\{ {\left( {\mathbf{H}_q \mathbf{P}_q -\mathbf{B}_q \mathbf{A}_q } \right) ^{H}\mathbf{R}_{\mathrm{I},q}\left( {\mathbf{H}_q \mathbf{P}_q -\mathbf{B}_q\mathbf{A}_q}\right) }\right\} , \end{aligned}$$
(3)

where \(\mathbf{A}_{q}\) is an adaptive matrix, \(\mathbf{P}_{q}\in C^{Nq\times Nq}\) is a precoder matrix selected from codebook \({\mathcal {F}}\), the blocking matrix \(\mathbf{B}_{q}\in C^{Mr\times (Mr-Nq)}\) can be obtained from SVD \(\mathbf{H}_{q}\mathbf{P}_{q} = \mathbf{U}_{q}{\varvec{\Lambda }}_{q}\mathbf{V}_{q}\) as \(\mathbf{U}_{q} = [\mathbf{U}_{D,q}\mathbf{B}_{q}] \in C^{Mr\times Mr}\) with \(\mathbf{U}_{D,q}\in C^{Mr\times Nq}\), and then the cost function according to (3) can be given as

$$\begin{aligned} h\left( {\mathbf{A}_q, \mathbf{P}_q } \right) =\left( {\mathbf{H}_q \mathbf{P}_q -\mathbf{B}_q \mathbf{A}_q } \right) ^{H}\mathbf{R}_{\mathrm{I},q} \left( {\mathbf{H}_q \mathbf{P}_q -\mathbf{B}_q \mathbf{A}_q } \right) . \end{aligned}$$
(4)

With \(\partial h(\mathbf{A}_{q},\mathbf{P}_{q})/\partial \mathbf{A}_{q}) = \mathbf{0}\) on (4), the optimization problem of (3) with the Lagrange multiplier method [19] can be expressed as

$$\begin{aligned} \mathbf{A}_q =\left( {\mathbf{B}_q^H \mathbf{R}_{\mathrm{I,} q} \mathbf{B}_q } \right) ^{-1}\mathbf{B}_q^H \mathbf{R}_{\mathrm{I}, q} \mathbf{H}_q \mathbf{P}_q \in C^{(M_r -N_q )\times N_q }.\quad \end{aligned}$$
(5)

By exploiting (5), various adaptive matrices can be computed via various precoder matrices selected from codebook iteratively, and thus an optimal adaptive matrix \(\mathbf{A}_{\mathrm{MV},q}\) and an optimal precoder matrix \(\mathbf{P}_{\mathrm{MV},q}\) can be obtained according to minimize the trace value of cost function of (4) as

$$\begin{aligned} \mathbf{A}_{\mathrm{MV},q}, \mathbf{P}_{\mathrm{MV},q} =\mathop {\arg \min }\limits _{\mathbf{A}_q,\mathbf{P}_q\in {\mathcal {F}}} tr\left( {h\left( {\mathbf{A}_q,\mathbf{P}_q}\right) }\right) , \end{aligned}$$
(6)

where the minimum optimization problem is equivalent to maximize SINR and thus an optimum weighting matrix with the MV approach can be expressed as

$$\begin{aligned} \mathbf{W}_{\mathrm{MV},q} \!=\!\mathbf{H}_q \mathbf{P}_{\mathrm{MV},q} -\mathbf{B}_{\mathrm{MV},q} \mathbf{A}_{\mathrm{MV},q},\quad \end{aligned}$$
(7)

where the MV-based blocking matrix \(\mathbf{B}_{\mathrm{MV},q}\) is obtained from \(\mathbf{H}_{q}\mathbf{P}_{\mathrm{MV},q}\) and the MV-based adaptive matrix is given as

$$\begin{aligned} \mathbf{A}_{\mathrm{MV},q} =\left( {\mathbf{B}_{\mathrm{MV},q}^H \mathbf{R}_{\mathrm{MVI,} q} \mathbf{B}_{\mathrm{MV},q} } \right) ^{-1}\mathbf{B}_{\mathrm{MV},q}^H \mathbf{R}_{\mathrm{MVI,} q} \mathbf{H}_q \mathbf{P}_{\mathrm{MV},q} \in C^{(M_r-N_q)\times N_q }, \end{aligned}$$
(8)

where \(\mathbf{R}_{\mathrm{MVI}, q} =\mathbf{H}_{\mathrm{I}, q} \mathbf{P}_{\mathrm{MVI},q} (\mathbf{H}_{\mathrm{I}, q} \mathbf{P}_{\mathrm{MVI},q})^{H}+\sigma _v^2\mathbf{I}_{Mr} \in C^{Mr\times Mr},\,\mathbf{H}_{I,q}\mathbf{P}_{\mathrm{MVI},q}= [\mathbf{H}_{1}\mathbf{P}_{\mathrm{MV},1}\mathbf{H}_{2}\mathbf{P}_{\mathrm{MV},2}{\ldots }\mathbf{H}_{q-1}\mathbf{P}_{\mathrm{MV},q-1}\mathbf{H}_{q+1}\mathbf{P}_{\mathrm{MV},q+1}{\ldots }\mathbf{H}_{Q}\mathbf{P}_{\mathrm{MV},Q}] \in C^{Mr\times (Mr-Nq)}\) and \(\mathbf{P}_{\mathrm{MV},q}\) is a precoder matrix selected from codebook according to (6). Noted that the MV approach in (3) under assumption that the exact CSI is available [6]; when the exact CSI is unavailable in practical implementation, the detection performance with (7) will be degraded severely resulted from the singular problem in the optimal adaptive matrix of (8) since channel parameter mismatch occurs. This degrades because the suppression of CSI estimation error effect is not considered in designing the weighting matrix. Therefore, to achieve more degrees of freedom with the interference alignment technique, a computationally-efficient convex optimization problem for optimizing adaptive matrix and precoder simultaneously to resist uncertain CSI is thus developed in follows.

Fig. 1
figure 1

A precoded UL MU-MIMO transmission for limited feedback system in which the receiver transmits the index of precoder of codebook to users via an error-free limited feedback link

Full size image

2.2 Robust MV-Based Transceiver Design in Imperfect CSI

In this section, the design problem of the robust MV-based transceiver to suppress the effect of the CSI estimation error, MUI and noise jointly in UL MU-MIMO system for limited feedback precoding is investigated. By exploiting the LS estimation on the formulation of uncertain CSI [18], we can obtain the deterministic function associated with optimizing jointly design of precoder and adaptive matrices by applying the first-order approximation on the expression of the estimated block matrix to achieve an optimum weighting to facilitate user-wise detection. In the imperfect CSI estimation, the estimated UL MU-MIMO channel with column-wise structure can be expressed as

$$\begin{aligned} {\hat{\mathbf{H}}}&= \left[ {\mathbf{H}_1 \mathbf{H}_2 \cdots \mathbf{H}_Q } \right] +\left[ {\Delta \mathbf{H}_1 \Delta \mathbf{H}_2 \cdots \Delta \mathbf{H}_Q } \right] =\left[ {{\hat{\mathbf{H}}}_1 {\hat{\mathbf{H}}}_2 \cdots {\hat{\mathbf{H}}}_Q } \right] =\mathbf{H}+\Delta \mathbf{H}, \end{aligned}$$
(9)

where the estimation error \(\Delta \mathbf{H}\in C^{Mr\times Nt}\) has \(i.i.d.\) Gaussian entries since the entries of the noise v are Gaussian entries depicted in (1) and it involves \(E\{\Delta \mathbf{H}_{q}(\Delta \mathbf{H}_{q})^{H}\} = \frac{N_q \sigma _e^2}{P}\mathbf{I}_{N_q\times N_q}\) and \(E(\Delta \mathbf{H}) = \mathbf{0}\). When the CSI estimation is imperfect, the optimization problem with column-wise structure via (3) for minimizing the output power of MUI and noise to find an optimum adaptive matrix \(\mathbf{A}_{\mathrm{RMV},q}\in C^{(Mr-Nq)\times Nq}\) and an optimum precoder \(\mathbf{P}_{\mathrm{RMV},q}\) is formulated as

$$\begin{aligned} \mathbf{A}_{\mathrm{RMV},q},\mathbf{P}_{\mathrm{RMV},q}&= \mathop {\arg \min }\limits _{\mathbf{A}_q,\mathbf{P}_q \in {\mathcal {F}}} \,tr\left\{ {E\left[ {\left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q } \right) ^{H}\mathbf{R}_{\mathrm{I},q} \left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q } \right) } \right] } \right\} \nonumber \\&s.t.\quad E\left\| {\left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q } \right) ^{H}\Delta \mathbf{H}_q \mathbf{P}_q } \right\| _F^2 \approx 0, \end{aligned}$$
(10)

where the estimated blocking matrix \({\hat{\mathbf{B}}}_q =\mathbf{B}_q +\Delta \mathbf{B}_q\in C^{Mr\times (Mr-Nq)}\) with \(\mathbf{B}_q^H \mathbf{H}_q \mathbf{P}_q =\mathbf{0}\) and \({\hat{\mathbf{B}}}_q^H \mathbf{H}_q \mathbf{P}_q \ne \mathbf{0}\), and it is obtained from SVD \({\hat{\mathbf{H}}}_q \mathbf{P}_q ={\hat{\mathbf{U}}}_q {\hat{\varvec{\Lambda }}}_q {\hat{\mathbf{V}}}_q\) as \({\hat{\mathbf{U}}}=[{\hat{\mathbf{U}}}_{D,q}\quad {\hat{\mathbf{B}}}_q]\in C^{Mr\times Mr}\) with \({\hat{\mathbf{U}}}_{D,q} \in C^{Mr\times Nq}\) and constraint particularly involves the suppression of effect of CSI estimation error. For simplicity, the constrain of optimization problem in (10) to find an optimum adaptive matrix via the expectation method is expressed as

$$\begin{aligned} tr\left( {\frac{N_q \sigma _e^2 }{P}\left( {\mathbf{H}_q \mathbf{P}_q } \right) ^{H}\mathbf{H}_q \mathbf{P}_q +\mathbf{A}_q^H \mathbf{A}_q )} \right) =E\left\| {\left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q } \right) ^{H}\Delta \mathbf{H}_q \mathbf{P}_q } \right\| _F^2, \end{aligned}$$
(11)

where expressed terms in (11) is a quadratic function and thus (10) with this expressed constrain can be relaxed as

$$\begin{aligned} \mathbf{A}_{\mathrm{RMV},q},\mathbf{P}_{\mathrm{RMV},q}&= \mathop {\arg \min }\limits _{\mathbf{A}_q,\mathbf{P}_q \in {\mathcal {F}}} \,tr\left\{ {E\left[ {\left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q } \right) ^{H}\mathbf{R}_{\mathrm{I},q}\left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q } \right) } \right] } \right\} \nonumber \\&s.t.\quad tr\left( {\frac{N_q \sigma _e^2 }{P}\left( {\mathbf{H}_q \mathbf{P}_q } \right) ^{H}\mathbf{H}_q \mathbf{P}_q +\mathbf{A}_q^H \mathbf{A}_q )} \right) =0, \end{aligned}$$
(12)

Further, we will show that the proposed optimization problem in (12) is convex as following Theorem 1.

Theorem 1

If  \(\mathbf{P}_{q}\) and \(\mathbf{A}_{q}\) are a precoder matrix and an adaptive matrix, respectively in (12), then the optimization problem in (12) is convex.

Proof

In (12), the object function is a quadratic function since \(\mathbf{R}_{\mathrm{I},q}\) has positive entries and \({\hat{\mathbf{w}}}_{i,q}^H \mathbf{R}_{\mathrm{I},q} {\hat{\mathbf{w}}}_{i,q} \ge 0\) with \(1 \le i \le N_{q}\) where \({\hat{\mathbf{w}}}_{i,q}\) is the \(i\)th column of \({\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q\mathbf{A}_q\) at the \(q\)th user depicted in [19]. Thus, the optimization problem by exploiting the quadratic form on constrain in (12) is convex.

By applying the Lagrange multiplier method [19], the cost function according to (12) is given as

$$\begin{aligned} f\left( {\mathbf{A}_q,\mathbf{P}_q}\right)&= E\left[ {\left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q} \right) ^{H}\mathbf{R}_{\mathrm{I},q} \left( {{\hat{\mathbf{H}}}_q \mathbf{P}_q -{\hat{\mathbf{B}}}_q \mathbf{A}_q } \right) } \right] \nonumber \\&\quad +\,\alpha \frac{N_q \sigma _e^2}{P}\left( {\left( {\mathbf{H}_q \mathbf{P}_q}\right) ^{H}\mathbf{H}_q \mathbf{P}_q+\mathbf{A}_q^H \mathbf{A}_q } \right) , \end{aligned}$$
(13)

where \(\alpha \) is a Lagrange multiplier. With derivative on (13) (i.e., \(\partial f(\mathbf{A}_{q},\mathbf{P}_{q})/\partial \mathbf{A}_{q})\), we have

$$\begin{aligned} f^{\prime }\left( {\mathbf{A}_q,\mathbf{P}_q}\right) =\left( {E\left( {{\hat{\mathbf{B}}}_q^H \mathbf{R}_{\mathrm{I},q} {\hat{\mathbf{B}}}_q} \right) \!+\!\alpha \frac{N_q \sigma _e^2}{P}\mathbf{I}_{M_r -N_q}} \right) \mathbf{A}_q\!-\!E\left( {{\hat{\mathbf{B}}}_q^H \mathbf{R}_{\mathrm{I},q} {\hat{\mathbf{H}}}_q \mathbf{P}_q}\right) \!=\!0.\quad \end{aligned}$$
(14)

Without complicated search problem by applying the Lagrange scheme [18], (14) shows that the optimal weighting matrix via a computationally-efficient convex optimization problem of (12) can be obtained simplistically. However, the estimation error term \(\Delta \mathbf{B}_{q}\) is not easy to evaluate the expectation due to the involvement of the non-linear characteristic in SVD. To solve this non-linear characteristic, the estimation error term of blocking matrix (i.e., \(\Delta \mathbf{B}_{q}\)) by following the first-order approximation [19] for finding an optimum adaptive matrix can be denoted as Lemma 1.

Lemma 1

Let \(\mathbf{P}_{q}\in {\mathcal {F}}\) be a precoder matrix, the estimation error term of blocking matrix can be approximated as

$$\begin{aligned} \Delta \mathbf{B}_q^H \approx -\mathbf{B}_q^H \Delta \mathbf{H}_q \mathbf{H}_q^{\dagger }, \end{aligned}$$
(15)

where \(\Delta \mathbf{B}_{q}\) is an \(M_{r}\times (M_{r}-N_{q})\) complex matrix and \(\mathbf{H}_q^{\dagger } \) denotes the pseudoinverse of the matrix \(\mathbf{H}_{q}\).

Proof

With \({\hat{\mathbf{B}}}_q^H {\hat{\mathbf{H}}}_q \mathbf{P}_q =\mathbf{0}\) and \(\mathbf{B}_q^H \mathbf{H}_q \mathbf{P}_q =\mathbf{0}\), we have

$$\begin{aligned} \mathbf{B}_q^H \mathbf{H}_q \mathbf{P}_q +\mathbf{B}_q^H \Delta \mathbf{H}_q \mathbf{P}_q +\Delta \mathbf{B}_q^H \mathbf{H}_q \mathbf{P}_q +\Delta \mathbf{B}_q^H \Delta \mathbf{H}_q \mathbf{P}_q =\mathbf{0}, \end{aligned}$$
(16)

where \({\hat{\mathbf{B}}}_q\) and \(\mathbf{B}_{q}\) are computed from \({\hat{\mathbf{H}}}_q \mathbf{P}_q\) and \(\mathbf{H}_{q}\mathbf{P}_{q}\), respectively. By applying the first-order approximation in (16), \(\Delta \mathbf{B}_{q}\) can be achieved to (15) since the second-moment term \(\Delta \mathbf{B}_q^H\Delta \mathbf{H}_q\) can be neglected \((\approx \mathbf{0})\).

To compute \(\mathbf{A}_{q}\) with Lemma 1, the expected values with \(E(\Delta \mathbf{B}_{q})=E(\Delta \mathbf{H}_{q})=\mathbf{0}\) via the LS technique on channel estimation in (14) can be expressed as

$$\begin{aligned} E\left\{ {{\hat{\mathbf{B}}}_q^H \mathbf{R}_{\mathrm{I}, q}{\hat{\mathbf{H}}}_q \mathbf{P}_q}\right\} =\mathbf{B}_q^H\mathbf{R}_{\mathrm{I},q}\mathbf{H}_q\mathbf{P}_q, \end{aligned}$$
(17)

and

$$\begin{aligned} E\left\{ {{\hat{\mathbf{B}}}_q^H \mathbf{R}_{\mathrm{I}, q} {\hat{\mathbf{B}}}_q} \right\}&= \mathbf{B}_q^H \mathbf{R}_{\mathrm{I}, q} \mathbf{B}_q +E\left( {\Delta \mathbf{B}_q^H \mathbf{R}_{\mathrm{I}, q} \Delta \mathbf{B}_q}\right) \nonumber \\&= \mathbf{B}_q^H \mathbf{R}_{\mathrm{I}, q} \mathbf{B}_q +\frac{N_q \sigma _e^2}{P}tr\left( {\mathbf{H}_q^{\dagger } \mathbf{R}_{\mathrm{I},q} \left( {\mathbf{H}_q^{\dagger }}\right) ^{H}} \right) \mathbf{I}_{Mr-Nq}, \end{aligned}$$
(18)

Based on (17) and (18), a deterministic function of adaptive matrix \(\mathbf{A}_{q}\) in (12) against uncertain CSI can be expressed as

$$\begin{aligned} \mathbf{A}_q&= \left( \alpha \frac{N_q \sigma _e^2 }{P}\mathbf{I}_{M_r -N_q } +\mathbf{B}_q^H \mathbf{R}_{\mathrm{I,} q} \mathbf{B}_q \right. \nonumber \\&\quad \left. +\,\frac{N_q \sigma _e^2 }{P}tr\left( {\mathbf{H}_q^{\dagger } \mathbf{R}_{\mathrm{I},q} \left( {\mathbf{H}_q^{\dagger } } \right) ^{H}} \right) \mathbf{I}_{M_r -N_q } \right) ^{-1}\mathbf{B}_q^H \mathbf{R}_{\mathrm{I,} q} \mathbf{H}_q \mathbf{P}_q, \end{aligned}$$
(19)

where the adaptive matrix \(\mathbf{A}_{q}\) is on average optimal choice to suppress the effect of MUI and noise under assumption that CSI estimation error is white, and it involves two additional terms compared with the perfect channel estimation case in (5) to suppress the signal leakage effect resulted from \({\hat{\mathbf{B}}}_q^H \mathbf{H}_q \mathbf{P}_q \ne \mathbf{0}\). To achieve an optimum adaptive matrix, we show that Lagrange multiplier \(\alpha \) in (19) can be established as follows.

Property 1

Suppose that design of optimization problem in (12) is associated with the rejection of interference to obtain an optimum adaptive matrix \(\mathbf{A}_{q}\), we say that Lagrange multiplier with \(\alpha = 1\) can be optimally used in computing \(\mathbf{A}_{q}\) of (19).

Proof

See “Appendix A”.

By exploiting this deterministic function in (19), various adaptive matrices can be computed via various precoder matrices selected from codebook iteratively, and thus an optimal adaptive matrix \(\mathbf{A}_{\mathrm{RMV},q}\) and an optimal precoder matrix \(\mathbf{P}_{\mathrm{RMV},q}\) can be obtained according to minimize the trace value of cost function of (13) as

$$\begin{aligned} \mathbf{A}_{\mathrm{RMV},q},\mathbf{P}_{\mathrm{RMV},q}=\mathop {\arg \min }\limits _{\mathbf{A}_q,\mathbf{P}_q \in {\mathcal {F}}}\,tr\left( {f\left( {\mathbf{A}_q,\mathbf{P}_q}\right) } \right) , \end{aligned}$$
(20)

where the minimum optimization problem is equivalent to maximize SINR and thus the proposed robust MV-based (RMV) weighting matrix at the \(q\)th user under assumption that exact CSI is unavailable as

$$\begin{aligned} {\hat{\mathbf{W}}}_{\mathrm{RMV},q} ={\hat{\mathbf{H}}}_q \mathbf{P}_{\mathrm{RMV},q} -{\hat{\mathbf{B}}}_{\mathrm{RMV},q} {\hat{\mathbf{A}}}_{\mathrm{RMV},q}, \end{aligned}$$
(21)

where the RMV-based adaptive matrix is

$$\begin{aligned} {\hat{\mathbf{A}}}_{\mathrm{RMV},q} \!&= \!\left( {{\hat{\mathbf{B}}}_{\mathrm{RMV}, q}^H {\hat{\mathbf{R}}}_{\mathrm{RMVI,} q} {\hat{\mathbf{B}}}_{\mathrm{RMV}, q} \!+\!\frac{N_q \sigma _e^2 }{P}\left( {1\!+\!tr\left( {{\hat{\mathbf{H}}}_q^{\dagger } {\hat{\mathbf{R}}}_{\mathrm{RMVI},q} \left( {{\hat{\mathbf{H}}}_q^{\dagger } } \right) ^{H}} \right) \mathbf{I}_{M_r -N_q } } \right) } \right) ^{-1}\nonumber \\&\quad {\hat{\mathbf{B}}}_{\mathrm{RMV}, q}^H {\hat{\mathbf{R}}}_{\mathrm{RMVI,} q} {\hat{\mathbf{H}}}_q \mathbf{P}_{\mathrm{RMV},q}, \end{aligned}$$
(22)

where the RMV-based blocking matrix \({\hat{\mathbf{B}}}_{\mathrm{RMV},q}\) is obtained from \({\hat{\mathbf{H}}}_q \mathbf{P}_{\mathrm{RMV},q}\) and \({\hat{\mathbf{R}}}_{\mathrm{RMVI}, q} ={\hat{\mathbf{H}}}_{\mathrm{I}, q} \mathbf{P}_{\mathrm{RMVI},q} ({\hat{\mathbf{H}}}_{\mathrm{I}, q} \mathbf{P}_{\mathrm{RMVI},q} )^{H}+\sigma _v^2 \mathbf{I}_{Mr} \in C^{Mr\times Mr}\) and \({\hat{\mathbf{H}}}_{\mathrm{I}, q} \mathbf{P}_{\mathrm{RMVI},q}\) = \([{\hat{\mathbf{H}}}_1 \mathbf{P}_{\mathrm{RMVI},1} {\hat{\mathbf{H}}}_2 \mathbf{P}_{\mathrm{RMVI},2}\) \({\ldots } {\hat{\mathbf{H}}}_{q-1} \mathbf{P}_{\mathrm{RMVI},q-1}{\hat{\mathbf{H}}}_{q+1} \mathbf{P}_{\mathrm{RMVI},q+1}\quad {\ldots }{\hat{\mathbf{H}}}_Q \mathbf{P}_{\mathrm{RMVI},Q}]\in C^{Mr\times (Mr-Nq)}\). In (21), we note that the design of the proposed \({\hat{\mathbf{W}}}_{\mathrm{RMV},q} \) is simplified since the covariance matrix of the CSI estimation error can be simply obtained via the independent characteristic between signal and noise compared with obtaining actual channel error. To improve the user-wise detection performance, we apply (21) to suppress the effect of noise, MUI and CSI estimation error to derive the RMV-based transceiver in the UL MU-MIMO precoding system as

$$\begin{aligned} {\hat{\mathbf{W}}}_{\mathrm{RMV},q}^H \mathbf{y}={\hat{\mathbf{W}}}_{\mathrm{RMV},q}^H \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \mathbf{x}_q +\underbrace{{\hat{\mathbf{W}}}_{\mathrm{RMV},q}^H \left( {\mathbf{H}_{\mathrm{I,}q} \mathbf{P}_{\mathrm{RMVI},q} \mathbf{x}_{\mathrm{I,}q} +\mathbf{v}} \right) }_{\approx \hbox {0}}. \end{aligned}$$
(23)

With (23), the transmit signal at the \(q\)th user can be estimated as

$$\begin{aligned} {\hat{\mathbf{x}}}_q =slice\left( {\left( {{\hat{\mathbf{W}}}_{\mathrm{RMV},q}^H {\hat{\mathbf{H}}}_q \mathbf{P}_{\mathrm{RMV},q} } \right) ^{{\dagger }}{\hat{\mathbf{W}}}_{\mathrm{RMV},q}^H \mathbf{y}} \right) . \end{aligned}$$
(24)

By exploiting the characteristic of CSI estimation error via the LS technique in optimization problem of (12), the proposed RMV-based weighting matrix can tackle the effects of MUI, noise and parameter mismatch resulted from the CSI estimation error. Hence, an accurate pesudoinverse process can be obtained to improve the user-wise detection performance in (24). Based on (21) and (24), we then summarize the algorithm of the robust MV-based transceiver under the involvement of codebook in UL MU-MIMO precoding for limited feedback system as following Table 1.

Table 1 The algorithm of RMV-based transceiver
Full size table

3 Performance Analysis

In this section, the proposed robust transceiver design to optimize the precoded UL MU-MIMO transmission is validated by applying the analyses of A) Mean characteristic B) Regularization of the DL factor C) SINR formulation and D) Computational complexity.

3.1 Mean Characteristic

In this subsection, we show that the proposed robust weighting matrix \({\hat{\mathbf{W}}}_{\mathrm{RMV},q}\) is an unbiased design via the mean characteristic by applying the first-order approximation. However, this analysis suffers from complicated problem in the expectation operation due to the involvement of a lot of estimated terms. To simply this analysis with the LS technique on the CSI estimation, the mean of \({\hat{\mathbf{W}}}_{\mathrm{RMV},q}\) will be analyzed under the consideration of \(\sigma _e^2 \rightarrow 0\) and \(E({\hat{\mathbf{H}}}) = \mathbf{H}\) as follows:

$$\begin{aligned} E\left( {{\hat{\mathbf{W}}}_{\mathrm{RMV},q} |{\hat{\mathbf{H}}}} \right)&= \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} -E\left( {{\hat{\mathbf{B}}}_{\mathrm{RMV,}q} {\hat{\mathbf{A}}}_{\mathrm{RMV},q} } \right) \approx \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q}\nonumber \\&\quad -\,\mathbf{B}_q \left( {\mathbf{B}_{\mathrm{RMV},q}^H \mathbf{R}_{\mathrm{RMVI,} q} \mathbf{B}_{\mathrm{RMV},q} } \right) ^{-1}\mathbf{B}_{\mathrm{RMV},q}^H \mathbf{R}_{\mathrm{RMVI,} q} \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q},\nonumber \\ \end{aligned}$$
(25)

where (25) is expressed in “Appendix B” and it indicates that \({\hat{\mathbf{W}}}_{\mathrm{RMV},q}\) is an unbiased design [20] due to

$$\begin{aligned} E\left[ {\left( {{\hat{\mathbf{W}}}_{\mathrm{RMV},q} -\mathbf{W}_{\mathrm{MV},q} } \right) |\mathbf{H}} \right] =0, \end{aligned}$$
(26)

where (26) holds due to the consideration of \(\mathbf{P}_{\mathrm{RMV},q }= \mathbf{P}_{\mathrm{MV},q}\) under giving perfect CSI.

3.2 Regularization of the DL Factor

In this subsection, the regularization of the DL factor in [17, 18] is emphasized to perfectly mitigate the effect of MUI, noise and CSI estimation error via the proposed robust weighting matrix in (22). Considering the LS technique [16], the key technique of the conventional DL scheme with additional \(\gamma \) [17, 18] in the quadratic term of (5) is

$$\begin{aligned} {\hat{\mathbf{A}}}_{DL} \!=\!\left( {\gamma \mathbf{I}_{Mr-Nq} \!+\!{\hat{\mathbf{B}}}_{\mathrm{RMV},q}^H {\hat{\mathbf{R}}}_{\mathrm{RMVI}, q} {\hat{\mathbf{B}}}_{\mathrm{RMV},q}}\right) ^{-1}{\hat{\mathbf{B}}}_{\mathrm{RMV},q}^H {\hat{\mathbf{R}}}_{\mathrm{RMVI},q}{\hat{\mathbf{H}}}_q \mathbf{P}_{\mathrm{RMV},q},\quad \end{aligned}$$
(27)

where \(\gamma \) is a DL factor and it is associated with the MIMO detection performance depicted in [17]. However, the computation of \(\gamma \) in (27) is a difficult problem since it has no any feasible set corresponded to the characteristic of channel estimation error. To solve this problem in (27), the optimization of \(\gamma \) can be regularized as

$$\begin{aligned} \gamma =\frac{N_q \sigma _e^2}{P}\left( {1+tr\left( {{\hat{\mathbf{H}}}_q^{\dagger }{\hat{\mathbf{R}}}_{\mathrm{RMVI},q} \left( {{\hat{\mathbf{H}}}_q^{\dagger }}\right) ^{H}} \right) } \right) , \end{aligned}$$
(28)

where \(\alpha = 1\) in (22) gives a feasible solution for the formulation of \(\gamma \) to suppress the signal leakage effect, and it also provides the ability of the matrix inversion to resist the singular problem resulted from \({\hat{\mathbf{B}}}_{\mathrm{RMV},q}^H {\hat{\mathbf{R}}}_{\mathrm{RMVI},q}{\hat{\mathbf{B}}}_{\mathrm{RMV},q}\).

3.3 SINR Formulation

In this section, the derived SINR formulation with the expectation operation is investigated to address the ability of the interference mitigation in the proposed robust design at Table 1. When variance of CSI estimation error is given, this derived SINR formulation, invoking the characteristic of CSI estimation error of LS technique, based on the matrix inverse lemma of [21] and the expression of \(\Delta \mathbf{B}_{q}\) can be obtained approximately.

By referring [14], we have

$$\begin{aligned} \Delta \mathbf{W}_{\mathrm{RMV,}q}&= {\hat{\mathbf{W}}}_{\mathrm{RMV,}q} -\mathbf{W}_{\mathrm{RMV,}q} \approx \Delta \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} -\Delta \mathbf{B}_q \mathbf{X}_{1,q} \mathbf{B}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI},q} \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \nonumber \\&\quad +\,\mathbf{B}_{\mathrm{RMV,}q} \mathbf{X}_{1,q} \Delta \mathbf{B}_q^H \mathbf{R}_{\mathrm{RMVI},q} \mathbf{B}_{\mathrm{RMV,}q} \mathbf{X}_{1,q} \mathbf{B}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI},q} \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \nonumber \\&\quad +\,\mathbf{B}_{\mathrm{RMV,}q} \mathbf{X}_{1,q} \mathbf{B}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI},q} \Delta \mathbf{B}_q \mathbf{X}_{1,q} \mathbf{B}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI},q} \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \nonumber \\&\quad +\,\mathbf{B}_{\mathrm{RMV,}q} \mathbf{X}_{1,q} \Delta \mathbf{B}_q^H \mathbf{R}_{\mathrm{RMVI},q} \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q}\nonumber \\&\quad +\,\mathbf{B}_{\mathrm{RMV,}q} \mathbf{X}_{1,q} \mathbf{B}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI},q} \Delta \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q}, \end{aligned}$$
(29)

where \(\mathbf{X}_{1,q}\) is defined in “Appendix C”, \(\mathbf{W}_{\mathrm{RMV},q}\) is an exact solution of \({\hat{\mathbf{W}}}_{\mathrm{RMV},q}\) and the deviation is \(\Delta \mathbf{W}_{\mathrm{RMV},q}={\hat{\mathbf{W}}}_{\mathrm{RMV},q}-\mathbf{W}_{\mathrm{RMV},q}\) referred in (43). Based on (29), the robust weight matrix multiplied by received signal can be expressed as

$$\begin{aligned} {\hat{\mathbf{W}}}_{\mathrm{RMV,}q}^H \mathbf{y}&= {\hat{\mathbf{W}}}_{\mathrm{RMV,}q}^H \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \mathbf{x}_q +{\hat{\mathbf{W}}}_{\mathrm{RMV,}q}^H \left( {\mathbf{H}_\mathrm{I} \mathbf{P}_{\mathrm{RMVI},q} \mathbf{x}_\mathrm{I} +\mathbf{v}} \right) \nonumber \\&= \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \mathbf{x}_q\nonumber \\&\quad +\underbrace{\Delta \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \mathbf{x}_q +{\hat{\mathbf{W}}}_{\mathrm{RMV,}q}^H \left( {\mathbf{H}_\mathrm{I} \mathbf{P}_{\mathrm{RMVI},q} \mathbf{x}_\mathrm{I} +\mathbf{v}} \right) }_{=\mathbf{i}_{\mathrm{RMV}{}\hbox {,}q} }. \end{aligned}$$
(30)

With (30), the expected SINR formulation in the user-wise detection can be expressed as

$$\begin{aligned} \hbox {SINR}_{\mathrm{RMV},q} =\frac{E\left\{ {\left\| {\mathbf{W}_{\mathrm{RMV},q}^H \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q}\mathbf{x}_q}\right\| _F^2}\right\} }{E\left\{ {\left\| {\mathbf{i}_{\mathrm{RMV},q}}\right\| _F^2}\right\} }, \end{aligned}$$
(31)

where signal power with \(\mathbf{B}_q^H\mathbf{H}_q\mathbf{P}_q =\mathbf{0}\) can be expressed as

$$\begin{aligned} E\left\{ {\left\| {\mathbf{W}_{\mathrm{RMV},q}^H \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \mathbf{x}_q}\right\| _F^2}\right\} =Tr\left\{ {\mathbf{W}_{\mathrm{RMV},q}^H \mathbf{H}_q \mathbf{H}_q^H \mathbf{W}_{\mathrm{RMV},q}}\right\} =\left\| {\mathbf{H}_q^H \mathbf{H}_q } \right\| _F^2, \end{aligned}$$
(32)

and the composite interference power [14] can be approximately expressed as

$$\begin{aligned}&E\left\{ {\left\| {\mathbf{i}_{\mathrm{RMV},q}}\right\| _F^2}\right\} =tr\left\{ {E\left( {{\hat{\mathbf{W}}}_{\mathrm{RMV},q}^H \mathbf{R}_{\mathrm{RMVI,}q} {\hat{\mathbf{W}}}_{\mathrm{RMV},q}+\Delta \mathbf{W}_{\mathrm{RMV},q}^H \mathbf{H}_q \mathbf{H}_q^H \Delta \mathbf{W}_{\mathrm{RMV,}q}} \right) } \right\} \nonumber \\&\quad \qquad \qquad \qquad \qquad =tr\left\{ E\left( \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI,}q} \mathbf{W}_{\mathrm{RMV,}q}\right. \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \left. \left. +\,\Delta \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI,}q} \Delta \mathbf{W}_{\mathrm{RMV,}q}+\Delta \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{H}_q \mathbf{H}_q^H \Delta \mathbf{W}_{\mathrm{RMV,}q} \right) \right\} \nonumber \\&\quad \qquad \qquad \qquad \qquad \approx tr\left\{ \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI,}q} \mathbf{W}_{\mathrm{RMV,}q} +E\left( {\Delta \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI,}q} \Delta \mathbf{W}_{\mathrm{RMV,}q} } \right) \right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \left. +\frac{N_q \sigma _e^2 }{P}\left\{ tr\left( {\mathbf{H}_q^H \mathbf{H}_q +\mathbf{A}_{\mathrm{RMV},q}^H \mathbf{A}_{\mathrm{RMV},q} }\right. \right\} \right. , \end{aligned}$$
(33)

where \(tr\{E(\Delta \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{R}_{\mathrm{RMVI,}q} \Delta \mathbf{W}_{\mathrm{RMV,}q} )\}\) is expressed in “Appendix C” by using (29) and we have \(\Delta \mathbf{W}_{\mathrm{RMV,}q}^H \mathbf{H}_q \mathbf{P}_{\mathrm{RMV},q} \approx (\Delta \mathbf{H}_{q}\mathbf{P}_{\mathrm{RMV},q}-\mathbf{B}_{\mathrm{RMV},q}\Delta \mathbf{A}_{\mathrm{RMV},q}-\Delta \mathbf{B}_{\mathrm{RMV},q} \mathbf{A}_{\mathrm{RMV},q})^{H} \mathbf{H}_{q}\mathbf{P}_{\mathrm{RMV},q}\) on computing the last term of right hand side (RHS) of (33) due to the neglect of \(\Delta \mathbf{B}_{\mathrm{RMV},q}\Delta \mathbf{A}_{\mathrm{RMV},q}\) by applying the first-order approximation for \(\Delta \mathbf{A}_{\mathrm{RMV},q}={\hat{\mathbf{A}}}_{\mathrm{RMV,}q}-\mathbf{A}_{\mathrm{RMV},q}\). According to (31), the average SINR formulation is

$$\begin{aligned} \hbox {SINR}_{\mathrm{RMV, avg}} =\frac{1}{Q}\sum _{q=1}^Q {\hbox {SINR}_{\mathrm{RMV,}q}}. \end{aligned}$$
(34)

When variance of CSI estimation error is given, this derived formulation in (34) can well predict the ability of interference cancellation in the proposed robust transceiver design due to the realization of the actual SINR tendency obtained by (30) as confirmed in following simulation tests. Moreover, we will show that the proposed RMV-based scheme has better SINR than the MV-based scheme as follows.

Property 2

For giving a precoder \(\mathbf{P}_{q} \in {\mathcal {F}}\), we have \(\hbox {SINR}_{\mathrm{RMV},q} \ge \hbox {SINR}_{\mathrm{MV},q}\) since \(||\mathbf{i}_{\mathrm{MV,}q}||_F^2 \ge ||\mathbf{i}_{\mathrm{RMV,}q}||_F^2\).

Proof

See “Appendix D;;.

3.4 Computational Complexity

In this subsection, the computational complexities [21] of MV-based, RMV-based and conventional SVD-assisted detection schemes at [6] in the precoded UL MU-MIMO systems are investigated for transmitter and receiver separately. For transmitter, it only requires multiplying the symbol vector by the precoding matrix computed by receiver via an error-free feedback link as depicted in (23)-(24), which involves a complexity of \(\sum _{q=1}^Q{N_q^2}\) showed in Table 2. For receiver, Table 2 demonstrates that the complexities of MV-based and RMV-based systems in terms of complex multiplications are computed by following S.3 \(\sim \) S.8 of Table 1, where RMV-based scheme has similar computational complexity compared with MV-based scheme excepting the robust design on S.7 depicted in (5) and (19). Considering the codebook size is \(N_{P}\), it also shows that the proposed RMV-based scheme requires additional \(Q\cdot N_{P}\cdot {\mathcal {O}}(M_r^3)\) multiplications compared with conventional SVD-assisted detection due to the involvement of the robust design in \(\hbox {S}.5\sim \hbox {S}.8\). However, when \(N_{P}\) is small in practical implementation, this additional complexity can be neglected since \(M_{r}\) and \(M_{t}\) are consequently limited in the UL LTE system [5] and thus the proposed RMV approach is a computationally-efficient convex optimization problem to avoid the exhaustive search in the optimization problem depicted in [22].

Table 2 Computational complexities of UL MU-MIMO precoding systems
Full size table

4 Simulation Results

This section uses the proposed RMV-based, MV-based and conventional SVD-assisted detection schemes in [6] to illustrate the bit error rate (BER) in the precoded UL MU-MIMO system, where RMV-based and MV-based detection schemes are established in Table 2. It is assumed that the elements of each channel matrix are \(i.i.d.\) complex Gaussian random variable with zero mean and unit variance [22, 23] as depicted in (1). The LS technique is considered for the CSI estimation and the input SNR is defined as \(P/\sigma _v^2\). The robust design with performance analysis is also examined on theoretic analysis (i.e., theoretic) and computer simulation analysis (i.e., simulation) [24–26]. Furthermore, we consider the proposed schemes with \(N_{t},\,M_{r} \in \{4,6\}, N_{2}\in \{2,4\}, N_{1}=Q = 2, P =N_{t}\) and QPSK modulation where codebooks are created by p.157 and p.159 in [5] for \(N_{2}=2\) and \(N_{2}=4\), respectively to evaluate (A) Selection of the DL factor (B) SINR performance and (C) Comparison with conventional works as following simulations.

4.1 Selection of the DL Factor

In this subsection, various DL factors (i.e., \(\gamma \)) are considered to verify the ability of the proposed RMV-based detection to resist the effect of the imperfect CSI. The proposed RMV-based DL factor is given as

$$\begin{aligned} \gamma =u\cdot \left( {\frac{N_q \sigma _e^2 }{P}+\frac{N_q \sigma _e^2 }{P}tr\left( {{\hat{\mathbf{H}}}_q^{\dagger } {\hat{\mathbf{R}}}_{\mathrm{I},q} \left( {{\hat{\mathbf{H}}}_q^{\dagger } } \right) ^{H}} \right) } \right) , \end{aligned}$$
(35)

where \(u\) is an adaptive factor to adapt various values of \(\gamma \) to validate an optimum selection of the DL factor of (28). Moreover, a conventional DL design with \(\gamma =5\sigma _v^2\) in [17, 18] is given as

$$\begin{aligned} \gamma =u\cdot 5\sigma _v^2. \end{aligned}$$
(36)

With \(\hbox {SNR} = 30 \hbox {dB}\) for \(N_{t}=M_{r} = 4,\,N_{1}=N_{2}=Q=2\), \(u \in \{0,0.01,0.1,1,10,100, 1000,10000\}\), \(\sigma _e^2 =0.01\) and QPSK modulation, Fig. 2a demonstrates that the proposed RMV-based DL factor with \(u=1\) at (35) in the proposed user-wise detection has optimum BER performance compared with others due to the robust design on optimization problem in (12) depicted in Property 1. Similarly, with different number of transmit and receive antennas as \(N_{t}=M_{r}=6,\,N_{1}=2,\,N_{2}=4,\,Q=2\), Fig. 2b also confirms that the proposed RMV-based weighting matrix (i.e., \(u=1\)) can regularize the selection of DL factor optimally in the proposed user-wise detection. Additionally, the conventional DL design with \(\gamma =5\sigma _v^2\) can not regularize the selection of DL factor at \(u = 1\) in the proposed user-wise detection to achieve optimum BER performance by comparing with Fig. 2a, b, respectively. Figures also show that BER performance in the proposed user-wise detection for \(u \in \{0,10000\}\) is worse due to the involvement of the singular problem.

Fig. 2
figure 2

BER comparison for various DL factors in the proposed user-wise detection with \(\sigma _e^2=0.01,\,\hbox {SNR} = 30\,\hbox {dB}\) and QPSK modulation. a \(N_{t}=M_{r}= 4,\,N_{1}=N_{2}=Q = 2\); b \(N_{t}=M_{r} = 6,\,N_{1}= 2,\,N_{2}= 4,\,Q = 2\)

Full size image

4.2 SINR Performance

In this simulation, different variances of CSI estimation error with \(\sigma _e^2 \in \{0,\,0.001,\,0.01\}\) are considered to illustrate the SINR performance of the proposed RMV-based MU-MIMO precoding by using theoretic analysis in (34) and the computer simulation analysis (i.e., actual solution). With \(N_{t}=M_{r}=4,\,N_{1}=N_{2}=Q=2\) and QPSK modulation, Fig. 3a shows that the SINR performance of the proposed theoretic analysis (i.e., Theoretic) can achieve the SINR performance of the simulation analysis (i.e., Simulation) in both perfect and imperfect CSI estimation. This demonstrates that the proposed theoretic analysis can effectively predict the performance of actual SINR, and it also shows that the SINR value is increased at small CSI estimation error resulted from the smaller interference depicted in (31). Moreover, this SINR tendency, increasing SNR induced by increasing SINR, confirms that the proposed robust design can well suppress the effect of MUI and noise. This suppression is also confirmed in Fig. 3b under the consideration of \(N_{t}=M_{r}=6,\,N_{1}=2,\,N_{2}=4,\,Q=2\) and QPSK modulation. With computer simulation to compute the SINR performance, Fig. 4 shows that the proposed RMV-based scheme has better SINR performance than MV-based scheme under considering various CSI error variances (i.e., \(\sigma _e^2\)) in \(\hbox {SNR} = 30\,\hbox {dB}\), due to the involvement the information of the CSI error variance in the optimization problem of (12) depicted in Property 2.

Fig. 3
figure 3

SINR versus SNR by using theoretic analysis and simulation analysis in QPSK modulation and \(\sigma _e^2\in \{0, 0.001, 0.01\}\). a \(N_{t}=M_{r} = 4,\,N_{1}=N_{2}=Q= 2\); b \(N_{t}=M_{r} = 6,\,N_{1}= 2,\,N_{2}= 4\) and \(Q=2\)

Full size image
Fig. 4
figure 4

SINR versus CSI error variance for comparison of MV-based and RMV-based UL MU-MIMO precoding in QPSK modulation and \(\hbox {SNR} = 30\,\hbox {dB}\). a \(N_{t}=M_{r} = 4,\,N_{1}=N_{2}=Q= 2\); b \(N_{t}=M_{r} = 6,\,N_{1}= 2,\,N_{2}= 4\) and \(Q=2\)

Full size image

4.3 Comparison of Conventional Works

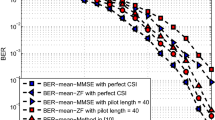
In this subsection, we compare the BER performance of the proposed RMV-based and MV-based with that of the conventional SVD-assisted detection [6] schemes for the perfect and imperfect CSI estimation cases. With \(N_{t}=M_{r}=4,\,N_{1}=N_{2}=Q=2\) and QPSK modulation for perfect CSI estimation, Fig. 5a shows that the proposed RMV-based and MV-based detection schemes have better detection performance than conventional SVD-assisted detection schemes in [6], due to the optimum design of adaptive and precoder matrices jointly in (7) and (21) to resist the effect of MUI and noise. Figure 5a also shows that the RMV-based scheme is an unbiased design due to the involvement of the same BER performance compared with the MV-based scheme depicted in (26). For imperfect CSI estimation, Fig. 5b, c demonstrates that the proposed RMV-based detection substantially outperforms others particularly at high SNR region confirmed in Fig. 4 and Property 2. Similarly, with \(N_{t}=M_{r}= 6,\,N_{1}= 2,\,N_{2}=4,\,Q=2\) and QPSK modulation, Fig. 6 also demonstrates that the proposed RMV-based scheme can effectively improve the detection performance in the precoded UL MU-MIMO transmission compared with others.

Fig. 5
figure 5

BER versus SNR with \(N_{t}=M_{r} = 4,\,N_{1}=N_{2}=Q = 2\) and QPSK modulation for comparison of various detection schemes. a \(\sigma _e^2 =0\), b \(\sigma _e^2 =0.001\); c \(\sigma _e^2 =0.01\)

Full size image
Fig. 6
figure 6

BER versus SNR with \(N_{t}=M_{r}=6,\,N_{1}= 2,\,N_{2}=4,\,Q=2\) and QPSK modulation for comparison of various detection schemes. a \(\sigma _e^2 =0\), b \(\sigma _e^2 =0.001\); c \(\sigma _e^2 =0.01\)

Full size image

5 Conclusions

In this paper, we have presented a robust transceiver design with joint suppression of effect of MUI, noise and CSI estimation error in UL MU-MIMO precoding for limited feedback system under considering LS technique on CSI estimation. Since robust transceiver design is difficult to be tractable, the optimization problem with considering design of the precoder and adaptive matrices on the constrained MV approach subjects to constraint the rejection of CSI estimation error developed in the use-wise detection. To validate this user-wise detection for robustness specifically, the performance analysis of robust transceiver design induced by mean characteristic, regularization of the DL factor, SINR formulation and computational complexity has been investigated. In both perfect and imperfect CSI estimation, simulations verify that the proposed RMV-based transceiver design can achieve optimal detection performance due to optimizing design of precoder and adaptive matrices jointly. Therefore, the proposed RMV-based transmission design is a promising solution for practical UL MU-MIMO precoding in limited feedback wireless systems at the mobile station is of major concerns.