Abstract
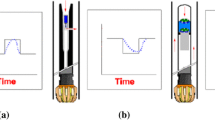
Wireless mud-logging systems have been employed in petroleum exploration to guarantee efficiency and safety in well-drilling. For the wireless networks in well-drillings, the tradeoff between throughput and fairness has great relation to the type of wells. The throughput is of the most importance to deep wells, while fairness is of primary concern for shallow wells. In this study, this challenge is addressed by using 2-SIC (successive interference cancellation) techniques. The throughput maximization and the fairness maximization problems are further formulated based on an imperfect 2-SIC model, which differentiates our work from existing ones. In view of the hardness of these problems, a low-complexity approximation algorithm for maximizing throughput and a low-complexity heuristic algorithm for maximizing fairness are proposed. To evaluate the proposed schemes, extensive simulations are performed. According to simulation results, the throughput performance could be improved by 23% using our approximation algorithm of throughput maximization, while the Jain’s fairness index could reach 0.975 using our algorithm of fairness optimization.











Similar content being viewed by others
Notes
\(p_{max}\) can be regarded as the maximal allowable transmit power under the energy budget instead of the maximal transmit power which is bounded by the hardware. It can be set dynamically.
Decoding priority can be random if \({G_i}{p_i}={G_j}{p_j}\).
The lemma can be generalized to the throughput maximization problem with more than two transmitters. The conclusion coincides with [8], where perfect SIC is considered.
References
Han, G., Jiang, J., Zhang, C., Duong, T. Q., Guizani, M., & Karagiannidis, G. (2016). A survey on mobile anchors assisted localization in wireless sensor networks. IEEE Communications Surveys Tutorials, 18(3), 2220–2243.
Xie, R., Liu, A., & Gao, J. (2016). A residual energy aware schedule scheme for WSNs employing adjustable awake/sleep duty cycle. Wireless Personal Communications, 90(4), 1859–1887.
Zhang, X. C., & Haenggi, M. (2014). The performance of successive interference cancellation in random wireless networks. IEEE Transactions on Information Theory, 60(10), 6368–6388.
Karipidis, E., Yuan, D., He, Q., & Larssonv, E. G. (2015). Max–min power allocation in wireless networks with successive interference cancellation. IEEE Tranactions on Wireless Communications, 14(11), 6269–6282.
Yuan, D., Vangelis, A., Lei, C., Eleftherios, K., & Larsson, G. E. (2013). On optimal link activation with interference cancellation in wireless networking. IEEE Transactions on Vehicular Technology, 62(2), 939–945.
Zhiguo, D., Pingzhi, F., & Poor, H. V. (2016). Impact of user pairing on 5g nonorthogonal multiple-access downlink transmissions. IEEE Transactions on Vehicular Technology, 65(8), 6010–6023.
Zheng, Y., Zhiguo, D., Pingzhi, F., & Dhahir, N. A. (2016). A general power allocation scheme to guarantee quality of service in downlink and uplink noma systems. IEEE Transactions on Wireless Communications, 15(11), 7244–7257.
Lei, L., Yuan, D., Chin, K. H., & Sumei, S. (2016). Power and channel allocation for non-orthogonal multiple access in 5g systems: Tractability and computation. IEEE Transactions on Wireless Communications, 15(12), 8580–8594.
Xu, C., Li, P., & Ci, S. (2013). Decentralized power allocation for random access with successive interference cancellation. IEEE Journal on Selected Area in Communications, 31(11), 2387–2396.
Mollanoori, M., & Ghaderi, M. (2014). Uplink scheduling in wireless networks with successive interference cancellation. IEEE Transactions on Mobile Computing, 13(5), 1132–1144.
Sung, C. W. & Fu, Y. (2016). A game-theoretic analysis of uplink power control for a non-orthogonal multiple access system with two interfering cells. In Proceedings of the 83rd IEEE vehicular technology conference (VTC Spring) (pp. 1–5), May 2016, Nanjing, China. IEEE.
Agrawal, A. (2003). Power control for space-time multiuser CDMA. PhD thesis, Stanford University.
Green, D. B., & Obaidat, A. S. (2002). An accurate line of sight propagation performance model for ad hoc 802.11 wireless LAN (WLAN) devices. In Proceedings of the IEEE international conference on communications (pp. 3424–3428), New York, USA, April 2002. IEEE.
Oliveto, P. S., He, J., & Xiao, X. (2007). Time complexity of evolutionary algorithms for combinatorial optimization: A decade of results. International Journal of Automation and Computing, 4(3), 281–293.
Jiang, C., Shi, Y., Hou, Y. T., Lou, W., Kompella, S., & Midkiff, S. F. (2012). Squeezing the most out of interference: An optimization framework for joint interference exploitation and avoidance. In Proceedings of the 31th IEEE InfoCom (pp. 424–432), Orlando, USA, March 2012. IEEE.
Karipidis, E., Yuan, D., He, Q., & Larsson, E. G. (2015). Max–min power control in wireless networks with successive interference cancellation. IEEE Transactions on Wireless Communication, 14(11), 6269–6282.
Yu, Y., Huang, S., Wang, J., & Ou, J. (2015). Design of wireless logging instrument system for monitoring oil drilling platform. IEEE Sensors Journal, 15(6), 3453–3458.
Collotta, M., Gentile, L., Pau G., & Scat, G. (2012). A dynamic algorithm to improve industrial wireless sensor networks management. In Proceedings of 38th annual conference of the IEEE Industrial Electronics Society (pp. 2802–2807), Montreal, Canada, October 2012. IEEE.
Acknowledgements
This work was supported by National Natural Science Foundation of China (61173132), Science Foundation of China University of Petroleum, Beijing (ZX20150089).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proving Theorem 1
Lemma 5
If\((p_i^*,p_j^*)\)is the optimal solution of PCMT-TN, then\(p_i^*=p_{max}\)or\(p_j^*=p_{max}\).
Proof
Assume there is a feasible solution \(({p_i'},{p_j'})\). If \({p_i'}\ge {p_j'}\), \((k{p_i'},k{p_j'})\) is still feasible for all \(0<k \le \frac{p_{max}}{p_i'}\). Besides, \(Th_{i,j}(k{p_i'},k{p_j'})\) is an increasing function of k. So, the optimal solution satisfies \(p_i^*=p_{max}\). Similarly, If \({p_i'}<{p_j'}\), the optimal solution satisfies \(p_j^*=p_{max}\).\(\square\)
Proof of Theorem 1
Case 1 Assume \(p_j^*=p_{max}\)
In this case, PCMT-TN problem is actually
It can be known that
Since \({\frac{{dTh_{i,j}({p_i,p_{max}})}}{dp_i}} > 0\) for all \({p_i} \ge \frac{{{G_j}{p_{\max }}}}{{{G_i}}}\). \(T{h_{i,j}}\left( {{p_i},{p_{\max }}} \right)\) will increase with increasing \(p_i\) if \({p_i} \ge \frac{{{G_j}{p_{\max }}}}{{{G_i}}}\). Thus, the maximum is achieved when \(p_i=p_{max}\), and the maximum throughput is \(T{h_{i,j}}\left( {{p_{\max }},{p_{\max }}} \right)\).
In conclusion, under Cases 1, the solution is always \((p_{max},p_{max})\).
Case 2 Assume \(p_j^*<p_{max}\)
In this case, \(p_i^*=p_{max}\), thus, PCMT-TN problem is
In Case 2, we further divide the problem into two subcases, i.e., Cases 2.1 and 2.2.
Case 2.1 \(\sqrt{\varepsilon }{G_i}{p_{\max }} - {N_0} \le 0\). Since
it can be seen that \(\frac{dTh_{i,j} (p_{max},p_j)}{dp_j} \ge 0\) for any \(p_j \in [0,p_{max})\). Therefore, the optimal solution in this case is \((p_{max},p_{max}-\delta )\), where \(\delta\) is a sufficiently small positive number.
Since the optimal solution in Case 1 is \((p_{max},p_{max})\), the optimal solution is \((p_{max},p_{max})\) if \(\sqrt{\varepsilon }{G_i}{p_{\max }} - {N_0} \le 0\).
Case 2.2 \(\sqrt{\varepsilon }{G_i}{p_{\max }} - {N_0} > 0\). Note that
In Case 2.2, we further divide the problem into two cases: Cases 2.2.1 and 2.2.2.
Case 2.2.1 If \((\sqrt{\varepsilon } G_i p_{max}-N_0)/G_j \ge p_{max}\), i.e., \(p_{max} \ge \ N_0/(\sqrt{\varepsilon } G_i-G_j)\). At this time, \(Th_{i,j}(p_{max},p_j)\) is shown in Fig. 12(a). Obviously, the optimal solution is obtained when \(p_j=0\), i.e., the optimal solution in this case is \((p_{max},0)\).
Case 2.2.2 If \(p_{max}<N_0/(\sqrt{\varepsilon } G_i-G_j )\), \(Th_{i,j}(p_{max},p_j)\) in Case 2.2.2 is shown in Fig. 12(b). Obviously, the optimal solution is either \((p_{max},p_{max})\) or \((p_{max},0)\). Specifically, if \(Th_{i,j}(p_{max},p_{max}) \ge Th_{i,j}(p_{max},0)\), the optimal solution is \((p_{max},p_{max})\), and it is \((p_{max},0)\) otherwise. \(\square\)
Appendix 2: Proving Theorem 2
Lemma 6
The optimal solution\((p_i^*,p_j^*)\)for PCMF-TN satisfies\(p_i^*=p_{max}\)or\(p_j^*=p_{max}\).
Proof
The proof is similar with that of Lemma 5.\(\square\)
Lemma 7
The optimal solution\((p_i^*,p_j^*)\)for PCMF-TN is shown in (11), where\({{\widehat{p}}_i} = \frac{{\sqrt{{N_0}^2 + 4\varepsilon {G_j}^2{p_{\max }}^2 + 4{N_0}\varepsilon {G_j}{p_{\max }}} - {N_0}}}{{2\varepsilon {G_i}}}\), \({{\widehat{p}}_j} = \frac{{\sqrt{{N_0}^2 + 4\varepsilon {G_i}^2{p_{\max }}^2 + 4{N_0}{G_i}{p_{\max }}} - {N_0}}}{{2{G_j}}}\), and \(F{a_{i,j}}\left( {{p_i},{p_j}} \right) = \min \left( {1 + \frac{{{G_i}{p_i}}}{{{G_j}{p_j} + {N_0}}},1 + \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_i} + {N_0}}}} \right)\).
Proof
Based on Lemma 6, two possibilities of the optimal solution of PCMF-TN are discussed separately and then merged as follows:
Case 1 Assume \(p_i^*=p_{max}\)
In this case, PCMF-TN problem is actually formulated as follows:
Since \({{\widehat{p}}_j}=\frac{{\sqrt{{N_0}^2 + 4\varepsilon {G_i}^2{p_{\max }}^2 + 4{N_0}{G_i}{p_{\max }}} - {N_0}}}{{2{G_j}}}\), it can be easily verified that \(\frac{{{G_i}{p_{\max }}}}{{{G_j}{{{\widehat{p}}}_j} + {N_0}}} = \frac{{{G_j}{{{\widehat{p}}}_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}\).
Case 1.1 \({{\widehat{p}}_j}<p_{max}\)
Case 1.1.1 For any \(p_j \in [0,{{\widehat{p}}_j})\),
since \(\frac{{{G_i}{p_{max }}}}{{{G_j}{p_j} + {N_0}}}> \frac{{{G_i}{p_{max}}}}{{{G_j}{{{\widehat{p}}}_j} + {N_0}}} = \frac{{{G_j}{{{\widehat{p}}}_j}}}{{\varepsilon {G_i}p_{max}+N_0}} > \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{max}} + N_0}}\), \(Fa_{i,j}({{p_{max}},{p_j}}) = min \left( {1 + \frac{{{G_i}{p_{max}}}}{{{G_j}{p_j} + {N_0}}},1 + \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{max}} + {N_0}}}}\right) = 1 + \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{max}} + {N_0}}} < 1 + \frac{{{G_j}{{{\widehat{p}}}_j}}}{{\varepsilon {G_i}{p_{max}} + {N_0}}} = F{a_{i,j}}({{p_{max}},{{{\widehat{p}}}_j}}).\)
Case 1.1.2 For any \(p_j \in ({{\widehat{p}}_j},p_{max}]\), since \(\frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}> \frac{{{G_j}{{{\widehat{p}}}_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}} = \frac{{{G_i}{p_{\max }}}}{{{G_j}{{{\widehat{p}}}_j} + {N_0}}} > \frac{{{G_i}{p_{\max }}}}{{{G_j}{p_j} + {N_0}}}\),
In conclusion, for Case 1.1, the optimal solution for PCMF-TN is \((p_{max},{{{\widehat{p}}}_j})\).
Case 1.2 \({{\widehat{p}}_j} \ge p_{max}\)
It can be proved that for all \(p_j \in [0,{{\widehat{p}}}_j]\), \(\frac{{{G_i}{p_{max}}}}{{{G_j}{p_j} + {N_0}}} \ge \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}\) is true. Its proof is as follows: Obviously, \(p_j \in [0,{{{\widehat{p}}}_j]}\), \(\frac{{{G_i}{p_{max}}}}{{{G_j}{p_j} + {N_0}}} \ge \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}\) is equivalent to \({G_j}^2{p_j}^2 + {N_0}{G_j}{p_j} - \varepsilon {G_i}^2{p_{\max }}^2 - {N_0}{G_i}{p_{\max }} \le 0\). For any \(p_j \in [0,{{\widehat{p}}_j}]\), the latter inequality above is true by following the property of quadratic functions.
Since \(p_{max} \in [0,{{\widehat{p}}_j}]\), it follows \(\frac{{{G_i}{p_{\max }}}}{{{G_j}{p_{\max }} + {N_0}}} \ge \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}\).
For any \(p_j \in [0,p_{max})\), we can obtain that \(F{a_{i,j}}\left( {{p_{\max }},{p_j}} \right) = min\left( {1 + \frac{{{G_i}{p_{\max }}}}{{{G_j}{p_j} + {N_0}}},1 + \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}} \right) = 1 + \frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}< 1 + \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}} = F{a_{i,j}}\left( {{p_{\max }},{p_{\max }}} \right)\), owing to \(\frac{{{G_j}{p_j}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}< \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}} \le \frac{{{G_i}{p_{\max }}}}{{{G_j}{p_{\max }} + {N_0}}} < \frac{{{G_i}{p_{\max }}}}{{{G_j}{p_j} + {N_0}}}\).
In conclusion, the optimal solution for PCMF-TN is \((p_{max},p_{max})\) for Case 1.2. Therefore, we can know that the optimal solution for PCMF-TN is \((p_{max},min(p_{max},{{\widehat{p}}_j}))\) in Case 1.
Case 2 Assume \(p_j^*=p_{max}\)
In this case, PCMF-TN problem can be formulated as follows:
Since \({{\widehat{p}}_i} = \frac{{\sqrt{{N_0}^2 + 4\varepsilon {G_j}^2{p_{max }}^2 + 4{N_0}\varepsilon {G_j}{p_{max}}} - {N_0}}}{{2\varepsilon {G_i}}}\), it can be easily verified that \(\frac{{{G_i}{{{\widehat{p}}}_i}}}{{{G_j}{p_{max }} + {N_0}}} = \frac{{{G_j}{p_{max }}}}{{\varepsilon {G_i}{{{\widehat{p}}}_i} + {N_0}}}\).
Case 2.1 \({{\widehat{p}}_i}<p_{max}\)
Case 2.1.1 For any \(p_i \in [0,{{\widehat{p}}}_i]\), since \(\frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}}< \frac{{{G_i}{{{\widehat{p}}}_i}}}{{{G_j}{p_{\max }} + {N_0}}} = \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{{{\widehat{p}}}_i} + {N_0}}} < \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_i} + {N_0}}}\), \(F{a_{i,j}}\left( {{p_i},{p_{\max }}} \right) = \min \left( {1 + \frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}},1 + \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_i} + {N_0}}}} \right) = 1 + \frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}} < 1 + \frac{{{G_i}{{{\widehat{p}}}_i}}}{{{G_j}{p_{\max }} + {N_0}}} = F{a_{i,j}}\left( {{{{\widehat{p}}}_i},{p_{\max }}} \right).\)
Case 2.1.2 For any \(p_i \in [{{\widehat{p}}}_i, p_{max}]\), since \(\frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}}> \frac{{{G_i}{{{\widehat{p}}}_i}}}{{{G_j}{p_{\max }} + {N_0}}} = \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{{{\widehat{p}}}_i} + {N_0}}} > \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_i} + {N_0}}},\)
In conclusion, for Case 2.1, the optimal solution for PCMF-TN is \(({{{\widehat{p}}}_i},p_{max})\).
Case 2.2 \({{{\widehat{p}}}_i} \ge p_{max}\)
Just as that in Case 1.2, it can be easily verified that for any \(p_i \in [0, {{{\widehat{p}}}_i}]\), \(\frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}} \le \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_i} + {N_0}}}\). Since \(p_{max} \in [0,{{{\widehat{p}}}_i}]\), we can thus get \(\frac{{{G_i}{p_{\max }}}}{{{G_j}{p_{\max }} + {N_0}}} \le \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_{\max }} + {N_0}}}\).
For any \(p_i \in [0, p_{max})\), since \(\frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}}< \frac{{{G_i}{p_{\max }}}}{{{G_j}{p_{\max }} + {N_0}}} \le \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_{max}} + {N_0}}} < \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_i} + {N_0}}},\) we can know that \(F{a_{i,j}}\left( {{p_i},{p_{\max }}} \right) = \min \left( {1 + \frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}},1 + \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{p_i} + {N_0}}}} \right) = 1 + \frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}}=1 + \frac{{{G_i}{p_i}}}{{{G_j}{p_{\max }} + {N_0}}} < 1 + \frac{{{G_i}{p_{\max }}}}{{{G_j}{p_{\max }} + {N_0}}} = F{a_{i,j}}\left( {{p_{\max }},{p_{\max }}} \right).\)
In conclusion, for Case 2.2, the optimal solution for PCMF-TN is \((p_{max},p_{max})\). So, for Case 2, the optimal solution for PCMF-TN is \((min(p_{max},{{{\widehat{p}}}_i}),p_{max})\).
Combining Case 1 with Case 2, we thus get Formula (11). We now try to find \(min({{{\widehat{p}}}_j},p_{max})\) and \(min({{{\widehat{p}}}_i},p_{max})\) to get a brief expression for the optimal solution to PCMF-TN.\(\square\)
Lemma 8
If\(\left( {\left( {{p_{\max }} \ge \frac{{{N_0}\left( {{G_i} - {G_j}} \right) }}{{{G_j}^2 - \varepsilon {G_i}^2}}} \right) \wedge \left( {\sqrt{\varepsilon }{G_i}< {G_j} < {G_i}} \right) } \right) \vee \left( {{G_j} = {G_i}} \right)\), then\(\min \left( {{{{\widehat{p}}}_i},{p_{\max }}} \right) = {p_{\max }}\)and\(\min \left( {{{{\widehat{p}}}_j},{p_{\max }}} \right) = {{{\widehat{p}}}_j}\). \(min({{{{\widehat{p}}}_i},{p_{max }}}) = {{{\widehat{p}}}_i}\)and\(min({{{\widehat{p}}}_j},{p_{max}}) = {p_{max}}\)in all other cases,.
Proof
Since \({{{\widehat{p}}}_i} = \frac{{\sqrt{{N_0}^2 + 4\varepsilon {G_j}^2{p_{\max }}^2 + 4{N_0}\varepsilon {G_j}{p_{\max }}} - {N_0}}}{{2\varepsilon {G_i}}} < {p_{\max }}\) is equivalent with the inequation \(\left( {{G_j}^2 - \varepsilon {G_i}^2} \right) {p_{\max }} < {N_0}({G_i} - {G_j})\), it naturally results in Formula (12). \(\square\)
Similarly, we can get Formula (13).
So, if \(\left( {\left( {{p_{\max }} \ge \frac{{{N_0}\left( {{G_i} - {G_j}} \right) }}{{{G_j}^2 - \varepsilon {G_i}^2}}} \right) \wedge \left( {\sqrt{\varepsilon }{G_i}< {G_j} < {G_i}} \right) } \right) \vee \left( {{G_j} = {G_i}} \right)\) holds, \(\min \left( {{{{\widehat{p}}}_i},{p_{\max }}} \right) = {p_{\max }}\) and \(\min \left( {{{{\widehat{p}}}_j},{p_{\max }}} \right) = {{\widehat{p}}_j}\). Otherwise \(\min \left( {{{{\widehat{p}}}_i},{p_{\max }}} \right) = {{\widehat{p}}_i}\) and \(\min \left( {{{{\widehat{p}}}_j},{p_{\max }}} \right) = {p_{\max }}\).
Proof of Theorem 2
From Lemmas 7 and 8, if \(\left( {\left( {{p_{\max }} \ge \frac{{{N_0}\left( {{G_i} - {G_j}} \right) }}{{{G_j}^2 - \varepsilon {G_i}^2}}} \right) \wedge \left( {\sqrt{\varepsilon }{G_i}< {G_j} < {G_i}} \right) } \right) \vee \left( {{G_j} = {G_i}} \right),\)\(( {p_i^*,p_j^*}) = argmax({F{a_{i,j}}( {{p_{\max }},{p_{\max }}} ), F{a_{i,j}}( {{p_{\max }},{{{\widehat{p}}}_j}} )} )\) where \({{{\widehat{p}}}_j} \le {p_{\max }}\). Based on Formula (10), \(F{a_{i,j}}( {{p_{\max }},{{{\widehat{p}}}_j}} )\) is greater than \(F{a_{i,j}}( {{p_{\max }},{p_{\max }}} )\) and \(F{a_{i,j}}( {{p_{\max }},{{{\widehat{p}}}_j}} ) = 1 + \frac{{{G_i}{p_{\max }}}}{{{G_j}{{{\widehat{p}}}_j} + {N_0}}}\).
\((p_i^*,p_j^* )=argmax( {F{a_{i,j}}( {{{{\widehat{p}}}_i},{p_{\max }}} ), F{a_{i,j}}( {{p_{\max }},{p_{\max }}} )} )\) holds in all other cases, where \({{{\widehat{p}}}_i} \le {p_{\max }}\). Based on Formula (14), \(F{a_{i,j}}( {{{{\widehat{p}}}_i},{p_{\max }}} )\) is greater than \(F{a_{i,j}}( {{p_{\max }},{p_{\max }}} )\) and \(F{a_{i,j}}( {{{{\widehat{p}}}_i},{p_{\max }}} ) = 1 + \frac{{{G_j}{p_{\max }}}}{{\varepsilon {G_i}{{{\widehat{p}}}_i} + {N_0}}}\).
Theorem 2 is thus proved by substituting above results into Formula (11). \(\square\)
Rights and permissions
About this article
Cite this article
Xu, C., Ding, H. & Xu, Y. Low-complexity uplink scheduling algorithms with power control in successive interference cancellation based wireless mud-logging systems. Wireless Netw 25, 321–334 (2019). https://doi.org/10.1007/s11276-017-1561-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-017-1561-7