Lubrication–Contact Interface Conditions and Novel Mixed/Boundary Lubrication Modeling Methodology

Abstract

Under severe conditions, solid contacts take place even when parts are lubricated. Precise mathematical conditions are needed to describe the interior interface between fluid lubrication and solid-contact zones. In order to distinguish the conditions for this interface from conventional lubrication boundary conditions, they are named lubrication–contact interface conditions (LCICs). In this work, mathematical LCICs are derived with local flow continuity from the continuum mechanics point of view and pressure inequality across the interface. Numerical implementations are developed and tested with problems having simple geometries and configurations, and they are integrated into a new mixed/boundary elastohydrodynamic lubrication solver that uses a new method to determine solid-contact pressures. This solver is capable of capturing film thickness and pressure behaviors involving solid contacts.

1 Introduction

Modeling full-film lubrication problems between two solid bodies requires boundary conditions at the inlet, exit, and sides of the lubrication region, or at the interior cavitation boundaries if applicable, for the Reynolds equation to be properly solved. Some of the boundary conditions for fluid exit are summarized by Liu in [1]. Moreover, in real engineering products, mixed/boundary lubrication can occur at low speeds and/or heavy loads, where fluid lubrication exists in some zones while solid contacts appear in other, co-existing in the nominal lubrication region. Solid contacts in this paper mean no effective hydrodynamic lubrication film between the two surfaces. Zapletal et al. [2] measured gaps, or the film thickness, using interferograms, between two lubricated surfaces with different levels of roughness under varying speeds, and quantitatively evaluated the extent of solid contacts. When modeling such lubrication problems using the Reynolds equation, it is necessary to define the conditions that reflect the local physical reality at the interfaces between solid contact on one side of the interface and fluid lubrication on the other. These boundary conditions between the liquid-lubricated and solid-contact zones in the space between the two solid bodies are called the lubrication–contact interface conditions (LCICs), where “contact” refers to solid contact.

Zhu and Wang [3] reviewed the history and progress of elastohydrodynamic lubrication (EHL) simulations, including recent significant accomplishments for relatively thin-film deterministic solutions considering real measured roughness. There are two types of rough-surface EHL models: stochastic [4,5,6,7,8,9,10,11] and deterministic [12,13,14,15,16,17,18,19,20,21,22,23]. Because the stochastic models need separate deterministic sub-models to determine flow factors, deterministic models play a key role in EHL analyses.

In deterministic EHL models, there are two approaches dealing with solid contacts, both using the finite-difference methodology: (1) lubrication and solid-contact zones are treated separately [12,13,14], in which the fluid-film pressure and solid-contact pressure variables are defined, respectively, and they are updated in sequential steps of an iteration process; (2) lubrication and solid-contact zones are treated with a unified system of equations [15,16,17,18,19,20,21], where the pressure variables, i.e., old and new pressure arrays, cover both lubrication and solid-contact zones, and they are updated within the same step in the iteration. In most cases, negative gaps encountered during the fluid pressure iteration were set to zero or a small positive value, as suggested in Appendix B of [4] by Patir.

Chang [12] studied transient line-contact mixed-EHL problems with a deterministic model that set the film thickness to one-thousandth of the central film thickness for the smooth-surface case, h_os, if the calculated film thickness is smaller than h_os. Thus, the fluid-film pressure was obtained from the Reynolds equation for the entire simulation region, and the LCICs were avoided. Jiang et al. [13] presented a transient mixed-EHL model for point-contact problems, and their approach pertaining to the LCICs is that when the film thickness at a node is less than or equal to zero, (a) the film thickness is set to zero; (b) two coefficients for the upstream and downstream nodes need to be updated with zero film thickness; and (c) the fluid pressure is set to the solid-contact pressure. Zhao et al. [14] simulated the start of circular-contact EHL without explicit LCICs but used these constraints (a) the fluid-film lubrication zones had positive film thicknesses, zero solid-contact pressures, and non-negative fluid-film pressure and (b) the solid-contact zones had zero film thicknesses, positive solid-contact pressures, and zero fluid-film pressures. Zhu and Hu [15, 16] introduced the unified equation system, which essentially uses the Reynolds equation for the entire simulation region. This approach is practical and has been successfully applied in their subsequent works and by others [16,17,18,19,20]. Holmes et al. [21] used the Reynolds equation and the elastic deformation equation in a differential form to update unknown nodal values of pressure and film thickness. Once a nodal value of film thickness was negative, it was set to zero and the nodal pressure value was updated with the elastic deflection equation only. Li and Kahraman [22] utilized the unified equation system [15], but discretized it by means of an asymmetric integrated control volume. However, LCICs were ignored in these works [12, 14,15,16,17,18,19,20,21,22]. Deolalikar et al. [23] treated the lubrication and solid-contact zones separately and explicitly applied a no-flow boundary condition to the places where the fluid zones were in the upstream of the solid-contact zones. The unified equation system [15] was also used by Zhang and Zhang [24] as the first step. After a pre-determined number of iterations, if the gap was still less than a threshold, the solid-contact pressure was separately determined by using the gap value, the pressure at the last iteration, and one influence coefficient of deformation. Then zero hydrodynamic pressures were enforced on the lubrication-contact boundaries in order to solve the Reynolds equation for other locations having gaps larger than the threshold. LCICs were dealt with, to some extent, in references [13, 23, 24]. It should be noted that references [12,13,14,15,16,17,18,19,20,21,22,23,24] have successfully used the gap values to determine whether a node is under fluid-film lubrication or solid contact, and thus temporary boundaries between fluid lubrication and solid contacts could be obtained before each iteration. Once the iteration process was completed, this partition became final.

Venner and Lubrecht [25] and Habchi [26] described in detail, in their monographs, how to apply the multigrid method and the finite element method, respectively, to solve EHL problems. Wang and Zhu [27] summarized the mixed lubrication simulation approaches rooted in the finite-difference method. Among others, Liu et al. [28] obtained simulation results using the finite-difference method in good agreement with the experimental data. However, regarding the thin-film and mixed-EHL regimes, Zhu [29] stated that “converged and accurate numerical solutions become difficult, and effects of computational mesh density and differential schemes appear to be more significant. Also, there is currently a debate on how solid contact should be defined and analyzed, and whether it is indeed possible to model solid contact through a grid-converged solution of the EHL equation system.” In fact, these challenges are still open, and most existing simulation works might have either missed or only partially addressed the LCICs, as mentioned above.

Moreover, Hansen et al. [30] proposed a new updated film parameter, and Mohammadpour et al. [31] investigated exterior boundary conditions of point EHL contacts with a combined numerical–experimental analysis. On other fronts, EHL is finding wider applications: Zhou et al. [32] applied EHL simulation to study lubrication between case‑hardened gears; AL-Mayali et al. [33] studied micropitting initiation with experiments and numerical simulations; and Ma et al. [34] implemented a mixed-EHL modeling to explore the formation of superlubricity using glycerol aqueous solutions.

Mixed EHL with proper LCISs becomes a key issue for the precise pressure/film-thickness determination in the mixed/boundary lubrication under the influence of solid contacts. Such a situation motivated recent explorations on LCICs through theoretical analyses. Liu et al. [35] studied the flow continuity in line-contact EHL modeling and revealed a flow-continuity view of the discrete Reynolds equation. Liu [36] derived analytical solutions to several lubrication problems with flow blockages. Qiu et al. [37] investigated the flow continuity in point-contact EHL modeling.

This paper aims at modeling mixed/boundary elastohydrodynamic lubrication problems with proper equations for the LCICs and a new methodology for numerical implementations, together with a new method for contact-pressure determination. It is confined within continuum mechanics to ensure a correct base for understanding EHL problems. The theory and method are verified through solving problems involving simple geometries, under the no-slip and no-cavitation assumptions. The lubrication status of a smooth-surface EHL problem is solved subjected to different entrainment velocities to explore the transition from full-film EHL to full (inside the Hertzian zone) solid contact.

2 Lubrication–Contact Interface Conditions

The interaction of the surfaces of two components may form various interfaces in a mixed or boundary lubrication, namely, the overall interface of these two components, the sub-interfaces between solids (such as asperities) in direct solid contacts, the sub-interface between the lubricant and the surfaces in lubricated zones, and a less discussed kind of sub-interface—the borders of solid contacts which are surrounded by the lubricant. The work reported in this paper mainly deals with the latter—the lubrication–contact interface. This section elaborates the interfacial conditions in a mixed/boundary lubrication problem from the continuum point of view and describes the interface conditions explicitly with mathematical equations and inequalities. This set of LCICs should address two aspects of lubrication: pressure and flow.

2.1 Pressure Conditions

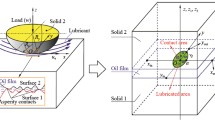
Figure 1a is a typical three-dimensional (3D) representation of the line-contact lubrication problems, for example, in a cam and a follower system or in a pin-disk laboratory configuration. Figure 1b illustrates a cross section perpendicular to the length direction, and the 3D problem becomes a two-dimensional (2D) problem. Interfaces can occur between the fluid lubrication and solid contact. The non-dimensional coordinate of the interface is X_Γ, and on the two sides of the interface, there are fluid pressure ${P}_{\text{f}}$ and solid-contact pressure ${P}_{\text{d}}$. If ${X}_{\Gamma }^{-}$ is for the immediate left side of the interface (or the minus side) and ${X}_{\Gamma }^{+}$ is the immediate right side of it (or the plus side), the non-dimensional pressures are ${P \left({X}_{\Gamma }^{-}\right)=P}_{\text{f}}$ and${P \left({X}_{\Gamma }^{+}\right)=P}_{\text{d}}$. According to the physics of the situation in Fig. 1, the solid-contact pressure to the immediate right of X_Γ should be greater than or equal to the fluid pressure to its immediate left, i.e.,

$$P_{\text{d}} \left( {X_{\Gamma }^{ + } } \right){ } \ge { }P_{\text{f}} \left( {X_{\Gamma }^{ - } } \right)$$

(1)

Fig. 1

A line-contact lubrication problem. a 3D view and b cross-sectional view with lubrication–contact interfaces

In other words, this pressure condition ensures that in order to maintain the solid contact starting at X_Γ, the lubricant pressure there should not surpass the pressure at the solid-contact side. Otherwise, the lubricant would be able to penetrate and open the contact junction before reaching equilibrium.

Figure 2b illustrates lubrication–contact interfaces in a three-dimensional (3D) problem, viewed from the top of the junction. In general, the interface, Γ, has an arbitrary shape, and normal n_Γi is defined for the interface at location Γ_i. The interface conditions can be expressed along the normal. However, for the purpose of numerical modeling where the interfaces are specified with discrete meshes, this normal is either horizontal or vertical in the Cartesian coordinates. It is doubtful that ${P}_{\text{f}} ({X}_{\Gamma })$ on all such interfaces should be zero all the time, as suggested in [23]. Similar to the 2D problem, the solid-contact pressure on the contact side of the interfaces should not be lower than the fluid pressure on the other side. Therefore, the pressure constraints can be expressed in four directions, namely west, east, north, and south,

$$P_{\text{d}} \left( {X_{{\Gamma_{w} }}^{ + } ,Y_{{\Gamma_{w} }} } \right){ } \ge { }P_{\text{f}} \left( {X_{{\Gamma_{w} }}^{ - } ,Y_{{\Gamma_{w} }} } \right)\;{\text{at}}\;\Gamma w$$

(2)

$$P_{\text{d}} \left( {X_{{\Gamma_{e} }}^{ - } ,Y_{{\Gamma_{e} }} } \right){ } \ge { }P_{\text{f}} \left( {X_{{\Gamma_{e} }}^{ + } ,Y_{{\Gamma_{e} }} } \right)\;{\text{at}}\;\Gamma e$$

$$P_{\text{d}} \left( {X_{{\Gamma_{n} }} ,Y_{{\Gamma_{n} }}^{ - } } \right){ } \ge { }P_{\text{f}} \left( {X_{{\Gamma_{n} }} ,Y_{{\Gamma_{n} }}^{ + } } \right)\;{\text{at}}\;\Gamma n$$

$$P_{\text{d}} \left( {X_{{\Gamma_{s} }} ,Y_{{\Gamma_{s} }}^{ + } } \right){ } \ge { }P_{\text{f}} \left( {X_{{\Gamma_{s} }} ,Y_{{\Gamma_{s} }}^{ - } } \right)\;{\text{at}}\;\Gamma s$$

where “ + ” and “−” are, respectively, for the plus and minus sides of the corresponding coordinates defining the interface.

Fig. 2

A point-contact lubrication problem. a 3D view b top view of the simulation region with lubrication–contact interfaces

2.2 Flow Conditions

The lubrication–contact interfaces should permit no physical flows to pass through the interface, although the two interactive surfaces are under relative motion. In other words, there is no net flow entering into the solid-contact zones, nor net flow coming out from these zones. For better understanding, dimensional quantities are used in this part. The 2D case only has the Poiseuille and the Couette flows in the X direction, and this zero net flow constraint is expressed as

$$q({x}_{\Gamma }^{-})\equiv {\left.-\frac{{h}^{3}}{12\eta }\frac{d{p}_{\text{f}}}{dx}+\frac{uh}{2}\right|}_{{x}_{\Gamma }^{-}}=0$$

(3)

where h, u, and $\eta$ are the film thickness (or gap), the entrainment velocity, and the viscosity, respectively. In fact, due to flow continuity, zero net flow is true everywhere, and

$$\frac{d{p}_{\text{f}}}{dx}=\frac{6u\eta }{{h}^{2}}$$

(3a)

If the gap is continuous around the interfaces of $h\left({x}_{\Gamma }\right)=0$, $h({x}_{\Gamma }^{-})$ can be infinitely small, thus the pressure gradient in Eq. (3a) can be infinitely large. However, in reality, surface deformation caused by pressures should be included in h, and the 3D lubrication–contact interface allows side flows around the interface. Therefore, the pressure gradient at the interface should be finite. Furthermore, there are other phenomena at the lubrication–contact interface, such as transport of surface adsorbed layers and wall slip, which are not considered in this paper.

The entrainment velocity direction in 3D problems can be arbitrary, and in addition to the motion in the x direction, v is the velocity component along the y direction. The 3D LCICs for zero flows into and out of the solid-contact zones can be expressed in the following four scenarios:

$$q\left( {x_{{\Gamma_{w} }}^{ - } ,y_{{\Gamma_{w} }} } \right) \equiv \left. {\left( { - \frac{{h^{3} }}{12\eta }\frac{{dp_{\text{f}} }}{dx} + \frac{uh}{2}} \right)} \right|_{{x_{{\Gamma_{w} }}^{ - } ,y_{{\Gamma_{w} }} }} = 0\;{\text{at}}\;\Gamma w$$

(4)

$$q\left( {x_{{\Gamma_{e} }}^{ + } ,y_{{\Gamma_{e} }} } \right) \equiv \left. {\left( { - \frac{{h^{3} }}{12\eta }\frac{{dp_{\text{f}} }}{dx} + \frac{uh}{2}} \right)} \right|_{{x_{{\Gamma_{e} }}^{ + } ,y_{{\Gamma_{e} }} }} = 0\;{\text{at}}\;\Gamma e$$

$$q\left( {x_{{\Gamma_{n} }} ,y_{{\Gamma_{n} }}^{ + } } \right) \equiv \left. {\left( { - \frac{{h^{3} }}{12\eta }\frac{{dp_{\text{f}} }}{dy} + \frac{vh}{2}} \right)} \right|_{{x_{{\Gamma_{n} }} ,y_{{\Gamma_{n} }}^{ + } }} = 0\;{\text{at}}\;\Gamma n$$

$$q\left( {x_{{\Gamma_{s} }} ,y_{{\Gamma_{s} }}^{ - } } \right) \equiv \left. {\left( { - \frac{{h^{3} }}{12\eta }\frac{{dp_{\text{f}} }}{dy} + \frac{vh}{2}} \right)} \right|_{{x_{{\Gamma_{s} }} ,y_{{\Gamma_{s} }}^{ - } }} = 0\;{\text{at}}\;\Gamma s$$

In the remaining part of this work, v is assumed to be zero for simplicity. Note that one can apply similar treatments for issues related to u, to be described in the following sections, to handle those related to v if it is not zero.

3 Numerical Implementation

In this section, the LCICs, proposed above, for lubrication problems involving solid contacts are implemented in a discrete format so that they can be incorporated into a numerical algorithm.

3.1 2D Problems

The numerical implementations for the 2D line-contact problem are discussed first, mainly for the purpose of explanation due to its relative simplicity. With both x and h normalized by the Hertzian contact width, a, the dimensionless Reynolds equation can be expressed as

$$\frac{d}{dX}\left(\varepsilon \frac{d{P}_{\text{f}}}{dX}\right)=\frac{d({\rho }^{*}H)}{dX}$$

(5)

with $\varepsilon =\frac{{ap}_{h}}{12u{\eta }_{0}}\frac{{\rho }^{*}{H}^{3}}{{\eta }^{*}}$ and ${P}_{\text{f}}{=p}_{\text{f}}/{p}_{h}$, where ${\eta }_{0}$ is the viscosity at the atmospheric pressure, and ${p}_{h}$ is the maximum Hertzian pressure; X, H, ${\rho }^{*}$, and ${\eta }^{*}$ are dimensionless variables for the coordinate, gap, density, and viscosity defined in the nomenclature. The dimensionless flow can be written as

$$\text{Q}\equiv \frac{qR}{{\rho }_{0}u{a}^{2}}={\rho }^{*}H-\varepsilon \frac{d{P}_{\text{f}}}{dX},$$

(6)

where R is the equivalent radius of the two bodies, and ${\rho }_{0}$ is the density at the atmospheric pressure. Q has the Couette flow

$${\text{Q}}^{C}={\rho }^{*}H$$

(6a)

and the Poiseuille flow

$${\text{Q}}^{P}=-\varepsilon \frac{d{P}_{\text{f}}}{dX}.$$

(6b)

For the derivative of the Poiseuille flow, which is the left-hand side (LHS) term of the Reynolds equation, the second-order central differential scheme is usually applied,

$$\frac{{\varepsilon }_{i-0.5}{P}_{\text{f} i-1}-({\varepsilon }_{i-0.5}+{\varepsilon }_{i+0.5}){P}_{\text{f} i}+{\varepsilon }_{i+0.5}{P}_{\text{f} i+1}}{\Delta {X}^{2}},$$

(7)

where ${\varepsilon }_{i-0.5}=({\varepsilon }_{i-1}+{\varepsilon }_{i})/2$ and ${\varepsilon }_{i+0.5}=({\varepsilon }_{i+1}+{\varepsilon }_{i})/2$ and subscripts $i-0.5$ and $i+0.5$ are middle locations. For the derivative of the Couette flow, which is the right-hand side (RHS) of the Reynolds equation, one can choose from three basic differential schemes: the 1st-order backward (1B), 2nd-order central (2C), or 2nd-order backward (2B) [25, 27, 35, 38]:

(a) 1B scheme:

$$\frac{{\rho }_{i}^{*}{H}_{i}-{\rho }_{i-1}^{*}{H}_{i-1}}{\Delta X}$$

(8)

(b) 2B scheme:

$$\frac{3{\rho }_{i}^{*}{H}_{i}-4{\rho }_{i-1}^{*}{H}_{i-1}+{\rho }_{i-2}^{*}{H}_{i-2}}{2\Delta X}$$

(9)

(c) 2C scheme:

$$\frac{{\rho }_{i+1}^{*}{H}_{i+1}-{\rho }_{i-1}^{*}{H}_{i-1}}{2\Delta X}$$

(10)

Moreover, the derivative of the Couette flow can also be expressed in a separate form [27, 38, 39],

$$\frac{d({\rho }^{*}H)}{dX}={\rho }^{*}\frac{dH}{dX}+H\frac{d{\rho }^{*}}{dX},$$

(11)

which can be discretized with the following options (“S” in the notation stands for “separate”):

• i. S1B scheme: If the 1B scheme is used for the derivatives and ${\rho }^{*}$ and $H$ take values at i,

  $$\begin{gathered} H_{i} \frac{{\rho_{i}^{*} - \rho_{i - 1}^{*} }}{\Delta X} + \rho_{i}^{*} \frac{{H_{i} - H_{i - 1} }}{\Delta X} = \frac{{\rho_{i}^{*} H_{i} - \rho_{i - 1}^{*} H_{i - 1} }}{\Delta X} \hfill \\ + \frac{{\left( {\rho_{i}^{*} - \rho_{i - 1}^{*} } \right)\left( {H_{i} - H_{i - 1} } \right)}}{\Delta X} \end{gathered}$$

  (12)

  which has one more term than what is in Eq. (8). This scheme is used in Eq. (11) of [39].

• ii. If the 1B scheme is used for the derivatives but ${\rho }^{*}$ and $H$ take average values between i and i − 1, one obtains the same equation as Eq. (8).

• iii. S2C scheme: If the 2C scheme is used for the derivatives and ${\rho }^{*}$ and $H$ take values at i,

  $$H_{i} \frac{{\rho_{i + 1}^{*} - \rho_{i - 1}^{*} }}{2\Delta X} + \rho_{i}^{*} \frac{{H_{i + 1} - H_{i - 1} }}{2\Delta X} = \frac{{\rho_{i + 1}^{*} H_{i + 1} - \rho_{i - 1}^{*} H_{i - 1} }}{2\Delta X} + \frac{{\left( {\rho_{i}^{*} - \rho_{i - 1}^{*} } \right)\left( {H_{i} - H_{i - 1} } \right)}}{2\Delta X} - \frac{{\left( {\rho_{i + 1}^{*} - \rho_{i}^{*} } \right)\left( {H_{i + 1} - H_{i} } \right)}}{2\Delta X}$$

  (13)

  which has two more terms than what is in Eq. (10).

• iv. If the 2C scheme is used for the derivatives with ${\rho }^{*}$ and $H$ taking the averages values between i + 1 and i − 1, one obtains the same equation as Eq. (10).

  $$\begin{aligned} \frac{{H_{i + 1} + H_{i - 1} }}{2}\frac{{\rho_{i + 1}^{*} - \rho_{i - 1}^{*} }}{2\Delta X} + \frac{{\rho_{i + 1}^{*} + \rho_{i - 1}^{*} }}{2}\frac{{H_{i + 1} - H_{i - 1} }}{2\Delta X} \\ & = \frac{{\rho_{i + 1}^{*} H_{i + 1} + \rho_{i + 1}^{*} H_{i - 1} - \rho_{i - 1}^{*} H_{i + 1} - \rho_{i - 1}^{*} H_{i - 1} }}{4\Delta X} \\ & + \frac{{ \rho_{i + 1}^{*} H_{i + 1} + \rho_{i - 1}^{*} H_{i + 1} - \rho_{i + 1}^{*} H_{i - 1} - \rho_{i - 1}^{*} H_{i - 1} }}{4\Delta X}\\ & = \frac{{\rho_{i + 1}^{*} H_{i + 1} - \rho_{i - 1}^{*} H_{i - 1} }}{2\Delta X} \\ \end{aligned}$$

  (14)

• v. Using the 2B scheme for the derivatives with ${\rho }^{*}$ and $H$ taking averages values between i + 1 and i − 1 (marked in bold below), one obtains

  $$\frac{{H}_{i+1}+{H}_{i-1}}{2}\frac{3{\rho }_{i}^{*}-4{\rho }_{i-1}^{*}+{\rho }_{i-2}^{*}}{2\Delta X}+\frac{{\rho }_{i+1}^{*}+{\rho }_{i-1}^{*}}{2}\frac{3{H}_{i}-4{H}_{i-1}+{H}_{i-2}}{2\Delta X}$$

• vi. Using the 2B scheme for the derivatives with ${\rho }^{*}$ and $H$ take values at i (marked in bold below), one has

  $${H}_{i}\frac{3{\rho }_{i}^{*}-4{\rho }_{i-1}^{*}+{\rho }_{i-2}^{*}}{2\Delta X}+{\rho }_{i}^{*}\frac{3{H}_{i}-4{H}_{i-1}+{H}_{i-2}}{2\Delta X}$$

Liu et al. [35] presented a flow-continuity view of the discrete Reynolds equation, which is extended in this work to handle the LCICs. Regardless of which differential scheme is used for the derivative of the Couette flow, the discrete Reynolds equation can be expressed in four flow terms as follows:

$${\text{Q}}_{i-0.5}^{P}+{\text{Q}}_{i-0.5}^{C}={\text{Q}}_{i+0.5}^{P}+{\text{Q}}_{i+0.5}^{C},$$

(15)

where the two terms of the flow leaving the node of i are

$${\text{Q}}_{i+0.5}^{P}=-\frac{{\varepsilon }_{i+0.5}({P}_{f,i+1}-{P}_{f,i})}{\Delta X}$$

(16)

$${\text{Q}}_{i + 0.5}^{{\text{C}}} \equiv \left\{ \begin{gathered} \begin{array}{*{20}c} {\rho_{i}^{*} H_{i} ,} & \quad {1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{3\rho_{i}^{*} H_{i} - \rho_{i - 1}^{*} H_{i - 1} }}{2},} & \quad {2{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\rho_{i}^{*} H_{i} + \rho_{i + 1}^{*} H_{i + 1} }}{2},} & \quad {2{\text{C}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\rho_{i}^{*} H_{i} + \left( {{\varvec{\rho}}_{{\varvec{i}}}^{\user2{*}} - {\varvec{\rho}}_{{{\varvec{i}} - 1}}^{\user2{*}} } \right)H_{i} ,} & \quad {{\text{S}}1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\rho_{i}^{*} H_{i} + \rho_{i + 1}^{*} H_{i + 1} }}{2} - \frac{{\left( {\rho_{i + 1}^{*} - \rho_{i}^{*} } \right)\left( {H_{i + 1} - H_{i} } \right)}}{2},} & {{\text{S2C}}} \\ \end{array} \hfill \\ \end{gathered} \right.$$

(17)

and the two terms of the flow entering the node of i, ${\text{Q}}_{i-0.5}^{P}$ and ${\text{Q}}_{i-0.5}^{C}$ are obtained by replacing i with i − 1 in Eqs. (16) and (17), except for the subscripts of ${\rho }_{i}^{*}-{\rho }_{i-1}^{*}$ in S1B, marked in bold in Eq. (17). For example,

$${\text{Q}}_{i - 0.5}^{C} \equiv \left\{ \begin{gathered} \begin{array}{*{20}c} {\rho_{i - 1}^{*} H_{i - 1} ,} & \quad {1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{3\rho_{i - 1}^{*} H_{i - 1} - \rho_{i - 2}^{*} H_{i - 2} }}{2},} & \quad {{\text{2B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\rho_{i}^{*} H_{i} + \rho_{i - 1}^{*} H_{i - 1} }}{2},} & \quad {2{\text{C}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\rho_{i - 1}^{*} H_{i - 1} + \left( {{\varvec{\rho}}_{{\varvec{i}}}^{\user2{*}} - {\varvec{\rho}}_{{{\varvec{i}} - 1}}^{\user2{*}} } \right)H_{i - 1} ,} & \quad {{\text{S}}1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{\rho_{i}^{*} H_{i} + \rho_{i - 1}^{*} H_{i - 1} }}{2} - \frac{{\left( {\rho_{i}^{*} - \rho_{i - 1}^{*} } \right)\left( {H_{i} - H_{i - 1} } \right)}}{2},} & {{\text{S}}2{\text{C}}} \\ \end{array} \hfill \\ \end{gathered} \right.$$

(18)

Furthermore, for the S1B scheme, one could use ${\rho }_{i}^{*}{H}_{i}+{\rho }_{i}^{*}({H}_{i}-{H}_{i-1})$ in Eq. (17) and ${\rho }_{i-1}^{*}{H}_{i-1}+{\rho }_{i-1}^{*}({H}_{i}-{H}_{i-1})$ in Eq. (18). Unlike the equations for options (i)–(iv), those for options (v) and (vi) cannot be further simplified, and if chosen, they should be treated as two terms with the 2B schemes.

Note that for the Couette flow Q^c shown in Eqs. (17–18), the 2C and S2C schemes of Eq. (17) involve subscripts i and i + 1 on the RHS, and the subscript $i+0.5$ on the LHS for ${\text{Q}}_{i+0.5}^{C}$ is their center. Similarly, the 2C and S2C schemes of Eq. (18) contain subscripts i and i $-$ 1 on the RHS, and the subscript $i-0.5$ on the LHS for ${\text{Q}}_{i-0.5}^{C}$ is also their center. However, for the other schemes, subscripts of terms on the RHS, except those of the bold font, are smaller than the subscripts on the LHS. For example, the 1B scheme of Eq. (17) involves subscript i on the RHS, which is smaller than subscript $i+0.5$ on the LHS. Therefore, because the subscript values increase from the left to the right in the discretization (Fig. 3), differential schemes 1B, 2B, or S1B use slightly upstream Couette flow values to approximate the Couette flow terms needed for the element. In Fig. 3, the thick line on the horizontal axis represents one element and these Couette flow terms are illustrated with hollow arrows.

Fig. 3

Lubrication–contact interface in a 2D case, filled circles: lubrication; empty circles: solid contact, with p_f and p_d for the fluid and solid-contact pressures, respectively. The pressure is discretized at nodal points with integer subscripts, but flows are defined at various locations depending on differential schemes. The black arrows show the Poiseuille flows discretized right at i + 0.5 and i-0.5 middle nodes, while the hollow arrows illustrate the Couette flows given by Eqs. (17–18)

The discrete 2D lubrication problem involving a solid-contact zone is shown in Fig. 3. Each node represents a length that connects its two adjacent middle locations. One element is this length shown by the thick line in Fig. 3. The Couette flow terms are illustrated with hollow arrows, and the Poiseuille flows with solid arrows. Note that if the interface location, X_Γ, is known, one could arrange two nodes with X_Γ right at the center. However, X_Γ could be unknown at the beginning of the simulation and change during iterations. In a discrete mesh, if X_Γ is located between two neighboring nodes, the center between these two nodes is used to approximate X_Γ. Of course, a smaller interval between nodes of finer meshes could reduce the error of such an approximation. A dashed line is used in Fig. 3 to represent the geometry at the tip of this solid-contact wedge. i_Γ is used to represent the fluid lubrication node closest to the discrete interface.

In the following, the no-flow constraint is integrated into the discrete Reynolds equation in order to determine the pressure at i_Γ. If film thickness ${H}_{i+1}$ is the first zero value tracing from the inlet from left to right, the interface is between node $i$ and node $i+1$. The middle location, i + 0.5, is chosen to be the interface, so that the no-flow interface condition at this location is ${\text{Q}}_{i+0.5}^{P}+{\text{Q}}_{i+0.5}^{C}=0$, reducing Eq. (15) to,

$${\text{Q}}_{i-0.5}^{P}+{\text{Q}}_{i-0.5}^{C}=0$$

(19)

Therefore, based on the differential schemes for the Couette flow, the following can be obtained:

$$1{\text{B}}:\quad P_{\text{f} i} = P_{\text{f} i - 1} + \frac{{\rho_{i - 1}^{*} H_{i - 1} \Delta X}}{{\varepsilon_{i - 0.5} }}$$

(20)

$$2{\text{B}}:\quad P_{\text{f} i} = P_{\text{f} i - 1} + \frac{{\left( {3\rho_{i - 1}^{*} H_{i - 1} - \rho_{i - 2}^{*} H_{i - 2} } \right)\Delta X}}{{2\varepsilon_{i - 0.5} }}$$

(21)

$$2{\text{C:}}\quad P_{\text{f} i} = P_{\text{f} i - 1} + \frac{{\left( {\rho_{i}^{*} H_{i} + \rho_{i - 1}^{*} H_{i - 1} } \right)\Delta X}}{{2\varepsilon_{i - 0.5} }}$$

(22)

$${\text{S}}1{\text{B}}:\quad P_{\text{f} i} = P_{\text{f} i - 1} + \frac{{\rho_{i}^{*} H_{i - 1} \Delta X}}{{\varepsilon_{i - 0.5} }}$$

(23)

$${\text{S}}2{\text{C:}}\quad P_{\text{f} i} = P_{\text{f} i - 1} + \frac{{\left( {\rho_{i}^{*} H_{i - 1} + \rho_{i - 1}^{*} H_{i} } \right)\Delta X}}{{2\varepsilon_{i - 0.5} }}$$

(24)

Since the net flow is zero everywhere, these recursion formulae are also valid for other nodes in the lubrication zone. Once the fluid and solid-contact pressures are solved, the following inequality needs to be true,

$${P}_{\text{f} {i}_{\Gamma }}\le {P}_{\text{d} {i}_{\Gamma }+1}.$$

(25)

Otherwise, the location of the interface has to be adjusted.

3.2 3D Problems

For 3D problems, the X axis is set along the direction of motion for convenience. Figure 4 shows a simple discrete mixed lubrication scenario. Once a node is found in solid contact, the material of the rectangle element around this node is in solid contact, and, likewise, for the nodes in fluid lubrication the surrounding rectangle is in a state of fluid lubrication. The dashed-line rectangle around node (i, j) is an elemental control volume, and the solid black-line box is the lubrication–contact interface which connects the middle points between fluid and solid-contact nodes.

Fig. 4

a 3D lubrication–contact interface, filled circles: lubrication nodes; empty circles: solid contact nodes. A fluid case and four interface cases are illustrated, on the east, west, south, and north sides of the solid-contact zone marked by the black-line box. b flow terms by various schemes, with black arrows for the Poiseuille flows and hollow arrows for the Couette flow by the 1B, S1B, and 2B schemes. In b, red outlines are used to pair the Couette and the Poiseuille flows on the east borders of the control volumes

3.2.1 Nodes in the Normal Lubrication Zone

If x and h are normalized by the Hertzian contact semi-axis in the x direction, a, and y is normalized by the Hertzian contact semi-axis in the y direction, b, the 2D dimensionless Reynolds equation can be expressed as

$$\frac{\partial }{\partial X}\left(\varepsilon \frac{\partial {P}_{\text{f}}}{\partial X}\right)+\frac{\partial }{\partial Y}\left({k}_{e}^{2}\varepsilon \frac{\partial {P}_{\text{f}}}{\partial Y}\right)=\frac{\partial ({\rho }^{*}H)}{\partial X}$$

(26)

with $\varepsilon =\frac{a{p}_{h}}{12u{\eta }_{0}}\frac{{\rho }^{*}{H}^{3}}{{\eta }^{*}}$ and ${k}_{e}=a/b$, and the dimensionless flows in the X and Y directions can be written as

$${\text{Q}}_{X}\equiv \frac{{q}_{X}}{{\rho }_{0}ua}={\rho }^{*}H-\varepsilon \frac{\partial {P}_{\text{f}}}{\partial X}={\text{Q}}_{X}^{C}+{\text{Q}}_{X}^{P}$$

(27)

$${\text{Q}}_{Y}\equiv \frac{{q}_{Y}}{{\rho }_{0}ua}=-{k}_{e}\varepsilon \frac{\partial {P}_{\text{f}}}{\partial Y}={\text{Q}}_{Y}^{P}.$$

(28)

Descriptions of the differential and finite-difference schemes in 2D problems can be expanded. If node (i, j) and its surrounding four nodes are all under fluid lubrication (Fig. 4, top-right), the discrete Reynolds equation for such a node has a standard form. Equation (7) is extended accordingly with subscript j to represent the derivative of the Poiseuille flow in the X direction in a 3D problem,

$$\frac{{\varepsilon }_{i-0.5,j}{P}_{\text{f} i-1,j}-({\varepsilon }_{i-0.5,j}+{\varepsilon }_{i+0.5,j}){P}_{\text{f} i,j}+{\varepsilon }_{i+0.5,j}{P}_{\text{f} i+1,j}}{\Delta {X}^{2}}$$

(29a)

and the derivative of the Poiseuille flow in the Y direction has a similar expression,

$${k}_{e}^{2}\frac{{\varepsilon }_{i,j-0.5}{P}_{\text{f} i,j-1}-\left({\varepsilon }_{i,j-0.5}+{\varepsilon }_{i,j+0.5}\right){P}_{\text{f} i,j}+{\varepsilon }_{i,j+0.5}{P}_{\text{f} i,j+1}}{\Delta {Y}^{2}},$$

(29b)

where ${P}_{\text{f} i,j}$ is the fluid pressure at the node of (i, j). Five nodes are involved in these discrete equations. The Poiseuille flows in both directions can be expressed as

$${\text{Q}}_{Xi-0.5,j}^{P}=-\frac{{\varepsilon }_{i-0.5,j}({P}_{\text{f}i,j}-{P}_{\text{f}i-1,j})}{\Delta X}$$

(30)

$${\text{Q}}_{Yi,j-0.5}^{P}=-{k}_{e}\frac{{\varepsilon }_{i,j-0.5}({P}_{\text{f}i,j}-{P}_{\text{f}i,j-1})}{\Delta Y}$$

The various differential schemes for the Couette flow in Eqs. (8–14) can be readily applied here by adding the subscript j. Similar to Eqs. (17–18), the following definitions of the Couette flow can be made:

• (a) Couette flow leaving the control volume

  $${\text{Q}}_{X i + 0.5,j}^{C} \equiv \left\{ \begin{gathered} \begin{array}{*{20}l} {\rho_{i,j}^{*} H_{i,j} ,} & \quad {1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{{3\rho_{i,j}^{*} H_{i,j} - \rho_{i - 1,j}^{*} H_{i - 1,j} }}{2},} & \quad {2{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {\frac{{\rho_{i,j}^{*} H_{i,j} + \rho_{i + 1,j}^{*} H_{i + 1,j} }}{2},} & \quad {2{\text{C}}} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {\rho_{i,j}^{*} H_{i,j} + \left( {{\varvec{\rho}}_{{{\varvec{i}},{\varvec{j}}}}^{\user2{*}} - {\varvec{\rho}}_{{{\varvec{i}} - 1,{\varvec{j}}}}^{\user2{*}} } \right)H_{i,j} ,} & \quad {{\text{S}}1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {\frac{{\rho_{i,j}^{*} H_{i,j} + \rho_{i + 1,j}^{*} H_{i + 1,j} }}{2} - \frac{{\left( {\rho_{i + 1,j}^{*} - \rho_{i,j}^{*} } \right)\left( {H_{i + 1,j} - H_{i,j} } \right)}}{2},} & {{\text{S}}2{\text{C}}} \\ \end{array} \hfill \\ \end{gathered} \right.$$

  (31)

• (b) Couette flow entering the control volume

  $${\text{Q}}_{X i - 0.5,j}^{C} \equiv \left\{ \begin{gathered} \begin{array}{*{20}l} {\rho_{i - 1,j}^{*} H_{i - 1,j} ,} & \quad {1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {\frac{{3\rho_{i - 1,j}^{*} H_{i - 1,j} - \rho_{i - 2,j}^{*} H_{i - 2,j} }}{2},} & \quad {2{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {\frac{{\rho_{i,j}^{*} H_{i,j} + \rho_{i - 1,j}^{*} H_{i - 1,j} }}{2},} & \quad {2{\text{C}}} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {\rho_{i - 1,j}^{*} H_{i - 1,j} + \left( {{\varvec{\rho}}_{{{\varvec{i}},{\varvec{j}}}}^{\user2{*}} - {\varvec{\rho}}_{{{\varvec{i}} - 1,{\varvec{j}}}}^{\user2{*}} } \right)H_{i - 1,j} }, & {{\text{S}}1{\text{B}}} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {\frac{{\rho_{i,j}^{*} H_{i,j} + \rho_{i - 1,j}^{*} H_{i - 1,j} }}{2} - \frac{{\left( {\rho_{i,j}^{*} - \rho_{i - 1,j}^{*} } \right)\left( {H_{i,j} - H_{i - 1,j} } \right)}}{2}}, & {{\text{S}}2C} \\ \end{array} \hfill \\ \end{gathered} \right.$$

  (32)

  For the S1B scheme, one can also use ${\rho }_{i,j}^{*}{H}_{i,j}+{\rho }_{i,j}^{*}({H}_{i,j}-{H}_{i-1,j})$ in Eq. (31) and ${\rho }_{i-1,j}^{*}{H}_{i-1,j}+{\rho }_{i-1,j}^{*}({H}_{i,j}-{H}_{i-1,j})$ in Eq. (32).

Elastic deformation is a significant varying portion of ${H}_{i,j}$ in an EHL problem. During iterations, negative values of ${H}_{i,j}$ can occur, indicating potential solid-contact nodes. In most works, negative ${H}_{i,j}$ were set equal to a small value or zero, even at the end of the simulation, leading to erroneous flows/results. Furthermore, one should be aware that such an enforcement is lost during the evaluation of the Poiseuille/Couette flow terms if ${H}_{i,j}$ is separated into terms, or the unenforced version of ${H}_{i,j}$ with negative values is used. In this work, the discrete Reynolds equation is not used for nodes with negative ${H}_{i,j}$, but a new method in Sect. 3.2.7 is applied to determine the solid-contact pressure.

Note that subscripts of the terms on the RHS of Eqs. (31, 32) for the 1B, 2B, and S1B schemes are also slightly shifted from the subscript of Q^c (see Fig. 4b). In other words, the terms on the RHS of the expressions in Eq. (31) are as follows:

• (i) independent of node (i + 1, j) when the 1B, 2B, or S1B scheme is selected. When node (i + 1, j) is in solid contact, these expressions indicate non-zero values of the Couette flow leaving the control volume. As a result, the same amounts of the Couette flow erroneously enter into the neighboring control volume with the solid-contact node. This issue is often overlooked in the literature about mixed lubrication.

• (ii) related to node (i + 1, j) when the 2C or S2C scheme is used. It should be noted that the conventional 2C scheme uses ${\text{Q}}_{X i+0.5,j}^{C}-{\text{Q}}_{X i-0.5,j}^{C}=({\rho }_{i+1,j}^{*}{H}_{i+1,j}-{\rho }_{i-1,j}^{*}{H}_{i-1,j})/2$ without distinguishing which part is entering/leaving the control volume. When node (i + 1, j) is in solid contact and ${H}_{i+1,j}=0$ is enforced, this expression gives

  $${\text{Q}}_{X i+0.5,j}^{C}-{\text{Q}}_{X i-0.5,j}^{C}=-{\rho }_{i-1,j}^{*}{H}_{i-1,j}/2;$$

while with the LCICs enforced in Eq. (31), the net Couette flow in the X direction is

$${\text{Q}}_{X i+0.5,j}^{C}-{\text{Q}}_{X i-0.5,j}^{C}=-({\rho }_{i,j}^{*}{H}_{i,j}+{\rho }_{i-1,j}^{*}{H}_{i-1,j})/2.$$

On the other hand, for the terms on the RHS of Eq. (32), if node (i-1, j) is in solid contact and ${H}_{i-1,j}=0$ is properly enforced,

• (i) the 1B/S1B scheme can effectively turn off the Couette flow entering the control volume since ${H}_{i-1,j}$ is zero.

• (ii) the 2B scheme has node (i − 2, j) involved, and if this node is in lubrication, the Couette flow entering the control volume cannot be effectively turned off; otherwise, this 2B scheme can automatically zero the Couette flow entering the control volume.

• (iii) If the 2C scheme is used, similarly to case (ii) above, the conventional expression gives

  $${\text{Q}}_{X i + 0.5,j}^{C} - {\text{Q}}_{X i - 0.5,j}^{C} = \rho_{i + 1,j}^{*} H_{i + 1,j} /2;$$

while with the LCICs enforced in Eq. (32), the net Couette flow in the X direction is

$${\text{Q}}_{X i + 0.5,j}^{C} - {\text{Q}}_{X i - 0.5,j}^{C} = \left( {\rho_{i,j}^{*} H_{i,j} + \rho_{i + 1,j}^{*} H_{i + 1,j} } \right)/2.$$

Therefore, Eqs. (17–18, 31–32) are critical to the discrete Reynolds equation for lubrication problems involving solid contacts, because they properly identify the Couette flow terms entering and leaving the control volume, thus enabling appropriate treatments of the Couette flow around the lubrication–contact interface.

The discrete Reynolds equation can be expressed in the form of flow continuity as follows:

$${\text{Q}}_{X i-0.5,j}^{P}+{\text{Q}}_{X i-0.5,j}^{C}+\kappa {k}_{e}{\text{Q}}_{Y i,j-0.5}^{P}={\text{Q}}_{X i+0.5,j}^{P}+{\text{Q}}_{X i+0.5,j}^{C}+\kappa {k}_{e}{\text{Q}}_{Y i,j+0.5}^{P},$$

(33)

where $\kappa =\Delta X/\Delta Y.$ After combining the Poiseuille and the Couette flow, the above can be concisely written with four flows as

$${\text{Q}}_{X i-0.5,j}+\kappa {k}_{e}{\text{Q}}_{Y i,j-0.5}={\text{Q}}_{X i+0.5,j}+\kappa {{k}_{e}\text{Q}}_{Y i,j+0.5}.$$

(34)

When one or more of these four surrounding nodes is in solid contact, these equations should be adjusted one by one according to the LCICs mentioned in Sect. 2. In the following subsections, different cases are discussed in detail.

3.2.2 Control Volume with One Border at The Interface

Figure 4 depicts four cases with nodes whose control volumes have one of the four borders at the interface in the 3D problem. For simplicity, each representative node is labeled as (i, j). No flow should penetrate these interface, so that the corresponding flow related to that border of such a control volume should be eliminated in the discrete Reynolds equation, which is detailed as follows:

• (1) West: ${\text{Q}}_{X i+0.5,j}=0$

• (2) East: ${\text{Q}}_{X i-0.5,j}=0$

• (3) North: ${\text{Q}}_{Y i,j-0.5}=0$

• (4) South: ${\text{Q}}_{Y i,j+0.5}=0$

3.2.3 Control Volume with Its Two Connecting Borders at the Interface

Figure 5 shows four cases where the control volumes have their two connecting borders at the interface. No flow penetrates these borders. Each of these cases is a combination of two cases in Sect. 3.2.2. According to their orientations, these cases are labeled as northwest, northeast, southwest, southeast, as shown below:

• (5) Northwest: combination of the north and west cases.

  ${\text{Q}}_{X i+0.5,j}=0$ and ${\text{Q}}_{Y i,j-0.5}=0$

• (6) Northeast: combination of the north and east cases.

  ${\text{Q}}_{X i-0.5,j}=0$ and ${\text{Q}}_{Y i,j-0.5}=0$

• (7) Southwest: combination of the south and west cases.

  ${\text{Q}}_{X i+0.5,j}=0$ and ${\text{Q}}_{Y i,j+0.5}=0$

• (8) Southeast: combination of the south and east cases.

  ${\text{Q}}_{X i-0.5,j}=0$ and ${\text{Q}}_{Y i,j+0.5}=0$

Fig. 5

3D cases with two borders of the control volumes at the interface. Filled circles: lubrication; empty circles: solid contact

3.2.4 Control Volume with Two Parallel Borders at the Interface

Figure 5 also shows two cases where the control volumes have two parallel borders at the interface(s). Similarly, no flow should penetrate these borders. Each of these cases is also a combination of two cases in Sect. 3.2.2. According to their orientations, these cases are labeled as the horizontal and the vertical channels.

• (9) Horizontal channel: ${\text{Q}}_{Y i,j-0.5}=0$ and ${\text{Q}}_{Y i,j+0.5}=0$

• (10) Vertical channel: ${\text{Q}}_{X i-0.5,j}=0$ and ${\text{Q}}_{X i+0.5,j}=0$.

3.2.5 Control Volume with Three Borders at the Interface

The control volume may have three borders at the interface. No flow should penetrate these borders, and as a result, no flow can go through the free border either. These cases are combinations of three cases from the four in Sect. 3.2.2. According to their orientations, these cases are labeled as west open, north open, east open, and south open. If a control volume has only the following border open to the flow (which is, of course, also zero),

• (11) West open: ${\text{Q}}_{X i+0.5,j}=0$, ${\text{Q}}_{Y i,j-0.5}=0$ , and ${\text{Q}}_{Y i,j+0.5}=0$

• (12) East open: ${\text{Q}}_{X i-0.5,j}=0$, ${\text{Q}}_{Y i,j-0.5}=0$ , and ${\text{Q}}_{Y i,j+0.5}=0$

• (13) North open: ${P}_{\text{f} i,j+1}={P}_{\text{f} i,j}$ due to zero Poiseuille flow in the Y direction.

• (14) South open: Similarly, ${P}_{\text{f} i,j-1}={P}_{\text{f} i,j}$

However, nodes inside control volumes of case 10, 13, and 14, where both west and east borders are at the interface, should be processed as solid-contact nodes. Numerical experiments in Sect. 4.4 reveal that this can avoid numerical issues.

Note that Deolalikar et al. [23] treated ${\text{Q}}_{Xi-0.5,j}=0$ occurring in cases (2, 6, 8, 10, 12) with their Eqs. (19–20); however, no treatments are mentioned for other cases listed above. Furthermore, Ref. [23] Eq. (20) may have a typo, i.e., ${B}_{s}$ should be $-\lambda {\overline{\rho }}_{i,j}^{t}{H}_{i,j}^{t}/\Delta X$, and thus it offsets one term of the Couette flow inside Ref. [23] Eq. (19), which utilized the 1B differential scheme for the Couette flow.

In summary, various flow conditions, detailed in Sects. 3.2.2–3.2.5, have been derived to satisfy the LCICs and the discrete Reynolds equation. These conditions are applied in the following section to obtain numerical solutions.

3.2.6 Simplified Treatments

Sections 3.2.2–3.2.5 describe the 2D Reynolds equations modified by the LCICs, when at least one of the discretized nodes is in solid contact. There are fourteen cases in total. One could directly code them into a computer program. Alternatively, one may handle them in simplified ways. The discrete Reynolds equation is written as

$$\begin{gathered} - \frac{{\varepsilon_{i - 0.5,j} \left( {P_{\text{f} i,j} - P_{\text{f}i - 1,j} } \right)}}{\Delta X} + \frac{{\varepsilon_{i + 0.5,j} \left( {P_{\text{f} i + 1,j} - P_{\text{f} i,j} } \right)}}{\Delta X} \hfill \\ - \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} \left( {P_{\text{f} i,j} - P_{\text{f} i,j - 1} } \right)}}{\Delta Y} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j + 0.5} \left( {P_{\text{f} i,j + 1} - P_{\text{f} i,j} } \right)}}{\Delta Y} \hfill \\ = {\text{Q}}_{X i + 0.5,j}^{C} - {\text{Q}}_{X i - 0.5,j}^{C} \hfill \\, \end{gathered}$$

(35)

where the definitions of the Couette flow terms, ${\text{Q}}_{X i+0.5,j}^{C}$ and ${\text{Q}}_{X i-0.5,j}^{C}$, are given in Eqs. (31–32). ${P}_{\text{f} i,j}$ is used for fluid and ${P}_{\text{d} i,j}$ for solid-contact pressures.

In a point-by-point pressure evaluation process, if all four surrounding nodes are in lubrication, no treatment is needed and

$$P_{\text{f} i,j} = {{\left[ {{\text{Q}}_{X i - 0.5,j}^{C} - {\text{Q}}_{X i + 0.5,j}^{C} + \frac{{\varepsilon_{i - 0.5,j} P_{\text{f} i - 1,j} + \varepsilon_{i + 0.5,j} P_{\text{f} i + 1,j} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} P_{\text{f} i,j - 1} + \varepsilon_{i,j + 0.5} P_{\text{f} i,j + 1} }}{\Delta Y}} \right]} \mathord{\left/ {\vphantom {{\left[ {{\text{Q}}_{X i - 0.5,j}^{C} - {\text{Q}}_{X i + 0.5,j}^{C} + \frac{{\varepsilon_{i - 0.5,j} P_{\text{f} i - 1,j} + \varepsilon_{i + 0.5,j} P_{\text{f} i + 1,j} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} P_{\text{f} i,j - 1} + \varepsilon_{i,j + 0.5} P_{\text{f} i,j + 1} }}{\Delta Y}} \right]} {\left[ {\frac{{\varepsilon_{i - 0.5,j} + \varepsilon_{i + 0.5,j} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} + \varepsilon_{i,j + 0.5} }}{\Delta Y}} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\frac{{\varepsilon_{i - 0.5,j} + \varepsilon_{i + 0.5,j} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} + \varepsilon_{i,j + 0.5} }}{\Delta Y}} \right]}}$$

(36)

One could re-arrange the terms in the Couette flow related to ${P}_{\text{f} i,j}$, and increase the denominator of Eq. (36) thus making the iteration process more stable [25, 36]. Otherwise, if any one of the surrounding nodes is in a solid-contact zone (non-positive gap), Eq. (35) needs to be modified to nullify the Poiseuille flow in that direction as follows:

• Method A: the value of $\varepsilon$ is directly adjusted. For example, if node (i-1, j) is under a solid contact, ${\varepsilon }_{i-0.5,j}=0$;

• Method B: the pressure variable(s) at those surrounding nodes are set to be the central pressure value at the last iteration. For example, if node (i-1, j) is under a solid contact, ${P}_{\text{f} i-1,j}$ equals the value of P_{f i,j} at the last iteration.

Furthermore, the Couette flow terms in Eq. (35) have to be adjusted: if one of surrounding solid-contact nodes is on the west side, ${\text{Q}}_{X i-0.5,j}^{C}$ is set to zero, or if one of surrounding solid-contact nodes is on the east side, ${\text{Q}}_{X i+0.5,j}^{C}$ is set to zero. After these necessary treatments, Eq. (36) can then be used to obtain the updated pressure at the current node of the control volume.

If a line-by-line pressure evaluation is executed, one can use this format [27, 36]

$$\alpha_{i} P_{\text{f}i - 1,j} + \beta_{i} P_{\text{f}i,j} + \gamma_{i}^{{}} P_{\text{f}i + 1,j} - \varphi_{i} = 0,$$

(37)

where α_i, β_i, γ_i, and ${\varphi }_{i}$ are coefficients, to be modified accordingly when one or more surrounding nodes are in a solid-contact zone to ensure both the Poiseuille and Couette flow terms are properly removed.

When a single array of ${P}_{i,j}$ is used for both fluid and solid-contact pressures and a point-by-point pressure evaluation process is executed, one may need to define four temporary variables P_e, P_s, P_w, P_n to replace ${P}_{\text{f}, \dots ,j}$ in Eqs. (35–36). Thus,

$$P_{i,j} = {{\left[ {{\text{Q}}_{Xi - 0.5,j}^{C} - {\text{Q}}_{Xi + 0.5,j}^{C} + \frac{{\varepsilon_{i - 0.5,j} P_{w} + \varepsilon_{i + 0.5,j} P_{e} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} P_{s} + \varepsilon_{i,j + 0.5} P_{n} }}{\Delta Y}} \right]} \mathord{\left/ {\vphantom {{\left[ {{\text{Q}}_{Xi - 0.5,j}^{C} - {\text{Q}}_{Xi + 0.5,j}^{C} + \frac{{\varepsilon_{i - 0.5,j} P_{w} + \varepsilon_{i + 0.5,j} P_{e} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} P_{s} + \varepsilon_{i,j + 0.5} P_{n} }}{\Delta Y}} \right]} {\left[ {\frac{{\varepsilon_{i - 0.5,j} + \varepsilon_{i + 0.5,j} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} + \varepsilon_{i,j + 0.5} }}{\Delta Y}} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\frac{{\varepsilon_{i - 0.5,j} + \varepsilon_{i + 0.5,j} }}{\Delta X} + \kappa k_{e}^{2} \frac{{\varepsilon_{i,j - 0.5} + \varepsilon_{i,j + 0.5} }}{\Delta Y}} \right]}}$$

(38)

3.2.7 Solid-Contact Pressure Evaluation and Constraints

Gap values are utilized to determine whether a node is under fluid-film lubrication or solid contact, e.g., a node is marked under solid contact whenever the gap there is below a value corresponding to several layers of adsorbed lubricant molecules [29], or a threshold of 10 nm as selected by Deolalikar et al. [23]. There are different methods to evaluate solid-contact pressures in an EHL problem, among them are (1) the unified Reynolds equation [15]; (2) minimization of complementary energy [14, 23]; and (3) direct pressure determination from the zero gap condition with elastic deformations expressed in terms of pressure estimations (old and new), presented by Zhang and Zhang [24], i.e., based on their Eq. (11), if ${H}_{i,j}^{\text{old}}$ ≤ 0,

$$H_{i,j}^{\text{old}} - D_{0,0} P_{i,j}^{\text{old}} + D_{0,0} P_{i,j}^{\text{new}} = 0,$$

(39)

where ${D}_{\text{0,0}}$ is a pressure-deformation coefficient or an influence coefficient, and P is the solid-contact pressure in this section.

Wang and Zhu [27] mentioned that “to further guarantee the solution convergence and stability, we can introduce a computational control parameter φ whose value is chosen usually between 1 and 2, in order to enhance the leading diagonal elements of the coefficient matrix” of Eq. (37). Zhang and Zhang [24] utilized a similar parameter, but called it a “stability factor” and allowed its value to be 10 to 30. Using C_c for this parameter, Eq. (39) becomes

$${C}_{c}{D}_{\text{0,0}}{P}_{i,j}^{\text{new}}=-{H}_{i,j}^{\text{old}}+{C}_{c}{D}_{\text{0,0}}{P}_{i,j}^{\text{old}}$$

(40)

and ${P}_{i,j}^{\text{new}}$ can be evaluated. Note that the negative values of the gap during iterations provide essential information to determine new estimations of pressure.

In the following, a new method is proposed involving pressures at multiple neighboring nodes:

• (a) If a line-by-line relaxation is used, a new equation for the solid-contact node is constructed following the 3-node iteration format similar to Eq. (37)

  $$D_{1,0} P_{i - 1,j}^{\text{new}} + C_{c} D_{0,0} P_{i,j}^{\text{new}} + D_{1,0} P_{i + 1,j}^{\text{new}} = - H_{i,j}^{\text{old}} + D_{1,0} P_{i - 1,j}^{\text{old}} + C_{c} D_{0,0} P_{i,j}^{\text{old}} + D_{1,0} P_{i + 1,j}^{\text{old}},$$

  (41)

where ${D}_{\text{1,0}}$ is another pressure-deformation/influence coefficient. This equation is suitable for a Jacobi relaxation. When a Gauss–Seidel relaxation is applied, one can bring new pressure values, obtained before relaxing the pressure value for the current node, into Eq. (41). One simple option is to bring in the three values at (i-1, j-1), (i, j-1), and (i + 1, j-1), i.e.,

$$D_{1,0} P_{i - 1,j}^{\text{new}} + C_{c} D_{0,0} P_{i,j}^{\text{new}} + D_{1,0} P_{i + 1,j}^{\text{new}} = - H_{i,j}^{\text{old}} + D_{1,0} P_{i - 1,j}^{\text{old}} + C_{c} D_{0,0} P_{i,j}^{\text{old}} + D_{1,0} P_{i + 1,j}^{\text{old}} + D_{0,1} (P_{i,j - 1}^{\text{old}} - P_{i,j - 1}^{\text{new}} ) + D_{1,1} (P_{i - 1,j - 1}^{\text{old}} - P_{i - 1,j - 1}^{\text{new}} + P_{i + 1,j - 1}^{\text{old}} - P_{i + 1,j - 1}^{\text{new}} ),$$

(41a)

where ${D}_{\text{0,1}}$ is also a pressure-deformation/influence coefficient.

(b) If a pointwise relaxation is adopted, the new equation for the solid-contact node can be expressed as

$$P_{i,j}^{\text{new}} = {{\left[ { - H_{i,j}^{\text{old}} + C_{c} D_{0,0} P_{i,j}^{\text{old}} + D_{1,0} \left( {P_{i - 1,j}^{\text{old}} - P_{i - 1,j}^{\text{new}} } \right) + D_{0,1} (P_{i,j - 1}^{\text{old}} - P_{i,j - 1}^{\text{new}} ) + D_{1,1} \left( {P_{i - 1,j - 1}^{\text{old}} - P_{i - 1,j - 1}^{\text{new}} + P_{i + 1,j - 1}^{\text{old}} - P_{i + 1,j - 1}^{\text{new}} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ { - H_{i,j}^{\text{old}} + C_{c} D_{0,0} P_{i,j}^{\text{old}} + D_{1,0} \left( {P_{i - 1,j}^{\text{old}} - P_{i - 1,j}^{\text{new}} } \right) + D_{0,1} (P_{i,j - 1}^{\text{old}} - P_{i,j - 1}^{\text{new}} ) + D_{1,1} \left( {P_{i - 1,j - 1}^{\text{old}} - P_{i - 1,j - 1}^{\text{new}} + P_{i + 1,j - 1}^{\text{old}} - P_{i + 1,j - 1}^{\text{new}} } \right)} \right]} {\left( {C_{c} D_{0,0} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {C_{c} D_{0,0} } \right)}}.$$

(42)

Involving the neighboring nodes in this method is expected to make the relaxation of the solid-pressure values more stable.

During iteration, a node can change its status between film lubrication and solid contact. If a node in solid contact has one, two, three, or even four surrounding nodes in lubrication (Figs. 4 and 5, where various cases are illustrated), its solid-contact pressure value should be higher than or equal to these fluid pressure values. At the end of the iteration process, these pressure constraints in Eq. (2) have to be satisfied.

4 Numerical Results and Discussion

In the next two subsections, 3D steady-state lubrication problems with simple configurations are used to explain the numerical implementation and validate the proposed LCICs, in terms of flow constraints without evaluating solid-contact pressures. In Sect. 4.3, a steady-state point-contact EHL problem with smooth surfaces is simulated with this new methodology involving the LCICs and the new method to determine solid-contact pressure.

4.1 A Fixed Wedge Bearing Problem

A fixed wedge bearing with a rigid pillar is shown in Fig. 6. It is assumed that (a) the bottom plate is flat and moving along the X axis with a constant velocity of u, and the top pad is stationary; (b) no cavitation around the rigid block; (c) no leakage occurs between the rigid block and the moving plate; and (d) no wall slip is present between lubricant and the plate/pad surfaces. Lubricant density ρ and viscosity η are constant and the solid bodies are rigid in this example. The lubrication zone is governed by a 2D Reynolds equation

Fig. 6

Rigid blockage inside a fixed wedge bearing, and the contact is between the rigid pillar and the moving bottom surface. Four sides of the square are the interfaces

$$\frac{\partial }{\partial X}\left(\frac{{h}^{3}}{\eta }\frac{\partial p}{\partial X}\right)+\frac{\partial }{\partial Y}\left(\frac{{h}^{3}}{\eta }\frac{\partial p}{\partial Y}\right)=-6u\frac{\partial h}{\partial X},$$

(43)

where $h=mX$, and m is the slope of the inclined pad. Coordinates of X and Y are dimensionless with 1 mm as the reference for non-dimensionalization. A dimensionless pressure is defined as

$$P=\frac{{m}^{2}p}{\eta u},$$

(44)

which makes Eq. (43) independent of m. Because with coarser meshes, the central film thickness from the 1B scheme is closer to mesh-convergent results than those from the other schemes in the mixed lubrication simulation based on results presented in [38], the 1B scheme is adopted in this Section. Note that Deolalikar [24] utilized the 1B scheme as well, but other differential schemes can also be selected. With a mesh of 128 by 128 nodes (n = 128), the nodal coordinates are

$$\Delta X = \frac{l}{n - 1.5},\quad X_{i} = X_{0} + \frac{{l\left( {2i - 3} \right)}}{2n - 3},\quad \Delta {\text{Y}} = \frac{b}{n - 1},\quad Y_{i} = - \frac{b}{2} + \frac{{b\left( {i - 1} \right)}}{n - 1}.$$

The first node is deliberately located outside of the plate so that the middle point between the first and second nodes in the X direction is at the edge of the plate, X₀. The following convergence criterion is applied:

$$\frac{\sum \left|{P}^{\text{new}}-{P}^{\text{old}}\right|}{\sum \left|{P}^{\text{new}}\right|}\le {e}^{P},$$

(45)

and the error of pressure, e^p, is 4E-5.

4.1.1 Blockage with a Rigid Square Pillar

A rigid square pillar with side lengths of 8 mm is centered at (35, 0) inside the fixed wedge bearing whose four borders are at ambient pressure (Fig. 6). This pillar is an approximation of a large piece of debris caught in the bearing. The width and length of the bearing plate are 20 and 30 mm, respectively. The coordinates of X₀ and X₁ are 20 and 50 mm, respectively. All these dimensions are illustrations and can be easily altered. Note that there is no analytical solution for this kind of problems. With LCICs, numerical results of the fluid pressure are shown in Fig. 7. A high-pressure zone is observed on the inlet side of the pillar due to flow blockage.

Fig. 7

Fluid pressures over one half of the plate (due to symmetry) when a square pillar (gray part) is in solid contact with the bottom moving surface of the fixed wedge bearing

4.1.2 Blockage with a Rigid Cylindrical Pillar

This example involves a cylindrical pillar, which has a radius of 4 mm, and its center is at (35, 0). The fluid pressure result is plotted in Fig. 8 with the same color map as in Fig. 7. Again, the high-pressure zone is on the inlet side of the pillar but the pressure magnitude is much lower than that in Fig. 6 due to stronger side flows enabled by the cylindrical shape.

Fig. 8

Fluid pressure resulting from the blockage by a cylindrical pillar. The white line in the contour plot (cylindrical surfaces) indicates the lubrication–contact interface

4.2 Effects of LCICs

The fluid pressures in Figs. 7 and 8 are shown together in Fig. 9 along the centerline at Y = 0. The long dashed line is for the traditional solution to the same wedge-bearing problem without the pillar blockage. The rigid blockages result in much higher pressures between the inlet and the blockage, but much lower pressures between the blockage and the exit. The square pillar builds a higher maximum pressure, right in front of the blockage, than does the cylindrical pillar, as expected. When the exit side is completely blocked, an analytical solution has been derived by Liu [36] and the corresponding values at selected locations labeled by “B-Exit ana.” in the legend are shown in Fig. 9 with filled square marks. Numerical results obtained by the iteration process and labeled by “B-Exit num.” are plotted too, and they match the analytical solution very well. One can see clearly that in the zone close to the inlet, the pressure is greater for the square-pillar blockage, followed by the cylinder-pillar blockage, the exit blockage, and the no blockage from high to low.

Fig. 9

Comparison of the pressures in the Y = 0 cross sections for the square-pillar blockage, cylinder-pillar blockage, exit blockage, and no blockage cases. “B-Exit ana.” and “B-Exit num.” are for the analytical and numerical solutions to the exit blockage case

The comparison in Fig. 10 demonstrates the effects of the treatment of the Couette flow based on the proposed LCICs. The label “NTCF” means “no treatment of the Couette flow” and such simulations nullify the Poiseuille flows following LCICs but do not have any treatments on the Couette flows, in order to mimic existing simulation practices. As expected, these results have much higher pressures close to the exit, indicating some Couette flows are allowed improperly from the solid-contact zone to the lubrication zone (see the arrow) in the 1B scheme. The effect of the extra Couette flows is significant in these examples because the local gap values are large. Also as expected, the pressure profiles around the inlet are very close, because the Couette flows there are automatically switched off by the 1B scheme.

Fig. 10

Comparison of pressures. The “NTCF” with the 1B scheme allows the Couette flow exchange (see arrows) when the fluid lubrication zone is on the left-hand side of the solid-contact zone. a the inlet is in the downstream of the numerical discretization, in which the NTCF 1B scheme results in an extra flow out from the solid-contact zone. b the inlet is in the upstream of the numerical discretization in which the NTCF 1B scheme yields an extra flow into the solid-contact zone

The same conditions are simulated with a different configuration in Fig. 10b, where the bearing is rotated 180 degrees with respect to the vertical axis of the blockage. Therefore, the inlet is on the LHS and velocity is from left to right. In this configuration, the pressure build-up peak in the inlet zone from the “NTCF” of the 1B scheme is much lower because this scheme allows some Couette flows unintentionally from the lubrication zone to the solid-contact zone (see the arrow). In summary, “NTCF” with the 1B scheme in fact allows the Couette flow to cross the lubrication–contact interface in both cases (see arrows) when the fluid lubrication zone is on the LHS of the solid-contact zone in the simulation. A denser mesh with 256 by 256 nodes gives very similar pressure values.

4.3 Implementation to EHL and Discussion

In previous sections, blockages are configured inside the simulation domain to illustrate the effects of the LCICs, where solid-contact zones are specified before simulation, and the minimum gaps at the lubrication–contact interfaces are deliberately set non-zero values. In the situation with EHL, such as a smooth sphere rolling on a smooth half-space surface, will solid contacts occur at a low speed? If so, what additional efforts are necessary for the neighborhood of the lubrication–contact interface and for ensuring grid convergence whose importance has been emphasized in [40].

The smooth-surface EHL problem discussed by Hu and Zhu [16] is investigated in this section. Because both the EHL solution and the unlubricated spherical contact result are well known, details regarding the lubrication–contact interface can be quantitatively explored and discussed. The corresponding parameters listed in [16] are adapted: A load of w = 800 N is applied on a spherical steel ball with R_1x = R_1y = 12.7 mm (changed from 19.05 mm [16]) against a steel disk with R_2x = R_2y = ∞ (effective Young’s modulus is E’ = 219.78 GPa), so that the Hertzian contact radius, a, is 0.4108 mm (a = b) and the maximum Hertzian pressure is 2.2631 GPa. The simulation region is − 1.9 ≤ X ≤ 1.3 and − 1.5 ≤ Y ≤ 1.5. The corresponding dimensionless EHL parameters are G = 4000, W = 1E-5, and varying U.

The governing equations are re-stated below for clarity:

• (i) The Reynolds equation, Eq. (26), is only used in the lubrication zone, and H = 0 in the solid-contact zone. A threshold of H_th is introduced to allow flexibility when judging the zones, and the corresponding discrete equations are Eq. (35) for H_i,j > H_th and Eq. (41) for H_i,j ≤ H_th, respectively. The choice of H_th in this work is 0.02 nm normalized by the Hertzian radius a. In addition, for nodes with H_i,j > H_th, whenever their four neighboring nodes have a non-positive gap, treatments in Sects. 3.2.2, 3.2.3, and 3.2.5 should be applied. Case studies in this section show that numerical results obtained in this way satisfy the pressure inequalities in Eq. (2).

  In this problem, ${k}_{e}=1$ and reduced radii R_x = R_y = 12.7 mm. Although other viscosity models are also applicable, the exponential law [41] is used here for simplicity and in agreement with the published works,

  $${\eta }^{*}\equiv \frac{\eta }{{\eta }_{0}}={e}^{\alpha P{p}_{h}}$$

  (46)

  where η₀=0.096 Pa.s, α =18.2 GPa^-1. The Dowson–Higginson pressure–density relationship is adopted:

$${\rho }^{*}\equiv \frac{\rho }{{\rho }_{0}}=1+\frac{0.6\times {10}^{-9}{p}_{h}P}{1+1.7\times {10}^{-9}{p}_{h}P}$$

(47)

• (ii) Equation of the film thickness in Eq. (26) or the gap in Eqs. (39–42) is expressed as

  $$H\left(X,Y\right)={H}_{0}+{B}_{X}{X}^{2}+{B}_{Y}{Y}^{2}-\delta \left(X,Y\right)+V\left(X,Y\right),$$

  (48)

  where H₀ is the normal approach of two surfaces, varying with the load. ${B}_{X}=a/{R}_{x}/2$ and ${B}_{Y}=a/{R}_{y}/2$. The $\delta$ term is for microscale surface feature, such as roughness, and is zero in this Section.

• (iii) Elastic deformation is written as

  $$V(X,Y) = C_{e} \iint\limits_{\Omega } {\frac{P(\xi ,\zeta )}{{\sqrt {(X - \xi )^{2} + (Y - \zeta )^{2} } }}}{\text{d}}\xi {\text{d}}\zeta$$

  (49)

  with $C_{e} = 2k_{e} p_{h} /(\pi E^{\prime})$. This equation is valid under the half-space assumption and linear elasticity, and one can replace it with other deformation models, such as those for layered materials, inhomogeneous materials, and viscoelastic materials.

• (iv) The load balance equation is

  $$\iint\limits_{\Omega } {P(X,Y)\,}{\text{d}}X{\text{d}}Y = \frac{2\pi }{3}.$$

  (50)

• (v) The conventional boundary conditions for this EHL problem are zero pressure at the four sides of the simulation region and pressure cannot be negative. More details can be found in references [27, 38].

Each integration in Eq. (49) is a convolution, and after discretization, the elastic deformation can be expressed as

$$V_{k,l} = C_{e} \sum\limits_{i} {\sum\limits_{j} {D_{|k - i|,|l - j|}^{{}} p_{i,j} } },$$

(51)

where ${D}_{i,j}$ is the influence coefficients. The discrete convolution-Fast Fourier Transform algorithm [42] can be applied to significantly reduce the computation burden of the double convolutions.

The unified equation system [15, 16, 27, 39] essentially uses the Reynolds equation for the entire simulation region, where negative film thickness was replaced with a fixed small value or zero in the Poiseuille-flow terms. However, the film thickness in the Couette flow and the squeeze term is often substituted with the summation, i.e., the RHS of Eq. (48). Therefore, the derivatives with respect to X and time are applied to each film contributor separately. It should be noted that in this way, if the summation is negative, the Couette flow and the squeeze terms actually use the film contributors whose summation is negative. Although at the end of calculation, the negative film-thickness values can be set to zero or a small value for output, the negative film-thickness values should be minimized as close to zero as possible. This new modeling methodology reported in this work aims to obtain solutions with negligible negative film thickness without artificial enforcement.

One of the purposes of this Section is to observe the lubrication–contact interface at low speeds; therefore, the behavior involving two smooth surfaces in the steady state is calculated. The 1B scheme is used with the Jacobi relaxation. Equation (37) is applied to construct the linear equation in a line-by-line fashion if a nodal gap is positive; otherwise Eq. (41) is used. A stable linear equation is critical for solving the low-speed problem, and dominant diagonal elements, β_i, can improve the stability of convergence. Reference [35] discussed adjustments to these coefficients in the linear equations in detail by collecting certain terms from the elastic deformation contributor in the film thickness, which occurs on the RHS of the Reynolds equation. These coefficients are expressed as follows:

$$\left\{ \begin{gathered} \alpha_{i} = \frac{{\varepsilon_{i - 0.5} }}{{\Delta X^{2} }} - \frac{{\rho_{i,j}^{*} D_{1,0}^{{}} - \rho_{i - 1,j}^{*} D_{0,0}^{{}} }}{\Delta X} \hfill \\ \beta_{i} = - \frac{{\varepsilon_{i - 0.5} + \varepsilon_{i + 0.5} }}{{\Delta X^{2} }} - \frac{{\rho_{i,j}^{*} D_{0,0}^{{}} }}{\Delta X} \hfill \\ \gamma_{i} = \frac{{\varepsilon_{i + 0.5} }}{{\Delta X^{2} }} - \frac{{\rho_{i,j}^{*} D_{1,0}^{{}} - \rho_{i - 1,j}^{*} D_{2,0}^{{}} }}{\Delta X} \hfill \\ \varphi_{i} = \frac{1}{\Delta X}\left[ \begin{gathered} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho_{i,j}^{*} (H_{i,j} - D_{1,0}^{{}} P_{i - 1,j} - D_{0,0}^{{}} P_{i,j} - D_{1,0}^{{}} P_{i + 1,j} ) \hfill \\ - \rho_{i - 1,j}^{*} (H_{i - 1,j} - D_{0,0}^{{}} P_{i - 1,j} - D_{2,0}^{{}} P_{i + 1,j} ) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right.$$

(52)

If ${P}^{\text{new}}$ is the collection of new estimations of pressure with members evaluated from Eq. (37) at positive gaps, or from Eq. (41) otherwise, a relaxation process is applied to obtain P^new by

$$P = P^{\text{old}} - \omega_{p} (P^{\text{new}} - P^{\text{old}} ),$$

(53)

where the relaxation factor ${\omega }_{P}$ can have different values for different nodes, and one can optimize them to reduce iteration steps. In this section, the lubrication nodes have a constant ${\omega }_{P}$ of 0.01 or 0.02, of which one-third is used for the solid-contact nodes. With both lubrication and solid-contact pressure considered, the unbalanced load is used to improve the old estimation of the normal approach in every 2 or 4 iterations of the pressure relaxation.

$$H_{0}^{\text{new}} = H_{0}^{\text{old}} - \omega_{w} (\frac{2\pi }{3} - \Delta X\Delta Y\sum {\sum {P_{i,j} } } )$$

(54)

Thus, the relaxation process only has a single loop. The error of the load

$$\left| {\frac{{2\pi /3 - \Delta X\Delta Y\sum {\sum P } }}{2\pi /3}} \right|$$

(55)

is less than 1E-4, and the desired error of pressure, e^p in Eq. (45) is below 1E-4 or smaller if possible. Iteration details are recorded in Table 1. Quantities of “e^p lubr.” and “e^p solid” are calculated for reference when lubrication pressures and the solid-contact pressures are separately used in the definition of the error of pressure in Eq. (45).

Table 1 Numerical details, G = 4000, W = 1E-5

For bodies with smooth surfaces, only the entrainment velocity (u) matters. This velocity is set at 0.005 mm/s (U = 1.15E-16) for the first simulation, which is between the values (10 and 0.001 mm/s) used in Fig. 1e and f of Hu and Zhu [16]. The number of nodes is 257 by 257 with ΔX = 0.0125 and ΔY = 0.0117188.

Under such a slow motion, solid contact dominates over the Hertzian contact circle with negligible lubrication around it. Figure 11a shows the distributions of pressure along the X and Y axes, which are very close to the theoretical distribution of the Hertzian pressure in the dotted line. The difference between them is plotted in Fig. 11b over the solid-contact zone to show details. Note that the nodes in the range of 73 ≤ i ≤ 233 on the X axis or 44 ≤ j ≤ 214 on the Y axis are in contact, and the pressure deviation from the Hertzian pressure is very small over the Hertzian contact circle, while a few nodes next to the lubrication–contact interface have slightly greater deviations than those inside the contact zone. This can be attributed to the large pressure gradient around the lubrication–contact interface. The pressures in the lubricated zone are plotted in Fig. 11c and d, although they are close to zero. Profiles of film thickness/gap along the X and Y axis are shown in Fig. 11e focusing details inside the Hertzian contact circle. In this solver, no truncation is enforced to the film thickness/gap, but H = 0 is solved for the solid-contact nodes with H_th of 0.02 nm as the threshold of the gap to differentiate solid contact and lubrication. The new method to determine the solid-contact pressure functions well since gaps in the solid-contact zone have negligibly small residual values, even under such a magnification, i.e., H of 1E-9 is 4.7E-4 nm. Overall, results in Fig. 11 show several important features: (1) solid-contact pressures are close to the Hertzian theoretical values; (2) hydrodynamic pressure is built up in front of and around the contact blockage; (3) no hydrodynamic pressure is on the exit side of the contact blockage; (4) negligible gap values truly indicate the status of solid contact; and (5) pressure constraints at the interface are satisfied.

Fig. 11

Results with G = 4000, W = 1E-5, and U = 1.15E-16. The mesh has 257 by 257 nodes. a pressure comparison and b difference between the current calculated pressure and the Hertzian theoretical pressure, c lubrication pressures along the inlet on the negative X axis and the negative Y axis, d lubrication pressure along the outlet on the positive X axis and the positive Y axis, and e detail of the gap in the solid-contact zone. (H of 1E-9 is 4.7E-4 nm)

In order to examine the mesh effect, the number of nodes is increased. The pressure-difference profiles, the zoom-in views of the lubrication pressure, and the film-thickness profiles are plotted in Fig. 12 for the mesh of 513 by 513. Nodes within 145 ≤ i ≤ 465 in the X direction or 87 ≤ j ≤ 427 in the Y direction are in contact, see Fig. 12a. Figure 12a shows smaller deviations from the Hertzian theoretical pressure with a finer mesh. The residual gaps over the contact area in Fig. 12b are extremely small negative values. The five features mentioned above are also true in Fig. 12. Figure 13a shows a comparison of the lubrication pressure along Y = 0 in the upstream of the lubrication–contact interface, with up to 1025 by 1025 nodes. The lubrication pressure build-up is higher for the finer meshes at nodes close to the interface. This behavior agrees with that of a blocked flow anticipated by the continuum fluid mechanics, and under small errors of lubrication pressure,“e^p lubrication” listed in Table 1, lubrication solutions in Fig. 13a–c are reasonably converged and demonstrate grid independency. As one can see, from Fig. 13c, the pressure at the nodes under the solid contact close to the lubrication–contact interface are grid converged as well.

Fig. 12

Pressure differences from the Hertzian pressure, lubrication pressure and film-thickness profiles at Y = 0 and X = 0, respectively. The mesh has 513 by 513 nodes, G = 4000, W = 1E-5, and U = 1.15E-16. a pressure difference between the current and the Hertzian theoretical values, b detail of the gap, or the film thickness (H of 1E-9 is 4.7E-4 nm), c lubrication pressure around the inlet on the negative X axis and on the negative Y axis, and d lubrication pressure around the outlet on the positive X axis and on the positive Y axis

Fig. 13

Comparison of the lubrication pressure build-ups around the lubrication–contact interface. a pressure in a linear axis, b film thickness or gaps, c pressure in a log vertical axis, including one node under solid contact for each mesh

In the following results, 1025 by 1025 nodes are used to explore the transition from full-film lubrication to deep solid contact since numerical results from a coarser mesh may have undulations. If the entrainment speed is 7.5 mm/s (U = 1.72E-13), the central film thickness is around 12.4 nm (14.7 nm from Hamrock and Dowson’s formula) and the minimum film thickness is about 1.0 nm based on this new solver; therefore, from the continuum point of view and for smooth surfaces, a full-lubrication film is established through the entire lubrication junction. With smaller U values around 3.44E-14 (1.5 mm/s), the constrictions on the two sides of the horse-shoe-shaped film thickness start to make solid contacts. When the entrainment speed is further reduced, these solid-contact zones expand toward the center of the contact, as shown in Fig. 14a, where the film-thickness results along the Y direction are plotted. The numerical configurations are summarized in Table 1. Note that some cases with small central film thicknesses have a numerical stability problem although the datum fluctuation is small, which made it difficult to reduce the e^p values. In Fig. 14b, the pressure profiles on the inlet side are shown for the six different speeds. A contour plot of the film thickness/gap is depicted for the case with U values of 2.29E-15 (0.1 mm/s), where the black areas are solid-contact zones.

Fig. 14

Transition from full-film lubrication to full solid contact (inside the Hertzian zone). a Film-thickness profiles along the Y direction with six different velocities, b pressure profiles on the inlet side, c contour view of the film thickness/gap for the case with U = 2.29E-15 (0.1 mm/s)

From the continuum mechanics point of view, Fig. 14, together with the results from the entrainment speed of 7.5 mm/s (U = 1.72E-13) and 0.005 mm/s (U = 1.15E-16), demonstrates the complete lubrication transition from full-film lubrication to full solid contact (inside the Hertzian zone). With the given load, materials, geometry, and lubricant (G = 4000, W = 1.00E-5), two surfaces completely separate from each other at the velocity above 3.44E-14 (1.5 mm/s), and they have the full solid contact inside the Hertzian zone at around 0.01 mm/s (U = 2.29E-16).

5 Conclusions

Lubrication–contact interface conditions (LCICs) between fluid film and solid contact in lubrication problems were investigated. Expressions for the Couette flows entering or leaving a control volume have been mathematically defined for several differential schemes. A set of LCICs, including nullifying flows and pressure inequalities, are presented, and a new method to determine solid-contact pressure is proposed.

Methods for numerical implementation of the LCICs have been developed, and solutions to several problems involving simple geometries have been obtained with the first backward scheme as a test example. The numerical results with the treatment of the Couette flows around the interface clearly capture the effect of a contact blockage, while those without such a treatment can artificially allow flows to enter into or exit the blockage, thus affecting the accuracy of lubrication analyses. The derived LCICs and their corresponding treatments can eliminate the extra-flow problems, thus enabling more precise mixed-EHL simulations.

The LCICs and the related contact and flow treatment methods have been integrated into a new mixed/boundary EHL solver, and a steady-state smooth-body point-contact EHL problem has been solved from deep solid contact to full-film lubrication. The interface between the fluid film and solid contact is captured, and the critical speeds for complete surface separation and complete contact are identified for the material and conditions studied.