Cylinder-Flat Contact Mechanics with Surface Roughness

Abstract

We study the nominal (ensemble averaged) contact pressure p(x) acting on a cylinder squeezed in contact with an elastic half space with random surface roughness. The contact pressure is Hertzian-like for $\alpha < 0.01$ and Gaussian-like for $\alpha > 10$, where the dimensionless parameter $\alpha = h_{\rm rms}/\delta$ is the ratio between the root-mean-square roughness amplitude and the penetration for the smooth surfaces case (Hertz contact).

1 Introduction

The pressure or stress acting in point contacts, e.g., when an elastic ball is squeezed against a nominal flat surface, or in line contacts, e.g., when an elastic cylinder is squeezed against a flat surface, has many important applications, such as the contact of a railway wheel and the rail (point contact) or in O-ring seals (line contact). In many of these applications, the surface roughness has a big influence on the nominal contact pressure profile. In a recent study for metallic (steel) seals, we found that the maximum of the nominal contact pressure was reduced by a factor of $\approx 3$ when the surface roughness was taken into account in the analysis [1]. This has a huge influence on the fluid leakrate and led us to perform a more general study, which we report here, of the influence of the surface roughness on the pressure profile for line contacts.

In a classical study, Greenwood an Tripp [2] (see also Ref. [3]) studied the influence of surface roughness on the elastic contact of rough spheres. They used the Greenwood–Williamson [4] (GW) contact mechanics theory where the elastic coupling between the asperity contact regions is neglected. However, later studies have shown that this coupling is very important even for small nominal contact pressures, where the distance between the macroasperity contact regions may be large [5]. The reason is that there are smaller asperities (microasperities) on top of the big asperities, and since the contact pressure in the macroasperity contact region in general is very high, the microasperity contact regions are closely spaced and the elastic coupling between them cannot be neglected. In the present study, we will use the Persson contact mechanics theory which includes the elastic coupling between all asperity contact regions in an approximate but accurate way [6, 7].

We note that the GW model is approximately valid if roughness occurs on just one length scale [8]. Now, when the applied squeezing force is small, the average surface separation, which determines the influence of the surface roughness on the nominal contact pressure, depends mainly on the most long wavelength roughness component. Thus, for small applied force, the GW theory gives an approximately correct nominal pressure distribution if the asperities in the GW model are chosen as the long wavelength roughness part of the roughness spectrum. However, this approximation breaks down at high enough applied force and cannot describe the area of real contact for any applied force as it depends on the whole roughness spectrum.

Many studies of the contact between rough spheres have been presented [2, 3, 9,10,11,12,13]. Most of them assume only elastic deformations, but a few studies include plastic deformations and adhesion. Most recent studies are based on numerical methods such as the finite element method, the boundary element method, or molecular dynamics. However, numerical methods cannot be easily applied to real surfaces of macroscopic solids, which typically have roughness extending over very many decades in length scales. Here, we will use the Persson contact mechanics theory [6, 15,16,17] to study the influence of surface roughness on the nominal contact pressure for the contact between a cylinder and a flat (line contact, see Fig. 1). For this case, we are only aware of one study of the type presented here, but using the GW theory [18].

Fig. 1

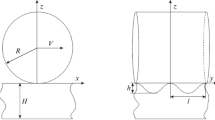
Two limiting cases when a rigid cylinder (black) with radius R is squeezed against a nominal flat half space (green). a If the surface roughness amplitude is very small, or the applied force is very high, the nominal contact area will be determined by bulk deformations and given by the Hertz contact theory. b In the opposite limit, mainly the surface asperities deform (but with a long-range elastic coupling occurring between them). In this limit, the pressure profile is Gaussian-like (Color figure online)

2 Theory

Consider an elastic cylinder squeezed against an elastic half space with the cylinder axis parallel to the surface of the half space (flat). The surfaces of the cylinder and the flat have random roughness with the power spectra $C_1(q)$ and $C_2(q)$, respectively. For stationary elastic contact, we can map the original problem on another simpler problem, where the cylinder is rigid and the half space elastic with the effective Young’s modulus

$$\begin{aligned} {1\over E^*} = {1-\nu _1^2\over E_1} +{1-\nu _2^2\over E_2}. \end{aligned}$$

(1)

Here, $E_1$ and $\nu _1$ are the Young’s modulus and Poisson ratio of the cylinder, and $E_2$ and $\nu _2$ of the half space. The cylinder surface is perfectly smooth, while the flat has the (combined) surface roughness $h=h_1+h_2$. We assume that the surface roughness on the two surfaces are uncorrelated so that the combined surface roughness power spectrum (on the flat)

$$\begin{aligned} C(q)=C_1(q)+C_2(q). \end{aligned}$$

(2)

Here, we have used that $\langle h_1(\mathbf{x}) h_2(\mathbf{x'})\rangle = 0$ (uncorrelated roughness), where $\langle \ldots \rangle$ stands for ensemble averaging.

From the theory of elasticity [19],

$$\begin{aligned} u=u_1+{x^2\over 2R} -{2\over \pi E^*} \int _{-\infty }^\infty {\rm d}x' \ p(x') \left| {x-x'\over x'} \right| , \end{aligned}$$

(3)

where p(x) and u(x) are the contact pressure and the interfacial separation, averaged over different realizations of the surface roughness. In (3), $u_1$ must be chosen so that the applied normal force per unit length $f_{\rm N}$ satisfies

$$\begin{aligned} \int _{-\infty }^\infty {\rm d}x \ p(x) = f_{\rm N}. \end{aligned}$$

(4)

Finally, the Persson contact mechanics theory gives a relation p(u) between the nominal contact pressure and the interfacial separation u, averaged over different realizations of the surface roughness [20]. For the case of not too high or too low contact pressures, where the system either approach complete contact or the contact is so small that only a few asperities makes contact (finite-size region) [14], we have [15]

$$\begin{aligned} p=\beta E^* e^{-u/u_0}, \end{aligned}$$

(5)

where $u_0 = \gamma h_{\rm rms}$ (with $\gamma \approx 0.4$) and $\beta$ are numbers determined by the surface roughness power spectrum.

If we measure the surface displacement u in units of the sphere or cylinder radius R, and the pressure p in units of the effective modulus $E^*$, we get from (3)–(5):

$$\begin{aligned}&p\approx \beta e^{-u R/u_0},\\ & u=u_1+{x^2\over 2} -{2\over \pi } \int {\rm d}x' \ p(x') \left| {x-x'\over x'} \right| . \\&\int _{-\infty }^\infty {\rm d}x \ p(x) = {f_{\rm N} \over RE^*} . \end{aligned}$$

Note that the problem depends on the two dimensionless parameters $u_0/R$ and $f_{\rm N}/(RE^*)$. We find it more useful to use instead of $f_{\rm N}/(RE^*)$ the parameter $[u_0/R][RE^*/f_{\rm N}]= \gamma h_{\rm rms}E^*/f_{\rm N}$. Defining $\delta = [4/\pi ] [f_{\rm N}/E^*]$ the second parameter is essentially $\alpha = h_{\rm rms}/\delta$, where $\delta$ is the penetration for smooth surfaces (see (9) below). The parameter $\alpha$ was already introduced by Greenwood et al. [2, 3] in their study of the influence of roughness on the contact between elastic spheres.

We have solved the equations given above numerically, but two limiting cases can be easily studied analytically, namely, the case of smooth surfaces where the classical Hertz theory is valid, and in the case where the roughness is very big or the applied force is $f_{\rm N}$ small. In the second case, we can neglect the bulk deformations and just include the deformations of the asperities; we refer to this limit as the Gaussian limit.

2.1 Hertzian Limit

For smooth surfaces ($h_{\rm rms}=0$), the contact is Hertz-like with the pressure distribution [19]

$$\begin{aligned} p=p_0 \left( 1-\left( {x\over a}\right) ^2 \right) ^{1/2}, \end{aligned}$$

(6)

where

$$\begin{aligned} p_0= & {} \left( {E^* f_{\rm N} \over \pi R}\right) ^{1/2} \end{aligned}$$

(7)

$$\begin{aligned} a= & {} \left( R\delta \right) ^{1/2} \end{aligned}$$

(8)

$$\begin{aligned} f_{\rm N}= & {} {\pi \over 4} E^* \delta . \end{aligned}$$

(9)

For the Hertz contact pressure (6), the ratio between the full-width-at-half-maximum (FWHM) w and the standard deviation s of p(x) is easy to calculate: $w/s = 2\surd 3 \approx 3.464$.

2.2 Gaussian Limit

When a cylinder with a smooth surface is squeezed against a flat smooth substrate, an infinite long rectangular contact region of width 2a is formed, with the contact pressure given by the Hertz theory (6). However, if the substrate has surface roughness, the nominal contact region will be larger than that predicted by the Hertz theory, and the pressure distribution will change from parabolic-like for the case of smooth surfaces to Gaussian-like if the surface roughness is large enough. This can be easily shown using the Persson contact mechanics theory.

Due to the surface roughness, if the contact pressure p is not too high, the interfacial separation u is related to the contact pressure via (see 5) [20]

$$\begin{aligned} p=\beta E^* e^{-u/u_0}. \end{aligned}$$

(10)

Neglecting bulk deformations, for a cylinder with radius R squeezed against the flat, we expect (see (3) with $E^* \rightarrow \infty$):

$$\begin{aligned} u \approx u_1+{x^2 \over 2R} \end{aligned}$$

(11)

so that

$$\begin{aligned} p=p_0 e^{-x^2/2s^2}. \end{aligned}$$

(12)

where $s^2 = Ru_0 = \gamma R h_{\rm rms}$. Using (12), we get

$$\begin{aligned} \int _{-\infty }^\infty {\rm d}x \ p_0 e^{-x^2/2s^2} = p_0 s ( 2\pi )^{1/2} = f_{\rm N} \end{aligned}$$

or

$$\begin{aligned} p_0 = {f_{\rm N} \over s (2\pi )^{1/2}} \end{aligned}$$

(13)

We note that (12) holds only as long as the pressure p is so small that the asymptotic relation (10) is valid, but not too small as then finite-size effects become important. In addition, in deriving (12), we have neglected bulk deformations. This is a valid approximation only if $s\gg a$ , $h_{\rm rms} \gg \delta$ , or $\alpha = h_{\rm rms}/\delta \gg 1$. In this limit, the maximal contact pressure is much smaller than the result for smooth surfaces given by the Hertz formula (7). Thus, the ratio between (12) and (7) is

$$\begin{aligned} {p_0 ({\rm rough}) \over p_0({\rm smooth})} = \left( {f_{\rm N} \over 2 \gamma E^* h_{\rm rms}}\right) ^{1/2} = \left( {\pi \over 8 \gamma \alpha }\right) ^{1/2}. \end{aligned}$$

(14)

Since $\gamma \approx 0.4$ this ratio is about $0.9 \alpha ^{-1/2}$.

For a Gaussian function, the ratio between the FWHM w and the standard deviation s is easy to calculate: $w/s = 2 (2 {\rm ln} 2)^{1/2} \approx 2.355$

The study above can also be applied to the contact between a sphere and a flat. In that case

$$\begin{aligned} u \approx u_1+{r^2 \over 2R} \end{aligned}$$

giving

$$\begin{aligned} p=p_0 e^{-r^2/2s^2}. \end{aligned}$$

If $F_{\rm N}$ is the applied squeezing force

$$\begin{aligned} \int {\rm d}^2x \ p_0 e^{-r^2/2s^2} = F_{\rm N} \end{aligned}$$

giving

$$\begin{aligned} p_0 = {F_{\rm N} \over 2 \pi s^2}. \end{aligned}$$

Note that the asperities act like a compliant layer on the surface of the body, so that contact is extended over a larger area than it would be if the surfaces were smooth and, in consequence, the contact pressure for a given load will be reduced. In reality, the contact area has a ragged edge which makes its measurement subject to uncertainty. However, the rather arbitrary definition of the contact width is not a problem when calculating physical quantities like the leakage of seals, which can be written as an integral involving the nominal pressure (see Ref. [1, 21]).

Note also the fact that the nominal contact pressure p(x) for $\alpha \gg 1$ is a Gaussian function of x has nothing to do with the fact that randomly rough surfaces has a Gaussian distribution of asperity heights. Rather, it results from the fact that there is an exponential relation between the contact pressure and average interfacial separation (see (5)), and the fact that when bulk deformations can be neglected (which is the case for $\alpha \gg 1$), the average interfacial separation depends quadratically on the lateral coordinate x as long as $x/R \ll 1$ (see (11)).

2.3 Role of Plastic Deformation

The derivation of the nominal contact pressure profile presented above assumes elastic deformations. If the stress at the onset of plastic flow is higher than the maximum stress $p_0$, and the maximal shear stress, at the surface, and also below the surface in the cylinder-flat contact region, then no macroscopic plastic deformation will occur. In that case, for smooth surfaces, we expect no macroscopic plastic deformations and can treat the contact as elastic when calculating the nominal contact pressure distribution. However, the stress in the asperity contact regions is much higher than the nominal contact pressure. Thus, assuming elastic contact, the relative contact area [7, 8] $A/A_0 \approx (2/h') (p_0/E^*)$, where $h'$ is the rms slope. Since the average pressure p in the asperity contact regions must satisfy $p A = p_0 A_0$ , we get $p=(A_0/A) p_0\approx h'E^*/2$. Thus, at short enough length scale (where $h'$ is large enough), we expect plastic deformations to occur in many cases. However, the indentation hardness of many solids increases as the size of the indentation decreases, and if this effect is large enough no plastic deformation may occur on any length scale [22].

Even when plastic deformation occur, (12) may still be approximately valid if the asperities deform elastically on the length scale which determines the contact stiffness for the (nominal) contact pressures relevant for the calculation of (12). The contact stiffness (or the p(u) relation) for small pressures is determined by the most long wavelength roughness components which may deform mainly elastically. Nevertheless, in general, a detailed study is necessary in order to determine the exact influence of plastic flow at the asperity level on the nominal contact pressure profile.

Fig. 2

The surface roughness power spectra C(q) as a function of the wavenumber q (log–log scale) for three different surfaces, 1–3, with the root-mean-square (rms) roughness amplitude and the Hurst exponents ($h_{\rm rms}=10 \ {\upmu }m$, $H=0.8$) (surface 1, red curve) ($10 \ {\upmu }m$, 1.0) (surface 2, green curve), and ($1 \ {\upmu }m$, 0.8) (surface 3, blue curve) (Color figure online)

Fig. 3

The contact pressure p(x) as a function of the coordinate x for a rigid cylinder squeezed against an elastic half space. The red line is for a perfectly smooth surface (Hertz contact), and the black line is for surface 1 with the surface roughness power spectrum given by the red line in Fig. 2. The pink line is obtained using (12), i.e., neglecting the elastic deformations of the bulk. The loading force $f_{\rm N} = 10 \ {\rm kN/m}$ (Color figure online)

Fig. 4

The ratio w/s between the full-width-at-half-maximum (FWHM) w and the standard deviation s as a function of the logarithm of the dimensionless number $\alpha = h_{\rm rms}/\delta$, where $h_{\rm rms}$ is the rms surface roughness amplitude and $\delta = 4f_{\rm N}/(\pi E^*)$ is the penetration in the Hertz theory (smooth surfaces). In the calculation, we have used the power spectra in Fig. 2, and only varied the loading force $f_{\rm N}$ (between $1000 \ {\rm N/m}$ and $1.5\times 10^6 \ {\rm N/m}$). The cylinder radius $R=1 \ {\rm cm}$ and the effective modulus $E^*=1.33 \ {\rm GPa}$ (Color figure online)

Fig. 5

The ratio $p_0({\rm rough})/p_0({\rm smooth})$ between the maximum of the contact pressure for rough and smooth surfaces, as a function of the logarithm of the dimensionless number $\alpha = h_{\rm rms}/\delta$. The dashed line is the large $\alpha$ asymtotic result (14). The green and blue lines are for surface 2 and 3, respectively, with the surface roughness power spectra given in Fig. 2. As for the ratio w/s, the surface 1 gives the same result as surface 2 and is not shown. In the calculation, we have used the power spectra in Fig. 2 and only varied the loading force $f_{\rm N}$ (between $1000 \ {\rm N/m}$ and $1.5\times 10^6 \ {\rm N/m}$). The cylinder radius $R=1 \ {\rm cm}$ and the effective modulus $E^*=1.33 \ {\rm GPa}$ (Color figure online)

Fig. 6

A sandblasted (6 bar air pressure for 5 minutes) aluminum surface indented by a steel ball (radius $R=2 \ {\rm cm}$) with $500 \ {\rm N}$ force. Top: The plastically flattened asperities reflect the light giving the white domains within a circle with the diameter $\approx 1.5 \ {\rm mm}$, which is larger than the diameter of the contact area obtained from the Hertz theory for smooth surfaces (about $0.9 \ {\rm mm}$). Bottom: stylus line scan through the middle of the indented surface area (Color figure online)

3 Numerical Results and Discussion

We will now present numerical results to illustrate the influence of surface roughness on the nominal contact pressure profile. In the calculation, we will use three surfaces, 1–3, with the roughness power spectra shown in Fig. 2. The surface 1 has the root-mean-square (rms) roughness amplitude $10 \ {\upmu } m$, and the Hurst exponent $H=0.8$. The other two surfaces have $h_{\rm rms}=10 \ {\upmu } m$ , $H=1.0$ (surface 2, green line), $h_{\rm rms}=1 \ {\upmu } m$ , and $H=0.8$ (surface 3, blue line). Note that we include one decade roll-off region, from $q=10^3 \ {\rm m}^{-1}$ to $q=10^4 \ {\rm m}^{-1}$. We assume the effective Young’s modulus $E^*=1.33 \ {\rm GPa}$ and the radius of the cylinder $R=1 \ {\rm cm}$. We vary the applied pressure $f_{\rm N}$ from $10^3\ {\rm N/m}$ to $1.5\times 10^6 \ {\rm N/m}$. This gives a variation in $\alpha = h_{\rm rms}/\delta$ with more than 3 decades.

Figure 3 shows the contact pressure p(x) as a function of the coordinate x for a rigid cylinder squeezed against an elastic half space with the force $f_{\rm N} = 10 \ {\rm kN/m}$. The red line is for a perfectly smooth surface (Hertz contact), and the black line for the surface 1 with the surface roughness power spectrum is given in Fig. 2 (red line). The pink line is obtained using (12), i.e., neglecting the elastic deformations of the bulk. Note that the surface roughness reduces the maximal contact pressure and makes the pressure profile Gaussian-like, but it becomes a perfect Gaussian only for much larger values of the parameter $\alpha$ (corresponding to smaller applied force $f_{\rm N}$ or larger rms roughness amplitude $h_{\rm rms}$). Note also that including both the deformations of the asperities and the bulk (black curve) gives a wider pressure distribution than assuming that only the asperities deform elastically (pink curve).

Figure 4 shows the ratio w/s between the full-width-at-half-maximum (FWHM) and the standard deviation s as a function of the logarithm of the dimensionless number $\alpha = h_{\rm rms}/\delta = (\pi /4) (h_{\rm rms} E^*/ f_{\rm N})$. In the calculation, we have used the three power spectra shown in Fig. 2 and varied the loading force $f_{\rm N}$ (between $10^3 \ {\rm N/m}$ and $1.5\times 10^6 \ {\rm N/m}$). Note that as a function of $\alpha$ , the ratio w/s is nearly the same for all three surfaces and that the contact pressure is Hertzian-like for $\alpha < 0.01$ and Gaussian-like for $\alpha > 10$. This study suggests that the nominal pressure distribution p(x) depends mainly on the parameter $\alpha$, as already suggested by Greenwood et al. [3].

Figure 5 shows the ratio $p_0({\rm rough})/p_0({\rm smooth})$ between the maximum of the contact pressure for the rough and the smooth surfaces, as a function of the logarithm of the dimensionless number $\alpha$. We show results for the surfaces 2 and 3 (surface 1 gives nearly the same result as surface 2). The dashed line is the large $\alpha$ asymtotic result (14), and for $\alpha > 10$ , it gives nearly identical result as obtained for surfaces 1–3.

In this study, we have neglected plastic deformation. Plastic deformation may be very important for metals, in particular during the first contact [23, 24]. As an example, in Fig. 6 (top), we show the plastically deformed area of a sandblasted aluminum surface after squeezing (normal force $F_{\rm N} = 500 \ {\rm N}$) a steel sphere (radius $R=2 \ {\rm cm}$) with very smooth surface, against the aluminum surface. Note that asperities have been smoothed by plastic flow and act as small mirrors resulting in the white regions in the optical picture (observed in reflected light). In this case, some bulk plastic flow has also occurred, as is clear from the topography line scan in Fig. 6 (bottom), but similar experiments on a steel surface exhibit only plastic deformations of asperities.

Note that the contact region is not compact. The diameter of the circular region including all the plastically deformed asperities is $\approx 1.5 \ {\rm mm}$, which is larger than the calculated Hertz contact region for smooth surfaces (diameter $\approx 0.9 \ {\rm mm}$). In fact, the nominal contact region during the contact with the sphere may be even larger than indicated by Fig. 6 because there may be an annular (elastic contact) region outside the plastically deformed region, where the contact pressure is too low to induce plastic deformations of the aluminum asperities. Similar plastic effects may occur in some cases in the line contact problem studied above.

4 Summary and Conclusion

We have studied the dependency of the nominal contact pressure on the surface roughness and the loading force when a rigid cylinder is squeezed against an elastic half space. We found that the contact pressure is Hertzian-like for $\alpha < 0.01$ and Gaussian-like for $\alpha > 10$, where the dimensionless parameter $\alpha = h_{\rm rms}/\delta$ is the ratio between the root-mean-square roughness amplitude and the penetration for the smooth surfaces case (Hertz contact).