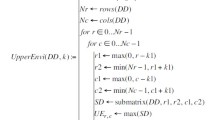Abstract
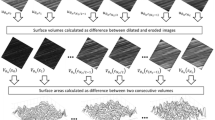
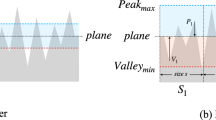
The curvature of surface topography is quantified in this study using a newly developed directional blanket covering curvature (DBCC) method. The novel method addresses a long-standing problem of a measurement of a local surface curvature at individual scales and directions. The curvature data are obtained using the first and second derivations of the quadratic polynomial fitted to the local surface profile extracted from the surface height image data at individual scale and direction. The range of scales is set between an instrument spatial resolution and 1/10 of the image shortest size. Using the surface curvature data, three parameters, i.e. curvature, peak and valley dimensions, are calculated as the slopes of lines fitted to data point subsets of log–log plots of surface areas (differences between dilated and eroded surface curvature matrices) against scales of calculation. The dimensions quantify directional changes in the overall curvature and the curvature of peaks and valleys at individual scales. The scale corresponds to the centre of the subset. A flat surface criterion based on the surface areas was also proposed. Using the criterion, a flat surface was identified in computer images of dome, corrugated plate and fractal surface. The DBCC method was applied to computer-generated fractal surfaces with increasing curvature complexity, sine waves with decreasing curvature at single scale and microscope images of isotropic (sandblasted) and anisotropic (ground) surfaces of titanium plates. Results showed that the method is accurate in the measurement of surface curvature and the detection of minute changes occurring in the curvature of real surfaces over a wide range of scales.






Similar content being viewed by others
Abbreviations
- \(A\) :
-
Surface area
- \(A_{\text{PEAK}} ,A_{\text{VALLEY}}\) :
-
Peak and valley surface areas
- \({\text{abs}}\) :
-
Absolute value function
- \(a_{0} , a_{1} ,a_{2}\) :
-
Coefficients of quadratic function
- \(B_{\varepsilon }\) :
-
Structuring element
- \(b\) :
-
Eroded version of K
- c :
-
Constant
- CD:
-
Curvature dimension
- \({\text{CD}}_{\text{MEAN}}\) :
-
Mean curvature dimension
- \(\text{C}_{\text{Str}}\) :
-
Curvature aspect ratio
- \({\text{FD}}\) :
-
Fractal dimension
- \({\text{FD}}_{\text{t}}\) :
-
Theoretical fractal dimension
- \(f\) :
-
Surface function
- \(f_{\kappa }\) :
-
Curvature function
- \(f_{\text{q}}\) :
-
Quadratic function
- G f :
-
Graph
- I :
-
Image function
- J:
-
Rotated image matrix
- \(L_{x} ,L_{y}\) :
-
Spatial domains
- l :
-
Subset size
- \(l_{x}\) :
-
Line length
- \(l_{y}\) :
-
Distance between peak and line
- \(N_{\varepsilon }\) :
-
Number of scales
- \(N_{\theta }\) :
-
Number of directions
- \(N_{x} ,N_{y}\) :
-
Number of grid points in spatial directions
- \(N_{z}\) :
-
Number of greyscale levels
- \({\text{PD}}\) :
-
Peak dimension
- \({\text{PD}}_{\text{MEAN}}\) :
-
Mean peak dimension
- \(\text{P}_{\text{Str}}\) :
-
Peak aspect ratio
- \(r_{c}\) :
-
Peak radius
- \({\text{Sds}}\) :
-
Density of peaks
- Sku:
-
Kurtosis
- Spc:
-
Arithmetic mean curvature of peaks
- Ssc:
-
Mean curvature of summits
- Sta:
-
Texture major axis
- Str:
-
Texture aspect ratio
- Th:
-
Threshold
- V :
-
Accumulated volume
- VD:
-
Valley dimension
- VDMEAN :
-
Mean valley dimension
- VStr :
-
Valley aspect ratio
- u :
-
Dilated version of K
- X, Y :
-
Spatial domains
- x, y :
-
Spatial coordinates
- z :
-
Surface height
- ε :
-
Scale
- θ :
-
Direction
- K :
-
Surface curvature matrix
- K PEAK :
-
Surface peak matrix
- K VALLEY :
-
Surface valley matrix
- κ :
-
Profile curvature
- \({\text{\copyright}}\) :
-
Curvature operation
References
Whitehouse, D.J.: Handbook of Surface and Nanometrology, 2nd edn. CRC Press, Boca Raton (2010)
Bhushan, B.: Principles and Applications of Tribology, 2nd edn. Wiley, New York (2013)
ASME B46.1: Surface Texture, Surface Roughness. American Society of Mechanical Engineers, New York, Waviness and Lay (2002)
ISO 25178–2: Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms: Definitions and Surface Texture Parameters. International Organization of Standardization, Geneva (2012)
Blunt, L.A., Jiang, X.: Advanced Techniques for Assessment Surface Topography. Kogan Page Science, London (2003)
Calabi, E., Olver, P.J., Shakiban, C., Tannenbaum, A., Hake, S.: Differential and numerically invariant signature curves applied to object recognition. Int. J. Comput. Vision 26, 107–135 (1998)
Vulliez, M., Gleason, M.A., Souto-Lebel, A., Quinsat, Y., Lartigue, C., Kordell, S.P., Lemoine, A.C., Brown, C.A.: Multiscale curvature analysis and correlations with the fatigue limit on steel surfaces after milling. Procedia CIRP. 13, 308–313 (2014)
Gleason, M.A., Morgan, C., Lemoine, A., Brown, C.A.: Multi-scale calculation of curvatures from an aspheric lens profile using Heron’s formula. In: Proceedings of ASPE/ASPEN Summer Topical Meeting, Manufacture and Metrology of Freeform and Off-Axis Aspheric Surfaces, June 26–27, 2014, Hawaii, USA, pp. 98–102 (2014)
Nowicki, B.: Multiparameter representation of surface roughness. Wear 102, 161–176 (1985)
Bigerelle, M., Nianga, J.M., Najjar, D., Iost, A., Hubert, C., Kubiak, K.J.: Roughness signature of tribological contact calculated by a new method of peaks curvature radius estimation on fractal surfaces. Tribol. Int. 65, 235–247 (2013)
Hubert, C., Kubiak, K.J., Bigerelle, M., Dubois, A., Dubar, L.: Identification of lubrication regime on textured surfaces by multi-scale decomposition. Tribol. Int. 82, 375–386 (2015)
Theisel, H., Rossi, C., Zayer, R., Seidel, H.-P.: Normal based estimation of the curvature tensor for triangular meshes. In: PG 2004: Proceedings of 12th Pacific Conference on Computer Graphics and Applications, 6–8 Oct 2004, pp. 288–297 (2004)
Bartkowiak, T., Lehner II, J.T., Hyde, J., Wang, Z., Brown, C.A., Pedersen, D.B., Hansen, H.N.: Multi-scale areal curvature analysis of fused deposition surfaces. In: Proceedings of the 2015 ASPE Spring Topical Meeting: Achieving Precision Tolerances in Additive Manufacturing, ASPE, Raleigh, NC. 60, pp. 77–82 (2015)
Bartkowiak, T., Hyde, J., Brown, C.A.: Multi-scale curvature tensor analysis of surfaces created by micro-EDM and functional correlations with discharge energy. In: 5th International Conference on Surface Metrology, 4th–7th April 2016, Poznan University of Technology, Poland, Conference Proceedings/© Poznan University of Technology (2016)
Bouligand, G.: Sur la notion d’ordre de mesure d’un ensemble ferme´. Bull. Sci. Math. 52, 185–192 (1929)
Mandelbrot, B.B.: The Fractal Geometry of Nature. W.H. Freeman and Company, San Francisco (1982)
Geraets, W.G.M.: Comparison of two methods for measuring orientation. Bone 23, 383–388 (1998)
Stewart, J.: Multivariable Calculus. Brooks/Cole Publishing Company, Pacific Grove (1995)
Peleg, S., Naor, J.: Multiple resolution texture analysis and classification. IEEE Trans. Pattern Anal. Mach. Intell. 6, 518–523 (1984)
Wolski, M., Podsiadlo, P., Stachowiak, G.W.: Applications of the variance orientation transform method to the multiscale characterization of surface roughness and anisotropy. Tribol. Int. 43, 2203–2215 (2010)
Wolski, M., Stachowiak, G.W., Dempsey, A.R., Mills, P.M., Cicuttini, F.M., Wang, Y., Stoffel, K.K., Lloyd, D.G., Podsiadlo, P.: Trabecular bone texture detected by plain radiography and variance orientation transform method is different between knees with and without cartilage defects. J. Orthop. Res. 29, 1161–1167 (2011)
Bryan, J.B.: The Abbe principle revisit: an updated interpretation. Precis. Eng. 1, 129–132 (1979)
Stein, M.L.: Fast and exact simulation of fractional Brownian surfaces. J. Comput. Graph. Stat. 11, 587–599 (2002)
Acknowledgments
The authors wish to thank Curtin University and the Department of Mechanical Engineering for their support during preparation of the manuscript. The study was conducted as part of the Implementing Agreement on Advanced Material for Transportation Applications, Annex IV Integrated Engineered Surface Technology. The Implementing Agreement functions within a framework created by the International Energy Agency (IEA). The views, findings and publications of the AMT IA do not necessarily represent the views or policies of the IEA or of all of its individual member countries.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest for this manuscript.
Rights and permissions
About this article
Cite this article
Podsiadlo, P., Wolski, M. & Stachowiak, G.W. Novel Directional Blanket Covering Method for Surface Curvature Analysis at Different Scales and Directions. Tribol Lett 65, 2 (2017). https://doi.org/10.1007/s11249-016-0786-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11249-016-0786-4