1 Introduction

Identifying the acid and basic strength of surface sites is essential to rationalize the catalytic properties of oxide surfaces. Metal cations are potential electron charge acceptors, i.e. Lewis acids, while O2− anions play the role of conjugated bases [1, 2]. The selectivity of many reactions is influenced not only by the nature of the acidic and basic sites but also by their number and acid/base strength.

Zirconium dioxide (ZrO2) is an important material with acid/base character [3] and is very stable under oxidizing and reducing atmospheres [4]. For this reason, is an interesting catalyst support [5] and a catalyst on its own [6]. Zirconia has at least five stable structural polymorphs [7, 8] with different properties. The monoclinic ZrO2 phase (m-ZrO2) is stable at low temperature [9]. Around 1400 and 2600 K, there is a first- and second-order phase transition to tetragonal [10] and cubic [11] structures, respectively. The most stable facet of tetragonal zirconia (t-ZrO2), (101), is the same as the most stable cubic zirconia (111) surface [12]. The brookite (orthorhombic-I) and cotunnite (orthorhombic-II) phases are high pressure-induced phases of zirconia [7, 13].

We have chosen t-ZrO2 (101) and m-ZrO2 (\(\bar{1}11\)) surfaces for this study since these are the most stable surfaces of the two common phases of zirconia [14]. On the other hand, nanocrystalline materials exhibit unique structural features with distinct properties and catalytic activity [15]. In this work we focus on fully dehydrated models of different zirconia structures. This is because our interest is on the Lewis acidity and basicity of the surface, while the presence of surface OH groups can result also in Broensted acidity.

Carbon monoxide (CO) has been widely studied as a probe molecule to characterize the Lewis acidity of zirconia [16, 17] using infrared (IR) spectroscopy [16, 18]. Other studies, such as temperature-programmed desorption [19], and calorimetry [20], as well as theoretical studies [21, 22] have been reported. The determination of surface basicity is more complex as the probe molecules, such as carbon dioxide (CO2) [23], may dissociate or give rise to complex surface reactions. Adsorption of pyrrole (C4NH5) as a probe molecule to detect the basic sites on the surface of metal oxides and to estimate their basic strength has been studied by IR [24, 25] and nuclear magnetic resonance (NMR) [26,27,28] spectroscopies, and will be considered here from a theoretical point of view.

Studies of the acid–base properties of tetragonal [21, 29] and monoclinic [30] ZrO2 as well as of other metal oxides [31, 32] have been reported already. Structural defects of oxide surfaces such as steps, exhibiting low-coordinated O2− and Mn+ sites, are expected to affect the interaction with adsorbates [33]. However, not always the change in coordination number results in a measurable change in acidity or basicity [21].

In this work we will discuss the acidity and basicity of regular t-ZrO2 (101) and m-ZrO2 (\(\bar{1}11\)) and stepped t-ZrO2 (134) and m-ZrO2 (\(\bar{2}12\)) surfaces, as well as of zirconia nanoparticles of size ranging between 1.5 and 2 nm, (ZrO2±x)n with n = 13–85 [34,35,36,37,38].

2 Methods

The calculations have been performed by means of the VASP 5.4.4 package [39,40,41]. The valence electrons, H (1s), C (2s, 2p), N (2s, 2p), O (2s, 2p) and Zr (4s, 5s, 4p, 4d), are expanded on a set of plane waves with a kinetic cut-off of 400 eV, whereas the core electrons are treated with the Projector Augmented Wave (PAW) approach [42, 43]. The generalized gradient approximation (GGA) for the exchange–correlation functional was applied, with the Perdew−Burke−Ernzerhof (PBE) formulation [44]. The GGA + U approach implemented by Dudarev et al. was used to partly correct the self-interaction error of GGA functionals, that affects the electronic structure [45, 46]. In particular, the onsite Coulomb correction, Ueff = U–J, was set to 4 eV for the 4d states of Zr atoms [34, 47]. The D3 dispersion energy was included by means of the Becke−Johnson damping [48, 49].

The lattice parameters of bulk m- and t-zirconia were fully optimized with a kinetic energy cutoff of 600 eV and an 8 × 8 × 8 Monkhorst−Pack k-point grid; the resulting parameters were fixed in all slab calculations. A slab of four and five ZrO2 layers was used for the (\(\bar{1}11\)) and (101) surfaces. For the (\(\bar{1}11\)) surface, a 2 × 2 supercell (Zr64O128) was used, whereas for the (101) surface, a 3 × 2 supercell with Zr60O120 formula was taken. For the stepped surfaces, on the basis of the previous work [50], we adopted 1 × 1 supercells of t-ZrO2 (134) surface with 3 layers of ZrO2 (Zr24O48). The monoclinic stepped surface (\(\bar{2}12\)) [5, 51] were modeled with a three-layer thick stepped zirconia film with a 2 × 1 unit cell and Zr60O120 formula. For all cases, a vacuum region > 10 Å is present to remove the slab−slab interactions. For zirconia nanostructures, the stoichiometric nanoparticles Zr16O32 and Zr40O80 were considered [34, 35].

For all models, we performed structural relaxations of all atoms with convergence criteria of 10−5 eV and 10−2 eV/Å for the electronic and ionic loops, respectively. The sampling of the reciprocal space is set to the Γ-point for m-ZrO2 (\(\bar{1}11\)) and (\(\bar{2}12\)), t-ZrO2 (101) and zirconia nanoparticles: this choice still ensures reasonable accuracy, given the large size of the adopted supercells. For t-ZrO2 (134) stepped surface, we used 3 × 2 × 1 k-point meshes.

The isotropic chemical shift (δiso) is computed as δiso = σref − σcalc, where σref is the shielding value of the reference and σcalc is the chemical shielding obtained in VASP. For 1H, 15N, and 13C NMR, on the basis of experimental reports, we consider tetramethylsilane (TMS) [52], ammonia (NH3) [53], and TMS [54], respectively, as the references with 31, 255 and 178 ppm chemical shielding calculated by VASP. For 17O NMR, on the basis of previous reports considering that the bulk oxygen anions have more regular arrangements than the oxygen anions at the surface, a constant value can be used to determine the reference chemical shift (δref):

$$\delta_{{{\text{ref}}}} = \delta_{{{\text{iso}}}} \left( {{\text{bulk}}\left( {\exp} \right)} \right) - m\sigma_{{{\text{calc}}}} \left( {{\text{bulk}}\left( {{\text{calc}}} \right)} \right)$$
(1)

here δiso(bulk(exp)) is the experimental chemical shift of bulk m-ZrO2 (325 ppm) [55]. σcalc(bulk(calc)) refers to the chemical shielding of oxygen atoms in inner layers that have constant value (− 344 ppm for regular m-ZrO2 (\(\bar{1}11\)) slab); m is a gradient assumed to be equal − 1 [55]. Thus, δref can be determined as − 17 ppm for m-ZrO2 surfaces. The results of 17O NMR chemical shift (δiso) of the m-ZrO2 surfaces are summarized in the Supporting Information. For t-ZrO2 surfaces and nanoparticles, we employed the same strategy of our previous work to calculate δref which is fixed at − 36 ppm [38]. Since the reference for calculation of the 17O chemical shift of oxygen anions in m- and t-ZrO2 slabs is different, we consider the chemical shielding of water [55], 317 ppm, as the reference for calculation of 17O chemical shift of O atoms in the CO adsorbed molecule.

Vibrational frequencies are calculated within the harmonic approximation via diagonalization of the dynamical matrix. The active fragment for the ionic displacements is restricted to the adsorbed molecules and the surface ions directly taking part in the adsorption process.

Finally, the adsorption energies (EADS) have been calculated according to the following equation:

$${\text{E}}_{{{\text{ADS}}}} = {\text{E}}\left( {{\text{x}}/{\text{ZrO}}_{{2}} } \right) - {\text{E}}\left( {\text{x}} \right)\left( {\text{g}} \right) - {\text{E}}\left( {{\text{ZrO}}_{{2}} } \right)$$
(2)

where x is the adsorbed molecule and ZrO2 the oxide support.

3 Results and Discussions

3.1 Acid Properties: CO Adsorption

In this section, we explore the acidity of Zr atoms in different ZrO2 structures. Changes of stretching frequency and 13C and 17O NMR of adsorbed CO in comparison with the free CO molecule will be discussed.

3.1.1 Regular m-ZrO2 (\(\bar{1}11\)) and t-ZrO2 (101) Surfaces

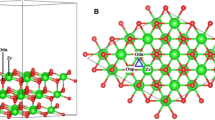
On the m-ZrO2 (\(\bar{1}11\)) surface there are four non-equivalent Zr atoms, Fig. 1. Zr-A, Zr-B, and Zr-C are six-fold coordinated, Zr6c, while Zr-D is seven-fold coordinated, Zr7c. Figure 2a–c shows the CO adsorption on Zr-A to -C, respectively. The properties of CO adsorption on all zirconia surfaces are summarized in Table 1. During the optimization, starting from CO on Zr-D, CO moves to Zr-A. The adsorption energies (EADS) of CO to the Zr atoms are in the range − 0.49 to − 0.56 eV, Table 1. The CO frequencies are blue-shifted with respect to the free CO, from a minimum of + 12 to a maximum of + 29 cm−1. Experimentally, shifts of + 31/ + 51 cm−1 have been reported for CO on m-ZrO2 [56]. The C–O bond length decreases slightly by adsorption on both m- and t-ZrO2 surfaces. The Zr-C bond distances are in the range 2.506–2.576 Å. The bonding of CO to the surface does not imply a charge transfer, as it is shown by the net CO Bader charges that are always smaller than 0.03 |e| in absolute value (see Table S1).

Fig. 1
figure 1

Position of Zr atoms (big blue spheres: A-D) and O atoms (small red spheres: 1–8) on the first layer of the m-ZrO2 (\(\bar{1}11\)) surface. a Side, b Top views

Full size image
Fig. 2
figure 2

Optimal structures of CO on regular, a–d, and stepped, e–h, ZrO2 surfaces. The panels a to c, e and f show the adsorption on m-ZrO2 surfaces and the panels d, g and h the adsorption on t-ZrO2 surfaces. Blue, red and brown spheres are Zr, O and C atoms, respectively

Full size image
Table 1 Adsorption energy (EADS, eV), bond length (R, Å), C–O stretching frequency (ν, cm−1) and 13C chemical shift (δiso, ppm) of CO on ZrO2 surfaces and Zr16O32 and Zr40O80 nanoparticles
Full size table

The results of 13C NMR show that the C atom of adsorbed CO is shielded, and δiso(13C) decreases by about − 9 ppm and goes to higher field. The changes of 17O chemical shift of the O atom of CO are not significant, and will not be further discussed.

On the t-ZrO2 (101) surface there is only one kind of zirconium, the 7-coordinated zirconium cation (Zr7c), Fig. 2d. The interaction of CO with Zr7c has an adsorption energy of − 0.50 eV, close to that computed for Zr6c sites on the m-ZrO2 (\(\bar{1}11\)) surface, see Table 1. The C–O stretching frequency and δiso(13C) are shifted by + 7 cm−1 and − 2 ppm, respectively. The experimental data for changes in C–O stretching frequency on t-ZrO2 surface is reported + 51 cm−1 [18]. The difference with respect to our calculations is due to the fact that higher levels of theory (hybrid functionals) and correction for anharmonic effects need to be included in order to obtain a quantitative estimate of this property. On the other hand, the trend is correct and the CO stretching frequency can be safely used to probe different acid sites on the surface of zirconia.

3.1.2 Stepped m-ZrO2 (\(\bar{2}12\)) and t-ZrO2 (134) Surfaces

In this section we explore the adsorption of CO on low-coordinated Zr sites on stepped m-ZrO2 (\(\bar{2}12\)), Fig. 2e, f, and t-ZrO2 (134), Fig. 2g, surfaces. The maximum and minimum adsorption energies of CO, − 0.61 and − 0.39 eV, are observed for Zr6c and Zr7c on stepped (Fig. 2g) and regular terrace (Fig. 2h) sites of the t-ZrO2 (134) surface, respectively. Also, the shift in stretching frequency of CO on the stepped site of t-ZrO2 (134) is the largest observed + 36 cm−1 (to be compared to a shift of − 4 cm−1 on the flat region of the step). The bond distance of C to Zr is between 2.506 and 2.638 Å.

In Fig. 3 we plot the change in CO stretching frequency versus the adsorption energy, EADS, for all zirconia structures considered.

Fig. 3
figure 3

The plot of EADS against ΔνCO of the CO molecule on the regular and the stepped surfaces (Fig. 2a–h) and nanostructures (Fig. 4c–h) of ZrO2

Full size image

On Table 1 we have reported the 13C chemical shifts (δiso) of adsorbed CO. Upon adsorption, δiso(13C) of CO is shifted to lower ppm (− 1 to − 3 ppm for tetragonal and − 8 to − 10 ppm for monoclinic surfaces) while the changes of 17O NMR of adsorbed CO are not noticeable. These shifts appear too small to provide a measure of the different properties of the various acid sites.

3.1.3 ZrO2 Nanoparticles

Now we consider two zirconia stoichiometric clusters to model the properties of zirconia nanostructures. Details on how these have been obtained and on their electronic structure can be found in refs [34,35,36,37]. We have studied the adsorption of CO on different surface Zr atoms of Zr16O32 (Fig. 4a–d) and Zr40O80 (Fig. 4e–h). The adsorption energy of CO is in the range − 0.50 to − 0.85 eV, i.e. it is a bit stronger than on the regular surface. The CO bond distances, with two exceptions, are slightly shortened with respect to the free molecule (1.144 Å), an effect that results in a positive shift in CO vibrational frequency of + 23 to + 60 cm−1, see Table 1. However, two CO adsorption modes on Zr16O32, Fig. 4a and b, show red-shifts in the C–O stretching frequency by − 53 and − 9 cm−1, respectively. This is a clear indication that some Zr ions on the ZrO2 nanoparticles still have residual electron density to be back-donated to the 2π* MO of the adsorbed CO molecule. For the same reason, also, the changes in δiso(13C) are out of range compared to the other sites (Fig. 4c–h), see Table 1. This shows that some specific Zr sites in the stoichiometric nanoparticles have much weaker acid character than other sites. The bonding of CO to the apical Zr site of Zr16O32, Fig. 4a, shows a CO frequency shift and a NMR signal completely different from the other sites. This is clear manifestation of the fact that we are in a non-scalable regime, where properties change with size but also with the site considered. Here, a partial accumulation of charge on the apical Zr atom results in an enhanced back donation to CO which reinforces the bond with the nanoparticle. The presence of such sites is not observed in zirconia particles of larger size.

Fig. 4
figure 4

Optimal structures of CO on Zr16O32 (a–d) and Zr40O80 (e–h) nanoparticles. The blue, red and brown spheres are Zr, O and C atoms, respectively

Full size image

The changes in δiso(13C) of adsorbed CO on Zr16O32 and Zr40O80 nanoparticles, Fig. 4c–h and Table 1, are in a range from − 5 to − 9 ppm while the changes of 17O NMR are, once more, negligible.

The adsorption energy of the CO molecule on various Zr cations of different surfaces (Fig. 2a–h) and nanostructures (Fig. 4c–h) has been plotted against the CO stretching frequency (Fig. 3). The resulting curve shows some correlation of the two properties (R2 = 0.83), and can be taken as a descriptor of the acid character of the sites. In particular, higher CO frequency shifts are found in correspondence of Zr ions of the nanoparticles where the coordination is lower.

3.2 Basic Properties: Pyrrole Adsorption

To measure the Lewis basic properties of zirconia we have considered the adsorption of a pyrrole molecule. This molecule has been selected after having tried other potential molecular probes, such as CO2, CHCl3, SO2, BF3, and acetonitrile, but all these molecules tend to react with the zirconia surface, with bond breaking that prevents from a direct comparison of the various adsorption sites. Two types of interaction can be observed for pyrrole: one where the ring interacts with the metal cations in a flat orientation, dominated by dispersion forces, and a second one where the bonding occurs via formation of a hydrogen bond between the NH group of the pyrrole molecule and an oxygen ion of the surface. Both interactions have been observed in zeolites, and it has been reported that a large shift to lower frequencies of the NH vibration upon adsorption is almost entirely due to the formation of a hydrogen bond [57]. Figure 5a and b show the pyrrole ring interaction with the regular t-ZrO2 (101) and m-ZrO2 (\(\bar{1}11\)) surfaces, respectively, with adsorption energies of − 0.66 eV and − 0.81 eV, respectively.

Fig. 5
figure 5

Optimized structures of a pyrrole molecule interacting nearly parallel to the surface with a t-ZrO2 (101) and b m-ZrO2(\(\bar{1}11\)) surfaces and high coverage adsorption c–e on t-ZrO2 (101) surface. The blue, red, brown, gray and white spheres are Zr, O, C, N and H atoms, respectively. Distances in Angstrom

Full size image

On zirconia, at zero coverage, the flat bonding mode (ring interaction) is preferred compared to the formation of a hydrogen bond. However, things are different when more molecules are adsorbed in the supercell, modeling high coverage. Considering two co-adsorbed pyrrole molecules, Fig. 5c and d, the flat bonding mode is still preferred; however, with three co-adsorbed molecules Fig. 5e only the normal mode is stable due to steric effects. Thus, although adsorbed pyrrole molecules at low coverage prefer to stay parallel to the surface, Fig. 5a–c, at high coverage the upright adsorption mode is dominant Fig. 5e. We have considered the pyrrole bonded to the surface via the NH group as a probe molecule to explore the basicity of different oxygen atoms on the surface, Fig. 6. The data refer to the isolated pyrrole molecule, but since the intermolecular interactions are weak, the results are not expected to change as a function of coverage.

Fig. 6
figure 6

Optimal structures of pyrrole bound via NH to O ions on the regular (a–e) and the stepped (f–l) zirconia surfaces. a–c and f–h: m-ZrO2; d, e and i to l t-ZrO2. The blue, red, brown, gray and white spheres are Zr, O, C, N and H atoms, respectively

Full size image

3.2.1 Regular m-ZrO2 (\(\bar{1}11\)) and t-ZrO2 (101) Surfaces

There are 8 different oxygen atoms on the surface of m-ZrO2 (\(\bar{1}11\)), Fig. 1: O1 to O5 are on the surface while O6 to O8 are in the sub-surface, and cannot bind the pyrrole molecule. O1 is two coordinated (O2c) while the other oxygen anions (O2-O4) are O3c.

The adsorption energies (EADS) of the pyrrole bound via NH group to the surface O atoms go from − 0.42 to − 0.49 eV, see Table 2. These values are slightly smaller in absolute value than for the flat adsorption mode, Fig. 5. The distances of the H atom from the surface O ion are between 1.766 and 1.883 Å. Due to this interaction, the NH bond length slightly increases compared to the gas phase (1.013 Å) and the N–H stretching frequencies are significantly red-shifted by − 189 to − 380 cm−1, Table 2. This points to a different strength of the basic O sites on the surface. Thus, while the adsorption energies do not show a strong site-dependence, the N–H vibrational frequency does.

Table 2 Adsorption energy (EADS, eV), bond lengths (R, Å), N–H stretching frequencies (ν, cm−1), and 1H, 15 N and 17O NMR chemical shift (δiso, ppm) of pyrrole on ZrO2 surfaces and Zr16O32 and Zr40O80 nanoparticles
Full size table

In Fig. 7 we have plotted the Osurf-HNH bond distance, measuring the distance of the NH group of the pyrrole molecule from the surface, against the N–H vibrational frequency, potentially an observable quantity. The results show an almost linear correlation (R2 = 0.88) for the four O adsorption sites of the m-ZrO2 and t-ZrO2 surfaces. In particular, when the molecule goes closer to the surface, the NH stretching frequency exhibits a larger red-shift. This points to a more pronounced basic character of the O sites where this occurs. The bonding of pyrrole to the surface does not imply a charge transfer, as it is shown by the Bader charges. The charge on pyrrole due to the interaction with the surface is always smaller than 0.03 |e| in absolute value (Table S2).

Fig. 7
figure 7

Correlation between the shift in N–H stretching frequency, ΔνNH, and the distance of the pyrrole molecule from the O ion of the zirconia surface, RO-H

Full size image

Now we discuss the chemical shifts. 1H chemical shifts have been used to study the basicity of various sites in zeolites using pyrrole adsorption [26,27,28]. In these studies 1H chemical shifts of 9–11 ppm have been measured (slightly shifted with respect to the free molecule which has a value of 7.1 ppm), and a linear correlation with the proton affinity with the 1H chemical shift has been shown based on DFT calculations [26]. Here instead of the absolute value of the 1HN chemical shifts, δiso(1H), we discuss the change compared to the free molecule due to the adsorption on a basic site, Δδiso(1H). In our models Δδiso(1H) of adsorbed pyrrole is in the range + 5/ + 7 ppm, Table 2. We have plotted Δδiso(1H) against the pyrrole adsorption energy in Fig. 8. On the regular surfaces no clear trend emerges, due to the rather close values of both δiso(1H) and EADS. However, as it will be discussed below, a general although not regular tendency towards an increase of Δδiso(1H) for stronger surface-pyrrole bonds if found when all the other zirconia structures are considered, Fig. 8.

Fig. 8
figure 8

Correlation between the changes in 1H NMR chemical shift and the adsorption energy of the pyrrole molecule on various ZrO2 structures

Full size image

We consider now the changes in 15N NMR chemical shifts. Due to the low natural abundance of the 15N nucleus this is not easily accessible experimentally, although some examples have been reported in the literature [58]. As for the H case, also here we refer to the changes occurring on this property with respect to a free gas-phase pyrrole molecule. These changes, Δδiso(15N), for the regular surfaces go from + 21 to + 27 ppm, Table 2. If one plots these values for the five adsorption sites on the regular m-ZrO2 and t-ZrO2 surfaces versus the adsorption energy, an almost linear correlation is found, Fig. 9 (R2 = 0.92). In particular, an increase of the adsorption energy corresponds to an increase of the Δδiso(15N). However, if we include into this plot also the results of pyrrole adsorption on the stepped surfaces and on the nanoparticles (see below) the correlation becomes much worse and no simple trend can be established. We attribute this to the very different interaction of pyrrole on the regular surfaces and on the low-coordinated sites.

Fig. 9
figure 9

Correlation between the changes in 15N NMR chemical shift and the adsorption energy of the pyrrole molecule on the regular sites of m-ZrO2 and t-ZrO2 surfaces

Full size image

Recently, we have reported the measurement of the basicity of alkaline-earth oxide surfaces by means of 17O NMR calculations [59]. We found that the 17O NMR signal of the O ion directly bound to a probe molecule shifts considerably compared to the clean surface [59]. The average 17O NMR chemical shifts for the O atoms on the clean zirconia surfaces before and after adsorption of pyrrole are given in Table 2.

In Fig. 10 we have plotted the distance of the H atom of pyrrole from the surface, RO-H, versus Δδiso(17O). The plot shows a clear correlation of the two quantities, with stronger negative shifts of Δδiso(17O) in correspondence of shorter O–H distances (see squares in Fig. 10).

Fig. 10
figure 10

Correlation between the changes in 17O NMR chemical shift and the distance of pyrrole from the surface, RO-H, for various ZrO2 surfaces and nanoparticles

Full size image

The O ions involved in the bonding with pyrrole are shielded, and δiso(17O) decreases from − 21 to − 59 ppm with respect to δisoavg(17O) of the clean surfaces, see Table 2. Plotting Δδiso(17O) versus the change in N–H vibrational frequency, ΔνNH, we found a nearly linear correlation, see Table 2 and Fig. 11. This confirms that the 17O NMR signal of the O ion where a species is adsorbed can provide interesting information about the nature of the basic site, as found for the alkaline-earth oxides [59]. The full set of values of the 17O NMR chemical shifts is reported in the Supporting Information.

Fig. 11
figure 11

Correlation between the shift in N–H stretching frequency of the pyrrole molecule and the changes in 17O NMR chemical shift for pyrrole adsorbed on O ions of the regular and stepped m-ZrO2 and t-ZrO2 surfaces and on zirconia nanoparticles

Full size image

3.2.2 Stepped m-ZrO2 (\(\bar{2}12\)) and t-ZrO2 (134) Surfaces

Next, we consider pyrrole adsorption on both terrace and stepped O sites of m-ZrO2 (\(\bar{2}12\)) and t-ZrO2 (134) surfaces, Fig. 6 and Table 2. On the flat areas of the stepped surfaces the adsorption energies of pyrrole do not show significant changes with respect to the regular surface; the proximity of the step has practically no effect, due to the local character of the bond. Figure 6f shows the simultaneous formation of two hydrogen bonds of the pyrrole NH group with two O atoms; here the adsorption energy becomes − 0.58 eV. This stronger interaction does not correspond to a more pronounced variation of the N–H bond distance (elongated by 0.008 Å only with respect to the free molecule) and N–H stretching frequency (red-shifted by − 144 cm−1 with respect to gas-phase).

The adsorption of pyrrole on the steps of m-ZrO2 (\(\bar{2}12\)), Fig. 6g, and t-ZrO2 (134), Fig. 6i and j, show a different bonding mode. In these cases, in addition to the formation of a hydrogen bond of the pyrrole NH group, the pyrrole ring interacts via dispersion forces with the surface. This is similar to the bonding mode found for pyrrole in the cavity of zeolites containing trapped metal ions [57]. In these structures the bond strength increases considerably (− 1.08 eV for m-ZrO2 (\(\bar{2}12\)) and − 1.26 and − 1.15 eV for t-ZrO2 (134)), due to the multiple interaction mode. As found for zeolites [57], also here the changes of NH frequency are noticeable. ΔνNH on the stepped sites of m-ZrO2 (\(\bar{2}12\)), Fig. 6g, and t-ZrO2 (134), Fig. 6i and j is red-shifted by − 341, − 622 and − 221 cm−1, respectively. These values are not included in the correlation of Fig. 11 where the NH stretching frequencies are plotted versus the 17O chemical shift as the bonding mode is different.

The results of the 1H NMR show that in all structures the H atom of the NH group is deshielded by adsorption on the O ions of the surface, i.e. δiso goes to the lower fields. The maximum Δδiso(1H) is for pyrrole on O2c sites of regular, Fig. 6a, and stepped m-ZrO2 surfaces, Fig. 6f, + 7 and + 8 ppm, respectively. Δδiso(1H) for various O3c sites is + 5/ + 6 ppm, see Table 2. The Δδiso(1H) values for pyrrole adsorbed on the stepped surfaces have been included in Fig. 8. No clear trend emerges if one takes only these values, as similar chemical shifts of 5–6 ppm, correspond to adsorption energies from 0.3 to 0.5 eV.

More relevant is δiso(15 N) NMR as this has shown a linear correlation with EADS for adsorption on the regular zirconia surfaces, Fig. 9. On the models of the stepped surfaces, if we consider the flat regions, Fig. 6h, k, l, δiso(15 N) assumes similar values, + 19/ + 27 ppm, as on the regular surfaces. More pronounced are Δδiso(15 N) for the adsorption on the stepped sites, Fig. 6g, i and j + 40, + 38 and + 33 ppm, respectively. However, we did not include these data in the plot of Fig. 9 because of the different bonding mode.

The results of 17O NMR chemical shifts, Table 2, show that the surface O ions interacting with pyrrole are shielded, and δiso(17O) decreases by − 14/ − 56 ppm with respect to the δisoavg(17O) of the clean surfaces. However, for other structures, Fig. 6j, the O ion on the step interacting with NH is deshielded, and δiso increases by + 38, respectively, see also Fig. 10. This is due to the fact that pyrrole interacts with the surface via ring bonding mode, and the H-bonding becomes very long, 2.126 Å, Table 2.

The values of δiso(17O) for the stepped surfaces have been plotted against the N–H stretching frequency, Fig. 11, and the points are behaving as found for the regular surfaces, showing an overall linear trend. This reinforces the idea that δiso(17O) can be used to measure the basicity of sites where pyrrole binds via NH forming a hydrogen bond.

3.2.3 ZrO2 Nanoparticles

Here we consider pyrrole adsorption on the Zr16O32 and Zr40O80 nanoparticles. The interaction via the aromatic ring bound to Zr cations is clearly preferred, with adsorption energies of − 1.27 to − 1.70 eV Fig. 12.

Fig. 12
figure 12

The interaction of pyrrole ring with Zr16O32 nanoparticle. The blue, red, brown, gray and white spheres are Zr, O, C, N and H atoms, respectively. Distances in Angstrom

Full size image

This is much stronger than the formation of a hydrogen bond between the NH group of the pyrrole molecule and the O atoms of the nanoparticle (in the range − 0.32 to − 0.49 eV, Table 2 and Fig. 13a–g). So, one can rule out the possibility to experimentally test the basicity of the O2c or O3c surface ions by using pyrrole as a probe molecule. In some calculations we have been able to find a minimum structure for the H-bonded complex via NH group, with formation of a metastable complex. In other cases, however, the molecule does not bind via H but spontaneously binds in a flat mode. In this respect, the following discussion is purely hypothetical and the properties of the adsorbed pyrrole molecule, Table 2, represent an internal test of the different nature of the surface O atoms. For instance, the N–H stretching frequencies for the adsorbed molecules have been plotted against the distance of pyrrole from the surface of the nanoparticle, RO-H, Fig. 7, showing the same trend found for the other O sites of the flat and stepped zirconia surfaces.

Fig. 13
figure 13

Optimal structures of hydrogen bonded pyrrole via NH group with the O atoms of the surface of Zr16O32 (a–c) and Zr40O80 (d–g) nanostructures. The blue, red, brown, gray and white spheres are Zr, O, C, N and H atoms, respectively

Full size image

We also computed Δδiso(1H), Δδiso(15N) and Δδiso(17O) NMR chemical shifts (see also Supplementary Information), and we reported these values in the corresponding curves. They will be discussed in the concluding section.

4 Conclusions

In this work we have investigated the acid and base sites on monoclinic and tetragonal zirconia using DFT derived IR and NMR properties of adsorbed probe molecules. To this end, regular and stepped surfaces of m- and t-ZrO2 as well as stoichiometric zirconia nanoparticles have been considered. Acidity and basicity were probed by the adsorption of CO and pyrrole molecules, respectively. The average adsorption energy of CO on the different sites of regular and stepped m- and t-ZrO2 surfaces is about − 0.52 eV, and increases slightly for nanoparticles (− 0.66 eV). The adsorption energy of CO shows a correlation with the C–O stretching frequency. In particular, the blue-shift of the CO stretching mode, indicating a stronger Zr acid site, increases moving from the regular surfaces to the stepped surfaces and the nanoparticles. This confirms the potential use of CO as a probe to measure the acidic character of cation sites on the surface of zirconia.

The results of NMR calculations show that the C atom of adsorbed CO is shielded and δiso(13C) goes to the higher field, but the shifts are very small and no direct correlation with the surface acidity can be established.

Pyrrole has been used to monitor the surface basicity [26,27,28]. In zeolites this has been used as a probe molecule to titrate the basic character of O ions of the cages [57]. Pyrrole can interact with oxide surfaces in two different bonding modes, with the center of the ring close to a cation or with the NH group pointing to a surface anion. Only this second bonding mode is of some interest for the study of surface basicity. Unfortunately, for all ZrO2 structures considered, the ring interaction, dominated by polarization and dispersion forces, is stronger. Bonding via the NH group become preferred at high coverage, due to steric effects, which allows a theoretical study of the properties.

A series of correlations have been studied that can be useful for the identification of the strength of the basic sites. An almost linear correlation with good regression coefficient, R2 = 0.88, is found between the NH vibrational frequency and the distance of the pyrrole molecule from the O ion of the surface, RO-H, Fig. 7. On the contrary, no correlation exists with the strength of the adsorption energy. Similar correlations have been analyzed for the NMR chemical shifts.

The 1H signal of the proton in contact with the surface shows a general trend, with more positive shifts corresponding to stronger adsorption energies of the pyrrole molecule, Fig. 8. However, the data points for the various structures considered are rather scattered, and this cannot be taken as a robust descriptor of the strength of the basic site.

A higher correlation is found for the 15N chemical shift, in particular if we plot this versus the pyrrole adsorption energy on the O sites on the regular m-ZrO2 and t-ZrO2 surfaces, Fig. 9. Here the regression is very good, with R2 = 0.92. If we consider all the structures studied, we still find a linear trend, even including some structures where the pyrrole molecule is not only bound via H-bonding, see Fig. S4.

We recently showed that the 17O NMR chemical shift can provide in principle useful information about the basic character of surface sites in alkaline-earth oxides [59]. Here we confirm this potential role. In fact, while no direct correlation exists between δiso(17O) NMR of the O ion directly bound to the pyrrole molecule and the adsorption energy, an almost linear correlation if found when we plot this quantity versus the distance of the molecule from the surface, RO-H, Fig. 10. The R2 value is not particularly high, 0.78, but this also partly due to the flat nature of the potential energy surface, which results in some uncertainty on the computed O–H distances.

Finally, a good correlation is found between the two key quantities that can be used to titrate the basic character of the surface using pyrrole adsorption: the N–H stretching frequency and the 17O NMR chemical shift, Fig. 11. The two quantities show a nice linear correlation despite the very irregular nature of some of the structures considered. This confirms that these two properties can provide in principles useful information about the basic character of various O sites on the surface of zirconia.