1 Introduction

It is well established that when a low-viscosity fluid such as water is injected into a porous rock matrix saturated with a higher-viscosity fluid such as crude oil, patterns of viscous fingering occur (Homsy 1997; Måløy et al. 1985; Chen and Wilkinson 1985; Lenormand et al. 1988), namely the formation of patterns at the unstable interface between the two fluids in the porous medium (typically, patterns of narrow tendrils of the injected fluid in the porous medium). This is an interesting physical phenomenon with immense practical implication to enhanced oil recovery (EOR) where water is injected into one well to help evaculate the oil from the hydrocarbon reservoir into an adjacent production well. The displacement morphology of immiscible fluid displacement in a porous medium is complex and is affected by many parameters of the fluids including the viscosity ratio of the two fluids and the wettability. Wettability relates to the degree the invading fluid is attracted to the rock grains relative to itself. For example, a non-wetting fluid is attracted to itself much more than to the solid, and hence, a droplet of this fluid will form on a solid surface. The angle of the fluid interface relative to the solid surface is called the wetting angle. A wetting angle approaching \(180^\circ\) means that the droplet is almost circular in 2D (spherical in 3D), and such fluids are termed non-wetting. The opposite case is a highly wetting fluid where the fluid droplet flattens by gravity and the angle between the fluid interface and solid approaches \(0^\circ\). Our aim here is to apply the lattice Boltzmann method to the study of immiscible flow patterns such as viscous fingering at the pore scale in a 2D model of a porous medium. In particular, we aim to study the effect of the wetting angle and viscosity ratio on the viscous fingering and the saturation at breakthrough or sweep, which directly relates to the oil “Recovery Factor” in EOR. In the field of petroleum engineering, it is well accepted that the wettability is a crucial factor for EOR (Deng et al. 2020), and while the relationship between wettability and recovery factors is known to be complex, there is a general consensus based on extensive research that the recovery factor increases as the invading fluid becomes more wetting (Deng et al. 2020).

There have been many studies, experimental, theoretical and numerical, on the influence of wettability on the pattern of flow in porous media. For example, Stokes et al. (1986) found in experimental work that wettability affects the finger width. Cieplak and Robbins (1988, 1990) developed a numerical model for quasi-static fluid–fluid displacement and conducted numerical experiments of flow in a 2D array of discs and found that as the wetting angle decreases (wettability increases), a progressive smoothing mechanism occurs and that the width of invading fingers seems to diverge beyond a critical angle which depends on porosity. Trojer et al. (2015) conducted a systematic experimental study of fluid–fluid displacement in a granular pack and found that wettability profoundly affects the invasion morphology. Namely, they observed a compactification of viscous fingering and a regime of compact displacement at low capillary numbers for weak imbibition. Zhao et al. (2016) found, in microfluidic experiments involving vertical posts representing a porous medium, that as wettability is increased, there is more efficient displacement and higher saturation up until a critical angle is reached, beyond which the system undergoes a wetting transition and the trend is reversed. Research using an invasion-percolation model by Primkulov et al. (2018) extended the Cieplak and Robbins description of quasistatic fluid invasion reproducing the wetting transition in strong imbibition (Cieplak and Robbins 1988, 1990). A large number of core-scale experiments have shown improved displacement efficiency when the system’s wettability is altered towards imbibition, either by the addition of surfactants or by the use of low-salinity waterflooding (Kennedy et al. 1955; Jadhunandan and Morrow 1995; Seethepalli et al. 2004; Morrow and Buckley 2011; Sharma and Mohanty 2013).

In this paper, we aim to study the complex relationship between saturation at breakthrough (sweep) with the viscosity ratio \(M = \nu _1/\nu _2\) and wetting angle \(\theta _\mathrm{w}\). To achieve this goal, we conduct a suite of 189 simulations of pore-scale two-phase flow in a simplified 2D model of a porous rock matrix and plot the flow patterns at a range of \((M,\theta _\mathrm{w}\)) pairs, and a phase space plot of saturation as a function of viscosity ratio M and wetting angle \(\theta _\mathrm{w}\). The simulations are carried out using the Rothman–Keller colour gradient multiphase lattice Boltzmann method (Latva-Kokko and Rothman 2005), which enables accurate pore-scale simulations to be conducted of two-phase immiscible fluid flow. Although our simulations are only in 2D, we believe that the general conclusions should be applicable to realistic 3D media, although details will certainly change. However, large-scale 3D numerical experiments and laboratory studies will be required to validate whether this is born out before one could reliably make conclusions pertaining to 3D media.

2 Numerical Simulation Methodology

In this paper, we apply the Rothman–Keller (RK) colour gradient multiphase lattice Boltzmann method of Latva-Kokko and Rothman (2005), which enables pore-scale two-phase flow of immiscible fluids in complex porous media to be simulated, where the fluids are allowed to have different densities and viscosities, with viscosity contrasts allowed as high as 100 or more. The capability of the RK LBM to model high-viscosity contrasts is required for our study, whereas the other widely applied multiphase LBM due to Shan and Chen (Shan and Chen 1993) is only able to model relatively small viscosity contrasts. Furthermore, the RK LBM enables the wetting angle to be specified so studies can be conducted of the effect of the wetting angle and viscosity ratio on viscous fingering.

The RK LBM for immiscible fluid flow involves solving for number densities \(f_\alpha ^1\) and \(f_\alpha ^2\) of two fluids (red and blue) moving in the \(\alpha\)-direction on a discrete lattice in four steps, which are the streaming step given by

$$\begin{aligned} f_\alpha ^k ( \mathbf{x} , t ) \ = \ f_\alpha ^k ( \mathbf{x} - \mathbf{c}_\alpha \varDelta t , t - \varDelta t) ,\end{aligned}$$
(1)

where k denotes the fluid (1=red, 2=blue) and \(\varDelta t\) is the time step, followed by two collision steps, which can be written as

$$\begin{aligned} f_\alpha ^{k*} ( \mathbf{x},t) \ = \ f^{k} (\mathbf{x},t) \ + \ (\varDelta f_\alpha ^k )^1 \ + \ (\varDelta f_\alpha ^k )^2, \end{aligned}$$
(2)

where the superscript \(^*\) denotes the post-collision distributions, and \((\varDelta f_\alpha ^k)^1\) and \((\varDelta f_\alpha ^k)^2\) are the two collision terms, which represent how the particle distributions change during each time step due to collision \((\varDelta f^k_\alpha )^1\), while encouraging colour segregation \((\varDelta f^k_\alpha )^2\), and finally a “recolouring” step which achieves separation of the two fluids given by

$$\begin{aligned} f_\alpha ^1 \ = \ {\rho _1 \over \rho } f_\alpha ^* \ + \ \beta {{\rho _1 \rho _2}\over \rho ^2} f_\alpha ^{eq} (\rho , \mathbf{u} = 0) \cos (\lambda _\alpha ), \end{aligned}$$
(3)

and

$$\begin{aligned} f_\alpha ^2 \ = \ {\rho _2 \over \rho } f_\alpha ^* \ - \ \beta {{\rho _1 \rho _2}\over \rho ^2} f_\alpha ^{eq} (\rho , \mathbf{u} = 0) \cos (\lambda _\alpha ), \end{aligned}$$
(4)

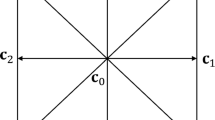
where \(f^*_\alpha = \sum _k f^{k*}_\alpha\), \(f^{eq}_\alpha (\rho ,\mathbf{u}=0)\) is the standard equilibrium distribution at zero velocity (Huang et al., 2015 Huang et al. (2015)), \(\rho _k\) is the macroscopic density of fluid k, \(\rho\) is the total macroscopic density, \(\lambda _\alpha\) is the angle between the “colour gradient” \(\mathbf{F}(\mathbf{x},t)\) and the velocity vector \(\mathbf{c}_\alpha\), \(\beta\) is a model parameter that affects interface thickness and is typically set to 0.5, and \(\mathbf{c}_\alpha\) is the velocity vector that moves number densities orthogonally or diagonally in a 2D Cartesian grid by one lattice spacing in one time step and is given by

$$\begin{aligned}&\mathbf{c}_\alpha = [(0,0), (1,0), (-1,0), (0,1), (0,-1),\\&\quad (1,1), (-1,-1), (1,-1), (-1,1)]\varDelta x/\varDelta t, \end{aligned}$$

where \(\varDelta x\) is the lattice spacing and \(\varDelta t\) is the time step.

The first collision term has the same form as the standard BGK (single relaxation time) LBM collision term (Qian et al. 1992; Chen and Doolen 1998) and has the effect of causing the number densities to relax towards the equilibrium distribution. The first collision term is given by

$$\begin{aligned} (\varDelta f_\alpha ^k )^1 \ = \ {1 \over \tau } \left( f_\alpha ^{k,\mathrm{eq}} (\mathbf{x},t) \ - \ f_\alpha ^{k} (\mathbf{x},t) \right) \end{aligned}$$
(5)

where \(\tau\) is the relaxation time and \(f_\alpha ^{k,\mathrm{eq}} (\mathbf{x},t)\) is the equilibrium distribution, which is the same as the standard distribution except for the rest factor which depends on the fluid densities (Grunau et al. 1993). The relaxation time for fluid k is calculated in the standard way as

$$\begin{aligned} \tau _k \ = \ {\nu _\mathrm{k} \over {c_s^2 \varDelta t}} \ + \ 0.5, \end{aligned}$$
(6)

where the relaxation time \(\tau\) in Eq. (5) of the LBM is varied smoothly at the interface between the two fluids according to Grunau et al. (1993) using the standard value of the free parameter \(\delta = 0.98\).

The second collision term, which encourages colour segregation, is given by Reis and Phillips (2007)

$$\begin{aligned} (\varDelta f_\alpha ^k )^2 \ = \ A | \mathbf{F}| \left( w_\alpha (\cos (\lambda _\alpha )|\mathbf{c}_\alpha |)^2 - B_\alpha \right), \end{aligned}$$
(7)

where \(w_\alpha\) are the standard Lattice Boltzmann weights, A is a parameter that controls the interfacial tension and \(B_\alpha\) are specified constants.

The colour gradient \(\mathbf{F} (\mathbf{x},t)\) is calculated according to the method of Mora et al. (2020), which optimizes isotropy of the gradient, namely

$$\begin{aligned} \mathbf{F} ( \mathbf{x} ,t) \ = \ \sum _\alpha b_\alpha \mathbf{c}_\alpha \left( \rho _1 ( \mathbf{x} + \mathbf{c}_\alpha \varDelta t,t) - \rho _2 ( \mathbf{x} + \mathbf{c}_\alpha \varDelta t,t)\right), \end{aligned}$$
(8)

where the \(b_\alpha\) are scalar coefficients of the second-order finite difference approximation of the gradient given by Mora et al. (2020) that is second-order accurate and maximizes isotropy. Namely,

$$\begin{aligned} b_\alpha \ = \ \left\{ \begin{array}{ll} 1 / W &{},\alpha \ = \ 1,2,3,4 \\ w / W &{},\alpha \ = \ 5,6,7,8 \end{array} \right., \end{aligned}$$
(9)

where the scale factor W is given by

$$\begin{aligned} W \ = \ 2 + 4w, \end{aligned}$$
(10)

and the diagonal weighting term is set to \(w=0.3\), which optimizes isotropy of the colour gradient calculation.

In the colour gradient LBM, the density of each fluid is calculated using

$$\begin{aligned} \rho _k \ = \ \sum _\alpha f^k_\alpha, \end{aligned}$$
(11)

and the macroscopic density and momentum density of the fluid are given by

$$\begin{aligned} \rho \ = \ \sum _k \rho _k, \end{aligned}$$
(12)

and

$$\begin{aligned} \rho \mathbf{u} \ = \ \sum _k \sum _\alpha f_\alpha ^k \mathbf{c_\alpha }, \end{aligned}$$
(13)

The relaxation time in Eq. (5) relates to the kinematic viscosity \(\nu _\mathrm{k}\) of each fluid as follows

$$\begin{aligned} \nu _\mathrm{k} \ = \ c_s^2 ( \tau _k - 0.5) \varDelta t, \end{aligned}$$
(14)

where \(c_s = \varDelta x / (\sqrt{3} \varDelta t)\) is the speed of sound in the lattice, and an interpolation algorithm is used to ensure that the relaxation time varies smoothly to avoid abrupt changes, which are not handled well by the LBM (Grunau et al. 1993).

Solid regions can be modelled by “bounce-back” boundary conditions in which particle number densities are reflected back from where they came from when they encounter a solid region. The wetting angle \(\theta _\mathrm{w}\) is specified by setting the densities of the two fluids in the solid region (Latva-Kokko and Rothman 2005) through

$$\begin{aligned} \theta _\mathrm{w} \ = \ \cos ^{-1} \left( {\rho _{w1} - \rho _{w2} } \over \rho _i \right), \end{aligned}$$
(15)

3 Simulation Setup and Suites

We initialized a simplified 2D model of a porous medium in a square region of size \(300 \times 300\) pixels by randomly dropping non-overlapping random-sized solid circular particles with radii ranging from \(r=5 \varDelta x\) through \(r=15 \varDelta x\), with a minimum separation of \(4 \varDelta x\). This initialization is similar to that used in a study of viscous and capillary fingering by Huang et al. (2014), and in particular, we use the same minimum spacing between grains as used by Huang et al. This minimum value ensures that our 2D porous medium is permeable with no blocked regions, which attempts to mimic the 3D case where tortuosity ensures there are always flow pathways around grains for course-grained samples like sandstones.

Figure 1 shows the model rock matrix that is used in the following simulations. The pore space in the model was saturated with a blue fluid, and a red fluid was injected from the left side of the model using (Zou and He 1997) boundary conditions to specify a constant inlet velocity at the left edge of the model and a constant pressure at the right edge of the model. The density of the two fluids was set to \(\rho _1 = \rho _2 = 1\) because the small \(\sim\) 10% density contrast between crude oil and water plays no role in viscous fingering in EOR. The surface tension parameter A in Eq. (7) was set such that all simulations were performed at a high capillary number of \(\mathrm{Ca} \sim 10\), which ensures that viscous forces dominate over capillary forces, and hence, the simulations are in the viscous fingering regime. The capillary number is defined as

$$\begin{aligned} \mathrm{Ca} \ = \ {{\mu _\mathrm{r} u_\mathrm{in}}\over {\sigma }} \ = \ {{\rho _\mathrm{r} \nu _\mathrm{r} u_\mathrm{in}}\over {\sigma }}, \end{aligned}$$
(16)

where \(\mu _\mathrm{r}\) is the dynamic viscosity of fluid 1 = red fluid, \(u_\mathrm{in}\) is the inlet velocity, \(\rho _\mathrm{r}\) is the density of the red fluid, and \(\sigma = \alpha A\) is the interfacial tension where numerical studies have shown that \(\alpha \in [0.55,0.79]\) for a wide range of viscosities of the two fluids in the model (Mora et al. 2020). In the simulations, we set the inlet velocity \(u_\mathrm{in}\) such that the simulations are performed at a sufficiently low Reynolds number such as \(\mathrm{Re} \sim 0.2\)—well below the critical Reynolds number for turbulence of \(\mathrm{Re} \sim 2300\)—which ensures that inertial effects and turbulence are negligible in the simulations. Namely, the Reynolds number is defined as

$$\begin{aligned} \mathrm{Re} \ = \ {{u D}\over \nu }, \end{aligned}$$
(17)

where D is the characteristic scale length, \(\nu\) is the kinematic viscosity, and u is the flow speed. Hence, the inlet velocity can be set such that \(\mathrm{Re} = 0.2\) using

$$\begin{aligned} u_\mathrm{in} \ = \ {{\mathrm{Re} \min (\nu _\mathrm{r},\nu _\mathrm{b})}\over D} \ = \ 0.05 \min (\nu _\mathrm{r},\nu _\mathrm{b}), \end{aligned}$$
(18)

where we assume \(D=4 \varDelta x\), i.e. we set D to be the throat width in the porous medium. Once we have set the inlet velocity, we can calculate the surface tension required to achieve a capillary number of 10 by rearranging Eq. (16), which leads to

$$\begin{aligned} \sigma \ = \ \alpha A \ = \ {{\rho _\mathrm{r} \nu _\mathrm{r} u_\mathrm{in}}\over \mathrm{Ca}} \ = \ {{\nu _\mathrm{r} u_\mathrm{in}}\over \mathrm{Ca}}, \end{aligned}$$
(19)

and hence, using \(\alpha \sim 0.55\), we can estimate the interfacial tension parameter A in the model.

Finally, we must select the viscosities of the two fluids in the numerical model denoted \(\nu _\mathrm{r}\) and \(\nu _\mathrm{b}\) to enable simulations over the desired range of viscosity ratios \(M = \nu _\mathrm{r}/\nu _\mathrm{b} \Rightarrow \nu _\mathrm{r} = M \nu _\mathrm{b}\). This is achieved by choosing the product of viscosities to be \(\nu _\mathrm{r} \nu _\mathrm{b} = (0.2)^2\). With this choice, one can calculate the two viscosities from the desired viscosity ratio via

$$\begin{aligned} \nu _\mathrm{r} \nu _\mathrm{b} \ = \ M \nu _\mathrm{b}^2 \ = \ 0.2^2 \ \Rightarrow \ \nu _\mathrm{b} \ = \ \sqrt{0.2^2/M},\mathrm{and},\nu _\mathrm{r} = M \nu _\mathrm{b}, \end{aligned}$$
(20)

The above choice of how to select viscosities enables stable and accurate simulations to be performed of the desired viscosity ratio with the RK colour gradient multiphase lattice Boltzmann method.

In the following, we conducted a suite of 189 simulations spanning 9 wetting angles from non-wetting (\(\theta _\mathrm{w} = 180^\circ\)) through to perfectly wetting (\(\theta _\mathrm{w} = 0^\circ\)) at intervals of \(22.5^\circ\), and 21 viscosity ratios spanning 5 orders of magnitude, namely \(M = \nu _\mathrm{r}/\nu _\mathrm{b} \in [0.001,\ldots ,100]\)) at intervals of \(\varDelta \log _{10} M = 0.25\). Each simulation was started with the porous medium saturated by the blue fluid. The red fluid was then injected from the left, and the simulation was stopped when the red fluid breaks through the right boundary, which was defined as when the red fluid density reached 98% anywhere along the right edge of the model.

Fig. 1
figure 1

The model porous rock matrix

Full size image

4 Results

Figure 2 shows plots of the fluid flow at breakthrough for three wetting angles corresponding to non-wetting (\(\theta _\mathrm{w}=180^\circ\)), partially wetting (\(\theta _\mathrm{w}=90^\circ\)), and perfectly wetting (\(\theta _\mathrm{w} = 0^\circ\)) and for various viscosity ratios from \(M=0.001\) through \(M=100\). For low-viscosity ratios \(M \ll 0.1\), we observe viscous fingering—narrow tendrils of the red fluid (black fluid on the plots) that span the model. As the viscosity ratio approached unity, the fluid displacement morphology transforms into a deformed linear front, and for high-viscosity ratios \(M=100\), we see stable displacement. One also observes that the morphology of the fingering is affected by the wetting angle. For the non-wetting case, the fingers are narrow, whereas for the wetting case with \(\theta _\mathrm{w}=0^\circ\), we observe somewhat more rounded and broader fingers for the low-viscosity cases with \(M \le 0.01\) in agreement with the work of Stokes et al. (1986) and Cieplak and Robbins (1988, 1990)

Figure 3 shows a phase-space \(S(M,\theta _\mathrm{w})\) plot of the saturation level at breakthrough (sweep) for the 189 runs, which allows one to view how the sweep varies with viscosity ratio M and wetting angle \(\theta _\mathrm{w}\), as well as the phase space difference \(\varDelta S(M,\theta _\mathrm{w})\), which is defined as the difference between the saturation at each \((M,\theta _\mathrm{w})\) pair relative to the saturation at the same M of a non-wetting fluid. Namely, the saturation difference is defined as

$$\begin{aligned} \varDelta S ( M, \theta _\mathrm{w}) \ = \ S(M,\theta _\mathrm{w}) \ - \ S(M,180^\circ ), \end{aligned}$$
(21)

and measures how much more or less saturated the model is at a given \((M,\theta _\mathrm{w}\)) pair relative to the saturation for a non-wetting fluid with \(\theta _\mathrm{w} = 180^\circ\) at the same viscosity ratio M, thereby highlighting the effect of wetting angle on the saturation at breakthrough. The dominant feature on the saturation plot is that the saturation is low at small viscosity ratios (\(M \ll 1\)) and becomes high for large viscosity ratios (\(M>1\)). For example, at \(M=0.001\), the saturation is 35–40%, and saturation approaches unity at large viscosity ratios (\(M\sim 100\)). On the plot of the saturation difference \(\varDelta S\), one observes some tendency for the saturation to be higher for more wetting fluids, but not always, and the phase space landscape is complex with hills and valleys. For example, we observe a hill in the saturation difference centred on a viscosity ratio of \(M=0.01\) and \(\theta _\mathrm{w} = 22.5^\circ\). The maximum in saturation at (\(M,\theta _\mathrm{w}) = (0.01,22.5^\circ )\) is 49.5% compared to a saturation of 38.7% for a non-wetting fluid at this viscosity ratio, i.e. when \((M,\theta _\mathrm{w}) = (0.01,180^\circ )\). Hence, the saturation at the optimal wetting angle of \(\theta _\mathrm{w}=22.5^\circ\) for viscosity ratio of \(M =0.01\) is \(49.5/38.7 = 1.28\) times larger than the saturation for a non-wetting fluid at this viscosity ratio or 28% higher. In contrast, at the smallest viscosity ratio of \(M=0.001\), we see a decrease in saturation with wettability as the wetting angle decreases from \(\theta _\mathrm{w}=180^\circ\) down to a minimum in saturation at \(\theta _\mathrm{w} \sim 67.5^\circ\), followed by a modest increase back upwards such that the saturation for the fully wetting case is approximately the same as the saturation for the non-wetting case. And at a modestly small viscosity ratio of \(M\sim 0.3 \Rightarrow \log _{10} M \sim -0.5\), there is little change in saturation with wetting angle with only a minor decrease in saturation for more wetting fluids. For larger viscosity ratios with \(M \ge 1\), we observe a broad hill in saturation for mixed wetting to wetting fluids at wetting angles \(\theta _\mathrm{w} < 135^\circ\).

The phase space plot of the saturation difference clearly shows that saturation is not a simple function of wetting angle and viscosity ratio and indicates that the flow morphology and saturation relate to the hydrodynamical parameters and geometrical model in a complex manner. Whether or not saturation increases with wettability depends on the interplay between the pore geometry and the effects of the viscosity ratio and the wetting angle. We can see that for the specific case of our rock matrix, the sweep (yield) is maximized at a specific wetting angle when the viscosity ratio is \(M=0.01\). And at other viscosity ratios with \(M<1\), the wetting angle has less effect and at \(M=0.001\), there is a minimum in saturation at intermediate wetting angles, so sweep is maximized with either a perfectly wetting or a non-wetting fluid at this viscosity ratio.

Clearly, the landscape and features in the saturation difference plot will depend on the statistics and details of the pore space model, and how these interact with the dynamics of multiphase flow at any given wetting angle and viscosity ratio. With large enough computational resources, it should be possible to digitize a significant 3D volume of a given reservoir rock and map out the saturation phase space and to use this as a means of selecting the wetting angle that will maximize production for this field’s crude oil (i.e. the wetting angle that optimizes yield will depend on the viscosity ratio and hence the viscosity of the crude oil of the field).

Fig. 2
figure 2

Snapshots showing the invading fluid at the moment of breakthrough for various viscosity ratios \(M \in [0.001,100]\) and three different wetting angles \(\theta _\mathrm{w}\). The black region indicates the red invading fluid

Full size image
Fig. 3
figure 3

Phase space showing the saturation S at the moment of breakthrough as a function of viscosity ratios and wetting angles (left) and phase space showing the difference in the saturation \(\varDelta S\) at the moment of breakthrough as a function of viscosity ratios and wetting angles relative to the saturation at a wetting angle of \(\theta _\mathrm{w}=180^\circ\)

Full size image

5 Conclusions

We have conducted a suite of 189 simulations of immiscible fluid flow in a 2D porous medium using the colour gradient multiphase lattice Boltzmann method to study how the morphology of flow and saturation at breakthrough is affected by the viscosity ratio M and wetting angle \(\theta _\mathrm{w}\). Each of the 189 simulations involved injecting a “red fluid” at the left of a square 2D model rock matrix saturated with a “blue fluid” at a constant rate until the red fluid reaches the right side of the model which is termed breakthrough. The morphology of the flow and ultimately, the saturation at breakthrough, is of great practical significance to EOR and provides a measure of how much of the blue fluid is displaced from the model rock matrix and hence the oil recovery factor. As expected, we observe narrow viscous fingers for low-viscosity ratios when a non-wetting low-viscosity fluid is injected into the model and somewhat broader rounded fingers for injecting a wetting fluid. The dominant effect on the saturation is the viscosity ratio, with narrow fingers and consequently low saturations when the viscosity ratio is small (\(M \ll 1\)), and stable displacement of a deformed front of red fluid and high saturations when the viscosity ratio is high (\(M > 1\)). A wealth of petroleum engineering research has shown that the wettability plays a vital role on determining the saturation at breakthrough, with the general conclusion that the saturation increases with wettability. We have plotted the phase space of saturation at breakthrough as a function of viscosity ratio and wetting angle and found that the phase-space landscape is complex. While there is some tendency for saturation to increase with wettability at least for certain viscosity ratios such as for \(M>0.3\) and \(M=0.01\), the landscape has hills and valleys, particularly for low-viscosity ratios \(M<1\). For example, at a viscosity ratio of \(M=0.01\), there is an overall trend of increased saturation with wettability, but the maximum saturation occurs at \(\theta _\mathrm{w} = 22.5^\circ\) rather than for a perfectly wetting fluid with \(\theta _\mathrm{w}=0^\circ\). And at a viscosity ratios of \(M=0.001\), there is no tendency for saturation to increase with wettability. Rather, we observe a minimum in saturation at \(\theta _\mathrm{w} = 67.5^\circ\) for our specific 2D model of a porous medium.

Future work is required to understand the complex relationship between viscous fingering morphology and saturation at breakthrough, and the wettability, viscosity ratio and porous medium geometry. Furthermore, as this paper involves small-scale 2D simulations of immiscible two-phase flow in a porous medium, research using larger scale and 3D models is required to verify how our 2D conclusions translate to realistic 3D examples, and experimental validation is required to ensure the numerical results can be reliably applied to real cases. This is particularly so given that our simulations were done at significantly higher capillary numbers than those in microfluidic laboratory experiments and field studies.