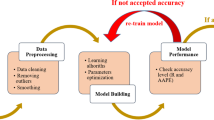
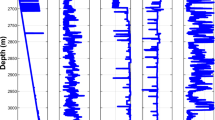
Abstract
The objective of this work is to study the applicability of various machine learning algorithms for the prediction of some rock properties which geoscientists usually define due to special laboratory analysis. We demonstrate that these special properties can be predicted only basing on routine core analysis (RCA) data. To validate the approach, core samples from the reservoir with soluble rock matrix components (salts) were tested within 100 + laboratory experiments. The challenge of the experiments was to characterize the rate of salts in cores and alteration of porosity and permeability after reservoir desalination due to drilling mud or water injection. For these three measured characteristics, we developed the relevant predictive models, which were based on the results of RCA and data on coring depth and top and bottom depths of productive horizons. To select the most accurate machine learning algorithm, a comparative analysis has been performed. It was shown that different algorithms work better in different models. However, two-hidden-layer neural network has demonstrated the best predictive ability and generalizability for all three rock characteristics jointly. The other algorithms, such as support vector machine and linear regression, also worked well on the dataset, but in particular cases. Overall, the applied approach allows predicting the alteration of porosity and permeability during desalination in porous rocks and also evaluating salt concentration without direct measurements in a laboratory. This work also shows that developed approaches could be applied for the prediction of other rock properties (residual brine and oil saturations, relative permeability, capillary pressure, and others), of which laboratory measurements are time-consuming and expensive.













Similar content being viewed by others
References
Andersen, M.A., Duncan, B., McLin, R.: Core truth in formation evaluation. Oilfield Rev. 82(2), 16–25 (2013)
API: Recommended practices for core analysis. American Petroleum Institute, Washington, DC (1998)
Bergstra, J., Bengio, Y.: Random search for hyper-parameter optimization. J. Mach. Learn. Res. 13(1), 281–305 (2012)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001)
Breiman, L.: Classification and Regression Trees. Routledge, London (2017)
Carman, P.C.: Flow of Gases Through Porous Media. Academic Press, London (1956)
Chen, T., Guestrin, C.: Xgboost: a scalable tree boosting system. In: Conference on Knowledge Discovery and Data Mining, ACM, pp. 785–794 (2016)
Choubineh, A., Helalizadeh, A., Wood, D.A.: Estimation of minimum miscibility pressure of varied gas compositions and reservoir crude oil over a wide range of conditions using an artificial neural network model. Adv. Geo-Energy Res. 3(1), 52–66 (2019)
Cortes, C., Vapnik, V.: Support vector networks. Mach. Learn. 20(3), 273–297 (1995)
Crammer, K., Singer, Y.: On the algorithmic implementation of multiclass kernel-based vector machines. J. Mach. Learn. Res. 2(Dec), 265–292 (2001)
Dandekar, A.: Petroleum Reservoir Rock and Fluid Properties. Taylor & Francis, London (2006)
Freedman, D.A.: Statistical Models: Theory and Practice. Cambridge University Press, Cambridge (2009)
Friedman, J.: Greedy function approximation: a gradient boosting machine. Ann. Stat. 29(5), 1189–1232 (2001)
Gaafar, G.R., Tewari, R.D., Zain, Z.M., et al.: Overview of advancement in core analysis and its importance in reservoir characterisation for maximising recovery. In: SPE Asia Pacific Enhanced Oil Recovery Conference, Society of Petroleum Engineers (2015)
Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Series in Statistics. Springer, Berlin (2001)
Haykin, S.: Neural Networks: A Comprehensive Foundation, 2nd edn. Prentice Hall PTR, Upper Saddle River (1998)
Ho, T.K.: Random decision forests. In: Proceedings of 3rd International Conference on Document Analysis and Recognition, IEEE, vol. 1, pp. 278–282 (1995)
Hsieh, C.J., Chang, K.W., Lin, C.J., Keerthi, S.S., Sundararajan, S.: A dual coordinate descent method for large-scale linear SVM. In: Proceedings of the 25th International Conference on Machine Learning, ACM, pp. 408–415 (2008)
Kotsiantis, S.B., Zaharakis, I., Pintelas, P.: Supervised machine learning: a review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 160, 3–24 (2007)
Liu, Z., Herring, A., Arns, C., Berg, S., Armstrong, R.T.: Pore-scale characterization of two-phase flow using integral geometry. Transp. Porous Media 118(1), 99–117 (2017)
Mahzari, P., AlMesmari, A., Sohrabi, M.: Co-history matching: a way forward for estimating representative saturation functions. Transp. Porous Media 125(3), 483–501 (2018)
McCulloch, W.S., Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5(4), 115–133 (1943)
McPhee, C., Reed, J., Zubizarreta, I.: Core Analysis: A Best Practice Guide, vol. 64. Elsevier, Amsterdam (2015)
Meshalkin, Y., Koroteev, D., Popov, E., Chekhonin, E., Popov, Y.: Robotized petrophysics: machine learning and thermal profiling for automated mapping of lithotypes in unconventionals. J. Pet. Sci. Eng. 167, 944–948 (2018)
Monicard, R.P.: Properties of Reservoir Rocks: Core Analysis, vol. 5. Editions Technip, Paris (1980)
Orlov, D., Koroteev, D., Sitnikov, A.: Self-colmatation in terrigenic oil reservoirs of Eastern Siberia. J. Pet. Sci. Eng. 163, 576–589 (2018)
Ottesen, B., Hjelmeland, O.: The value added from proper core analysis. In: International Symposium of the Society of Core Analysts, Abu Dhabi, UAE, Weatherfordlabs, vol. 29 (2008)
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., Duchesnay, E., Louppe, G.: Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12(01), 2825–2830 (2012)
Quinlan, J.R.: Induction of decision trees. Mach. Learn. 1(1), 81–106 (1986)
Rumelhart, D.E., Hinton, G.E., Williams, R.J.: Learning representations by back-propagating errors. Nature 323(6088), 533 (1986)
Ryzhov, A.E., Grigoriev, B.A., Orlov, D.M.: Improving fluid filtration to saline reservoir rocks. In: Book of Abstracts of International Gas Union Research Conference (IGRC-2014) (2014)
Schmidhuber, J.: Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015)
Soulaine, C., Tchelepi, H.A.: Micro-continuum approach for pore-scale simulation of subsurface processes. Transp. Porous Media 113(3), 431–456 (2016)
Stewart, G.: Well Test Design and Analysis. PennWell, Tulsa (2011)
Tahmasebi, P., Sahimi, M., Shirangi, M.G.: Rapid learning-based and geologically consistent history matching. Transp. Porous Media 122(2), 279–304 (2018)
Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 58(1), 267–288 (1996)
Unsal, E., Dane, J., Dozier, G.V.: A genetic algorithm for predicting pore geometry based on air permeability measurements. Vadose Zone J. 4(2), 389–397 (2005)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Erofeev, A., Orlov, D., Ryzhov, A. et al. Prediction of Porosity and Permeability Alteration Based on Machine Learning Algorithms. Transp Porous Med 128, 677–700 (2019). https://doi.org/10.1007/s11242-019-01265-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-019-01265-3