Ion-Exchange Inverse Problem for Low-Salinity Coreflooding

Abstract

The data input for reservoir simulation of low-salinity waterflood in sandstones includes adsorption isotherms, or equilibrium constants for all cation-exchange reactions, and cation-exchange capacity (CEC). We develop a novel method for determination of those functions from the laboratory data of low-salinity coreflooding; the inverse problem is solved; rather, matching is applied. Changing independent time variable to Lagrangian coordinate transforms the governing system for two-phase multicomponent flow into a single-phase system of mass balance equations for each ion and the volumetric balance equation for water. It allows determining the adsorption isotherms for all ions, or equilibrium constants and CEC, from the breakthrough ion concentrations, using the exact solution of ion-exchange inverse problem. Further, the fractional flow and relative permeability can be determined from the effluent water cut and pressure drop histories, using the Welge’s and JBN methods; here each data point corresponds to the breakthrough values of ion concentrations. We show that for four-ion waterflooding, only two constants from two equilibrium constants and CEC can be determined. Treatment of five coreflood data sets shows a close agreement between the laboratory data and the results of inverse problem solution.

Appendices

Appendix A: Reformulation of the Welge’s and JBN Methods in Invariant Terms

In this appendix, we derive the solution for two inverse problems for “normal” waterflood, where c = const in Eq. (1), i.e. we reproduce the classical Welge and JBN methods in the form, which is used in the text (Welge 1952; Johnson et al. 1959; Jones and Roszelle 1978). The Welge’s method determines fractional flow function f(s) from the breakthrough water cut f(1, t_D) (Fig. 2). The JBN method determines total mobility Λ(s) from the pressure drop across the core Δp(t_D).

The derivation is based on Green’s theorem: the following double integral over the plane region Δ bounded by a simple closed curve ∂Δ is equal to the line integral around the curve ∂Δ (Polyanin and Manzhirov 2006)

$$ \iint\limits_{\Delta } {\left( {\frac{\partial s}{{\partial t_{\text{D}} }} + \frac{\partial f}{{\partial x_{\text{D}} }}} \right){\text{d}}x_{\text{D}} {\text{d}}t_{\text{D}} = \oint\limits_{\partial \vartriangle } {f{\text{d}}t_{\text{D}} - s{\text{d}}x_{\text{D}} } } $$

(A-1)

Integrate both sides of Eq. (1) with c = const over the inner of triangle Δ: (0, 0) → (1, 0) → (1, t_D) → (0, 0) in plane (x_D, t_D) (Fig. 3c). As it follows from Green’s theorem (A-1),

$$ \oint\limits_{\partial \vartriangle } {f{\text{d}}t_{\text{D}} - s{\text{d}}x_{\text{D}} } = 0 $$

(A-2)

Calculation of contour integral (A-1) over each side of the triangle (0, 0) → (1, 0), (1, 0) → (1, t_D), and (0, 0) → (1, t_D) accounting for initial and boundary conditions yields:

$$ - s^{I} ;\;\int\limits_{0}^{t} {f\left( {1,u} \right)} {\text{d}}u;\;f\left( {1,t_{\text{D}} } \right)t_{\text{D}} - s\left( {1,t_{\text{D}} } \right), $$

(A-3)

respectively. Substituting three obtained integrals (A-3) into Eq. (A-1) results in

$$ s\left( {1,t_{\text{D}} } \right) = s^{I} + \int\limits_{0}^{{t_{\text{D}} }} {\left[ {f\left( {1,t_{\text{D}} } \right) - f\left( {1,y} \right)} \right]} {\text{d}}y $$

(A-4)

Corresponding values f(1, t_D) and s(1, t_D), as calculated by Eq. (A-3), define a parametric curve f = f(s). Usually, a number of moments t_Dk, k = 1, 2… K, are set, water cut values f(1, t_Dk) are measured at the corresponding moments, and s(1, t_Dk) are calculated using Eq. (A-3). It yields the fractional flow curve (s_k, f_k) as determined in K points.

JBN’s formula for total mobility is obtained by expressing the pressure gradient from Eq. (3) for c = const, integrating in x_D from zero to one, changing the integration variable from x_D to ξ = 1/t_D and taking derivation over 1/t_D from both sides of the obtained equality:

$$ \varLambda^{ - 1} \left( {s,\vec{c}} \right) = \frac{\text{d}}{{{\text{d}}y}}\left| {\begin{array}{*{20}c} {} \\ {y = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {t_{\text{D}} }$}}} \\ \end{array} } \right.\left( {\Delta p\left( y \right)y} \right) $$

(A-5)

where saturation in left-hand side of Eq. (A-4) corresponds to the outlet x_D = 1 at the moment t_D.

The above derivations have been performed using just the fact of self-similarity of the direct solution (1) that results in constant saturation along straight lines x_D/t_D = const. The inverse solutions given by Eqs. (A-3) and (A-4) are independent of the direct solution itself, and the Buckley–Leverett formulae have not been used during the derivations.

Appendix B: Riemann Solution for Single-Phase Ion-Exchange Flow

Following Pope et al. (1978) and Venkatraman et al. (2014), here we present the Riemann solution for system (22–24) subject to initial and boundary conditions (25, 26) for one-phase three-component flow with concentration alteration injection. General methods for Riemann solutions of conservation law systems can be found from Gelfand (1959), Courant and Friedrichs (1999), and Polyanin and Manzhirov (2006).

Equation (24) separates from the rest of system (22, 23). Solution of Eq. (24) subject to initial and boundary conditions (25, 26) in self-similar form is:

$$ c_{4} \left( {x_{\text{D}} ,\varphi } \right) = \left\{ {\begin{array}{*{20}c} {c_{4}^{\text{J}} ,} & {\varphi > 0} \\ {c_{4}^{\text{I}} ,} & { - s^{\text{I}} x_{\text{D}} < \varphi < 0} \\ \end{array} } \right. $$

(B-1)

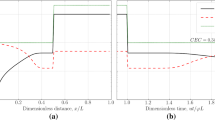
Sorption of Ca and Mg cations yields deceleration of their concentration fronts if compared with the front of the traced water. On the contrary, Cl anion does not adsorb, so the speed of Cl front coincides with the speed of traced water front. Therefore, in (x_D, t_D) plane, where concentrations of Ca and Mg differ from there initial values, c₄ = c ^J₄ (Fig. 5). Substitution of c₄ = c ^J₄ into 3 × 3 system (22–24) allows for its degeneration into 2 × 2 system (22, 23). The boundary conditions for c₂ and c₃ remain (26). Let us find the initial conditions.

Mass balance equations for shocks in system (22–24) are

$$ \left[ {a_{2} \left( {c_{2} ,c_{3} ,c_{4} } \right)} \right]V = \left[ {c_{2} } \right] $$

(B-2)

$$ \left[ {a_{3} \left( {c_{2} ,c_{3} ,c_{4} } \right)} \right]V = \left[ {c_{3} } \right] $$

(B-3)

$$ 0 \times V = \left[ {c_{4} } \right] $$

(B-4)

where the jump of physics parameter A is the difference between A values ahead and behind the shock: [A] = A⁺− A⁻, and V is the shock speed at (x_D, φ) coordinate.

Consider shock at φ = 0. Its speed is infinite. So, the solution (B-1) fulfils mass balance equation for chloride. The fast chloride front I → P, which is an indifferent step wave, has a constant speed equal to one in (x_D, t_D)-plane and infinity in (x_D, φ)-coordinates. Tending V to infinity in Eqs. (B-2, B-3) yields the following conditions on the shock I → P with trajectory φ = 0:

$$ \left[ {a_{2} \left( {c_{2} ,c_{3} ,c_{4} } \right)} \right] = \left[ {a_{3} \left( {c_{2} ,c_{3} ,c_{4} } \right)} \right] = 0 $$

(B-5)

The corresponding point behind the front φ = 0 in concentration space is denoted as P (Figs. 4, 5, 6). Two Eqs. (B-5) determine concentrations c ^P₂ and c ^P₃ behind the c₄-shock. Geometrically, it corresponds to horizontal straight lines P–I for sorption curves of Ca and Mg (Fig. 4a, b, respectively). Now the initial data are transferred from the straight line φ = − s^Ix_D, point I to straight line φ = 0, point P. This allows transforming the 3 × 3 Riemann problem (22–26) to the 2 × 2 Riemann problem (22, 23) for decay of discontinuity J → P.

Mass balance equations (B-5) determine the concentrations behind the front φ = 0:

$$ c_{2}^{\text{P}} = c_{2}^{\text{I}} \frac{{ - 1 + \sqrt {1 + 4\left( {\frac{{c_{3}^{\text{I}} + c_{2}^{\text{I}} }}{{c_{1}^{I2} }}} \right)c_{4}^{\text{J}} } }}{{2\left( {c_{3}^{\text{I}} + c_{2}^{\text{I}} } \right)}};\quad c_{3}^{\text{P}} = c_{3}^{\text{I}} \frac{{ - 1 + \sqrt {1 + 4\left( {\frac{{c_{3}^{\text{I}} + c_{2}^{\text{I}} }}{{c_{1}^{{{\text{I}}2}} }}} \right)c_{4}^{\text{J}} } }}{{2\left( {c_{3}^{\text{I}} + c_{2}^{\text{I}} } \right)}} $$

(B-6)

as shown in Fig. 6. According to mass balance conditions (B-5), points P and I are located on the same horizontal straight line (Fig. 4a, b).

Solution of 2 × 2 Riemann problem (22, 23) may consist of two rarefaction and two shock waves. Velocities of rarefaction and shock waves for system (22, 23) are positive, so the solution is compatible with c₄ = c ^J₄ in solution (B-1).

Eigenvalues of system (22, 23) λ_i, i = 2, 3 are:

$$ \lambda_{2} \left( {c_{2} ,c_{3} } \right) = \frac{{a_{33} + a_{22} - \sqrt {\left( {a_{33} - a_{22} } \right)^{2} + 4a_{32} a_{23} } }}{2},\quad a_{ij} = \frac{{\partial a_{i} \left( {c_{2} ,c_{3} ,c_{4}^{\text{J}} } \right)}}{{\partial c_{j} }} $$

(B-7)

$$ \lambda_{3} \left( {c_{2} ,c_{3} } \right) = \frac{{a_{33} + a_{22} + \sqrt {\left( {a_{33} - a_{22} } \right)^{2} + 4a_{32} a_{23} } }}{2} $$

(B-8)

The explicit expressions for first-order partial derivatives are calculated from Eqs. (B-7, B-8); they are cumbersome and are not presented in the text. However, Helfferich and Klein (1970) proves that eigenvalues of matrix a_ij are positive. Speeds of c₂- and c₃-shocks are positive too. Therefore, the solution ahead of the anion shock for − s^Ix_D ≤ φ < 0 is constant and equal to initial values. Behind the shock for φ > 0, chloride concentration is constant, so the continuous solutions of 3 × 3 system (22–24) are described by 2 × 2 system (22, 23) with c₄ = c ^J₄ .

Eigenvectors form two vector fields in (c₂, c₃)-space, denoted as R₂ and R₃ (Figs. 6, 7). Choosing c₂ as an independent parameter along trajectories yields a system of two ordinary differential equations for λ₂ and λ₃

$$ \frac{{{\text{d}}c_{3} }}{{{\text{d}}c_{2} }} = \frac{{a_{32} }}{{\lambda_{k} - a_{33} }},\quad k = 2,3 $$

(B-9)

Rarefaction waves (B-7, B-8) for k = 2 and 3 are called the R₂ and R₃ waves, respectively.

For any shock with finite speed, it follows from Eqs. (B-2–B-4) that

$$ V^{ - 1} = \frac{{{\text{d}}\varphi }}{{{\text{d}}x}} = \frac{{\left[ {a_{3} } \right]}}{{\left[ {c_{3} } \right]}} = \frac{{\left[ {a_{2} } \right]}}{{\left[ {c_{2} } \right]}} $$

(B-10)

Now we need to connect points J and P by a sequence of rarefaction and shock waves, given by Eqs. (B-9, B-10), respectively. These are shown in Fig. 7. The blue curve shows rarefaction R₃ corresponding to eigenvalue (B-7), and black curves show rarefactions R₂ corresponding to eigenvalues (B-8), i.e. R₂ is a slow wave, and R₃ is a fast wave. The figure also shows so-called shock loci marked by arrows; each point of the curves fulfils the mass balance conditions (B-10) with point P, i.e. a jump to the point P obeys the condition (B-10). Two families of shocks S₂ and S₃ correspond to two roots of transcendental equations (B-10); here S₂ corresponds to slow shocks and S₃ to fast shocks. In each point of phase plane (c₂, c₃), S₂-shock locus tangents rarefaction R₂, and S₃-shock locus tangents rarefaction R₃.

Shocks in Fig. 7 fulfil the Lax and Oleinik stability conditions (Bedrikovetsky 1993).