1 Introduction

Studying the transport parameters of rocks in deep underground structures is required for geological disposal and/or reservoir engineering applications. Cases in point are measures to hinder the migration of radioactive waste from geological repositories to the biosphere and storing CO2 in porous subsurface formations. Accordingly, subsurface rock formations are of interest to rock mechanics experts as they can potentially be viable sites for the development of underground structures.

Several studies have indicated that anisotropy in the pore structure and intermittent connectivity cause anisotropy in the domain’s permeability and diffusivity. In sandstone, for instance, the permeability in the direction parallel to the bedding is controlled by the highly permeable clay-free layers while the permeability in the direction normal to the bedding is determined by the shale content of the less permeable silty layers (Clavaud et al. 2008). Farver and Yund (1999) reported that the diffusion coefficient of oxygen in the direction parallel to foliation for a mica-bearing rock is approximately 2–10 times greater than that in the direction normal to the bedding. The diffusivity of clay samples after compaction has also been observed to be much higher in the direction parallel to the fabric than that normal to the fabric because of the lower tortuosity (Van Loon et al. 2004). Wan et al. (2015) demonstrated the same relation between the pore structure and diffusivity anisotropy of a single cubic shale sample by eliminating the impact of the samples’ heterogeneity on the results. Yokoyama and Nakashima (2005) reported that the diffusion coefficients of pore water K+ ions in rhyolite were 5–6 and 7–9 times smaller in the direction normal to the flow plane than the other orthogonal and parallel orientations. Because the nuclides dissolved in water travel easily through the sufficiently large pore spaces in sandstone, advective flow takes on a significant role in their migration through groundwater. However, the advective flow is impeded by small pores or pore throat sizes, such as those in mudstone and shale. Consequently, diffusion becomes a relatively dominant phenomenon for nuclide migration through these materials. To determine the migration of substances such as dissolved nuclides and CO2 that depend on the flow state of groundwater, the anisotropic ratios for both the permeability and diffusivity are required. However, it is still unclear whether a transport parameter for either the permeability or diffusivity is applicable to the other.

In this study, both experimental procedure and numerical modeling were employed to examine the effects of the pore structure on the anisotropy of transport parameters for Berea sandstone, whose grain arrangement is dominated by sedimentation. To estimate the permeability and diffusion parameters, this work focused on the phenomena separately. Permeability and diffusivity experiments were performed on a single rock sample in sequence under an isotropic confining pressure. The experimental results indicated the anisotropy ratios for the permeability and diffusivity of Berea sandstone. To reveal the cause of the difference in anisotropy ratios, a numerical analysis was performed by using the pore geometry. The pore structure of Berea sandstone was examined with 3-D X-ray computed tomography (CT) to investigate the influence of the porosity, tortuosity, and constrictivity on the permeability and diffusivity of Berea sandstone. The diffusivity of the sample was calculated from the CT data, and its permeability was estimated with the lattice Boltzmann method (LBM). In computational fluid dynamics, LBM is a parallel and efficient algorithm that serves as a substitute for the Navier–Stokes equations (Benzi et al. 1992). LBM has been employed in various fields, including earth sciences and geology, to understand transport in open pores and porous structures. For example, it was used by Auzerais et al. (1996) to examine the scale dependence and influence of heterogeneities of transport properties in Fontainebleau sandstone; by Okabe and Blunt (2004) to predict the permeability of porous media based on 3-D CT images and reconstructed 2-D images; by Gao et al. (2015) to study the permeability of sandstones for the voxel size dependency; and by Genty et al. (2017) to study the micro-fracture of indurated argillite Oparinus clay and obtain the effective diffusion coefficient. Finally, the experimental and numerical results were compared to explore the relationship between the anisotropic transport parameters and bedding plane direction.

2 Materials and Methods

2.1 Specimen Description

Berea sandstone has long been used as the de facto standard material in laboratory experiments for rock mechanics and reservoir engineering applications, such as radioactive waste disposal, CO2 storage, or petroleum engineering practices. For permeability and diffusivity tests, disk-shaped rock samples with a diameter of 50 mm and thickness of 10 mm were extracted in two orthogonal directions from a block, with the Z direction being normal to the bedding plane and the X and Y directions being parallel to that (Fig. 1). The Berea sandstone used in the study was comprised of predominantly well-sorted and well-rounded quartz grains with minor amounts of feldspar and opaque minerals (Fig. 2). The bedding was easily visible and consisted of opaque minerals (iron sand and minor amounts of zircon). The porosity of the bedding bands is about lower than that of the other parts of the sandstone, and this was observed using X-ray CT data, as described in Sect. 3.2. The characteristic lamination showed that the Berea sandstone was deposited as beach sediments (Fujii et al. 2015). The porosity, pore structure, and average pore radius of the samples were characterized by mercury intrusion porosimetry using a Micrometrics AutoPore IV 9520 to determine the pore size distribution from 2 to 500 µm (Fig. 3). The Berea sandstone had unimodal characteristics at 5–10 µm, and small pores were present up to 5 nm. The porosity was 18.29%.

Fig. 1
figure 1

Berea sandstone for the permeability and diffusivity tests cored in the direction parallel to the bedding

Full size image
Fig. 2
figure 2

Thin section of Berea sandstone. Qt quartz, Fl feldspar, Op opaque minerals

Full size image
Fig. 3
figure 3

Total porosity and pore size distribution of Berea sandstone with the mercury intrusion porosimeter

Full size image

2.2 Permeability Experiment

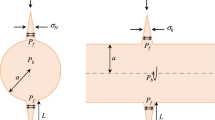
The experimental system presented by Takeda et al. (2014) was employed to perform permeability and diffusivity experiments on a rock sample (Fig. 4). Prior to the permeability experiments, a rock sample was jacketed with a neoprene rubber and placed in the pressure vessel. The sample was immersed in a 0.1 M NaCl solution, which was used as the permeant fluid. The experiments were performed with the constant head method at a hydraulic head difference of 3 kPa and a confining pressure of 500 kPa (ASTM 2006) at room temperature (25 °C). The cumulative change in the effluent solution was measured by using an electric balance. The hydraulic conductivity K (m/s) for the constant head experiment was obtained using Darcy’s law:

$$ K = \frac{qL}{AH} $$
(1)

where q is the discharge (m3/s), L is the sample length (m), A is the cross-sectional area of the specimen (m2), and H is the constant head pressure (m). The hydraulic conductivity can be converted into the intrinsic permeability k (m2) as follows:

$$ k = \frac{\eta }{\rho g}K $$
(2)

where ρ and η are the fluid density (kg/m3) and fluid viscosity (Pa s), respectively, and g is the gravitational acceleration (m/s2). The permeability experiments were conducted at room temperature (25 °C), and ρ and η were 1.036 × 103 kg/m3 and 9.6 × 10−4 Pa s, respectively.

Fig. 4
figure 4

Diagram for measuring the permeability and diffusivity of the sample

Full size image

2.3 Diffusion Experiment

Diffusivity experiments were performed on each sample with the through-diffusion method at a concentration difference of 0.6–0.1 M NaCl and a confining pressure of 500 kPa. The temperature was controlled at 40 °C by using a heating system. This temperature was selected because it is difficult to keep the room temperature constant for 1 month as the air conditioner introduces errors of ± 1.5 °C. The reservoir solution was circulated by magnetic gear pumps to keep the solute concentration uniform in the reservoirs. The effective diffusion De can be calculated as follows (Wolfrum et al. 1988):

$$ \ln \left( {\frac{\Delta C}{{\Delta C_{0} }}} \right) = - \frac{{A \cdot D_{\text{e}} }}{L} \cdot \left( {\frac{1}{{V_{\rm d} }} + \frac{1}{{V_{\rm u} }}} \right) \cdot t $$
(3)

where ΔC and ΔC0 are the concentration differences between the upstream and downstream reservoirs at time t and the initial concentration difference, respectively, and Vu and Vd correspondingly represent the upstream and downstream volumes of the reservoir. The temperature of the incubator was set to 40 °C for all tests.

2.4 CT System for Micro-focus X-rays

The 3-D geometry of Berea sandstone was captured using micro-focus X-ray CT with the lattice Boltzmann method to determine the permeability and diffusivity in the simulations. High-resolution X-ray CT was performed on a drilled cylindrical core with a diameter of 10 mm. Each voxel of this 3-D image had a linear dimension of 5 µm. The size of the reconstructed 3-D image for the cube was 3003 voxels (1.5 × 1.5 × 1.5 mm3), and this included one of the sequential beddings on the X–Y plane in the representative specimen. The cube of 3003 voxels represents the limit size of the LBM simulation by a standard computer (Intel core i7 CPU x980 3.3 GHz (12 CPUs), 48 GB RAM). In general, CT images of porous media are gray scale and have a bimodal population: One mode corresponds to the signal from the pore space, and the other corresponds to that of the grain. We used the porosity from the results of the mercury intrusion porosimetry to binarize the samples into pore space and grain segments. The Kriging-based algorithm developed by Linquist and Venkatarangen (1999) was used to binarize the voxel images. By distinguishing the pore throat as a local minimum of the boundary sectional area for the pores (Fig. 5), data on the pore structure, spatial distribution for the pore and pore throat sizes, tortuosity, and porosity distribution were derived. The minimum pore throat size is 5 µm, which is restricted owing to the CT resolution. The medial axes of the pore structure were also obtained by using the burn algorithm (Linquist et al. 1996) and can be used to calculate the shortest paths and tortuosity from one end face to the opposite side (Fig. 5).

Fig. 5
figure 5

Schematic of tortuosity of the porous matrix. The medial axis, shown in yellow, was obtained by applying the burn algorithm to the CT image

Full size image

2.5 Diffusion Modeling

According to Van Brakel and Heertjes (1974), the effective diffusion coefficient (De) can be described in terms of the porosity (φ), geometric constrictivity (δg), tortuosity (τ), and tracer diffusivity in bulk liquid water, Dw (m2 s−1):

$$ D_{\text{e}} = \varphi \frac{{\delta_{\text{g}} }}{{\tau^{2} }}D_{\text{w}} $$
(4)

The tortuosity is defined by

$$ \tau = l/l_{0} $$
(5)

where l0 is the apparent length of the element and l is the length of the fluid flow path through the porous matrix (Fig. 5). As the tortuosity increases, the porous matrix becomes more complicated. When the fluid flow in a porous matrix is being considered, the tortuosity becomes meaningful for permeability. The constrictivity is generally the ratio of the radius of the diffusing particle to the pore radius; hence, it is a dimensionless parameter between 0 and 1. Takahashi et al. (2009) gave the following relation for the geometric constrictivity δg :

$$ \delta_{\text{g}} = \frac{{\left( {{\text{maximum }} \times {\text{minimum\;cross-section}}} \right)^{{\frac{1}{2}}} }}{{{\text{mean\;cross\;section}}}} = \frac{{\left( {\pi r_{\rm p}^{2} \times \pi r_{\rm t}^{2} } \right)^{{\frac{1}{2}}} }}{{\left( {\frac{{\pi r_{\rm p}^{2} + \pi r_{\rm t}^{2} }}{2}} \right)}} $$
(6)

where rp and rt are assumed to be the approximation radii of the pore and throat, respectively. In this study, rp and rt were derived from burn algorithm applied to the 3-D CT pore volume. \( \delta_{\text{g}}^{||} \) and \( \delta_{\text{g}}^{ \bot } \) denote the average value of δg through all shortest paths parallel and normal to the bedding plane.

2.6 Flow Simulation with the Lattice Boltzmann Method (LBM)

In the LBM, the evolution of the particle distribution function fa (x, t) at point x and time t with velocity ea is computed as follows (Chen and Doolen 1998):

$$ \frac{{\partial f_{a} }}{\partial t} = - \varvec{e}_{a} \cdot \nabla f_{a} + \varOmega_{a} \left( {\varvec{x},t} \right) $$
(7)
$$ \varOmega_{a} \left( {\varvec{x},t} \right) = - \frac{1}{{\tau_{f} }}\left[ {f_{a} \left( {\varvec{x},t} \right) - f_{a}^{\text{eq}} \left( {\varvec{x},t} \right)} \right] $$
(8)

where f eq a is an equilibrium distribution function, τf is a single relaxation time, and t is a time step during which the particle travels the lattice spacing. The Bhatnagar–Gross–Krook (BGK) model is used for the collision term Ωa (x, t) in Eq. (7). According to the kinetic theory of fluids, the density ρ and flow velocity u under a constant temperature can be defined in terms of the particle distribution function (Chen and Doolen 1998; Misawa et al. 2004):

$$ \rho = \mathop \sum \limits_{a} f_{a} = \mathop \sum \limits_{a} f_{a}^{\text{eq}} $$
(9)
$$ \rho \varvec{u} = \mathop \sum \limits_{a} f_{a} \varvec{e}_{a} = \mathop \sum \limits_{a} f_{a}^{\text{eq}} \varvec{e}_{a} $$
(10)

The D3Q15 model (Inamuro et al. 1999) for the particle velocity set was used in the following calculations. The Navier–Stokes equations have second-order nonlinearity. The general form of the equilibrium distribution function up to the second-order term can be written as (Chen and Doolen 1998)

$$ f_{a}^{\text{eq}} = w_{a} \rho \left[ {1 + \frac{{\varvec{e}_{\varvec{a}} \cdot \varvec{u}}}{{c_{s}^{2} }} + \frac{{\left( {\varvec{e}_{\varvec{a}} \cdot \varvec{u}} \right)^{2} }}{{2c_{s}^{4} }} - \frac{{\varvec{u} \cdot \varvec{u}}}{{2c_{s}^{2} }}} \right] $$
(11)

where wa = 2/9 (a = 0), 1/9 (a = 1–6), and 1/72 (a = 7–14). This expansion is valid only for small velocities or small Mach numbers \( \left| \varvec{u} \right| \)/cs, where cs is the speed of sound. Equation (11) is applicable for flow with low compressibility. In the case of an incompressible flow (ρ0 is constant), f eq a is derived as follows (He and Luo 1997, Onishi et al. 2001):

$$ f_{a}^{\text{eq}} = w_{a} \left[ {\frac{p}{{c_{s}^{2} }} + \rho_{0} \left\{ {\frac{{\varvec{e}_{\varvec{a}} \cdot \varvec{u}}}{{c_{s}^{2} }} + \frac{{\left( {\varvec{e}_{\varvec{a}} \cdot \varvec{u}} \right)^{2} }}{{2c_{s}^{4} }} - \frac{{\varvec{u} \cdot \varvec{u}}}{{2c_{s}^{2} }}} \right\}} \right] $$
(12)

where p is the pressure and cs = \( 1/\sqrt 3 \). The pressure and flow velocity are defined as follows:

$$ p = \mathop \sum \limits_{a} f_{a} c_{s}^{2} = \mathop \sum \limits_{a} f_{a}^{\text{eq}} c_{s}^{2} $$
(13)
$$ \rho_{0} \varvec{u} = \mathop \sum \limits_{a} f_{a} \varvec{e}_{a} = \mathop \sum \limits_{a} f_{a}^{\text{eq}} \varvec{e}_{a} $$
(14)

Equations (7) and (8) can be discretized into the semi-Lagrangian form with second-order accuracies in both space and time as follows:

$$ f_{a} \left( {\varvec{x} + \varvec{e}_{a} \Delta t,t} \right) = f_{a} \left( {\varvec{x},t} \right) - \frac{\Delta t}{{\tau_{f} }}\left[ {f_{a} \left( {\varvec{x},t} \right) - f_{a}^{\text{eq}} \left( {\varvec{x},t} \right)} \right] $$
(15)

where Δt is a constant increase in time and x + eaΔt denotes the position of the neighboring x in the direction of the velocity ea. The kinematic viscosity ν is defined by

$$ \nu = c_{s}^{2} \left( {\tau_{f} - \frac{\Delta t}{2}} \right) $$
(16)

The Reynolds number is a primary dimensionless parameter for the behavior of all Newtonian fluids and is given by the ratio of the inertia and viscous forces:

$$ Re = \frac{LU}{\nu } $$
(17)

where U and L are the characteristic velocity and length scales of the flow, respectively. Here, the differential fluid pressure Δpreal in real dimensions can be calculated as follows:

$$ \Delta p_{\text{real}} = \frac{{\left( {\rho_{0} U^{2} } \right)_{\text{real}} }}{{\rho_{0} U^{2} }}\Delta p $$
(18)

The intrinsic permeability from LBM can be calculated by using Δpreal and the discharge from Eqs. (1), (2), and (18).

To compare the experimental results and LBM simulation, the appropriate parameters needed to be determined. The CT images had 3003 voxels with a 5 µm resolution. The calculation area of LBM was 3003 lattice cells on a Cartesian axis with lattice spacings of Δx = Δy = Δz = 1. The incremental increase in time Δt was set to 1.0 for the calculation procedure. The simulations were run at Re = 2 to be close to the experimental differential head, and additional analysis was performed at Re = 0.1. The boundary conditions for fa of the moving particles were set as follows: For nonslip solid lattice cells, a bounce-back condition was applied to the particles moving with ea from the fluid side to the solid side. These particles returned to the fluid side in the opposite direction of − ea. On the inflow and outflow boundaries, the particles coming into the calculation area from the outside were assumed to be in local equilibrium state according to the outside pressure and fluid velocity.

3 Results

3.1 Experimental Results

Equations (1) and (2) were used to calculate the intrinsic permeability in the directions normal and parallel to the bedding (Fig. 6). The permeability experiments were conducted three times for each direction. The average intrinsic permeability in the direction normal to the bedding (k⊥) was 1.03 × 10−14 m2, while it was 8.76 × 10−14 m2 in the parallel direction (k‖). Figure 7 shows the results of the diffusivity experiments. The effective diffusion coefficient for NaCl was calculated from its linear relationship with ln(ΔC/ΔC0), as given in Eq. (3). The effective diffusion coefficient in the directions parallel (D ‖e ) and normal (D ⊥e ) to the bedding was 4.84 × 10−11 and 3.49 × 10−11 m2/s, respectively. The anisotropy ratios for the intrinsic permeability and diffusion coefficient (i.e., k‖⁄k⊥ and D ‖e ⁄ D ⊥e ) were estimated to be 8.50 and 1.39, respectively. Table 1 presents the results obtained via the experimental procedure and LBM modeling (described in the subsequent sections). The difference in the anisotropy ratios suggests that a pore structure with a preferential orientation affects anisotropies of the permeability and diffusivity differently.

Fig. 6
figure 6

Amount of for specimens in the constant pressure permeability experiment. The experiment was conducted three times, and the results were averaged to determine the permeability in each direction

Full size image
Fig. 7
figure 7

Results of the diffusivity test. The NaCl concentrations of the reservoir solutions were measured in the directions a parallel and b perpendicular to the bedding

Full size image
Table 1 Permeability and diffusivity values obtained by experimental results and models
Full size table

3.2 CT Analysis

Figure 8a shows the CT pore volume data of Berea sandstone for a volume of 1.5 mm3 (3003 voxels). Figure 8b–d shows 2-D image cross sections in the X, Y, and Z directions. The bulk density of the bedding was higher than that outside the bedding. Therefore, the bedding showed that the pores were less interconnected in the bedding plane. Kim et al. (2016) compared the porosity inside and outside the bedding of the Berea sandstone by using micro-focus X-ray CT. They observed that the zone outside the bedding has more pores than the zone inside the bedding and that the pores are more interconnected in the zone outside the bedding.

Fig. 8
figure 8

Pore structure of Berea sandstone (1.5 mm × 1.5 mm × 1.5 mm). a The light and dark areas correspond to grain and pore spaces, respectively. b–d The light and dark areas correspond to pore spaces and grain, respectively

Full size image

The tortuosity from one end face to the opposite side can be calculated from the medial axis (Fig. 5) of the 3-D CT image using Eq. (5). Figure 9 shows the tortuosity distribution in three directions. The tortuosity was greatest in the Z direction.

Fig. 9
figure 9

Tortuosity distribution in three directions. The X–X′ and Y–Y′ directions are parallel to the bedding, and the Z–Z′ direction is normal to the bedding

Full size image

Figure 10 depicts the cross-sectional porosity change along the perpendicular (Z) and parallel (Y) directions to the bedding with pressure distribution from the LBM results. The Berea sandstone exhibited significant cross-sectional porosity changes in the Z direction. The cross-sectional porosity was at its minimum of 7.87% at a distance of 0.6 mm from the end surface; however, it increased to 27.58% where the section passed through narrow pore spaces. In the Y direction, however, the cross-sectional porosity was relatively consistent with the minimum and maximum cross-sectional porosities being 14.10% and 23.52%, respectively. This directional anisotropic trend confirmed the characteristic pore geometry due to beach sedimentation (Fig. 2).

Fig. 10
figure 10

Cross-sectional porosity of the sample in the directions parallel (Y–Y′) and normal (Z–Z′) to the bedding plane

Full size image

The model results for the median tortuosity (τ‖ = 1.8 and τ⊥ = 1.95), constrictivity (δ ‖g  = 0.761 and δ ⊥g  = 0.757), porosity (φ = 18.29%), and tracer diffusivity in bulk liquid water (Dw = 2.015 × 10−9 m2/s) were used in Eq. (4) to obtain the effective diffusivities in two perpendicular directions. The results for the parallel and normal directions to the bedding plane were 8.63 × 10−11 and 7.35 × 10−11 m2/s, respectively, which are slightly higher than those obtained via the experimental procedure. The model of the diffusivity anisotropy is affected by tortuosity anisotropy in the case of using Eq. (4).

3.3 LBM Results

The LBM results for the steady-state flow after 500,000 time steps are presented here. The differential pressure calculated from Eq. (18) was 4.5 kPa, which is sufficiently close to the experimental condition (3.0 kPa). Figure 10 shows the relation between the cross-sectional porosity and pressure distribution in the directions parallel and normal to the bedding. The pressure distribution in the normal direction to the bedding showed a sudden decrease at low-porosity areas. Figure 11 shows the typical fluid pressure distribution of the LBM flow in the direction parallel to the bedding (Y–Y′). The fluid pressure gradually decreased with distance from the inflow boundary.

Fig. 11
figure 11

Fluid pressure distribution of the LBM flow from the X–Z plane

Full size image

Figure 12 depicts a representative section cut from the 3-D LBM simulation results. The rock pores are not connected in the 2-D image because the pore structure is very intricate. Figures 12b–f is acquired using the maximum intensity projection, which enabled the maximum flow velocity and/or fluid pressure to be illustrated as 2-D front view figures for a 0.15 mm (30 pixels) thick plate containing 3-D pore structures. The bedding with the minimum cross-sectional porosity in the Z direction was at 0.6 mm from the bottom. The flow velocity in the Y direction was relatively uniform (Fig. 12c). The pressure distribution in the Y direction (Fig. 12d) showed that the pressure gradually decreased with distance from the inflow boundary. On the other hand, a high flow rate at low-porosity areas was noted in the Z direction (Fig. 12e). The pressure distribution results in the Z direction (Fig. 12f) showed a sudden decrease at low-porosity areas, for which the numeric data are shown in Fig. 10b. Hence, the advection flow is restricted by a bottleneck effect resulting from low cross-sectional porosity in the direction normal to the bedding.

Fig. 12
figure 12

LBM results: a pore structure taken from X-ray CT, b pore structure cut from the 3D pore structure with a 0.15 mm thickness. Platen figures cut from the 3D LBM results applied to the cubic figure: flow velocity and pressure distribution of the pore structure for the directions c, d parallel to the bedding and e, f normal to the bedding as shown by the maximum intensity projection

Full size image

The steady-state intrinsic permeabilities in the Z (\( k_{\text{LBM}}^{ \bot } \)) and Y (\( k_{\text{LBM}}^{||} \)) directions were 5.01 × 10−14 and 4.26 × 10−13 m2, respectively. The anisotropy ratio of the permeability (\( k_{\text{LBM}}^{||} /k_{\text{LBM}}^{ \bot } \)) was 8.50.

4 Discussion

4.1 Diffusivity Anisotropy Due to the Pore Structure in the Bedding

In this study, the experimental diffusivities were acquired as D ‖e  = 4.84 × 10−11 m2/s and D ⊥e  = 3.49 × 10−11 m2/s. For reference, the diffusivity of Cl- in Berea sandstone is 1.03 × 10−10 m2/s (Yokoyama and Nakashima 2005), which is approximately the same as the value calculated from the CT data. The relatively low diffusivities in the normal direction to the bedding have been reported in many other studies. Consequently, the results of this study confirm the diffusivity anisotropy due to anisotropic pore structures in the bedding.

One possible reason for the difference between the calculated and experimental results is the overestimation of the pore size. When binarization is carried out according to the porosity, the volume of nanopores with radii of under 5 µm is replaced with that of pores having radii of over 5 µm, which extends the pore structure. Further high-resolution analyses and/or the application of additional simulation for the diffusivity are required to arrive at a more detailed explanation.

4.2 Permeability Anisotropy Due to the Bedding Plane

The permeability was also higher in the parallel direction to the bedding than in the normal direction. In addition, the permeabilities from the LBM simulation were higher than the corresponding experimental values, which may stem from the resolution problem. However, Peng et al. (2014) showed two micro-focus CT images of Berea sandstone that were binarized using the Kriging method with resolutions of 1.85 and 5.92 µm/voxel, which returned nearly identical permeabilities. This indicates that 5.92 µm is a sufficiently high resolution to capture the main flow paths for this rock and that smaller pores need not always be resolved. The permeability ratios in the directions perpendicular and parallel to the bedding were almost the same as those in the experimental results. Thus, the LBM simulation is considered to be applicable for evaluating the permeability anisotropy.

The permeability experiment was conducted at a differential pressure of 3 kPa. Because Berea sandstone has high permeability, the flow rate through the specimen was probably fast enough to allow for a non-Darcy flow. As indicated in Fig. 12, the advective flow was restricted by the bottleneck effect because of the low cross-sectional porosity in the normal direction to the bedding. The combination of the bottleneck pore structure, fast flow velocity, and opening out after narrow pore spaces resulted in high Re numbers and turbulent flow. In the experiments, the discharge values in the directions parallel and normal to the bedding were 5.46 × 10−6 m3/s and 6.41 × 10−7 m3/s, respectively; the kinematic viscosity of water at 40 °C was 6.58 × 10−7 m2/s; the characteristic length was 2.64 × 10−2 m which was assumed to be the diameter of the total pore spaces of the cross section with a diameter of 50 mm; and the porosity was 18.29%. \( Re^{||} \) and \( Re^{ \bot } \) were 5.50 and 0.58, respectively. In real flow, Re is dependent on the size of each pore. Even though it is difficult to determine the value of Re in the experiment, Re = 2 in the LBM simulation represents an appropriate value, which is of the order of the experimental Re. Using 2-D LBM for a virtual pore structure, Sato and Takeda (2016) pointed out that the fluid pressure mainly drops at pore throats. Therefore, turbulent flow is unlikely to occur under low flow rate conditions, and hence, the permeability anisotropy is reduced. They conducted their LBM simulation at Re = 0.1, which would not allow turbulent flow to occur. In the case of LBM simulation for pore structure of Berea sandstone at Re = 0.1, the results of k‖ = 1.37 × 10−12 m2 and k⊥ = 3.23 × 10−13 m2 were derived. The anisotropic permeability ratio (k⊥/k‖) was 4.24, which is smaller than the permeability ratio of 8.50 at Re = 2. Clearly, the bottleneck effect is reduced under the no turbulent flow condition due to a low flow velocity.

4.3 Comparison of the Permeability and Diffusivity Anisotropies

In the experimental results, the anisotropy ratios of the permeability (k⊥/k‖) and diffusivity (D ⊥e /D ‖e ) were 8.50 and 1.39, respectively. This indicates that the pore structure anisotropy of the bedding had a stronger effect on the permeability than on the diffusivity. As shown in Fig. 12, the flow velocity was restricted by the bottleneck effect because of the low cross-sectional porosity (7.87%) in the normal direction to the bedding. In the parallel direction to the bedding plane, the minimum cross-sectional porosity was 14.1%, and a gradual decrease in fluid pressure was apparent. The diffusivity in each direction was calculated by using tortuosity with porosity. The calculated diffusivity ratio (D ⊥e /D ‖e ) was less than the experimental results. This can be attributed to expanding a specific pore structure to the experimental sample block which is similar to extrapolating one bedding plane to a block layer.

In the case of ionic diffusion, ions can pass through the existing narrow pore spaces. This made the anisotropic diffusivity ratio smaller than the anisotropic permeability ratio. Peng et al. (2014) showed that 5.92 µm is a sufficiently high resolution to capture the main flow paths for the rock and that the smaller pores need not always be resolved. For ionic diffusion, however, Kikuchi et al. (2010) suggested that Cl− is restricted to pore radii of 6 nm or higher. This work focused on the separate phenomena on permeability and diffusion parameters. Further high-resolution simulations are needed to shed light on the limit values for the permeability and diffusivity.

5 Conclusions

In this study, the effect of pore structure on the transport parameters’ anisotropy in Berea sandstone, whose grain arrangement is dominated by sedimentation, was scrutinized. Implementing both experimental and numerical modeling approaches, the anisotropy ratios for the intrinsic permeability (k⊥/k‖) and effective diffusion coefficient (D ⊥e /D ‖e ) were estimated as 8.50 and 1.39, respectively. The difference in the ratios suggests that a preferentially oriented pore structure affects the permeability and diffusivity anisotropies in a meaningful manner. The advective flow in the normal and parallel directions to the bedding was simulated by LBM using a 3-D pore structure obtained from X-ray CT. The flow simulation results showed that the fluid pressures decreased primarily at areas of minimum cross-sectional porosity in the normal direction to the bedding. In the parallel direction to the bedding, the pressure gradually decreased with distance from the inflow boundary. The anisotropic diffusivity ratio was less than the anisotropic permeability ratio because, in the case of NaCl diffusion, ions can pass through very narrow pore spaces. The proposed bulk constrictivity in this study is the corresponding value of a sample’s specific pore structure on one bedding plane. Based on the experimental results, CT analysis, and LBM simulation, expanding one specific pore structure to an experimental sample of one block can be assumed to be similar to expanding one bedding plane to one block layer. The results suggest that the minimum cross-sectional porosity, which affects the permeability anisotropy by physically restricting moving elements, is still too large to induce anisotropic ionic diffusion. Such observations can pave the way for further investigation on the permeability and diffusivity anisotropy effects in reservoir modeling projects for geologic disposal of highly contaminant waste, hydrocarbon recovery, or storing CO2 in porous subsurface formations, rendering more comprehensive design considerations.