Lattice Boltzmann Simulation of Immiscible Displacement in Porous Media: Viscous Fingering in a Shear-Thinning Fluid

Abstract

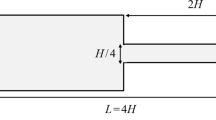
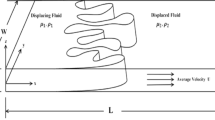
In this work, we investigate immiscible displacement in porous media with the displaced fluid being shear-thinning. We focus on the influence the heterogeneous viscosity field in the shear-thinning fluid brings on viscous fingering, which has received little attention in the existing researches. Lattice Boltzmann simulations of immiscible displacement with a power law model implementation in the displaced fluid are conducted. The lattice Boltzmann algorithm is validated against Newtonian and non-Newtonian flows in a channel. The effects of the shear-thinning property and the viscosity heterogeneity on viscous fingering are considered in the simulations. The results show that with stronger shear-thinning property (lower power law exponent n), there is stronger viscosity heterogeneity in the displaced fluid, and the viscous fingering shows weaker instability. The influence of a heterogeneous viscosity field on viscous fingering is dominated by the viscosity in the low-viscosity regions, while the high-viscosity regions show little influence. The influence of the local viscosity on viscous fingering is dependent upon the local shear rate. A concept of ‘effective field viscosity’ is introduced to quantitatively characterize a heterogeneous viscosity field. A shear rate weighted averaging algorithm is proposed to calculate the effective field viscosity from a heterogeneous viscosity field. The algorithm is tested in several cases and shows good performance to represent the influence of the heterogeneous viscosity field.

Appendix

The variables in Eqs. 1 and 2 are calculated using the subsequent algorithms. $\varGamma _i(\mathbf u )$ is calculated from

$$\begin{aligned} \varGamma _i(\mathbf{u })=w_i\left[ 1+\frac{\mathbf{e }_i\cdot \mathbf{u }}{c_s^2}+\frac{(\mathbf{e }_i\cdot \mathbf{u })^2}{2c_s^4}-\frac{\mathbf{u }^2}{2c_s^2}\right] . \end{aligned}$$

(13)

The equilibrium distribution functions $f_i^\mathrm{eq}$ and $g_i^\mathrm{eq}$ are written as

$$\begin{aligned} f_i^{eq}= & {} w_i\phi \left[ 1+\frac{\mathbf{e }_i\cdot \mathbf{u }}{c_s^2}+\frac{(\mathbf{e }_i\cdot \mathbf{u })^2}{2c_s^4}-\frac{\mathbf{u }^2}{2c_s^2}\right] . \end{aligned}$$

(14)

$$\begin{aligned} g_i^{eq}= & {} w_i\left[ p+\rho c_s^2\left( \frac{\mathbf{e }_i\cdot \mathbf{u }}{c_s^2}+\frac{(\mathbf{e }_i\cdot \mathbf{u })^2}{2c_s^4}-\frac{\mathbf{u }^2}{2c_s^2}\right) \right] . \end{aligned}$$

(15)

In the two-dimensional nine-velocity (D2Q9) model adopted in the present work, the velocity vectors are

$$\begin{aligned} \mathbf e _i=\left\{ \begin{array}{ll} [0,0] &{} i=0 \\ \quad \left[ \cos \left( \frac{(i-1)\pi }{2}\right) ,\sin \left( \frac{(i-1)\pi }{2}\right) \right] &{} i=1,2,3,4\\ \sqrt{2}\left[ \cos \left( \frac{(i-5)\pi }{2}+\frac{\pi }{4}\right) ,\sin \left( \frac{(i-5)\pi }{2}+\frac{\pi }{4}\right) \right] &{} i=5,6,7,8 \end{array} \right. \end{aligned}$$

(16)

The weighting coefficients are $w_0=\frac{4}{9},w_i=\frac{1}{9},i=1,2,3,4,w_i=\frac{1}{36},i=5,6,7,8$.

At each time step, the index function $\phi$, the pressure field p and the velocity field $\mathbf u$ are calculated from

$$\begin{aligned} \left\{ \begin{array}{ll} \phi =\sum f_i\\ \displaystyle p=\sum g_i-\frac{1}{2}{} \mathbf u \cdot \nabla \psi (\rho )\delta _t\\ \displaystyle \mathbf u =\frac{1}{\rho c_s^2}+\frac{1}{2\rho }(\mathbf F _s+\mathbf G )\delta _t \end{array}\right. \end{aligned}$$

(17)

The density field and the kinematic viscosity can be calculated from

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \rho (\phi )=\rho _l+\frac{\phi -\phi _l}{\phi _h-\phi _l}(\rho _h-\rho _l)\\ \displaystyle \nu (\phi )=\nu _l+\frac{\nu -\nu _l}{\nu _h-\nu _l}(\nu _h-\nu _l) \end{array}\right. \end{aligned}$$

(18)

where $\rho _l$ and $\rho _h$ are the densities of the lighter and heavier fluid, $\nu _l$ and $\nu _h$ are the kinematic viscosities of the lighter and heavier fluid, respectively. $\phi _l$ and $\phi _h$ are the index constants, respectively, corresponding to the lighter and heavier fluids, which are given as $\phi _l=0.02381$ and $\phi _h=0.2508$ (Zhang et al. 2000). In this model, the density ratio of the two fluids are limited to about 15 (Fakhari and Rahimian 2010). Numerical instability arises with density ratio exceeding this value.

The surface tension $F_s$ and the body force G are calculated from

$$\begin{aligned} \left\{ \begin{array}{ll} F_s=\kappa \phi \nabla \nabla ^2\phi \\ G=(\rho -\rho _m)g \end{array}\right. \end{aligned}$$

(19)

where $\kappa$ is a free parameter controlling the surface tension magnitude, $\rho _m$ is the mean density, g is the gravitational acceleration.

In non-ideal fluid conditions, $\nabla \psi (\rho ))=\nabla (p-c_s^2\rho )$ keeps the separations of phases, $\nabla \psi (\phi )$ determines the physical intermolecular interactions. The Carnahan–Starling fluid equation of state is adopted specifying $\psi (\phi )$ as

$$\begin{aligned} \psi (\phi )=c_s^2\phi \left[ \frac{1+\phi +\phi ^2-\phi ^3}{(1-\phi )^3}-1\right] -a\phi ^2 \end{aligned}$$

(20)

where a is a parameter to control the strength of molecular interactions. The critical value of Carnahan–Starling equation of state Norman (1969) is $a_c=3.53374$. For $a>a_c$, the fluids remain immiscible. Too large a values may cause numerical instabilities. In this work, we choose $a=4$ to comprise between immiscibility and numerical stability. $\nabla \psi$ and $\nabla ^2\psi$ are calculated with a forth-order compact scheme proposed by Lee and Lin (2005).