A Semi-Analytical Model for Characterizing the Pressure Transient Behavior of Finite-Conductivity Horizontal Fractures

Abstract

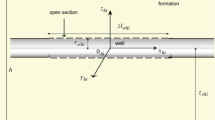
Hydraulic fracturing may induce horizontal fractures in shallow, tectonically active or high-reservoir-pressure formations. Studying the pressure transient behavior of the horizontal fractures can provide insights into the size and shape of the formations as well as their productivities. However, our knowledge about the pressure transient behavior of a horizontal fracture is far from adequate. In this study, a semi-analytical model is proposed to characterize the pressure transient behavior of finite-conductivity horizontal fractures in bounded reservoirs. Specifically, we discretize the horizontal fracture into rectangle plane elements, each of which is treated as a plane source. (In this work, a plane source indicates a rectangle plane, and the oil flows from the matrix to this plane.) The transient flow in the fracture systems can be numerically characterized with the finite difference method, whereas the transient flow in the matrix system can be analytically simulated with the Green function method; as such, the flow behavior in both the fracture and matrix can be modeled. Subsequently, we construct the mathematical model by coupling the finite difference formulations for the fracture system and the analytical functions for the matrix system. This semi-analytical model is arranged into a matrix format and can be readily solved with the Gaussian elimination method. The key features of the proposed approach can be summarized as: it can model an irregular horizontal fracture by discretizing the horizontal fracture into small elements, such that the real fracture configuration can be better captured; the fracture conductivity can be taken into consideration; and the non-uniform influx distribution along the fracture can be modeled to better honor the actual flow behavior from the matrix to the fracture. We also apply the semi-analytical method to analyze the flow regimes of single-phase oil flow from a circular horizontal fracture and an elliptical horizontal fracture in a bounded reservoir; the flow regimes such as wellbore after flow, bilinear flow, formation linear flow, early pseudo-radial flow, late pseudo-radial flow, elliptical flow, and boundary dominated flow can be observed during oil production. In addition, we examine the influences of formation thickness, fracture’s vertical position, fracture conductivity, and wellbore storage on the pressure dynamics of a circular horizontal fracture. It is found that the early pseudo-radial flow results from two different flow scenarios: one is near the edge of the horizontal fracture when the formation thickness is small, while the other one is surrounding the horizontal fracture in the vertical direction when the formation thickness is sufficiently large. The wellbore storage mainly exerts influences on the early production period, and its duration tends to be longer as the fracture conductivity decreases. Furthermore, the flow regimes and pseudo-skin factor are comprehensively investigated for an elliptical horizontal fracture and an irregular-shaped horizontal fracture that may be induced by the stress heterogeneity in the reservoirs.

Appendices

Appendix A: Numerical Solution for the Oil Flow in the Horizontal Fracture

The 2D continuity equation is given as (Ertekin et al. 2001):

$$ - \frac{\partial }{\partial x}\left( {\rho u_{x} } \right) - \frac{\partial }{\partial y}\left( {\rho u_{y} } \right) - \frac{\partial }{\partial z}\left( {\rho u_{z} } \right) + \frac{{q_{\text{sc}} \rho_{\text{sc}} }}{{V_{b} }} = \frac{\partial }{\partial t}\left( {\rho \phi } \right) $$

(A-1)

where ρ is fluid density, u _x , u _y , and u _z are Darcy flow rate, V_b is bulk volume, and for a single fracture element V_b = w∆x _i,j ∆y _i,j . Equation (A-1) is a partial differential equation, and we can solve it with finite difference method. Implicit finite difference method is utilized in this work because the results of implicit finite difference method are more stable than the explicit finite difference method. The finite difference approximation in this work is based on 5-point scheme, which has a truncation error proportional to (∆x)² (or (∆y)²) and ∆t. The implicit finite difference approximation based on the 5-point scheme can provide sufficiently accurate results for simulating the transient fracture flow. Multiplying Eq. (A-1) by the bulk volume gives:

$$ - \frac{\partial }{\partial x}\left( {\rho u_{x} w\Delta y} \right)_{i,j} \Delta x_{i,j} - \frac{\partial }{\partial y}\left( {\rho u_{y} w\Delta x} \right)_{i,j} \Delta y_{i,j} + q_{{{\text{sc}}_{i,j} }} \rho_{\text{sc}} = \left( {\Delta x\Delta yw} \right)_{i,j} \frac{\partial }{\partial t}\left( {\rho \phi } \right) $$

(A-2)

Based on Darcy equation, we have,

$$ \begin{aligned} u_{x} & = - \beta \frac{{k_{fx} }}{\mu }\frac{\partial p}{\partial x} \\ u_{y} & = - \beta \frac{{k_{fy} }}{\mu }\frac{\partial p}{\partial y} \\ \end{aligned} $$

(A-3)

and the formation volume factor is defined as:

$$ B = \frac{{\rho_{\text{sc}} }}{\rho } $$

(A-4)

For a slightly compressible fluid, we have

$$ \rho = \rho_{0} \left[ {1 + c_{l} \left( {p - p_{0} } \right)} \right] $$

(A-5)

where c_l is fluid compressibility and p₀ and ρ₀ are reference pressure and reference density, respectively. For the porous media, we have

$$ \phi = \phi_{0} \left[ {1 + c_{\text{f}} \left( {p - p_{0} } \right)} \right] $$

(A-6)

The fracture total compressibility is given as:

$$ c_{\text{tf}} = c_{\text{f}} + c_{\text{l}} $$

(A-7)

where ϕ₀ is reference porosity, and c_f is compressibility of the matrix or fracture. Inserting Eqs. (A-3) to (A-7) into Eq. (A-2) yields:

$$ \begin{aligned} & \frac{\partial }{\partial x}\left( {\beta \frac{{\Delta ywk_{fx} }}{\mu B}\frac{\partial p}{\partial x}} \right)_{i,j} \Delta x_{i,j} + \frac{\partial }{\partial y}\left( {\beta \frac{{\Delta xwk_{fy} }}{\mu B}\frac{\partial p}{\partial y}} \right)_{i,j} \Delta y_{i,j} \\ & \quad + q_{{{\text{sc}}_{i,j} }} = \left( {\frac{{\Delta x\Delta yw\phi_{\text{f}} c_{\text{tf}} }}{B}} \right)_{i,j} \frac{{\partial p_{i,j} }}{\partial t} \\ \end{aligned} $$

(A-8)

Applying the finite difference approximation to the first term on the left-hand side of Eq. (A-8), we can have:

$$ \frac{\partial }{\partial x}\left( {\beta \frac{{\Delta ywk_{x} }}{\mu B}\frac{\partial p}{\partial x}} \right)_{i,j} \approx \frac{1}{{\Delta x_{i,j} }}\left[ {\left( {\beta \frac{{\Delta ywk_{x} }}{\mu B}\frac{\partial p}{\partial x}} \right)_{{i + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} - \left( {\beta \frac{{\Delta ywk_{x} }}{\mu B}\frac{\partial p}{\partial x}} \right)_{{i - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} } \right] $$

(A-9)

where

$$ \left( {\frac{\partial p}{\partial x}} \right)_{{i + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} \approx \frac{{p_{i + 1,j} - p_{i,j} }}{{\Delta x_{{i + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} }} $$

(A-10)

and

$$ \left( {\frac{\partial p}{\partial x}} \right)_{{i - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} \approx \frac{{p_{i,j} - p_{i - 1,j} }}{{\Delta x_{{i - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} }} $$

(A-11)

Thus, Eq. (A-9) can be written as:

$$ \begin{aligned} \frac{\partial }{\partial x}\left( {\beta \frac{{\Delta ywk_{fx} }}{\mu B}\frac{\partial p}{\partial x}} \right)_{i,j} \Delta x_{i,j} & { = }\left( {\beta \frac{{\Delta ywk_{fx} }}{\mu B\Delta x}} \right)_{{i + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} \left( {p_{i + 1,j}^{n} - p_{i,j}^{n} } \right) \\ & \quad - \left( {\beta \frac{{\Delta ywk_{fx} }}{\mu B\Delta x}} \right)_{{i - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} \left( {p_{i,j}^{n} - p_{i - 1,j}^{n} } \right) \\ \end{aligned} $$

(A-12)

Similarly, the second term on the left-hand side of Eq. (A-8) can be rewritten as:

$$ \begin{aligned} \frac{\partial }{\partial y}\left( {\beta \frac{{\Delta xwk_{fy} }}{\mu B}\frac{\partial p}{\partial y}} \right)_{i,j} \Delta y_{i,j} & = \left( {\beta \frac{{\Delta xwk_{fy} }}{\mu B\Delta y}} \right)_{{i,j + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {p_{i,j + 1}^{n} - p_{i,j}^{n} } \right) \\ & \quad - \left( {\beta \frac{{\Delta xwk_{fy} }}{\mu B\Delta y}} \right)_{{i,j - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {p_{i,j}^{n} - p_{i,j - 1}^{n} } \right) \\ \end{aligned} $$

(A-13)

Applying backward-difference approximation on the time derivative, we can obtain:

$$ \frac{{\partial p_{i,j} }}{\partial t} \approx \frac{{p_{i,j}^{n} - p_{i,j}^{n - 1} }}{\Delta t} $$

(A-14)

The backward-difference approximation of the flow equation can be written as:

$$ \begin{aligned} & \left( {\beta \frac{{\Delta ywk_{fx} }}{\mu B\Delta x}} \right)_{{i + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} \left( {p_{i + 1,j}^{n} - p_{i,j}^{n} } \right) - \left( {\beta \frac{{\Delta ywk_{fx} }}{\mu B\Delta x}} \right)_{{i - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},j}} \left( {p_{i,j}^{n} - p_{i - 1,j}^{n} } \right) \\ & \quad + \,\left( {\beta \frac{{\Delta xwk_{fy} }}{\mu B\Delta y}} \right)_{{i,j + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {p_{i,j + 1}^{n} - p_{i,j}^{n} } \right) - \left( {\beta \frac{{\Delta xwk_{fy} }}{\mu B\Delta y}} \right)_{{i,j - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {p_{i,j}^{n} - p_{i,j - 1}^{n} } \right) \\ & \quad + \,q_{{{\text{sc}}_{i,j} }} = \left( {\frac{{\Delta x\Delta yw\phi_{f} c_{tf} }}{B\Delta t}} \right)_{i,j} \left( {p_{i,j}^{n} - p_{i,j}^{n - 1} } \right) \\ \end{aligned} $$

(A-15)

Equation (A-15) can be used to characterize the transient flow in the fracture system. This equation is also applicable if the fracture has non-uniform fracture width and fracture conductivity distribution. In this work, we assume that the fracture width and fracture conductivity are both uniform along the fracture; thus, Eq. (A-15) can be simplified as:

$$ \begin{aligned} & \beta \frac{{\Delta y_{i,j} wk_{f} }}{\mu B\Delta x}\left( {p_{i + 1,j}^{n} - 2p_{i,j}^{n} + p_{i - 1,j}^{n} } \right) + \beta \frac{{\Delta x_{i,j} wk_{f} }}{\mu B\Delta y}\left( {p_{i,j + 1}^{n} - 2p_{i,j}^{n} + p_{i,j - 1}^{n} } \right) \\ & \quad + \,q_{{{\text{sc}}_{i,j} }} = \frac{{\Delta x_{i,j} \Delta y_{i,j} w\phi_{f} c_{tf} }}{B\Delta t}\left( {p_{i,j}^{n} - p_{i,j}^{n - 1} } \right) \\ \end{aligned} $$

(A-16)

In particular, for the well-element, the approximated flow equation can be written as:

$$ \begin{aligned} & \beta \frac{{\Delta y_{i,j} wk_{f} }}{\mu B\Delta x}\left( {p_{i + 1,j}^{n} - 2p_{i,j}^{n} + p_{i - 1,j}^{n} } \right) + \beta \frac{{\Delta x_{i,j} wk_{f} }}{\mu B\Delta y}\left( {p_{i,j + 1}^{n} - 2p_{i,j}^{n} + p_{i,j - 1}^{n} } \right) \\ & \quad + q_{{{\text{sc}}_{i,j} }} - q_{f - w} = \frac{{\Delta x_{i,j} \Delta y_{i,j} w\phi_{f} c_{tf} }}{B\Delta t}\left( {p_{i,j}^{n} - p_{i,j}^{n - 1} } \right) \\ \end{aligned} $$

(A-17)

Non-dimensionalizing the variables in Eqs. (A-16) and (A-17) based on Table 1 yields,

$$ \begin{aligned} & \frac{{C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}\left( {2p_{{{\text{fD}}_{i,j} }}^{n} - p_{{{\text{fD}}_{i + 1,j} }}^{n} - p_{{{\text{fD}}_{i - 1,j} }}^{n} } \right) + \frac{{C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}\left( {2p_{{{\text{fD}}_{i,j} }}^{n} - p_{{{\text{fD}}_{i,j + 1} }}^{n} - p_{{{\text{fD}}_{i,j - 1} }}^{n} } \right) \\ & \quad + \frac{{2\pi h_{D} }}{{\Delta x_{\text{D}} \Delta y_{\text{D}} w_{\text{D}} C_{\text{s}} }}q_{{{\text{fD}}_{i,j} }}^{n} = \frac{1}{{\Delta t_{\text{D}} }}\left( {p_{{{\text{fD}}_{i,j} }}^{n - 1} - p_{{{\text{fD}}_{i,j} }}^{n} } \right) \\ \end{aligned} $$

(A-18)

and

$$ \begin{aligned} & \frac{{C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}\left( {2p_{{{\text{fD}}_{i,j} }}^{n} - p_{{{\text{fD}}_{i + 1,j} }}^{n} - p_{{{\text{fD}}_{i - 1,j} }}^{n} } \right) + \frac{{C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}\left( {2p_{{{\text{fD}}_{i,j} }}^{n} - p_{{{\text{fD}}_{i,j + 1} }}^{n} - p_{{{\text{fD}}_{i,j - 1} }}^{n} } \right) \\ & \quad + \frac{{2\pi h_{\text{D}} }}{{\Delta x_{\text{D}} \Delta y_{\text{D}} w_{\text{D}} C_{\text{s}} }}\left( {q_{{{\text{fD}}_{i,j} }}^{n} - q_{{f{ - }w{\text{D}}}}^{n} } \right) = \frac{1}{{\Delta t_{\text{D}} }}\left( {p_{{{\text{fD}}_{i,j} }}^{n - 1} - p_{{{\text{fD}}_{i,j} }}^{n} } \right) \\ \end{aligned} $$

(A-19)

Rearranging Eqs. (A-18) and (A-19) gives the following:

$$ \begin{aligned} & \left( {\frac{{2C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }} + \frac{{2C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }} + \frac{1}{{\Delta t_{\text{D}} }}} \right)p_{{{\text{fD}}_{i,j} }}^{n} - \frac{{2C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{i - 1,j} }}^{n} - \frac{{C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{i,j - 1} }}^{n} \\ & \quad - \frac{{2C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{i + 1,j} }}^{n} - \frac{{C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{i,j + 1} }}^{n} + \frac{{2\pi h_{D} }}{{\Delta x_{\text{D}} \Delta y_{\text{D}} w_{\text{D}} C_{\text{s}} }}q_{{{\text{fD}}_{i,j} }}^{n} = \frac{1}{{\Delta t_{\text{D}} }}p_{{{\text{fD}}_{i,j} }}^{n - 1} \\ \end{aligned} $$

(A-20)

$$ \begin{aligned} & \left( {\frac{{2C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }} + \frac{{2C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }} + \frac{1}{{\Delta t_{\text{D}} }}} \right)p_{{{\text{fD}}_{i,j} }}^{n} - \frac{{2C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{i - 1,j} }}^{n} - \frac{{C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{\text{i,j - 1}} }}^{n} \\ & \quad - \frac{{2C_{\text{fD}} }}{{\Delta x_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{i + 1,j} }}^{n} - \frac{{C_{\text{fD}} }}{{\Delta y_{\text{D}}^{2} w_{\text{D}} C_{\text{s}} }}p_{{{\text{fD}}_{i,j + 1} }}^{n} \\ & \quad + \frac{{2\pi h_{D} }}{{\Delta x_{\text{D}} \Delta y_{\text{D}} w_{\text{D}} C_{\text{s}} }}q_{{{\text{fD}}_{i,j} }}^{n} - \frac{{2\pi h_{\text{D}} }}{{\Delta x_{\text{D}} \Delta y_{\text{D}} w_{\text{D}} C_{\text{s}} }}q_{{f{ - }w{\text{D}}}}^{n} = \frac{1}{{\Delta t_{\text{D}} }}p_{{{\text{fD}}_{i,j} }}^{n - 1} \\ \end{aligned} $$

(A-21)

As such, in Eqs. (A-20) and (A-21), the dimensionless pressures, dimensionless withdrawal rates, and dimensionless flux from fracture to wellbore on the LHS become the unknowns. The flow equations for the N_f facture elements can be then written in a matrix form,

$$ \left[ {\begin{array}{*{20}c} A & a \\ \end{array} } \right] \cdot \left[ \begin{array}{c} \, p_{\text{fD}} \hfill \\ \, q_{\text{fD}} \hfill \\ q_{{f{ - }w{\text{D}}}}^{n} \hfill \\ \end{array} \right] = {\text{RHS}}_{1} $$

(A-22)

where

$$ \begin{aligned} & a = \left[ \begin{array}{l} \, \left. \begin{array}{l} 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ \end{array} \right\}n_{w} - 1 \hfill \\ - \frac{{2\pi h_{\text{D}} }}{{\Delta x_{\text{D}} \Delta y_{\text{D}} w_{\text{D}} C_{\text{s}} }} \hfill \\ \, 0 \hfill \\ \, 0 \hfill \\ \, \vdots \hfill \\ \, 0 \hfill \\ \end{array} \right]_{{N_{\text{f}} \times 1}} ,\,p_{\text{fD}} = \left[ \begin{array}{l} p_{{{\text{fD}}_{1} }}^{n} \hfill \\ \, \vdots \hfill \\ p_{{{\text{fD}}_{nw} }}^{n} \hfill \\ \, \vdots \hfill \\ p_{{{\text{fD}}_{{N_{\text{f}} }} }}^{n} \hfill \\ \end{array} \right]_{{N_{\text{f}} \times 1}} , \\ & {\mathbf{q}}_{\text{fD}} { = }\left[ \begin{array}{l} q_{{{\text{fD}}_{1} }}^{n} \hfill \\ \, \vdots \hfill \\ q_{{{\text{fD}}_{nw} }}^{n} \hfill \\ \, \vdots \hfill \\ q_{{{\text{fD}}_{{N_{\text{f}} }} }}^{n} \hfill \\ \end{array} \right]_{{N_{\text{f}} \times 1}} \,{\text{and}}\,{\text{RHS}}_{1} = \left[ \begin{array}{l} \frac{1}{{\Delta t_{\text{D}} }}p_{{{\text{fD}}_{1} }}^{n - 1} \hfill \\ \, \vdots \hfill \\ \frac{1}{{\Delta t_{\text{D}} }}p_{{{\text{fD}}_{nw} }}^{n - 1} \hfill \\ \, \vdots \hfill \\ \frac{1}{{\Delta t_{\text{D}} }}p_{{{\text{fD}}_{{N_{\text{f}} }} }}^{n - 1} \hfill \\ \end{array} \right]_{{N_{\text{f}} \times 1}} , \\ \end{aligned} $$

where A is a matrix with a dimension of N_f × 2N_f and it represents the coefficients of the dimensionless pressures and the coefficients of dimensionless withdrawal rates of the fracture elements in Eqs. (A-20) and (A-21), and n_w is the number of the well-element.

Appendix B: Analytical Solution for the Oil Flow in the Reservoir Matrix

Figure 22 shows a line source in a bounded reservoir and a plane source in a bounded reservoir, respectively. In a 2D reservoir, the pressure response at position x at time t caused by an instantaneous line source which is activated at time t₀ is given by Gringarten and Ramey (1973):

$$ \begin{aligned} & p_{i} - \tilde{p}\left( {x,t} \right) \\ & = \frac{\delta }{{\phi_{\text{m}} c_{\text{tm}} }}\frac{1}{{x_{e} }}\left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} } \right)}}{{x_{e}^{2} }}} \right]\cos \frac{{m\pi x_{0} }}{{x_{e} }}\cos \frac{m\pi x}{{x_{e} }}} } \right\} \\ \end{aligned} $$

(B-1)

where δ is the withdrawal rate per unit length, unit area or unit volume. Equation (B-1) is derived using the Green function method. Similarly, the following equation can be used to predict the pressure response at position x at time t caused by an instantaneous plane source which is activated at time t₀,

$$ \begin{aligned} & p_{i} - \tilde{p}\left( {x,t} \right) \\ & = \frac{\delta }{{\phi_{\text{m}} c_{\text{tm}} }}\frac{{x_{\text{f}} }}{{x_{e} }}\left\{ {1 + \frac{{4x_{e} }}{\pi \Delta x}\sum\limits_{m = 1}^{\infty } {\frac{1}{n}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} } \right)}}{{x_{e}^{2} }}} \right]\sin \frac{m\pi \Delta x}{{2x_{e} }}\cos \frac{{m\pi x_{0} }}{{x_{e} }}\cos \frac{m\pi x}{{x_{e} }}} } \right\} \\ \end{aligned} $$

(B-2)

where ∆x is the width of the plane source.

Fig. 22

A line source and a plane source in a 2D reservoir: a a line source in a bounded reservoir; and b a plane source in a bounded reservoir

Figure 23 shows a plane source in a 3D bounded reservoir. According to the Newman product principle, the pressure response of an instantaneous plane source in a 3D reservoir can be obtained by the product of a plane source in X direction and a plane source in Y direction and a line source in Z direction:

$$ \begin{aligned} & p_{i} - \widetilde{p}\left( {x,y,z,t} \right) \\ & = \frac{\delta }{{\phi_{\text{m}} c_{\text{tm}} }}\frac{{x_{\text{f}} }}{{x_{e} }}\left\{ {1 + \frac{{4x_{e} }}{\pi \Delta x}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} } \right)}}{{x_{e}^{2} }}} \right]\sin \frac{m\pi \Delta x}{{2x_{e} }}\cos \frac{{m\pi x_{0} }}{{x_{e} }}\cos \frac{m\pi x}{{x_{e} }}} } \right\} \\ & \quad \cdot \frac{{y_{\text{f}} }}{{y_{e} }}\left\{ {1 + \frac{{4y_{e} }}{\pi \Delta y}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} } \right)}}{{y_{e}^{2} }}} \right]\sin \frac{m\pi \Delta y}{{2y_{e} }}\cos \frac{{m\pi y_{0} }}{{y_{e} }}\cos \frac{m\pi y}{{y_{e} }}} } \right\} \\ & \quad \cdot \frac{1}{{z_{e} }}\left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} } \right)}}{{z_{e}^{2} }}} \right]\cos \frac{{m\pi z_{0} }}{{z_{e} }}\cos \frac{m\pi z}{{z_{e} }}} } \right\} \\ \end{aligned} $$

(B-3)

The pressure response at point (x, y, z) at time t due to the contribution by a continuous plane source with a withdrawal rate of q_sc can be calculated by:

$$ \begin{aligned} & p_{i} - p\left( {x,y,z,t} \right) \\ & = \frac{{\hat{q}\left( t \right)}}{{\phi_{m} c_{tm} }}\int_{0}^{{t - t_{0} }} {\frac{{x_{\text{f}} }}{{x_{e} }}\left\{ {1 + \frac{{4x_{e} }}{\pi \Delta x}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} - \tau } \right)}}{{x_{e}^{2} }}} \right]\sin \frac{m\pi \Delta x}{{2x_{e} }}\cos \frac{{m\pi x_{0} }}{{x_{e} }}\cos \frac{m\pi x}{{x_{e} }}} } \right\}} \\ & \quad \cdot \frac{{y_{\text{f}} }}{{y_{e} }}\left\{ {1 + \frac{{4y_{e} }}{\pi \Delta y}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} - \tau } \right)}}{{y_{e}^{2} }}} \right]\sin \frac{m\pi \Delta y}{{2y_{e} }}\cos \frac{{m\pi y_{0} }}{{y_{e} }}\cos \frac{m\pi y}{{y_{e} }}} } \right\} \\ & \cdot \quad \frac{1}{{z_{e} }}\left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} - \tau } \right)}}{{z_{e}^{2} }}} \right]\cos \frac{{m\pi z_{0} }}{{z_{e} }}\cos \frac{m\pi z}{{z_{e} }}} } \right\}{\text{d}}\tau \\ \end{aligned} $$

(B-4)

where

$$ \hat{q}\left( t \right){ = }\frac{q\left( t \right)}{{x_{\text{f}} y_{\text{f}} }}{ = }\frac{{Bq_{\text{sc}} \left( t \right)}}{{x_{\text{f}} y_{\text{f}} }} $$

(B-5)

Fig. 23

A plane source in a 3D bounded reservoir

Thus, Eq. (B-4) can be written as:

$$ \begin{aligned} & p_{i} - p\left( {x,y,z,t} \right) \\ &\quad = \frac{{Bq_{\text{sc}} \left( t \right)}}{{\phi_{\text{m}} c_{\text{tm}} x_{e} y_{e} z_{e} }}\int_{0}^{{t - t_{0} }} {\left\{ {1 + \frac{{4x_{e} }}{\pi \Delta x}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} - \tau } \right)}}{{x_{e}^{2} }}} \right]\sin \frac{m\pi \Delta x}{{2x_{e} }}\cos \frac{{m\pi x_{0} }}{{x_{e} }}\cos \frac{m\pi x}{{x_{e} }}} } \right\}} \\ &\qquad \cdot \left\{ {1 + \frac{{4y_{e} }}{\pi \Delta y}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} - \tau } \right)}}{{y_{e}^{2} }}} \right]\sin \frac{m\pi \Delta y}{{2y_{e} }}\cos \frac{{m\pi y_{0} }}{{y_{e} }}\cos \frac{m\pi y}{{y_{e} }}} } \right\} \\ &\qquad \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t - t_{0} - \tau } \right)}}{{z_{e}^{2} }}} \right]\cos \frac{{m\pi z_{0} }}{{z_{e} }}\cos \frac{m\pi z}{{z_{e} }}} } \right\}{\text{d}}\tau \\ \end{aligned} $$

(B-6)

In the production period, the withdrawal rate of a plane source is time dependent. The pressure response at position (x, y, z) at time tⁿ caused by a time-dependent continuous plane source is

$$ \begin{aligned} & p_{i} - p\left( {x,y,z,t^{n} } \right) = \frac{B}{{\phi_{\text{m}} c_{\text{tm}} x_{e} y_{e} z_{e} }}\sum\limits_{l = 1}^{l = n} {\left( {q_{\text{sc}}^{l} - q_{\text{sc}}^{l - 1} } \right)\int_{0}^{{t^{n} - t^{l - 1} }} {} } \\ & \left\{ {1 + \frac{{4x_{e} }}{\pi \Delta x}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t^{n} - t^{l - 1} - \tau } \right)}}{{x_{e}^{2} }}} \right]\sin \frac{m\pi \Delta x}{{2x_{e} }}\cos \frac{{m\pi x_{0} }}{{x_{e} }}\cos \frac{m\pi x}{{x_{e} }}} } \right\} \\ & \cdot \left\{ {1 + \frac{{4y_{e} }}{\pi \Delta y}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t^{n} - t^{l - 1} - \tau } \right)}}{{y_{e}^{2} }}} \right]\sin \frac{m\pi \Delta y}{{2y_{e} }}\cos \frac{{m\pi y_{0} }}{{y_{e} }}\cos \frac{m\pi y}{{y_{e} }}} } \right\} \\ & \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t^{n} - t^{l - 1} - \tau } \right)}}{{z_{e}^{2} }}} \right]\cos \frac{{m\pi z_{0} }}{{z_{e} }}\cos \frac{m\pi z}{{z_{e} }}} } \right\}{\text{d}}\tau \\ \end{aligned} $$

(B-7)

Since we discretize the horizontal fracture into N_f fracture elements, the pressure response at a given position (x, y, z) should be the summation of the pressure responses caused by all of the elements, leading to the following:

$$ \begin{aligned} & p_{i} - p\left( {x,y,z,t^{n} } \right) = \frac{B}{{\phi_{\text{m}} c_{\text{tm}} x_{e} y_{e} z_{e} }}\sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {\left( {q_{f,k}^{l} - q_{f,k}^{l - 1} } \right)\int_{0}^{{t^{n} - t^{l - 1} }} {} } } \\ & \left\{ {1 + \frac{{4x_{e} }}{{\pi \Delta x_{k} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t^{n} - t^{l - 1} - \tau } \right)}}{{x_{e}^{2} }}} \right]\sin \frac{{m\pi \Delta x_{k} }}{{2x_{e} }}\cos \frac{{m\pi x_{0,k} }}{{x_{e} }}\cos \frac{m\pi x}{{x_{e} }}} } \right\} \\ & \cdot \left\{ {1 + \frac{{4y_{e} }}{{\pi \Delta y_{k} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t^{n} - t^{l - 1} - \tau } \right)}}{{y_{e}^{2} }}} \right]\sin \frac{{m\pi \Delta y_{k} }}{{2y_{e} }}\cos \frac{{m\pi y_{0,k} }}{{y_{e} }}\cos \frac{m\pi y}{{y_{e} }}} } \right\} \\ & \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \alpha \left( {t^{n} - t^{l - 1} - \tau } \right)}}{{z_{e}^{2} }}} \right]\cos \frac{{m\pi z_{0,k} }}{{z_{e} }}\cos \frac{m\pi z}{{z_{e} }}} } \right\}{\text{d}}\tau \\ \end{aligned} $$

(B-8)

Equation (B-8) can be written in a dimensionless form,

$$ \begin{aligned} & p_{\text{D}}^{n} \left( {x_{\text{D}} ,y_{\text{D}} ,z_{\text{D}} ,t_{\text{D}}^{n} } \right) = \frac{2\pi }{{x_{{e{\text{D}}}} y_{{e{\text{D}}}} }}\sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {\left( {q_{{{\text{fD}},k}}^{l} - q_{{{\text{fD}},k}}^{l - 1} } \right)\int_{0}^{{t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} }} {} } } \\ & \left\{ {1 + \frac{{4x_{{e{\text{D}}}} }}{{\pi \Delta x_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{x_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta x_{{{\text{D}},k}} }}{{2x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{{0{\text{D}},k}} }}{{x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{\text{D}} }}{{x_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + \frac{{4y_{{e{\text{D}}}} }}{{\pi \Delta y_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{y_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta y_{{{\text{D}},k}} }}{{2y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{{0{\text{D}},k}} }}{{y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{\text{D}} }}{{y_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{z_{{e{\text{D}}}}^{2} }}} \right]\cos \frac{{m\pi z_{{0{\text{D}},k}} }}{{z_{{e{\text{D}}}} }}\cos \frac{{m\pi z_{\text{D}} }}{{z_{{e{\text{D}}}} }}} } \right\}{\text{d}}\tau_{\text{D}} \\ \end{aligned} $$

(B-9)

Based on Eq. (B-9), we can have,

$$ \begin{aligned} & p_{\text{D}}^{n - 1} \left( {x_{\text{D}} ,y_{\text{D}} ,z_{\text{D}} ,t_{\text{D}}^{n - 1} } \right) = \frac{2\pi }{{x_{{e{\text{D}}}} y_{{e{\text{D}}}} }}\sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n - 1} {\left( {q_{{{\text{fD}},k}}^{l} - q_{{{\text{fD}},k}}^{l - 1} } \right)\int_{0}^{{t_{\text{D}}^{n - 1} - t_{\text{D}}^{l - 1} }} {} } } \\ & \left\{ {1 + \frac{{4x_{{e{\text{D}}}} }}{{\pi \Delta x_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n - 1} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{x_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta x_{{{\text{D}},k}} }}{{2x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{{0{\text{D}},k}} }}{{x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{\text{D}} }}{{x_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + \frac{{4y_{{e{\text{D}}}} }}{{\pi \Delta y_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n - 1} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{y_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta y_{{{\text{D}},k}} }}{{2y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{{0{\text{D}},k}} }}{{y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{\text{D}} }}{{y_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n - 1} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{z_{{e{\text{D}}}}^{2} }}} \right]\cos \frac{{m\pi z_{{0{\text{D}},k}} }}{{z_{{e{\text{D}}}} }}\cos \frac{{m\pi z_{\text{D}} }}{{z_{{e{\text{D}}}} }}} } \right\}{\text{d}}\tau_{\text{D}} \\ \end{aligned} $$

(B-10)

Combining Eq. (B-9) with Eq. (B-10), we can have:

$$ \begin{aligned} & p_{\text{D}}^{n} \left( {x_{\text{D}} ,y_{\text{D}} ,z_{\text{D}} ,t_{\text{D}}^{n} } \right) = p_{\text{D}}^{n - 1} + \frac{2\pi }{{x_{{e{\text{D}}}} y_{{e{\text{D}}}} }}\sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {\left( {q_{{{\text{fD}},k}}^{l} - q_{{{\text{fD}},k}}^{l - 1} } \right)\int_{{t_{\text{D}}^{n - 1} - t_{\text{D}}^{l - 1} }}^{{t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} }} {} } } \\ & \left\{ {1 + \frac{{4x_{{e{\text{D}}}} }}{{\pi \Delta x_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{x_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta x_{{{\text{D}},k}} }}{{2x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{{0{\text{D}},k}} }}{{x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{\text{D}} }}{{x_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + \frac{{4y_{{e{\text{D}}}} }}{{\pi \Delta y_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{y_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta y_{{{\text{D}},k}} }}{{2y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{0D,k} }}{{y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{D} }}{{y_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{z_{{e{\text{D}}}}^{2} }}} \right]\cos \frac{{m\pi z_{{0{\text{D}},k}} }}{{z_{{e{\text{D}}}} }}\cos \frac{{m\pi z_{\text{D}} }}{{z_{{e{\text{D}}}} }}} } \right\}{\text{d}}\tau_{\text{D}} \\ \end{aligned} $$

(B-11)

As for a given fracture element, we use the dimensionless pressure at the center of this fracture element to represent the average pressure within this fracture element. Based on Eq. (B-11), the dimensionless pressure at the center of the fracture element can be obtained by:

$$ \begin{aligned} & p_{{{\text{fD}},g}}^{n} \left( {x_{{0{\text{D}},g}} ,y_{{0{\text{D}},g}} ,z_{{0{\text{D}},g}} ,t_{\text{D}}^{n} } \right) = p_{{{\text{fD}},g}}^{n - 1} + \frac{2\pi }{{x_{{e{\text{D}}}} y_{{e{\text{D}}}} }}\sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {\left( {q_{{{\text{fD}},k}}^{l} - q_{{{\text{fD}},k}}^{l - 1} } \right)\int_{{t_{\text{D}}^{n - 1} - t_{\text{D}}^{l - 1} }}^{{t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} }} {} } } \\ & \left\{ {1 + \frac{{4x_{{e{\text{D}}}} }}{{\pi \Delta x_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{x_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta x_{{{\text{D}},k}} }}{{2x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{{0{\text{D}},k}} }}{{x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{{0{\text{D}},g}} }}{{x_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + \frac{{4y_{{e{\text{D}}}} }}{{\pi \Delta y_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{y_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta y_{{{\text{D}},k}} }}{{2y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{{0{\text{D}},k}} }}{{y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{{0{\text{D}},g}} }}{{y_{{e{\text{D}}}} }}} \right\} \\ & \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{z_{{e{\text{D}}}}^{2} }}} \right]\cos \frac{{m\pi z_{{0{\text{D}},k}} }}{{z_{{e{\text{D}}}} }}\cos \frac{{m\pi z_{{0{\text{D}},g}} }}{{z_{{e{\text{D}}}} }}} } \right\}{\text{d}}\tau_{\text{D}} \\ \end{aligned} $$

(B-12)

where (x_0D,g, y_0D,g, z_0D,g) indicates the position of the center of the gth fracture element (g = 1, 2,… N_f) and p_fD,g indicates the dimensionless average pressure of the gth fracture element. For convenience, Eq. (B-12) can be also written as:

$$ p_{{{\text{fD}},g}}^{n} \left( {x_{{0{\text{D}},g}} ,y_{{0{\text{D}},g}} ,z_{{0{\text{D}},g}} ,t_{\text{D}}^{n} } \right) = p_{{{\text{fD}},g}}^{n - 1} + \sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {\left( {q_{{{\text{fD}},k}}^{l} - q_{{{\text{fD}},k}}^{l - 1} } \right)G_{l,k,g} } } $$

(B-13)

where

$$ \begin{aligned} G_{l,k,g} & = \frac{2\pi }{{x_{{e{\text{D}}}} y_{{e{\text{D}}}} }}\int_{{t_{\text{D}}^{n - 1} - t_{\text{D}}^{l - 1} }}^{{t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} }} {} \\ & \cdot \left\{ {1 + \frac{{4x_{{e{\text{D}}}} }}{{\pi \Delta x_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{x_{{e{\text{D}}}}^{2} }}} \right]\sin \frac{{m\pi \Delta x_{{{\text{D}},k}} }}{{2x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{{0{\text{D}},k}} }}{{x_{{e{\text{D}}}} }}\cos \frac{{m\pi x_{{0{\text{D}},g}} }}{{x_{{e{\text{D}}}} }}} } \right\} \\ & \quad \cdot \left\{ {1 + \frac{{4y_{{e{\text{D}}}} }}{{\pi \Delta y_{{{\text{D}},k}} }}\sum\limits_{m = 1}^{\infty } {\frac{1}{m}\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{y_{{e{\text{D}}}}^{2} }}} \right]} } \right. \\ & \left. {\sin \frac{{m\pi \Delta y_{{{\text{D}},k}} }}{{2y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{{0{\text{D}},k}} }}{{y_{{e{\text{D}}}} }}\cos \frac{{m\pi y_{{0{\text{D}},g}} }}{{y_{{e{\text{D}}}} }}} \right\} \\ & \quad \cdot \left\{ {1 + 2\sum\limits_{m = 1}^{\infty } {\exp \left[ { - \frac{{m^{2} \pi^{2} \left( {t_{\text{D}}^{n} - t_{\text{D}}^{l - 1} - \tau_{\text{D}} } \right)}}{{z_{{e{\text{D}}}}^{2} }}} \right]\cos \frac{{m\pi z_{{0{\text{D}},k}} }}{{z_{{e{\text{D}}}} }}\cos \frac{{m\pi z_{{0{\text{D}},g}} }}{{z_{{e{\text{D}}}} }}} } \right\}{\text{d}}\tau_{\text{D}} \\ \end{aligned} $$

(B-14)

Moving the unknowns in Eq. (B-13) to the left-hand side, we can have:

$$ p_{{{\text{fD}},g}}^{n} - \sum\limits_{k = 1}^{k = Nf} {q_{{{\text{fD}},k}}^{n} G_{n,k,g} } = p_{{{\text{fD}},g}}^{n - 1} + \left( {\sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n - 1} {q_{{{\text{fD}},k}}^{l} G_{l,k,g} } } - \sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {q_{{{\text{fD}},k}}^{l - 1} G_{l,k,g} } } } \right) $$

(B-15)

As a result, we can formulate the dimensionless pressures of the fractures elements and dimensionless withdrawal rates of the fracture elements into a matrix form:

$$ B \cdot \left[ \begin{aligned} p_{\text{fD}} \hfill \\ q_{\text{fD}} \hfill \\ \end{aligned} \right] = {\text{RHS}}_{2} $$

(B-16)

where

$$ B = \left[ \begin{aligned} \underbrace {{1{ 0 }0{ 0 } \cdots { 0 0}}}_{{N_{\text{f}} }} \, \underbrace {{G_{n,1,1} \, \cdots G_{n,k,1} \cdots \, G_{{n,N_{\text{f}} ,1}} }}_{{N_{\text{f}} }} \hfill \\ \, \vdots \hfill \\ \underbrace {{\overbrace {{0 \, \cdots { 0 }}}^{g - 1}{ 1 0 } \cdots { 0 }}}_{{N_{\text{f}} }} \, \underbrace {{G_{n,1,g} \cdots G_{n,k,g} \cdots \, G_{{n,N_{\text{f}} ,g}} }}_{{N_{\text{f}} }} \hfill \\ \, \vdots \hfill \\ \underbrace {{ 0 { 0 } \cdots { 0 0 0 1}}}_{{N_{\text{f}} }} \, \underbrace {{G_{n,1,Nf} \cdots G_{{n,k,N_{\text{f}} }} \cdots G_{{n,N_{\text{f}} ,N_{\text{f}} }} }}_{{N_{\text{f}} }} \hfill \\ \end{aligned} \right]_{{N_{\text{f}} \times 2N_{\text{f}} }} $$

(B-17)

$$ {\text{RHS}}_{2} = \left[ \begin{aligned} p_{{{\text{fD}},1}}^{n - 1} + \left( {\sum\limits_{k = 1}^{{k = N_{\text{f}} }} {\sum\limits_{l = 1}^{l = n - 1} {q_{{{\text{fD}},k}}^{l} G_{l,k,1} } } - \sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {q_{{{\text{fD}},k}}^{l - 1} G_{l,k,1} } } } \right) \hfill \\ \, \vdots \hfill \\ p_{{{\text{fD}},g}}^{n - 1} + \left( {\sum\limits_{k = 1}^{{k = N_{\text{f}} }} {\sum\limits_{l = 1}^{l = n - 1} {q_{{{\text{fD}},k}}^{l} G_{l,k,g} } } - \sum\limits_{k = 1}^{k = Nf} {\sum\limits_{l = 1}^{l = n} {q_{{{\text{fD}},k}}^{l - 1} G_{l,k,g} } } } \right) \hfill \\ \, \vdots \hfill \\ p_{{{\text{fD}},N_{\text{f}} }}^{n - 1} + \left( {\sum\limits_{k = 1}^{{k = N_{\text{f}} }} {\sum\limits_{l = 1}^{l = n - 1} {q_{{{\text{fD}},k}}^{l} G_{{l,k,N_{\text{f}} }} } } - \sum\limits_{k = 1}^{{k = N_{\text{f}} }} {\sum\limits_{l = 1}^{l = n} {q_{{{\text{fD}},k}}^{l - 1} G_{{l,k,N_{\text{f}} }} } } } \right) \hfill \\ \end{aligned} \right]_{{N_{\text{f}} \times 1}} $$

(B-18)