Skip to main content
SpringerLink
Log in

A Two-Layer Mathematical Model of Blood Flow in Porous Constricted Blood Vessels

  • Published:
Transport in Porous Media Aims and scope Submit manuscript

Abstract

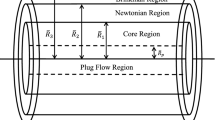
In this paper, we discussed a mathematical model for two-layered non-Newtonian blood flow through porous constricted blood vessels. The core region of blood flow contains the suspension of erythrocytes as non-Newtonian Casson fluid and the peripheral region contains the plasma flow as Newtonian fluid. The wall of porous constricted blood vessel configured as thin transition Brinkman layer over layered by Darcy region. The boundary of fluid layer is defined as stress jump condition of Ocha-Tapiya and Beavers–Joseph. In this paper, we obtained an analytic expression for velocity, flow rate, wall shear stress. The effect of permeability, plasma layer thickness, yield stress and shape of the constriction on velocity in core & peripheral region, wall shear stress and flow rate is discussed graphically. This is found throughout the discussion that permeability and plasma layer thickness have accountable effect on various flow parameters which gives an important observation for diseased blood vessels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Beavers, G.S., Joseph, D.D.: Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30(1), 197–207 (1967)

    Article  Google Scholar 

  • Boodoo, C., Bhatt, B., Comissiong, D.: Two-phase fluid flow in a porous tube: a model for blood flow in capillaries. Rheol. Acta 52(6), 579–588 (2013)

    Article  Google Scholar 

  • Brinkman, H.C.: Experimental data on the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A 1(1), 27–34 (1947)

    Article  Google Scholar 

  • Brinkman, H.C.: On the permeability of media consisting of closely packed porous particles. Appl. Sci. Res. 1(1), 81–86 (1949)

    Article  Google Scholar 

  • Chakravarty, S., Datta, A.: Pulsatile blood flow in a porous stenotic artery. Math. Comput. Modell. 16(2), 35–54 (1992)

    Article  Google Scholar 

  • Dash, R., Mehta, K.: Casson fluid in a pipe filled with a homogeneous porous medium. Int. J. Eng. Sci. 34(10), 1145–1156 (1996)

    Article  Google Scholar 

  • Dash, R.K., Mehta, K.N., Jayaraman, G.: Effect of yield stress on the flow of a Casson fluid in a homogeneous porous medium bounded by a circular tube. Appl. Sci. Res. 57, 133–149 (1997)

    Article  Google Scholar 

  • Ehrhardt, M.: An introduction to fluid-porous interface coupling. Angewandte Mathematik und Numerische Mathematik, 1–10 (2010)

  • Goharzadeh, A., Saidi, A., Wang, D., Merzkirch, W., Khalili, A.: An experimental investigation of the brinkman layer thickness at a fluid-porous interface. In: IUTAM Symposium on One Hundred Years of Boundary Layer Research, pp. 445–454 (2006)

  • Haldar, K., Anderson, H.I.: Two-layered model of blood flow through stenosed arteries. Acta Mech. 117, 221–228 (1996)

    Article  Google Scholar 

  • Hill, A.A., Straughan, B.: Poiseuille flow in a fluid overlying a porous medium. J. Fluid Mech. 603, 137–149 (2008)

    Article  Google Scholar 

  • Khaled, A.R.A., Vafai, K.: The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 46(2003), 4989–5003 (2003)

    Article  Google Scholar 

  • Mckinley, R .M., Jahns, H., Harris, W .W.: Non Newtonian flow in porous media. A.I.Ch.E. J. 12(1), 17–20 (1966)

    Article  Google Scholar 

  • Mehmood, O.U., Mustapha, N., Shafie, S.: Unsteady two-dimensional blood flow in porous artery with multi-irregular stenoses. Transp. Porous Media 92, 259–275 (2012)

    Article  Google Scholar 

  • Misra, J.C., Sinha, A., Shit, G.C.: Mathematical modeling of blood flow in a porous vessel having double stenoses in the presence of an external magnetic field. Int. J. Biomath. 04(02), 207–225 (2011)

    Article  Google Scholar 

  • Muskat, M.: The flow of fluids through porous media. J. Appl. Phys. 8, 274–282 (1937)

    Article  Google Scholar 

  • Nield, D.A.: The boundary correction for the Rayleigh-Darcy problem : limitations of the Brinkman equation. J. Fluid Mech. 128, 37–46 (1983)

    Article  Google Scholar 

  • Ochoa-Tapia, J.A., Whitakeri, S.: Momentum transfer at the boundary between a porous medium and a homogeneous fluid I. Theoretical development. Int. J. Heat Mass Transf. 38(14), 2635–2646 (1995)

    Article  Google Scholar 

  • Odeh, A.S., Yang, H.T.: Flow of non-Newtonian power-law fluids through porous media. Soc. Pet. Eng. AIME 7139(June), 155–163 (1979)

    Article  Google Scholar 

  • Ponalagusamy, R.: Blood flow through an artery with mild stenosis: a two layered model with different shapes of stenosis and slip velocity at wall. J. Appl. Sci. 7(7), 1071–1077 (2007)

    Article  Google Scholar 

  • Ponalagusamy, R., Selvi, T.R.: A study on two-layered model (CassonNewtonian) for blood flow through an arterial stenosis: axially variable slip velocity at the wall. J. Frankl. Inst. 348, 2308–2321 (2011)

    Article  Google Scholar 

  • Pries, A.R., Secomb, T.W., Gaehtgens, P.: Biophysical aspects of blood flow in the microvasculature. Cardiovasc. Res. 32(1996), 654–667 (1996)

    Article  Google Scholar 

  • Sacheti, N.C., Chandran, P., Khod, A., Oman, S.: Steady creeping motion of a liquid bubble in an immiscible viscous fluid bounded by a vertical porous cylinder of finite thickness. Adv. Stud. Theor. Phys. 2(5), 243–260 (2008)

    Google Scholar 

  • Sankar, D., Lee, U.: Two-fluid Casson model for pulsatile blood flow through stenosed arteries: a theoretical model. Commun. Nonlinear Sci. Numer. Simul. 15(2010), 2086–2097 (2010)

    Article  Google Scholar 

  • Sankar, D.S.: A two-fluid model for pulsatile flow in catheterized blood vessels. Int. J. Non Linear Mech. 44(4), 337–351 (2009)

    Article  Google Scholar 

  • Shivakumar, P.N., Nagaraj, S., Veerabhadraiah, R., Rudraiah, N.: Fluid movement in a channel of varying gap with permeable walls covered by porous media. Int. J. Eng. Sci. 24(4), 479–492 (1986)

    Article  Google Scholar 

  • Shukla, J.B., Parihar, R.S., Gupta, S.P.: Effect of peripheral layer viscosity on blood flow through the artery with mild stenosis. Bull. Math. Biol. 42, 797–805 (1980)

    Article  Google Scholar 

  • Sochi, T.: Non-Newtonian flow in porous media. Polymer 51(22), 5007–5023 (2010)

    Article  Google Scholar 

  • Srivastava, V.P., Saxena, M.: Two-layered model of Casson fluid flow through stenotic blood vessels- application to the cardiovascular system. J. Biomech. 27(7), 921–928 (1994)

    Article  Google Scholar 

  • Straughan, B.: Stability and Wave Motion in Porous Media, vol. 165, 165th edn. Springer, New York (2008)

    Google Scholar 

  • Tang, H.T., Fung, Y.C.: Fluid movement in a channel With permeable walls covered by porous media: a model of lung alveolar sheet. J. Appl. Mech. 42(March), 45–50 (1975)

    Article  Google Scholar 

  • Whitaker, S.: Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1(1), 3–25 (1986)

    Article  Google Scholar 

Download references

Acknowledgements

Bhupesh Dutt Sharma was supported by the MHRD Fellowship for Research Scholars administered by MNNIT Allahabad.

Author information

Authors and Affiliations

  1. Department of Mathematics, Motilal Nehru National Institute of Technology Allahabad, Allahabad, 211004, India

    Bhupesh Dutt Sharma & Pramod Kumar Yadav

Authors
  1. Bhupesh Dutt Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pramod Kumar Yadav
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bhupesh Dutt Sharma.

Appendix A

Appendix A

$$\begin{aligned} v_1&= -8 \sqrt{2} \sqrt{P \theta } (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2\\&\quad +\, \beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )- (\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_1^{3/2} \\&\quad + 3 P (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+ \beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )\\&\quad - (\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) (\lambda _1-1) R_1^2-12 \theta (\alpha I_0\left( \gamma R_3\right) \\&\quad (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) \\&\quad - \sqrt{k} \gamma I_1\left( \gamma R_2\right) )(\alpha K_0\left( \gamma R_3\right) +\gamma K_1 (\gamma R_3) \sqrt{k})) R_1+r (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k}) \\&\quad - I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )- (\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) \\&\quad + \gamma K_1\left( \gamma R_3\right) \sqrt{k})) (3 P r+12 \theta -8 \sqrt{2} \sqrt{r} \sqrt{P \theta })-3 P (4 \gamma ((\alpha I_0\left( \gamma R_3\right) -\sqrt{k} \gamma I_1\left( \gamma R_3\right) ) K_1\left( \gamma R_2\right) \\&\quad + I_1\left( \gamma R_2\right) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) k^{3/2}+ (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})\\&\quad - I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) \\&\quad + \gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_2^2-2 \sqrt{k} \phi (-\alpha I_0\left( \gamma R_3\right) K_0\left( \gamma R_2\right) +\gamma I_1\left( \gamma R_3\right) \sqrt{k} K_0\left( \gamma R_2\right) +I_0\left( \gamma R_2\right) \\&\quad (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_2) \lambda _1 \div 12 (\alpha I_0\left( \gamma R_3\right) \left( \beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k}\right) \\&\quad -I_1\left( \gamma R_3\right) \left( k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma \right) -\left( \beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) \right) (\alpha K_0\left( \gamma R_3\right) . \\&\quad +\gamma K_1\left( \gamma R_3) \sqrt{k}\right) ) \lambda _1\\ v_2&= \frac{1}{4} P \bigg (-4 \gamma k^{3/2} \left( K_1\left( \gamma R_2\right) \left( \alpha I_0\left( \gamma R_3\right) -\gamma \sqrt{k} I_1\left( \gamma R_3\right) \right) +I_1\left( \gamma R_2\right) \left( \gamma \sqrt{k} K_1\left( \gamma R_3\right) +\alpha K_0\left( \gamma R_3\right) \right) \right) \\&\quad +R_2^2 (-\alpha I_0\left( \gamma R_3\right) \left( \gamma \sqrt{k} K_1\left( \gamma R_2\right) +\beta \phi K_0\left( \gamma R_2\right) \right) +\left( \gamma \sqrt{k} K_1\left( \gamma R_3\right) +\alpha K_0\left( \gamma R_3\right) \right) (\beta \phi I_0\left( \gamma R_2\right) \\&\quad -\gamma \sqrt{k} I_1\left( \gamma R_2\right) )+I_1\left( \gamma R_3\right) \left( \beta \gamma \sqrt{k} \phi K_0\left( \gamma R_2\right) +\gamma ^2 k K_1\left( \gamma R_2\right) \right) )+ 2 \sqrt{k} R_2 \phi (I_0\left( \gamma R_2\right) \\&\quad \left( \gamma \sqrt{k} K_1\left( \gamma R_3\right) +\alpha K_0\left( \gamma R_3\right) \right) +\gamma \sqrt{k} I_1\left( \gamma R_3\right) K_0\left( \gamma R_2\right) -\alpha I_0\left( \gamma R_3\right) K_0\left( \gamma R_2\right) ) \div \alpha I_0\left( \gamma R_3\right) \\&\quad \left( \gamma \sqrt{k} K_1\left( \gamma R_2\right) +\beta \phi K_0\left( \gamma R_2\right) \right) -\left( \gamma \sqrt{k} K_1\left( \gamma R_3\right) +\alpha K_0\left( \gamma R_3\right) \right) \left( \beta \phi I_0\left( \gamma R_2\right) -\gamma \sqrt{k} I_1\left( \gamma R_2\right) \right) \\&-I_1\left( \gamma R_3\right) \left( \beta \gamma \sqrt{k} \phi K_0\left( \gamma R_2\right) +\gamma ^2 k K_1\left( \gamma R_2\right) \right) +r^2).\\ v_3&=( \sqrt{k} P (2 (\alpha \left( -\sqrt{k}\right) I_0\left( \gamma R_3\right) \left( \gamma \sqrt{k} K_1\left( \gamma R_2\right) -\beta \phi K_0(r \gamma )+\beta \phi K_0\left( \gamma R_2\right) \right) -\sqrt{k} (\gamma \sqrt{k} K_1\left( \gamma R_3\right) \\&\quad +\alpha K_0\left( \gamma R_3\right) ) \left( \gamma \sqrt{k} I_1\left( \gamma R_2\right) +\beta \phi I_0(r \gamma )-\beta \phi I_0\left( \gamma R_2\right) \right) +\gamma k I_1\left( \gamma R_3\right) (\gamma \sqrt{k} K_1\left( \gamma R_2\right) -\beta \phi K_0(r \gamma )\\&\quad +\beta \phi K_0\left( \gamma R_2\right) )) +R_2 \phi (I_0(r \gamma ) \left( \gamma \sqrt{k} K_1\left( \gamma R_3\right) +\alpha K_0\left( \gamma R_3\right) \right) +\gamma \sqrt{k} K_0(r \gamma ) I_1\left( \gamma R_3\right) -\alpha K_0(r \gamma )\\&\quad I_0\left( \gamma R_3\right) ))) \div 2 (\alpha I_0\left( \gamma R_3\right) \left( \gamma \sqrt{k} K_1\left( \gamma R_2\right) +\beta \phi K_0\left( \gamma R_2\right) \right) -\left( \gamma \sqrt{k} K_1\left( \gamma R_3\right) +\alpha K_0\left( \gamma R_3\right) \right) \\&\quad \left( \beta \phi I_0\left( \gamma R_2\right) -\gamma \sqrt{k} I_1\left( \gamma R_2\right) \right) -I_1\left( \gamma R_3\right) \left( \beta \gamma \sqrt{k} \phi K_0\left( \gamma R_2\right) +\gamma ^2 k K_1\left( \gamma R_2\right) \right) \bigg ).\\ Q&= - 176 (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )\\&\quad -(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) \sqrt{2} \sqrt{P \theta } R_1^{7/2}-21 P (\alpha I_0\left( \gamma R_3\right) \\&\quad (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) \\&\quad -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k}))(2 \lambda _1-1) R_1^4+56 \theta (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) \\&\quad +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) )\\&\quad (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_1^3+21 P (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) \\&\quad (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k}))\\&\quad \lambda _1 R_1^2+21 P (2 (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \\&\quad \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_2^4-4 \sqrt{k} \phi (-\alpha I_0\left( \gamma R_3\right) \\&\quad K_0\left( \gamma R_2\right) +\gamma I_1\left( \gamma R_3\right) \sqrt{k} K_0\left( \gamma R_2\right) +I_0\left( \gamma R_2\right) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_2^3+(-\alpha I_0\left( \gamma R_3\right) \\&\quad ((8 k+1) \beta \phi K_0\left( \gamma R_2\right) +\gamma (1-8 \phi ) K_1\left( \gamma R_2\right) \sqrt{k})+\gamma I_1\left( \gamma R_3\right) \sqrt{k} ((8 k+1) \beta \phi K_0\left( \gamma R_2\right) +\gamma (1-8 \phi )\\&\quad K_1\left( \gamma R_2\right) \sqrt{k})+((8 k+1) \beta \phi I_0\left( \gamma R_2\right) +\gamma (8 \phi -1) I_1\left( \gamma R_2\right) \sqrt{k}) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_2^2 \\&\quad -8 \sqrt{k} \gamma \phi (2 (I_1\left( \gamma R_2\right) (k \beta \gamma K_1\left( \gamma R_3\right) {+}\alpha \beta K_0\left( \gamma R_3\right) \sqrt{k}){+}\beta (\alpha I_0\left( \gamma R_3\right) -\sqrt{k} \gamma I_1\left( \gamma R_3\right) ) K_1\left( \gamma R_2\right) \sqrt{k}) \\&\quad +\alpha (I_1\left( \gamma R_3\right) K_0\left( \gamma R_3\right) +I_0\left( \gamma R_3\right) K_1\left( \gamma R_3\right) ) R_3) R_2-8 k (-2 (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \\&\quad \sqrt{k})-I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) \\&\quad + \gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_3^2{-}2 \alpha \beta \gamma \phi (I_1\left( \gamma R_3\right) K_0\left( \gamma R_3\right) {+}I_0\left( \gamma R_3\right) K_1\left( \gamma R_3\right) ) R_3{+}(\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) \\&\quad +\gamma K_1\left( \gamma R_2\right) \sqrt{k}){-}I_1\left( \gamma R_3\right) (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma ){-}(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) )\\&\quad (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) R_4^2)) \lambda _1 \div 336 (\alpha I_0\left( \gamma R_3\right) (\beta \phi K_0\left( \gamma R_2\right) +\gamma K_1\left( \gamma R_2\right) \sqrt{k})-I_1\left( \gamma R_3\right) \\&\quad (k K_1\left( \gamma R_2\right) \gamma ^2+\beta \phi K_0\left( \gamma R_2\right) \sqrt{k} \gamma )-(\beta \phi I_0\left( \gamma R_2\right) -\sqrt{k} \gamma I_1\left( \gamma R_2\right) ) (\alpha K_0\left( \gamma R_3\right) +\gamma K_1\left( \gamma R_3\right) \sqrt{k})) \lambda _1 \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, B.D., Yadav, P.K. A Two-Layer Mathematical Model of Blood Flow in Porous Constricted Blood Vessels. Transp Porous Med 120, 239–254 (2017). https://doi.org/10.1007/s11242-017-0918-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11242-017-0918-9

Keywords

Search

Navigation