Abstract
The momentum transfer between a homogeneous fluid and a porous medium in a system analogous to the one used by Beavers and Joseph (J Fluid Mech 30:197–207, 1967) is studied using volume averaging techniques. In this article, we present a closed generalized momentum transport equation (GTE) that is valid everywhere and is expressed in terms of position-dependent effective transport coefficients, which are computed from the solution of associated closure problems previously reported. A combination of the velocity profiles from the GTE in the definition of the excess terms that define the jump coefficients allows their computation using numerical techniques. The calculations are in concordance with those resulting from the work of Goyeau et al. (Int J Heat Mass Transf. 46:4071–4081, 2003), showing a strong dependence with the porosity. In addition, the effects of the roughness of the boundary on the computation of the position-dependent permeability tensor in the inter-region are also analyzed.
Similar content being viewed by others
Abbreviations
- \({\fancyscript{A}_{\eta \omega}}\) :
-
Area of the inter-region (m2)
- A j :
-
Surface of the j-region contained within the superficial area of V ∞, j = ω, η
- A βσ :
-
Interfacial surface contained within the averaging volume
- \({\left\langle {\textsf{\textbf{B}}_\beta}\right\rangle_s}\) :
-
Brinkman stress tensor (N/m2)
- b β :
-
Vector field that maps \({\mu_\beta \left\langle {{\bf v}_\beta}\right \rangle^{\beta}}\) onto \({\tilde {p}_\beta}\) (m−1)
- \({\textsf{\textbf{C}}_\beta}\) :
-
Second-order tensor field that maps \({\left\langle {{\bf v}_\beta}\right\rangle^\beta}\) onto (\({{\tilde{\bf v}}_\beta}\))
- g :
-
Gravity vector (m/s2)
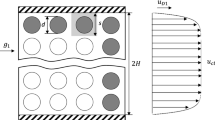
- H :
-
Distance from the dividing surface to the lower wall (m)
- h :
-
Distance from the dividing surface to the upper wall (m)
- \({\textsf{\textbf{I}}}\) :
-
Identity tensor
- \({\textsf{\textbf{K}}_\beta}\) :
-
Permeability tensor valid everywhere (m2)
- \({{K}_\beta^{-1}}\) :
-
Tangential component of the global stress tensor valid everywhere (m2)
- \({\textsf{\textbf{K}}_{\beta \omega}}\) :
-
Darcy’s law permeability tensor in the ω-region (m2)
- K βω :
-
Norm of Darcy’s law permeability tensor in the ω-region (m2)
- l i :
-
Lattice vectors of the unit cell (i = 1, 2) (m)
- l j :
-
Characteristic length for the j-phase; j = β, σ (m)
- L :
-
Characteristic length associated with volume averaged quantities (m)
- L v :
-
Characteristic length associated with \({\left. {\left\langle {{\bf v}_\beta}\right\rangle}\right|_{\bf x}}\) (m)
- L v1 :
-
Characteristic length associated with \({\nabla \left. {\left\langle {{\bf v}_\beta}\right\rangle}\right|_{\bf x}}\) (m)
- n βσ :
-
Unit normal vector directed from the β-phase toward the σ-phase
- n ηω :
-
Unit normal vector directed from the η-region toward the ω-region
- p β :
-
Pressure in the β-phase (N/m2)
- \({\left\langle{p_\beta}\right\rangle^\beta}\) :
-
Intrinsic average pressure (N/m2)
- \({\left\langle {p_\beta}\right\rangle_{j}^\beta}\) :
-
Intrinsic average pressure in the j-region; j = ω, η (N/m2)
- r :
-
Position vector (m)
- r 0 :
-
Radius of the averaging volume (m)
- \({\left\langle \textsf{\textbf{T}}\right\rangle_s}\) :
-
Surface stress (N/m2)
- \({\left\langle {\textsf{\textbf{T}}_\beta}\right\rangle_s}\) :
-
Bulk stress tensor (N/m2)
- \({\fancyscript{V}_{j}}\) :
-
Volume of the j-phase contained within the local averaging volume, j = β, σ (m3)
- V :
-
averaging region
- \({\fancyscript{V}}\) :
-
Local averaging volume (m3)
- v β :
-
Velocity vector in the β-phase (m/s)
- \({\left\langle{{\bf v}_\beta}\right\rangle}\) :
-
Superficial average velocity vector (m/s)
- \({\left\langle {{\bf v}_\beta}\right\rangle_{j}}\) :
-
Superficial average velocity vector in the j-region; j = ω, η (m/s)
- \({\left\langle {v_\beta}\right\rangle_{j}}\) :
-
Tangential component of \({\left\langle{{\bf v}_\beta}\right\rangle_{j}}\) ; j = ω, η (m/s)
- x :
-
Position vector locating the centroid of the averaging volume (m)
- y β :
-
Position vector relative to the centroid of the averaging volume V (m)
- δ :
-
Half of the height of the unit cell (m)
- ε β (x):
-
Position-dependent volume fraction of the β-phase
- ε βω :
-
Volume fraction of the β-phase in the ω-region
- \({\phi }\) :
-
Jump coefficient associated with superficial effects
- η :
-
Roughness factor
- μ β :
-
Viscosity of the β-phase (Ns/m2)
- \({\nabla_s}\) :
-
\({\left({\textsf{\textbf{I}}-{\bf n}_{\eta \omega} {\bf n}_{\eta \omega}}\right)\cdot \nabla}\) Surface gradient operator
- ρ β :
-
Density of the β-phase (kg/m3)
- η :
-
Relative to the η-region
- ω :
-
Relative to the ω-region
- 0, s, b :
-
Relative to the dividing surface
- K :
-
Relative to the permeability
- GTE:
-
Generalized transport equations
- ODA:
-
One-domain approach
- TDA:
-
Two-domain approach
References
Aspa, Y.: Modélisation de l’ablation des composites C/C dans les Tuyères. PhD Thesis, Institut National Polytechnique de Toulouse, France (2006)
Beavers G.S., Joseph D.D.: Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207 (1967). doi:10.1017/S0022112067001375
Bird R.B., Stewart W.E., Lightfoot E.N.: Transport Phenomena, 2nd edn. Wiley, New York (2002)
Breugem, P.W.: The influence of wall permeability on laminar and turbulent flows. PhD Thesis, Delft University, The Netherlands (2005)
Chandesris M., Jamet D.: Boundary conditions at a planar fluid–porous interface for a Poiseuille flow. Int. J. Heat Mass Transf. 49, 2137–2150 (2006). doi:10.1016/j.ijheatmasstransfer.2005.12.010
Chandesris M., Jamet D.: Boundary conditions at a fluid–porous interface: An a priori estimation of the stress jump coefficients. Int. J. Heat Mass Transf. 50, 3422–3436 (2007). doi:10.1016/j.ijheatmasstransfer.2007.01.053
Cieszko M., Kubik J.: Derivation of matching conditions at the contact surface between fluid-saturated porous solid and bulk fluid. Transp. Porous Media 34, 319–336 (1999). doi:10.1023/A:1006590215455
Goharzadeh A., Khalili A., Jørgensen B.B.: Transition layer thickness at a fluid–porous interface. Phys. Fluids 17, 057102 (2005). doi:10.1063/1.1894796
Goyeau B., Lhuillier D., Gobin D., Velarde M.G.: Momentum transport at a fluid–porous interface. Int. J. Heat Mass Transf. 46, 4071–4081 (2003). doi:10.1016/S0017-9310(03)00241-2
Kubik J., Cieszko M.: Analysis of matching conditions at the boundary surface of a fluid-saturated porous solid and a bulk fluid: The use of Lagrange multipliers. Contin. Mech. Thermodyn. 17, 351–359 (2005). doi:10.1007/s00161-005-0001-6
Morales-Zárate E., Valdés-Parada F.J., Goyeau B., Ochoa-Tapia J.A.: Diffusion and reaction in three-phase systems: Average transport equations and jump boundary conditions. Chem. Eng. J. 138, 307–332 (2008). doi:10.1016/j.cej.2007.05.054
Neale G., Nader W.: Practical significance of Brinkman’s extension of Darcy’s law: Coupled parallel flows within a channel and a bounding porous medium. Can. J. Chem. Eng. 52, 475–478 (1974)
Ochoa-Tapia J.A., Whitaker S.: Momentum transfer at the boundary between a porous medium and a homogeneous fluid-I: Theoretical development. Int. J. Heat Mass Transf. 38(14), 2635–2646 (1995a). doi:10.1016/0017-9310(94)00346-W
Ochoa-Tapia J.A., Whitaker S.: Momentum transfer at the boundary between a porous medium and a homogeneous fluid-II: Comparison with experiment. Int. J. Heat Mass Transf. 38(14), 2647–2655 (1995b). doi:10.1016/0017-9310(94)00347-X
Ochoa-Tapia J.A., Whitaker S.: Momentum jump condition at the boundary between a porous medium and a homogenous fluid: Inertial effects. J. Porous Media 1, 201–207 (1998)
Poulikakos D., Kazmierczac M.: Forced convection in a duct partially filled with a porous material. J. Heat Transf. 109, 653–662 (1987)
Prat M.: On the boundary conditions at the macroscopic level. Transp. Porous Media 4, 259–280 (1989). doi:10.1007/BF00138039
Prat M.: Modeling of heat transfer by conduction in a transition region between a porous medium and an external fluid. Transp. Porous Media 5, 71–95 (1990). doi:10.1007/BF00714629
Prat M.: Some refinements concerning the boundary conditions at the macroscopic level. Transp. Porous Media 7, 147–161 (1992). doi:10.1007/BF00647394
Sahraoui M., Kaviany M.: Slip and no-slip temperature boundary conditions at the interface of porous plain media: Conduction. Int. J. Heat Mass Transf. 36, 1019–1033 (1993). doi:10.1016/S0017-9310(05)80286-8
Vafai K., Kim S.J.: Fluid mechanics of the interface region between a porous medium and a fluid layer—An exact solution. Int. J. Heat Fluid Flow 11, 254–256 (1990). doi:10.1016/0142-727X(90)90045-D
Valdés-Parada F.J., Goyeau B., Ochoa-Tapia J.A.: Diffusive mass transfer between a microporous medium and an homogeneous fluid: Jump boundary conditions. Chem. Eng. Sci. 61, 1692–1704 (2006). doi:10.1016/j.ces.2005.10.005
Valdés-Parada F.J., Goyeau B., Ochoa-Tapia J.A.: Jump momentum boundary condition at a fluid–porous dividing surface: Derivation of the closure problem. Chem. Eng. Sci. 62, 4025–4039 (2007a). doi:10.1016/j.ces.2007.04.042
Valdés-Parada F.J., Ochoa-Tapia J.A., Alvarez-Ramirez J.: Diffusive mass transport in fluid–porous medium inter-region: Closure problem solution for the one-domain approach. Chem. Eng. Sci. 62, 6054–6068 (2007b). doi:10.1016/j.ces.2007.06.012
Valencia-López J.J., Espinosa Paredes G., Ochoa-Tapia J.A.: Mass transfer jump condition at the boundary between a porous medium and a homogeneous fluid. J. Porous Media 6, 33–49 (2003). doi:10.1615/JPorMedia.v6.i1.20
Whitaker S.: The method of volume averaging. Kluwer, Dordrecht (1999)
Wood B.D., Quintard M., Whitaker S.: Jump condition at non-uniform boundaries: The catalytic surface. Chem. Eng. Sci. 55, 5231–5245 (2000). doi:10.1016/S0009-2509(00)00161-5
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Valdés-Parada, F.J., Alvarez-Ramírez, J., Goyeau, B. et al. Computation of Jump Coefficients for Momentum Transfer Between a Porous Medium and a Fluid Using a Closed Generalized Transfer Equation. Transp Porous Med 78, 439–457 (2009). https://doi.org/10.1007/s11242-009-9370-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-009-9370-9