Skip to main content
SpringerLink
Log in

One-dimensional unsteady inertial flow in phreatic aquifers induced by a sudden change of the boundary head

  • Original Paper
  • Published:
Transport in Porous Media Aims and scope Submit manuscript

Abstract

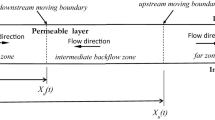
We are examining the classical problem of unsteady flow in a phreatic semi-infinite aquifer, induced by sudden rise or drawdown of the boundary head, by taking into account the influence of the inertial effects. We demonstrate that for short times the inertial effects are dominant and the equation system describing the flow behavior can be reduced to a single ordinary differential equation. This equation is solved both numerically by the Runge-Kutta method and analytically by the Adomian’s decomposition approach and an adequate polynomial-exponential approximation as well. The influence of the viscous term, occurring for longer times, is also taken into account by solving the full Forchheimer equation by a finite difference approach. It is also demonstrated that as for the Darcian flow, for the case of small fluctuations of the water table, the computation procedure can be simplified by using a linearized form of the mass balance equation. Compact analytical expressions for the computation of the water stored or extracted from an aquifer, including viscous corrections are also developed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Adomian G. (1990). Solving Frontier Problems in Physics—The Decomposition Method. Kluwer Academic Publishers, Dordrecht, 352

    Google Scholar 

  • Barry D.A., Parlange J.-Y., Hogarth W.L., Govindaraju R.S., Parlange M.B., Lockington D. and Li L. (2000). Comment on Modeling transient stream/aquifer interaction with the non-linear Boussinesq equation and its analytical solution by Serrano, SE, Workman, SR, 1998. J. Hydrol. 235: 289–292

    Article  Google Scholar 

  • Bear J. (1972). Dynamics of Fluids in Porous Media. Dover, New York, 764

    Google Scholar 

  • Bear J. (1979). Hydraulics of Groundwater. Mc-Graw Hill, New York, 567

    Google Scholar 

  • Burcharth H.F. and Anderson O.H. (1995). On the one-dimensional steady and unsteady porous flow equations. Coast. Eng. 24: 233–257

    Article  Google Scholar 

  • Chen Z.-H., Bodvarsson G.S., Whitherspoon P.A. and Yortsos Y.C. (1995). An integral equation formulation for the unconfined flow of groundwater with variable inlet conditions. Trans. Porous Media 18: 15–36

    Article  Google Scholar 

  • Chu W.-S. and Willis R. (1984). An explicit finite difference model for unconfined aquifers. Ground 22(6): 728–734

    Article  Google Scholar 

  • Crank J. (1975). The Mathematics of Diffusion. Clarendon, Oxford, 462

    Google Scholar 

  • Fourar M., Radilla G., Lenormand R. and Moyne C. (2004). On the non-linear behavior of a laminar single phase flow through two and three-dimensional porous media. Adv. Water Resour. 27: 669–677

    Article  Google Scholar 

  • Fourar M., Lenormand R., Karimi-Fard M. and Horne R. (2005). Inertia effects in high-rate flow through heterogeneous porous media. Trans. Porous Media 60: 353–370

    Article  Google Scholar 

  • Guo W. (1997). Transient groundwater flow between reservoirs and water-table aquifers. J. Hydrol. 195: 370–384

    Article  Google Scholar 

  • Greenly B.T. and Joy D.M. (1996). One-dimensional finite-element mofel for high flow velocities in porous media. J. Geotech. Engng. 122: 789–796

    Article  Google Scholar 

  • Hogarth W.L. and Parlange J.-Y. (1999). Solving the Boussinesq equation using solutions of the Blasius equation. Water Resour. Res. 35(3): 885–887

    Article  Google Scholar 

  • Hsu C.T. and Cheng P. (1990). Thermal dispersion in a porous medium. Int. J. Heat Mass Trans. 33: 1587–1597

    Article  Google Scholar 

  • Kacimov A.R. (2000). Three dimensional groundwater flow to a lake: an explicit solution. J. Hydrol. 240: 80–89

    Article  Google Scholar 

  • Li L., Barry D.A., Stagnitti F., Parlange J.-Y. and Jeng D.S. (2000). Beach water fluctuations due to spring-neap tides: moving boundary effects. Adv Water. Resour. 23: 817–824

    Article  Google Scholar 

  • Li L., Barry D.A., Stagnitti F., Parlange J.-Y. and Jeng D.S. (2002). Reply to S.E. Serrano’s comment on Beach water fluctuations due to spring-neap tides: moving boundary effects. Adv. Water Resour. 25: 586–588

    Google Scholar 

  • Liao S. (2004). Beyond Perturbation. Introduction to the homotopy analysis method. Chapman and Hall, Boca Raton, 322

    Google Scholar 

  • Lockington D.A. (1997). Response of unconfined aquifer to sudden change in boundary head. J. Irrig. Drainage Eng. 123: 24–27

    Article  Google Scholar 

  • Lockington D.A., Parlange J.-Y., Parlange M.B. and Selker J. (2000). Similarity Solution of the Boussinesq equation. Adv. Water Resour. 23: 725–729

    Article  Google Scholar 

  • Jeng D.-S., Seymour B.R., Barry D.A., Parlange J.-Y., Lockington D.A. and Li L. (2005). Steepness expansion for free surface flows in coastal aquifers. J. Hydrol. 309: 85–92

    Article  Google Scholar 

  • McDonald M.G., Harbaugh A.W.: A modular three dimensional finite difference ground-water flow model. US Geological Survey Techniques of Water-Resources Investigations, pp. 596 (1988)

  • Moutsopoulos K.N. and Koch D.L. (1999). Hydrodynamic and boundary-layer dispersion in bidisperse porous media. J. Fluid Mech. 385: 359–379

    Article  Google Scholar 

  • Moutsopoulos K.N. and Tsihrintzis V.A. (2005). Approximate analytical solutions of the Forchheimer equation. J. Hydrol. 309: 93–103

    Article  Google Scholar 

  • Nield D.A. (2000). Resolution of a paradox involving viscous dissipation and nonlinear drag in a porous medium. Trans. Porous Media 41: 349–357

    Article  Google Scholar 

  • Nield D.A. (2002). Modelling fluid flow in saturated porous media and at interfaces. In: Ingham, D.B. and Pop, I. (eds) Transport Phenomena in Porous Media II., pp 1–19. Pergamon, Amsterdam

    Google Scholar 

  • Panfilov M., Oltean C., Panfilova I. and Bues M. (2003). Singular nature of nonlinear macroscale effects in high-rate flow through porous media. C. R. Acad. Sci. Paris Ser. Mecanique 331: 41–48

    Google Scholar 

  • Parlange J.-Y., Hogarth W.L., Govindaraju R.S., Parlange M.B. and Lockington D. (2000). On an exact analytical solution of the Boussinesq equation. Trans. Porous Media 39: 339–345

    Article  Google Scholar 

  • Reddy N.B.P and Rao P.R.M (2006). Effect of convergence on nonlinear flow in porous media. J. Hydraulic Eng. 132: 420–427

    Article  Google Scholar 

  • Sangani A.S. and Behl S. (1989). The planar singular solutions of Stokes and Laplace equations and their application to transport near porous surfaces. Phys. Fluids A 1(1): 21–37

    Article  Google Scholar 

  • Serrano S.E. and Workman S.R. (1998). Modeling transient stream/aquifer interaction with the non-linear Boussinesq equation and its analytical solution. J. Hydrol. 206: 245–255

    Article  Google Scholar 

  • Sidiropoulou, M.G., Moutsopoulos, K.N., Tsihrintzis, V.A.: Determination of coefficients a and b of the Forchheimer equation. Hydrol. Proces., (2006) DOI 10.1002/hyp.6264

  • Sorek S., Levi-Hevroni D., Levy A. and Ben Dor G. (2005). Extensions to the macoscopic Navier–Stokes equation. Trans. Porous Media 61: 215–233

    Article  Google Scholar 

  • Szilagyi J. and Parlange M.B. (1998). Baseflow separation based on analytical solutions of the Boussinesq equation. J. Hydrol. 204: 251–260

    Article  Google Scholar 

  • Telyakovskiy A.S., Braga G. and Furtado F. (2002). Approximate similarity solutions to the Boussinesq equation. Adv. Water Resour. 25: 191–194

    Article  Google Scholar 

  • Terzidis, G.: Steady non-Darcian groundwater flow in unconfined aquifers. In: Proceedings of the 9th Conference of the Hellenic Hydrotechnical Society, Thessaloniki, Greece, April 6-8, pp. 369–389 (2003) (In Greek)

  • Thauvin P. and Mohanty K.K. (1998). Network modeling of non-darcy flow through porous media. Trans. Porous Media 31: 19–37

    Article  Google Scholar 

  • Thiruvengadam M. and Kumar G.N.P (1997). Validity of Forchheimer equation in radial flow coarse granular media. J. Engn. Mech. 123(7): 696–705

    Article  Google Scholar 

  • Tolikas P.K., Sidiropoulos E.G. and Tzimopoulos C.D. (1984). A simple analytical solution for the Boussinesq one-dimensional groundwater flow equation. Water Resour. Res. 20(1): 24–28

    Article  Google Scholar 

  • Venkataraman P. and Rao P.R.M. (1998). Darcian, transitional and turbulent flow through porous media. J. Hydraulic Eng. (ASCE) 124: 840–846

    Article  Google Scholar 

  • Wu Y.S. (2002). Numerical simulation of single-phase and multiphase non-darcy flow in porous and fractured reservoirs. Trans. Porous Media 49: 209–240

    Article  Google Scholar 

  • Zeng Z. and Grigg R. (2006). A Criterion for non-darcy flow in porous media. Trans. Porous Media 63: 57–69

    Article  Google Scholar 

  • Zhang D. (2002). Stochastic Methods for Flow in Porous Media. Academic Press, San Diego, 350

    Google Scholar 

  • Zissis, T., Terzidis, G.: Unsteady non-darcy flow in fractured aquifers. In: Proceedings of the European Conference Advances in Water Technology, 20–23, March, Athens, Greece, pp. 185–194 (1991)

Download references

Author information

Authors and Affiliations

  1. Laboratory of Ecological Engineering and Technology, Department of Environmental Engineering, School of Engineering, Democritus University of Thrace, 67100, Xanthi, Greece

    Konstadinos N. Moutsopoulos

Authors
  1. Konstadinos N. Moutsopoulos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Konstadinos N. Moutsopoulos.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Moutsopoulos, K.N. One-dimensional unsteady inertial flow in phreatic aquifers induced by a sudden change of the boundary head. Transp Porous Med 70, 97–125 (2007). https://doi.org/10.1007/s11242-006-9086-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11242-006-9086-z

Keywords

Search

Navigation