Skip to main content
SpringerLink
Log in

Consistent inconsistencies? Evidence from decision under risk

  • Published:
Theory and Decision Aims and scope Submit manuscript

Abstract

Conventional economic theory assumes that agents should be consistent across decisions. However, it is often observed that experimental subjects fail to report consistent preferences. So far, these inconsistencies are almost always examined singly. We thus wonder whether the more inconsistent individuals in one task are also more inconsistent in other tasks. We propose an experiment in which subjects are asked to report their preferences over risky bets so as to obtain, for each subject, three measures of inconsistencies: classical preference reversals, framing effects and preference instability. In line with previous experimental findings, subjects are largely inconsistent according to each of these three measures and there are considerable individual differences. The main result is that we find no correlation among these three measures of inconsistency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. To illustrate, consider the following bets (source Lichtenstein and Slovic 1971, Table 3): $-bet = ($16, 11/36; \(-\)$1.50, 25/36) and P-bet = ($4, 35/36; \(-\)$1, 1/36). Here, the $-bet offers an 11/36 chance of winning $16 and a 25/36 chance of losing $1.50, while the P-bet offers a 35/36 chance of winning $4 and a 1/36 chance of losing $1. Both bets have an expected value of approximately $3.85.

  2. Cf experiment 1 (with incentives) where 91 choices out of 273 were inconsistent with the announced selling prices (overall preference reversals), 69 out of the 99 choices of the P-bet were inconsistent with the announced selling prices (standard preference reversals) and 22 out of the 174 choices of the $-bet were inconsistent with the selling prices (non-standard preference reversals).

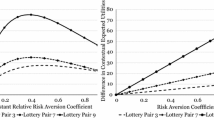
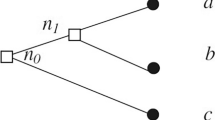
  3. Lottery \({{\mathrm{P}}}^{k}=(x^{k}_{{{\mathrm{P}}}}, p^{k}_{{{\mathrm{P}}}})\) offers €\(x^{k}_{{{\mathrm{P}}}}\) with probability \(p^{k}_{{{\mathrm{P}}}}\), and lottery \(\$^{k}=(x^{k}_{\$} ,p^{k}_{\$})\) offers €\(x^{k}_{\$}\) with probability \(p^{k}_{\$}\).

  4. Following De Martino et al. (2006), we use the questions of set 2 to ensure that subjects remain engaged in the tasks and do not respond randomly throughout this part and also to separate rounds 1 and 3. Some descriptive results for set 2 are presented in the “Appendix”.

  5. Consistent with De Martino et al’s (2006) results, a framing effect was also found across the four probabilities and the four starting amounts used here (see Figs. 15, 16, 17, 18, 19, 20 in the “Appendix”).

  6. We find that 13 subjects out of 41 exhibit a counter-framing effect in round 1, 12 out of 41 in round 3, and 14 out of 41 when we consider all of the observations in set 1 (rounds 1 and 3 together).

  7. For subject i, SFE\(^{i}_{j}\) and NSFE\(^{i}_{j}\) are based on the number of paired-choices in round j (16 when we consider rounds 1 and 3 separately and 32 when we aggregate rounds 1 and 3).

  8. Although 21 % of subjects are not consistent with the predictions of prospect theory, the proportion of standard framing effect is significantly higher than that of non-standard framing effect at better than the 1 % level in set 1. We obtain the same result if we consider the observations in rounds 1 and 3 as separate or not.

References

  • Ameriks, J., Caplin, A., & Leahy, J. (2003). Wealth accumulation and the propensity to plan. The Quarterly Journal of Economics, 118(3), 1007–1047.

    Article  Google Scholar 

  • Ballinger, T. P., & Wilcox, N. T. (1997). Decisions, error and heterogeneity. Economic Journal, 107(443), 1090–1105.

    Article  Google Scholar 

  • Becker, G. M., Degroot, M. H., & Marschak, J. (1964). Measuring utility by a single-response sequential method. Behavioral Science, 9(3), 226–232.

    Article  Google Scholar 

  • Berg, J. E., Dickhaut, J. W., & Rietz, T. A. (2010). Preference reversals: The impact of truth-revealing monetary incentives. Games and Economic Behavior, 68(2), 443–468.

    Article  Google Scholar 

  • Burks, S. V., Carpenter, J. P., Goette, L., & Rustichini, A. (2009). Cognitive skills explain economic preferences, strategic behavior, and job attachment. PNAS, 106(19), 7745–7750.

    Article  Google Scholar 

  • Camerer, C. F. (1989). An experimental test of several generalized utility theories. Journal of Risk and Uncertainty, 2(1), 61–104.

    Article  Google Scholar 

  • De Martino, B., Kumaran, D., Seymour, B., & Dolan Raymond, J. (2006). Frames, biases, and rational decision-making in the human brain. Science, 313(5787), 684–687.

    Article  Google Scholar 

  • Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19(4), 25–42.

    Article  Google Scholar 

  • Grether, D. M., & Plott, C. R. (1979). Economic theory of choice and the preference reversal phenomenon. American Economic Review, 69(2), 623–638.

    Google Scholar 

  • Hey, J., & Orme, C. (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica, 62(6), 1291–1326.

    Article  Google Scholar 

  • Levin, I. P., Schneider, S. L., & Gaeth, G. J. (1998). All frames are not created equal: A typology and critical analysis of framing effects. Organizational Behavior and Human Decision Processes, 76(2), 149–188.

    Article  Google Scholar 

  • Lichtenstein, S., & Slovic, P. (1971). Reversals of preference between bids and choices in gambling decisions. Journal of Experimental Psychology, 89(1), 46–55.

    Article  Google Scholar 

  • List, J. A. (2003). Does market experience eliminate market anomalies? The Quarterly Journal of Economics, 118(1), 41–71.

    Article  Google Scholar 

  • Loomes, G., Moffatt, P. G., & Sugden, R. (2002). A microeconometric test of alternative stochastic theories of risky choice. Journal of Risk and Uncertainty, 24(2), 103–130.

    Article  Google Scholar 

  • Schmidt, U., Starmer, C., & Sugden, R. (2008). Third-generation prospect theory. Journal of Risk and Uncertainty, 36(3), 203–223.

    Article  Google Scholar 

  • Seidl, C. (2002). Preference reversal. Journal of Economic Surveys, 16(5), 621–655.

    Article  Google Scholar 

  • Starmer, C., & Sugden, R. (1989). Probability and juxtaposition effects: An experimental investigation of the common ratio effect. Journal of Risk and Uncertainty, 2(2), 159–178.

    Article  Google Scholar 

  • Tversky, A., & Kahneman, D. (1981). The framing of decisions and the psychology of choice. Science, 211(4481), 453–458.

    Article  Google Scholar 

  • Zeiliger, R. (2000). A presentation of regate, internet based software for experimental economics. GATE, Lyon. http://www.gate.cnrs.fr/~zeiliger/regate/RegateIntro.ppt

Download references

Author information

Authors and Affiliations

  1. Département d’économie de l’école polytechnique, CNRS, 91128, Palaiseau Cedex, France

    Guillaume Hollard

  2. LED, Université Paris 8 (Saint-Denis), 2 Rue de la Liberté, 93200, Saint-Denis, France

    Hela Maafi

  3. Centre d’Économie de la Sorbonne, CNRS, 106/112 Boulevard de l’Hôpital, 75647, Paris Cedex 13, France

    Jean-Christophe Vergnaud

Authors
  1. Guillaume Hollard
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hela Maafi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jean-Christophe Vergnaud
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hela Maafi.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (docx 130 KB)

Appendices

Appendix 1: Correlation: supporting figures

See Figs. 8, 9 and 10.

Fig. 8
figure 8

\(\hbox {FE}_1\) vs instability (individual data)

Full size image
Fig. 9
figure 9

\(\hbox {FE}_1\) vs PR (individual data)

Full size image
Fig. 10
figure 10

Instability vs PR (individual data)

Full size image

Appendix 2: Framing effect: supporting figures

See Figs. 11, 12, 13 and 14.

Fig. 11
figure 11

Individual proportions of framing effects (round 3)

Full size image
Fig. 12
figure 12

Individual proportions of framing effects (rounds 1 and 3)

Full size image
Fig. 13
figure 13

Individual proportions of standard and non-standard framing effects (round 3)

Full size image
Fig. 14
figure 14

Individual proportions of standard and non-standard framing effects (rounds 1 and 3)

Full size image

Appendix 3: Framing effect: varying probability of winning and initial endowment

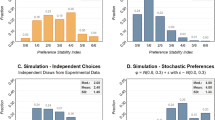
  • Figures 15, 16 and 17 show decisions across varying probabilities: the bars show the percentages (%) of trials in which subjects chose the gamble option in the gain frame (dark bar) and in the loss frame (lighter bar), for the four winning probabilities in the gamble option (20, 40, 60 and 80 %). Consistent with De Martino et al. (2006), we observe that subjects are more risk averse in the gain as compared to the loss frame for the four probabilities of winning.

Fig. 15
figure 15

The proportion gambling by winning probability (round 1)

Full size image
Fig. 16
figure 16

The proportion gambling by winning probability (round 3)

Full size image
Fig. 17
figure 17

The proportion gambling by winning probability (rounds 1 and 3)

Full size image

  • Figures 18, 19 and 20 show the decisions by the amount at stake: the bars show the percentages (%) of trials in which subjects chose the gamble option in the gain frame (dark bar) and in the loss frame(lighter bar), for the four amounts at stake in the gamble option (€10, €20, €30 and €40). As in De Martino et al. (2006), risk attitude is affected by the framing of questions for the different endowments, especially for high payoffs.

Fig. 18
figure 18

The proportion gambling by the initial endowment (round 1)

Full size image
Fig. 19
figure 19

The proportion gambling by the initial endowment (round 3)

Full size image
Fig. 20
figure 20

The proportion gambling by the initial endowment (rounds 1 and 3)

Full size image

Appendix 4: Framing effect: results in round 2

In round 2 (33 % of all the trials), the expected outcomes of the sure and the gamble option were unbalanced. We used these “catch trials” (1) to ensure that subjects remain engaged in the experiment (as in De Martino et al. 2006), and (2) to separate the two sets of questions where the sure and the gamble options had the same expected outcome. For both frames (gain and loss), we used two types of catch trials: the “gamble weighting” where the gamble option is preferable to the sure option, and the “sure weighting” where the sure option is preferable to the gamble option. We varied the attractiveness of the sure and gamble options in both frames (see Table 4) to examine the accuracy of optimal decisions according to the attractiveness of the options.

Figure 21 shows the proportion of gambling in the gain frame (dark bar) and in the loss frame (lighter bar). Subjects were accurate in making optimal choices, by generally gambling more (less) when the gamble option was more (less) favorable than the sure option. More precisely, we constructed an “attractiveness index” as the difference between the expected outcomes of the gamble and the sure option and found that the proportion of gambling is positively and significantly correlated with the attractiveness of the gamble option over the sure option (gain frame: rho \(=\) 0.2799, \({p}<0.01\). Loss frame: rho \(=\) 0.3324, \({p}<0.01\)).

Fig. 21
figure 21

The proportion gambling by the frame and the attractiveness of the sure and gamble options

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hollard, G., Maafi, H. & Vergnaud, JC. Consistent inconsistencies? Evidence from decision under risk. Theory Decis 80, 623–648 (2016). https://doi.org/10.1007/s11238-015-9518-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11238-015-9518-8

Keywords

JEL Classification

Search

Navigation