Performance analysis of end-to-end SNR estimators for AF relaying

Abstract

Many existing signal-to-noise ratio (SNR) estimators were designed and evaluated for conventional one-hop communications systems. However, for a relaying system, it is the end-to-end SNR that determines the system performance. In this paper, we will fill this gap by evaluating the performances of the existing SNR estimators in a dual-hop relaying system used for each hop. The probability density functions of the SNR estimators are first derived, whose parameters are fitted as functions of the sample size and the true value of SNR. Using them, the cumulative distribution functions of the end-to-end SNR and the bit error rate performance for a relaying system are derived. Numerical results show that the squared signal-to-noise variance estimator has the best performance for small SNRs and the second-order fourth-order moments estimator has the best performance for large SNRs, while the signal-to-variation ratio estimator has the worst performance, among the existing SNR estimators, for AF relaying systems.

1 Introduction

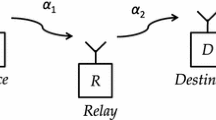
The idea of relaying is to forward signals from the source to the destination using one or more idle nodes via several hops. In contrast, the source in traditional systems sends signal to the destination directly via one hop. Among different relaying protocols, amplify-and-forward (AF) is a simple one, where the relay receives the signal from the source and then amplifies this signal and forwards it to the destination without any further processing. Thus, AF relays have short delays.

On the other hand, signal-to-noise ratio (SNR) estimation is a basic requirement in many communications systems. When the SNR is constant over a certain period of time, the knowledge of SNR can be used in various algorithms for optimal performance by SNR estimation. The knowledge of the SNR can be used to improve the performances of various systems. A lot of applications and techniques require the SNR knowledge for suitable operations. For instance, rate adaptation needs SNR information. Also, SNR knowledge is required in power control for code-division multiple-access systems, link adaptation for adaptive modulation and coding systems, and iterative decoding for “turbo” and low-density parity-check (LDPC) codes [1], in conventional system as well as in [2,3,4,5] for relaying systems where authors analysed the decode-and-forward (DF) and AF performances in two-way relaying or multi-way relay networks. Nonetheless, these works assumed perfect SNR knowledge and did not consider SNR estimation or SNR error.

Several SNR estimators have been proposed in the literature for traditional one hop systems. For example, the split symbol moments estimator (SSME) can provide an estimate of the symbol SNR for binary phase shift keying (BPSK) signals [6]. This estimator was designed for operation with additive white Gaussian noise (AWGN) and at low data rates so that the bandwidth limit is insignificant. Maximum-likelihood (ML) estimators were also derived from samples of a complex received signal using probability density functions in [7]. In addition to the SSME and ML estimators, another estimator called squared signal-to-noise variance (SNV) estimator was proposed in [8], where the SNV estimator using data decisions was first derived for BPSK modulation in real AWGN and then was extended to higher orders of modulation in complex channels. In [9], the second-order and fourth-order moments (M2M4) estimator was studied using the second- and fourth-order moments of the signal to avoid carrier phase recovery. In [10], signal-to-variation ratio (SVR) estimator was designed for M-ary PSK-modulated signals. An in-service SVR estimator for complex channels was also developed. All these estimators provide efficient estimation of SNR for different applications. However, their performances were only evaluated for the traditional one-hop systems in [11]. In order to improve performance for signal-to-noise ratio (SNR) estimator a new method has been proposed in [12]. For non-constant modulus constellations over flat-fading channel a new SNR estimation have been discussed in [13]. Signal-to-noise estimatation in time-varying fading channels have been considered in [14]. It is not clear how these estimators will perform in a relaying system that adopts two or more hops, as it is the end-to-end SNR that determines the performance of a relaying system. The exact end-to-end SNR describes the actual relaying performance but is complicated [15]. Several bounds have been proposed to simplify it. The harmonic mean has the mathematical tractability but is only a tight upper bound at high SNR [15]. The minimum hop SNR is a good indication of the asymptotic performance of the relaying system [15].

In this paper, we provide such a performance evaluation for SNR estimation in AF relaying systems by applying the estimators developed in [8,9,10,11] to each hop and examining the accuracy of the end-to-end SNR estimate in AF relaying. Different forms of the end-to-end SNR are considered: the exact end-to-end SNR, the harmonic mean and the minimum hop SNR. Also, the root mean squared error (RMSE) performances of the three expressions of the end-to-end SNR are first examined using simulation for each estimator above. Then, the probability density functions (PDFs) of the SNR estimates are derived, as they are not available in the literature. Based on these PDFs, the cumulative distribution functions (CDFs) of the three forms of the end-to-end SNR using these estimates are obtained in closed-form analytical expressions. The bit error rate is obtained using these CDFs. Numerical results show that the squared signal-to-noise variance (SNV) estimator has the best performance and the signal-to-variation ratio(SVR) estimator performs the worst for AF relaying system.

2 System model

2.1 AF relaying

This kind of relay serves as a repeater, where the relay receives the signals from the source and then amplifies the received signal and forwards it to the destination. AF relays are simple and have short delays. However, this kind of relays can amplify the noise in the signal too, shown in Fig. 1. Similar to [15,16,17,18], consider a cooperative diversity system with one relaying link between the source node and the destination node. In the first time slot, the amplified signal from the source is forwarded to the relay using an AF relaying protocol in flat fading channels with AWGN. In the second time slot, the signal from the relay is forwarded to the destination. The received signal at the relay can be given as:

$$\begin{aligned} u(t)=h_{1} \sqrt{E_0} x(t-T)+n_{1}(t) \end{aligned}$$

(1)

where $h_1$ is the fading gain of the source-to-relay link, $E_0$ is the transmitted signal power, $n_1 (t)$ is the Gaussian noise in the source-to-relay link with noise power $N_1$,x(t) is the transmitted signal. The received signal at the destination can be given as [15]

$$\begin{aligned} y(t)=h_{2}\alpha u(t)+n_{2}(t) \end{aligned}$$

(2)

where $h_2$ is the fading gain of the relay-to-destination link, $\alpha$ is the relay gain and $n_2 (t)$ is the Gaussian noise in the relay-to-destination link with noise power $N_2$.

Fig. 1

AF relaying model

2.2 SNR estimators

Consider a baseband equivalent, discrete and complex model of a coherent M-ary PSK signal in a complex AWGN channel. Assume perfect timing recovery. Assume that there are $N_{ss}=20$ samples for each symbol in a block of $N_{sym}$ symbols using a root raised-cosine (RRC) pulse-shaping filter with rolloff $=0.5$ and $L=127$, where L is the number of tap coefficients. The M-ary PSK symbols are then represented by [11]

$$\begin{aligned} a_n=e^{j\theta _n}, n={{0,1,\ldots ,N_{sym}-1}} \end{aligned}$$

(3)

where $\theta _n$ is the phase of the n-th symbol spaced evenly around the circle. The matched filter (MF) output is then given by [11]

$$\begin{aligned} y_n=y_{nN_{ss}}=\sqrt{S}a_n g_0 +\sqrt{N}w_{n} \end{aligned}$$

(4)

where $g_0$ is the peak of the full raised-cosine impulse response, S is a signal power scaling factor, N is the noise power scaling factor, $w_n$ is the symbol-spaced filtered noise samples represented by [11]

$$\begin{aligned} w_n=w_{nN_{ss}}={\sum _l^L} h_l z_{k-l} |_{k=nN_{ss}} \end{aligned}$$

(5)

$h_l$ is the RRC filter tap coefficients and $z_{k-l}$ is the complex, sampled, zero-mean AWGN of unit variance. Since $y_n$ represents the decision variable, the SNR can be expressed as [11]

$$\begin{aligned} \rho =\frac{E \left\{ |\sqrt{S}a_n g_0|^2\right\} }{var\left\{ \sqrt{N}w_n\right\} } \end{aligned}$$

(6)

where $E \{.\}$ and $VAR \{.\}$, respectively, represent the expectation and variance operations. The SNR is independent of the channel if the sum of the squares of the RRC tap coefficients is set to unity such that $g_0=1$ and $\rho =\frac{S}{N}$. Also, one can use data-aided (DA) estimators that depend on the information of the transmitted data. In the following, TxDA denotes the perfect knowledge of the transmitted symbol for a data-aided (DA) estimator, and RxDA denotes an estimator that uses estimates of the transmitted symbols or data decisions.

2.2.1 SNV estimator

The SNV RxDA estimator for BPSK was derived in [8] as

$$\begin{aligned} \begin{aligned}&\hat{\rho }_{SNV RxDA,complex}=\\&\frac{\left[ \frac{1}{N_{sym}}\sum _{n=0}^{N_{sym}-1}|y_n|\right] ^2}{\frac{1}{N_{sym}}\sum _{n=0}^{N_{sym}-1}|y_n|^2-\frac{1}{N_{sym} N_{sym}}\left[ \sum _{n=0}^{N_{sym}-1}|y_n|\right] ^2} \end{aligned}. \end{aligned}$$

(7)

When $N_{ss}=1$, the SNV estimator actually becomes the ML estimator [11]. While the ML estimator operates on one sample for each symbol at the output of the MF, the SNV estimator operates on multiple samples for each symbol at the output of the MF.

2.2.2 M2M4 estimator

Let $M_2$ represent the second-order moment of $y_n$ as [9]

$$\begin{aligned} \begin{aligned} M_2&=E\left\{ y_{n}y_{n}^{*}\right\} =S*E\left\{ |a_n|^2\right\} +\sqrt{SN}*E\left\{ a_{n}w_{n}^{*}\right\} \\&\quad +\sqrt{SN}*E\left\{ w_{n}a_{n}^{*}\right\} +N*E\left\{ |w_{n}|^2\right\} \end{aligned} \end{aligned}$$

(8)

and let $M_4$ represent the fourth-order moment of $y_n$ as [9]

$$\begin{aligned} M_4= & {} E\left\{ (y_{n}y_{n}^{*})^2\right\} \nonumber \\= & {} S^{2}E\left\{ |a_{n}|^{4}\right\} +2S\sqrt{SN}*\left( E\left\{ |a_{n}|^{2}a_{n}w_{n}^{*}\right\} \right. \nonumber \\&\left. +E\left\{ |a_{n}|^{2}w_{n}a_{n}^{*}\right\} +E\left\{ |a_{n}|^{2}w_{n} a_{n}^{*}\right\} \right) +SN\nonumber \\&\quad *\left( E\left\{ (a_{n}w_{n}^{*}\right) ^2\right\} +4E\left\{ |a_{n}|^{2}|w_{n}|^{2}\right\} +E\left\{ (a_{n}w_{n}^{*})^{2}\right\} \nonumber \\&+\,2N\sqrt{SN}*\left( E\left\{ |w_{n}|^{2}a_{n}w_{n}^{*}\right\} +E\left\{ |w_{n}|^{2}w_{n}a_{n}^{*}\right\} \right) \nonumber \\&+\,N^2E\left\{ |w_{n}|^{4}\right\} . \end{aligned}$$

(9)

For BPSK signals, the $M_{2}M_{4}$ estimator can be expressed as [11]

$$\begin{aligned} \hat{\rho }^{\prime }_{M_{2}M_{4},complex}=\frac{1}{2} \frac{\sqrt{6M_{2}^2- 2 M_4}}{M_{2}-\frac{1}{2} \sqrt{6M_{2}^2- 2 M_4}}. \end{aligned}$$

(10)

The $M_{2}M_{4}$ estimator is a type of in-service estimator which is based on the second- and fourth-order moments of the samples. The good point is that carrier phase recovery is not required in the $M_{2}M_{4}$ estimator because it is a moment-based estimator. It does not need to use the data decisions either.

2.2.3 SVR estimator

This estimator was designed to operate with any M-ary PSK-modulated signal. The SVR estimator for BPSK is [11]

$$\begin{aligned} \begin{aligned}&\hat{\rho }^{\prime }_{SVR,complex}=\\&\quad \frac{(\beta -1)\pm \sqrt{(\beta -1)^2-[1-\beta (k_{a}-1)][1-\beta (k_{w}-1)]}}{1-\beta ({k_{a}}-1)} \end{aligned}. \end{aligned}$$

(11)

where $k_{a}=E\left\{ |a_n|^4\right\} /E^2 \left\{ |a_n|^2\right\}$ is the kurtosis of the signal and $k_w=E\left\{ |w_n|^4\right\} /E^2 \left\{ |w_n|^2\right\}$ is the kurtosis of the noise.

2.3 End-to-end SNR expressions

2.3.1 Exact end-to-end SNR

The exact end-to-end SNR is derived in [15] as

$$\begin{aligned} \gamma _{eq_1}=\frac{\gamma _{1}\gamma _{2}}{\gamma _{1}+\gamma _{2}+1} \end{aligned}$$

(12)

where $\gamma _{1}=\frac{E_0|h_{1}|^2}{N_{1}}$ and $\gamma _{2}=\frac{E |h_{2}|^2}{N_{2}}$ are the instantaneous SNRs, E is the radiated energy at relay. The average SNRs are $\overline{\gamma }_1=\frac{E_0 \omega _1}{N_1}$ and $\overline{\gamma }_{2}=\frac{E \omega _{2}}{N_{2}}$ , where $\omega _{1}=E\left\{ |h_1|^2\right\}$ and $\omega _{2}=E\left\{ |h_2|^2\right\}$, $E\left\{ \cdot \right\}$ donotes the expectation operation. When $\gamma _{1}$ and $\gamma _{2}$ are estimated using the SNR estimators in Sect. II.A, one has

$$\begin{aligned} \hat{\gamma }_{eq_1}=\frac{\hat{\gamma }_{1} \hat{\gamma }_{2}}{\hat{\gamma }_{1}+ \hat{\gamma }_{2}+1} \end{aligned}$$

(13)

Table 1 MSE and RMSE of distribution fitting errors when SNR $=$ 20 dB

2.3.2 Hamonic mean

The major difficulty in (12) comes from the fact that $\gamma$ is a non-linear function of $\gamma _{1}$ and $\gamma _{2}$. The exact probability distribution function of $\gamma$ is not available. To overcome this difficulty, in the literature, one upper bound to the instantaneous SNR is widely used as the harmonic mean given by [18] as

$$\begin{aligned} \gamma _{eq_2} \approx \frac{\gamma _{1}\gamma _{2}}{\gamma _{1}+\gamma _{2}}. \end{aligned}$$

(14)

When $\gamma _{1}$ and $\gamma _{2}$ are estimated using the SNR estimators in Section II.A, one has

$$\begin{aligned} \hat{\gamma }_{eq_2} \approx \frac{\hat{\gamma }_{1} \hat{\gamma }_{2}}{\hat{\gamma }_{1}+\hat{\gamma }_{2}}. \end{aligned}$$

(15)

2.3.3 Minimum bound

Another approximation to $\gamma$ uses the minimum of $\gamma _{1}$ and $\gamma _{2}$ as

$$\begin{aligned} \gamma _{eq_3}\approx \frac{1}{2}min\left\{ \gamma _{1},\gamma _{2}\right\} . \end{aligned}$$

(16)

This bound is tight when $\gamma _{1}$ or $\gamma _{2}$ are large. When $\gamma _{1}$ and $\gamma _{2}$ are estimated using the SNR estimators in Section II.A, one has

$$\begin{aligned} \hat{\gamma }_{eq_3}\approx \frac{1}{2} min\left\{ \hat{\gamma }_{1},\hat{\gamma }_{2}\right\} . \end{aligned}$$

(17)

2.4 Gamma and Burr distributions

The distribution for the SNR estimators in (7), (10) and (11) are not available in the literature. However, we need them to analyze the relaying performance.Thus, we resort to the distribution fitting tool in MATLAB. We have tried all distributions provided by this tool. Table 1 compares several important distributions. Our tests show that the Gamma and Burr distributions give the most accurate fitting. Figure 2 compares the data with the fitting.The table show gamma distribution and burr distribution have the smallest fitting errors.

Fig. 2

Gamma and Burr distribution

This part gives the CDF expressions for the Gamma and Burr distributions, as they will be used later in the derivation and also in the approximation to the PDFs of the SNR estimators. The Gamma PDF is given by

$$\begin{aligned} f_{\hat{\gamma }_i}(\gamma )=\frac{1}{b_i^{a_i}\varGamma (a_i)} \gamma ^{a_i -1} exp\left( \frac{\gamma }{b_i}\right) \end{aligned}$$

(18)

where $a_i$ is the parameter describing the fading severity, $b_i$ is the average SNR, and $\varGamma (a_i)$ is the Gamma function. The Gamma CDF is given by:

$$\begin{aligned} F_{\hat{\gamma }_i}(\gamma )=1-\frac{\varGamma (a_i,\frac{\gamma }{b_i})}{\varGamma (a_i)} \end{aligned}$$

(19)

where $\varGamma (.,.)$ is the incomplete gamma function. The Burr PDF is given by

$$\begin{aligned} f_{\hat{\gamma }_i}(\gamma )=c_{i}k_{i} \frac{\gamma ^{c_{i}-1}}{(1+\gamma ^{c_i})^{k_i+1}} \end{aligned}$$

(20)

where $c_i$ and $k_i$ are the parameters of the Burr distribution. The Burr CDF is given by

$$\begin{aligned} F_{\hat{\gamma }_i}(\gamma )=1-(1+\gamma ^{c_i})^{- k_i}. \end{aligned}$$

(21)

3 Derivation of CDF

This section derives the CDFs for different forms of end-to-end SNR using the Gamma and Burr approximations to the SNR estimators.

3.1 Exact end-to-end SNR

3.1.1 Gamma approximation

The exact cumulative distribution function $F_{\hat{\gamma }_{eq_1}}(\gamma )$ for (13) using the Gamma approximations of $\hat{\gamma }_{1}$ and $\hat{\gamma }_{2}$ can be expressed as

$$\begin{aligned} \begin{aligned} F_{\gamma _{\hat{\gamma }_{eq_1}}}(\gamma )&=Pr\left[ \frac{\hat{\gamma }_{1}\hat{\gamma }_2}{\hat{\gamma }_{1}+\hat{\gamma }_{2}+1}\le \gamma \right] \\&=Pr\left[ \hat{\gamma }_{1}\ge \frac{\gamma (\hat{\gamma }_{2}+1)}{\hat{\gamma }_{2}-\gamma }|\hat{\gamma }_2<\gamma \right] \\&\quad +Pr\left[ \hat{\gamma }_1\le \frac{\gamma (\hat{\gamma }_{2}+1)}{\hat{\gamma }_{2}-\gamma }|\hat{\gamma }_2>\gamma \right] \\&=I_1+I_2 \end{aligned} \end{aligned}$$

(22)

where $\hat{\gamma }_{1}$ and $\hat{\gamma }_{2}$ are approximated by the Gamma distribution and

$$\begin{aligned} \begin{aligned} I_{1}&=Pr\left\{ \hat{\gamma }_{2}<\gamma \right\} =\int _{0}^{\gamma } {f_{\hat{\gamma }_2}(y)}dy\\&=F_{\hat{\gamma }_2}(y)\\&=1-\frac{\varGamma \left( a_{2},\frac{\gamma }{b_2}\right) }{\gamma _{a_2}} \end{aligned} \end{aligned}$$

(23)

$$\begin{aligned} I_2= & {} \int _{\gamma }^{\infty } F_{\hat{\gamma }_1}\left( \frac{\gamma (y+1)}{y-\gamma }\right) f_{\hat{\gamma }_2}(y)dy\nonumber \\= & {} \int _{\gamma }^{\infty } \left\{ 1-\frac{\varGamma \left( a_1,\frac{1}{b_1} \gamma \left( \frac{y+1}{y-\gamma }\right) \right) }{\varGamma (a_1)} \right\} f_{\hat{\gamma }_2}(y)dy\nonumber \\= & {} \int _{\gamma }^{\infty } f_{\hat{\gamma }_2}(y)dy-\int _{\gamma }^{\infty } \frac{\varGamma \left( a_1,\frac{1}{b_1}\gamma \left( \frac{y+1}{y-\gamma }\right) \right) }{\varGamma (a_1)} f_{\hat{\gamma }_2}(y)dy\nonumber \\= & {} \int _{\gamma }^{\infty } \frac{1}{b_2^{a_2}\varGamma (a_2)} y^{a_{2}-1}exp\left( -\frac{y}{b_2}\right) dy\nonumber \\&\quad -\int _{\gamma }^{\infty } \frac{\varGamma \left( a_1,\frac{1}{b_1}\gamma \left( \frac{y+1}{y-\gamma }\right) \right) }{\varGamma (a_1)}\nonumber \\&\quad *\frac{1}{b_2^{a_2}\varGamma (a_2)} y^{a_{2}-1} exp\left( -\frac{y}{b_2}\right) dy\nonumber \\= & {} \frac{\varGamma \left( a_2,\frac{\gamma }{b_2}\right) }{\varGamma (a_2)}-\frac{1}{b_2^{a_2}\varGamma (a_1)\varGamma (a_2)}I_3 \end{aligned}$$

(24)

with

$$\begin{aligned} I_3=\int _{\gamma }^{\infty } y^{a_{2}-1}exp\left( -\frac{y}{b_2}\right) \times \varGamma \left( a_{1},\frac{\gamma }{b_1}\left( \frac{y+1}{y-\gamma }\right) \right) dy . \end{aligned}$$

(25)

The integral $I_3$ can be written in the general form as

$$\begin{aligned} I_3=\int _{\gamma }^{\infty } x^{a-1} exp(-bx)\times \varGamma \left( c,d\left( \frac{x+e}{x-\gamma }\right) \right) dx \end{aligned}$$

(26)

where a, b, c, d, e are constants and [19]

$$\begin{aligned} \begin{aligned} \varGamma \left( c,d\left( \frac{x+e}{x-\gamma }\right) \right) dx&=(c-1)!e^{(-d)}\times e^{\left[ -d\left( \frac{x+e}{x-\gamma }\right) \right] }\\&*\sum _{k=0}^{c-1}\sum _{l=0}^k \frac{d^k}{k!}. \begin{pmatrix}k\\ l \end{pmatrix} \left( \frac{x+e}{x-\gamma }\right) ^l . \end{aligned} \end{aligned}$$

(27)

Thus, one has

$$\begin{aligned}&\begin{aligned} I_3&=(c-1)! exp(-(d+b\gamma ))\\&*\sum _{k=0}^{c-1}\sum _{l=0}^k \sum _{r=0}^{a-1} \frac{d^k}{k!} \begin{pmatrix} k\\ l \end{pmatrix} \begin{pmatrix} a-1\\ r \end{pmatrix}(\gamma +e)^l \gamma ^{a-r-1} \\&\times \int _{0}^{\infty } x^{r-l}exp(-bx) exp\left[ -d\left( \frac{\gamma +e}{x}\right) \right] dx \end{aligned} \end{aligned}$$

(28)

$$\begin{aligned}&\begin{aligned}&\int _{0}^{\infty } x^{r-1} exp(-bx)exp\left[ -d\left( \frac{\gamma +e}{x}\right) \right] dx=\\&2\sum _{k=0}^{c-1}\sum _{l=0}^k\sum _{r=0}^{a-1}(\gamma +e)^{\frac{r+1}{2}} \left( \frac{d}{b}\right) ^{\frac{r-l+1}{2}} K_{l-r-1} 2\sqrt{bd(\gamma +e)} \end{aligned} \end{aligned}$$

(29)

Finally,

$$\begin{aligned} I_3= & {} 2(a_1-1)! exp\left[ -\left( \frac{\gamma }{b_1}+\frac{\gamma }{b_2}\right) \right] \nonumber \\&\times \sum _{k=0}^{a_{1}-1} \sum _{l=0}^{k} \sum _{r=0}^{a_2-1} \left( \frac{1}{k!}\right) \times \begin{pmatrix} k\\ l \end{pmatrix} \times \begin{pmatrix} a_2-1\\ r \end{pmatrix} \times \left( \frac{1}{b_2}\right) ^{\frac{l-r-2}{2}} \nonumber \\&\times \left( \frac{1}{b_1}\right) ^{\frac{2k-l+r+1}{2}}\times \gamma ^{\frac{2k+2a_2-l-r-1}{2}}\times (\gamma +1)^{\frac{l+r+1}{2}} \nonumber \\&\times K_{l-r-1} \left( 2\sqrt{\frac{\gamma (1+\gamma )}{b_1b_2}}\right) \end{aligned}$$

(30)

The integral $I_3$ in (30) is solved in closed-form expression. Using (30) and after some straightforward mathematical manipulations, $F_{\gamma _{eq_1}}(\gamma )$ can be derived as

$$\begin{aligned} F_{\gamma _{eq_1}}(\gamma )= & {} 1-\frac{2(a_{1}-1)!exp\left[ -\left( \frac{\gamma }{b_{1}} + \frac{\gamma }{b_{2}}\right) \right] }{b_{2}^{a_2}\varGamma (a_1)\varGamma (a_2)}\nonumber \\&\times \sum _{k=0}^{a_{1}-1} \sum _{l=0}^{k} \sum _{r=0}^{a_{2}-1} \left( \frac{1}{k!}\right) \begin{pmatrix} k\\ l \end{pmatrix} \times \begin{pmatrix} a_{2}-1\\ r \end{pmatrix} \left( \frac{1}{b_2}\right) ^{\frac{l-r-1}{2}}\nonumber \\&\times \left( \frac{1}{b_1}\right) ^{\frac{2k-l+r+1}{2}}\times \gamma ^{\frac{2k+2a_{2}-l-r-1}{2}}(\gamma +1)^{\frac{l+r+1}{2}} \nonumber \\&\times K_{l-r-1} \left( 2\sqrt{\frac{\gamma (1+\gamma )}{b_{1}b_{2}}}\right) \end{aligned}$$

(31)

where $a_{1}$, $a_{2}$, $b_{1}$ and $b_{2}$ are the parameters of the Gamma distributions for $\hat{\gamma }_1$ and $\hat{\gamma }_2$ to be determined later.

3.1.2 Burr approximation

The Burr distribution is found to give good approximations to the PDFs of the SNR estimates too. The Burr CDF $F_{\gamma _{eq_1}}(\gamma )$ for the exact end-to-end SNR can be expressed as

$$\begin{aligned} \begin{aligned} F_{\gamma _{\hat{\gamma }_{eq_1}}}(\gamma )&=Pr\left[ \frac{\hat{\gamma }_{1}\hat{\gamma }_2}{\hat{\gamma }_{1}+\hat{\gamma }_{2}+1}\le \gamma \right] \\&=Pr\left[ \hat{\gamma }_{1}\ge \frac{\gamma (\hat{\gamma }_{2}+1)}{\hat{\gamma }_{2}-\gamma }|\hat{\gamma }_2<\gamma \right] \\&\quad +Pr\left[ \hat{\gamma }_1\le \frac{\gamma (\hat{\gamma }_{2}+1)}{\hat{\gamma }_{2}-\gamma }|\hat{\gamma }_2>\gamma \right] \\&=I_1+I_2 \end{aligned} \end{aligned}$$

(32)

where $\hat{\gamma }_{1}$ and $\hat{\gamma }_{2}$ are approximated by the Burr distributions and

$$\begin{aligned} I_{1}= & {} \int _{\gamma }^{0} f_{\gamma _2}(y)dy=F_{\gamma _2}(y)=1-(1+y_{c_2})^{-k_2}\end{aligned}$$

(33)

$$\begin{aligned} I_2= & {} \int _{\gamma }^{\infty } F_{\hat{\gamma }_1}\left[ \frac{\gamma (y+1)}{y-\gamma }\right] f_{\hat{\gamma }_2}(y)dy\nonumber \\= & {} \int _{\gamma }^{\infty } \left\{ 1-\left[ 1+\left( 1+\left( \frac{\gamma (y+1)}{y-\gamma }\right) ^{c_1}\right) ^{-k_1}\right] \right\} * c_{2}*k_{2}\nonumber \\&* \frac{y^{c_{2}-1}}{(1+y^{c_2})^{k_{2}+1}}dy\nonumber \\= & {} (1+y^{c_2})^{-k_2}-I_3 \end{aligned}$$

(34)

$$\begin{aligned} \begin{aligned} I_3&=\int _{\gamma }^{\infty } \frac{[(y-\gamma )^{c_1}+\gamma ^{c_1}(y+1)^{c_1}]^{-k_{1}}}{(y-\gamma )^{-c_{1}k_{1}}}\\&\quad \times c_{2}k_{2} \frac{y^{c_{2}-1}}{(1+y^{c_2})^{k_{2}+1}}dy \end{aligned} \end{aligned}$$

(35)

Thus,

$$\begin{aligned} \begin{aligned} F_{\gamma _{eq_1}}(\gamma )&=1-\int _{\gamma }^{\infty } \frac{[(y-\gamma )^{c_1}+\gamma ^{c_1}(y+1)^{c_1}]^{-k_1}}{(y-\gamma )^{-c_{1} k_1}}\\&\quad \times c_{2} k_{2} \frac{y^{c_{2}-1}}{(1+y^{c_2})^{k_2+1}}dy \end{aligned} \end{aligned}$$

(36)

where $c_{1}$,$c_{2}$, $k_{1}$ and $k_{2}$ are parameters of the Burr distribution. The integration can’t be solved due to its complexity.

3.2 Harmonic mean

3.2.1 Gamma approximation

Repeating the steps above, we can get the Gamma approximation for the harmonic mean $F_{\hat{\gamma }_{eq_2}(\gamma )}$ as

$$\begin{aligned} \begin{aligned} F_{\hat{\gamma }_{eq_2}}(\gamma )&=Pr\left[ \frac{\hat{\gamma }_{1}\gamma _{2}}{\hat{\gamma }_{1}+\hat{\gamma }_{2}}\le \gamma \right] \\&=Pr\left[ \hat{\gamma }_{1}\ge \frac{\gamma \hat{\gamma }_{2}}{\hat{\gamma }_{2}-\gamma }|\hat{\gamma }_{2}<\gamma \right] \\&\quad +Pr\left[ \hat{\gamma }_{1}\le \frac{\gamma \hat{\gamma }_{2}}{\hat{\gamma }_{2}-\gamma }|\hat{\gamma }_{2}>\gamma \right] \\ \end{aligned} \end{aligned}$$

(37)

which can be solved as

$$\begin{aligned} F_{\hat{\gamma }_{eq_2}}(\gamma )&=1-\frac{2(a_{1}-1)!exp[-(b_{1} \gamma + b_{2} \gamma )]}{b_{2}^{a_2}\varGamma (a_1)\varGamma (a_2)}\nonumber \\&\quad \times \sum _{k=0}^{a_{1}-1} \sum _{l=0}^k \sum _{r=0}^{a_{2}-1}\frac{1}{k!} \begin{pmatrix} k\\ l \end{pmatrix} \times \begin{pmatrix} a_2-1\\ r \end{pmatrix} \left( \frac{1}{b_2}\right) ^{\frac{l-r-1}{2}}\nonumber \\&\quad \times \left( \frac{1}{b_1}\right) ^{\frac{2k-l+r+1}{2}} \times \gamma ^{\frac{2k+2 a_{2}-l-r-1}{2}} (\gamma +1)^{\frac{l+r+1}{2}}\nonumber \\&\quad \times K_{l-r-1} \left( 2\sqrt{\frac{\gamma ^2}{b_{1}b_{2}}}\right) . \end{aligned}$$

(38)

3.2.2 Burr approximation

The harmonic mean using the Burr approximation can give $F_{\hat{\gamma }_{eq_2}}(\gamma )$ as

$$\begin{aligned} \begin{aligned} F_{\gamma _{\hat{\gamma }_{eq_1}}}(\gamma )&=Pr\left[ \frac{\hat{\gamma }_{1}\hat{\gamma }_2}{\hat{\gamma }_{1}+\hat{\gamma }_{2}+1}\le \gamma \right] \\&=I_1+I_2 \end{aligned} \end{aligned}$$

(39)

which is solved to give

$$\begin{aligned} \begin{aligned} F_{\hat{\gamma }_{eq_2}}(\gamma )&=1-\int _{\gamma }^{\infty } \frac{[(y-\gamma )^{c_1}+\gamma y^{c_1}]^{-k_1}}{(y-\gamma )^{-c_{1} k_1}}\\&\quad \times c_{2} k_{2} \frac{y^{c_{2}-1}}{(1+y^{c_2})^{k_2+1}}dy. \end{aligned} \end{aligned}$$

(40)

3.3 Minimum bound

3.3.1 Gamma approximation

The minimum bound has the cumulative distribution function $F_{\hat{\gamma }_{eq_3}}(\gamma )$ as

$$\begin{aligned} F_{\hat{\gamma }_{eq_3}}(\gamma )=1-(1-F_{\hat{\gamma }_1}(\gamma ))(1-F_{\hat{\gamma }_2}(\gamma )). \end{aligned}$$

(41)

Using the Gamma approximation, $F_{\hat{\gamma }_{eq_3}}(\gamma )$ can be solved as

$$\begin{aligned} \begin{aligned} F_{\hat{\gamma }_{eq_3}}(\gamma )&=1-(1-F_{\hat{\gamma }_1}(\gamma ))(1-F_{\hat{\gamma }_2}(\gamma ))\\&=1-\left( 1-1-\frac{\varGamma \left( a_1,\frac{\gamma }{b_1}\right) }{\varGamma (a_1)}\right) \\&\quad *\left( 1-1-\frac{\varGamma \left( a_{2},\frac{\gamma }{b_2}\right) }{\varGamma (a_2)}\right) \\&=1-\left( \frac{\gamma (a_1,{\gamma }{b_1})}{\varGamma (a_1)}\right) \left( \frac{\varGamma (a_2,{\gamma }{b_2})}{\varGamma (a_2)}\right) . \end{aligned} \end{aligned}$$

(42)

3.3.2 Burr approximation

The minimum bound using the Burr approximation gives $F_{\hat{\gamma }_{eq_1}}(\gamma )$ is given by

$$\begin{aligned} \begin{aligned} F_{\hat{\gamma }{eq_3}}(\gamma )&=1-(1-F_{\hat{\gamma }_1}(\gamma ))(1-F_{\hat{\gamma }_2}(\gamma ))\\&=1-(1-1-(1+\gamma ^{c_1})^{-k_1})\\&\quad *(1-1-(1+\gamma ^{c_2})^{-k_2})\\&=1-(1+\gamma ^{c_2})^{-k_2} (1+\gamma ^{c_2})^{-k_2}. \end{aligned} \end{aligned}$$

(43)

Table 2 $a_i$ using the SNV estimator

3.4 BER for exact bound using Gamma and Burr distributions

In addition, we analyse the average bit error rate(BER) for Gamma and Burr distributions used in the exact SNR. The functions have been derived below.

$$\begin{aligned}&\begin{aligned}&BER=\int _{0}^{\infty }\left( \frac{1}{2}erfc\left( \sqrt{\gamma }\right) \right) f_{\gamma _{eq1}}(\gamma )d\gamma \\&\quad =\int _{0}^{\infty }\left( \frac{1}{2}erfc\left( \sqrt{\gamma }\right) \right) dF_{\gamma _{eq1}}(\gamma )\\&\quad ={\left[ \left( \frac{1}{2}erfc(\sqrt{\gamma })\right) F_{\gamma _{eq1}}(\gamma )\right] }_0^{\infty }\\&\qquad -\int _{0}^{\infty }\frac{1}{2}\frac{derfc\left( \sqrt{\gamma }\right) }{d\gamma }F_{\gamma _{eq1}}d\gamma \\ \end{aligned} \end{aligned}$$

(44)

$$\begin{aligned}&\quad \begin{aligned}&\frac{1}{2}\frac{derfc\left( \sqrt{\gamma }\right) }{d\gamma }=-\frac{e^{-\gamma }}{2\sqrt{\pi \gamma }} \end{aligned} \end{aligned}$$

(45)

Thus, the BER function for Gamma distribution can be expressed as

$$\begin{aligned}&BER_{gamma}=0+\frac{1}{2}\int _{0}^{\infty } \frac{e^{-\gamma }}{\sqrt{\pi \gamma }}\nonumber \\&\quad \left( 1-\frac{2(a_{1}-1)!exp\left[ -\left( \frac{\gamma }{b_{1}} + \frac{\gamma }{b_{2}} \right) \right] }{b_{2}^{a_2}\varGamma (a_1)\varGamma (a_2)}\right. \nonumber \\&\quad \times \sum _{k=0}^{a_{1}-1} \sum _{l=0}^{k} \sum _{r=0}^{a_{2}-1} \left( \frac{1}{k!}\right) \begin{pmatrix} k\\ l \end{pmatrix} \times \begin{pmatrix} a_{2}-1\\ r \end{pmatrix} \left( \frac{1}{b_2}\right) ^{\frac{l-r-1}{2}}\nonumber \\&\quad \times \left( \frac{1}{b_1}\right) ^{\frac{2k-l+r+1}{2}}\times \gamma ^{\frac{2k+2a_{2}-l-r-1}{2}}(\gamma +1)^{\frac{l+r+1}{2}} \nonumber \\&\left. \quad \times K_{l-r-1} \left( 2\sqrt{\frac{\gamma (1+\gamma )}{b_{1}b_{2}}}\right) \right) d\gamma \end{aligned}$$

(46)

And the BER function for Burr distribution can be expressed as

$$\begin{aligned}&BER_{burr}=0\nonumber \\&\quad +\frac{1}{2}\int _{0}^{\infty } \frac{e^{-\gamma }}{\sqrt{\pi \gamma }}\left( 1-\int _{\gamma }^{\infty } \frac{[(y-\gamma )^{c_1}+\gamma ^{c_1}(y+1)^{c_1}]^{-k_1}}{(y-\gamma )^{-c_{1} k_1}}\right. \nonumber \\&\qquad \left. \times c_{2} k_{2} \frac{y^{c_{2}-1}}{(1+y^{c_2})^{k_2+1}}\right) dyd\gamma \nonumber \\&\quad =\frac{1}{2}-\frac{1}{2}\int _{0}^{\infty }\int _{\gamma }^{\infty } \frac{e^{-\gamma }}{\sqrt{\pi \gamma }} \frac{[(y-\gamma )^{c_1}{+}\gamma ^{c_1}(y+1)^{c_1}]^{-k_1}}{(y-\gamma )^{-c_{1} k_1}}\nonumber \\&\qquad \times c_{2} k_{2} \frac{y^{c_{2}-1}}{(1+y^{c_2})^{k_2+1}}dyd\gamma \end{aligned}$$

(47)

Results for harmonic mean and the minimum hop SNR bound can be derived similarly. They are not presented here.

4 Sample PDFs of SNR estimates and their fitting

In this section, we generate samples of the SNR estimates $\hat{\gamma }_i$ for different values of ${\gamma }_i$ and different values of sample size. Then, we use the distribution fitting tool in MATLAB to fit the samples of the SNR estimates $\hat{\gamma }_i$ to different distributions. After trying different distributions, we have found that the Gamma and Burr distributions fit the PDFs of $\hat{\gamma _i}$ the best,as mentioned before. The specific steps are described as follows:

Step 1 The value of ${\gamma }_i$ is set from 1 to 40 dB with an interval of 2 dB. Thus, we have 19 different values of ${\gamma }_i$. The value of the sample size K is set from 100 to 1000 with an interval of 100. Thus, we have 10 different values of K.

Step 2 For each value of ${\gamma }_i$ and each value of K, we generate K samples in (2) with $\rho = {\gamma }_i$. We use the K samples in the SNV, M2M4 and SVR estimators to obtain three different estimators of ${\gamma }_i$.

Step 3 We repeat Step 2 for 10,000 times. Thus, we will have 10,000 estimates of ${\gamma }_i$ for the SNV estimator, 10,000 estimates of ${\gamma }_i$ for the M2M4 estimator and 10,000 estimates of ${\gamma }_i$ for the SVR estimator.

Step 4 Using the 10,000 estimates of ${\gamma }_i$, we perform distribution fitting in MATLAB using the Gamma and Burr distributions. The fitting will give us a pair of $a_i$ and $b_i$ for Gamma and a pair of $c_i$ and $k_i$ for Burr for each estimator.

Step 5 We repeat Step 2, Step 3 and Step 4 for different values of ${\gamma }_i$ and K. Each gives us a pair of a pair of $a_i$ and $b_i$ and $c_i$ and $k_i$ for each estimator.

Following these steps, we have a $19\times 10$ matrix for $a_i$, $b_i$, $c_i$ and $k_i$ for different estimators. Table 2 gives the fitted values of $a_i$ for different values of ${\gamma }_i$ and K using the SNV estimator. Other matrices for other parameters and other estimators are also available but are not given here to save space.

Table 3 Gamma and Burr distribution parameter functions

Using the values of $a_i$, $b_i$, $c_i$ and $k_i$ from distribution fitting for different values of ${\gamma }_i$ and K and different estimators, we can then use curve fitting to find $a_i$, $b_i$, $c_i$ and $k_i$ as functions of ${\gamma }_i$ and K Table 3 gives the curve-fitting results. Using Table 3 and Eqs. (18)–(21), the PDFs of the estimates $\hat{\gamma _1}$ and $\hat{\gamma _2}$ are obtained and used in Sect. 4 for derivation.

Fig. 3

Estimator root mean squared error for the a exact bound b harmonic mean bound c minimum hop SNR bound using 100 samples

5 Numerical results and discussion

This section compares the performances of the three estimators (second- and fourth-order moments estimator, signal-to-variation ratio estimator and squared signal-to-noise variance estimator) used in the AF relaying for the end-to-end SNR. We use computer simulation to find the mean squared error (MSE) values for each estimator. Then, the square root of the MSE is calculated to obtain the estimator root mean squared error (RMSE) in dB.

5.1 Different estimator performances

Figure 3 shows the root mean squared errors by using 100 samples for the exact end-to-end SNR, the harmonic mean and the minimum hop SNR bound. One sees that for small SNRs, the SNV estimator has higher RMSE than the SVR estimator and the M2M4 estimator. Then, all of them decrease when the SNR increases. The M2M4 estimator and the SNV estimator have similar RMSE values when the true value of SNR is larger than 10 dB, but the SVR estimator’s RMSE increases when the SNR is larger than 15 dB.

Comparing the accuracies of the bounds, we can see from Fig. 3 that the estimators have the largest RMSE for the exact end-to-end SNR and the harmonic mean and the smallest RMSE for the minimum hop SNR bound. This is because the minimum hop SNR bound is only affected by the estimation error of either $\hat{\gamma }_1$ or $\hat{\gamma }_2$, while the exact ann harmonic mean are affected by both.

Fig. 4

Estimator root mean squared error for the a exact bound b harmonic mean bound c minimum hop SNR bound using 1000 samples

Figure 4 shows three estimators’ root mean squared errors by using 1000 samples. Similar observations can be made. Again, the SNV estimator and the M2M4 estimator have decreasing RMSE when the SNR increases, and the SVR estimator has RMSE first decrease then increase when the SNR increases.

Fig. 5

Estimator bias for the exact end-to-end SNR using a 100 samples b 1000 samples

Figure 5 shows the estimator bias by using 100 and 1000 samples for the exact end-to-end SNR. The SNV estimator has a decreasing bias when the SNR increases, and the SVR estimator has a bias first increasing then decreasing when the SNR increases. Three estimators have similar bias values when the SNR is larger than 5 dB.

Comparing the performances of the SNV, M2M4 and SVR estimators using the figures, we conclude that the SVR estimator performance is worse than the other two estimators, while the SNV estimator has the best performance for large SNRs and the M2M4 estimator has the best performance for small SNRs. All estimator performances are improving when increasing the sample size. However, the M2M4 estimator and SVR estimator have similar performances in most cases.

Fig. 6

The cumulative distribution function of the a exact end-to-end SNR b hamonic mean end-to-end SNR c minimum end-to-end SNR for SNR $=$ 11 dB using the Burr distribution

5.2 Comparing the CDFs of end-to-end SNR estimate

Figure 6 shows the CDFs by using the Burr distribution for the exact, the harmonic mean, the minimum hop SNR bound with a fixed SNR 11 dB. We can see that the SNV and M2M4 estimators have overlapping CDFs in all cases, all of which approach 1 when $\gamma$ increases.

By comparing the CDF figures of different bounds, we can see the exact end-to-end SNR has the best performance since the three estimators approach 1 faster than the other two bounds.

Fig. 7

Bit-error-rate (BER) for the a Gamma distribution b Burr distribution

5.3 Bit-error-rate for Gamma and Burr distribution

Figure 7 shows the the bit error rate using the Gamma and Burr approximations when K $=$ 100 for different values of SNR. Both gamma distribution and burr distribution have decreasing bit-error-rate when the SNR increases as expected. Also, their bit error rate performances are almost identical, indicating that both approximations have similar accuracies.

Similar observations can be made for gamma distribution and burr distribution. Comparing the performance of gamma distribution and burr distribution, we conclude that they have similar performances in most cases.

6 Conclusion

This paper has used the distribution fitting toolbox and curve fitting toolbox in MATLAB to approximate the SNR estimates of SNV, M2M4 and SVR using the Gamma distribution and the Burr distribution.

The estimator root mean squared error has been simulated and simulation shows that the SNV estimator has the best performance for small SNRs and the M2M4 estimator has the best performance for large SNRs, while SVR has the worst performance.

Also, the CDF for each distribution for different expressions of the end-to-end SNR have been derived.