What is an experiment in mathematical practice? New evidence from mining the Mathematical Reviews

Abstract

From a purely formalist viewpoint on the philosophy of mathematics, experiments cannot (and should not) play a role in warranting mathematical statements but must be confined to heuristics. Yet, due to the incorporation of new mathematical methods such as computer-assisted experimentation in mathematical practice, experiments are now conducted and used in a much broader range of epistemic practices such as concept formation, validation, and communication. In this article, we combine corpus studies and qualitative analyses to assess and categorize the epistemic roles experiments are seen—by mathematicians—to have in actual mathematical practice. We do so by text-mining a corpus of reviews from the Mathematical Reviews, which include the indicator word “experiment”. Our qualitative, grounded classification of samples from this corpus allows us to explore the various roles played by experiments. We thus identify instances where experiments function as references to established knowledge, as tools for heuristics or exploration, as epistemic warrants, as communication or pedagogy, and instances simply proposing experiments. Focusing on the role of experiments as epistemic warrants, we show through additional sampling that in some fields of mathematics, experiments can warrant theorems as well as methods. We also show that the expressed lack of experiments by reviewers suggests concordant views that experiments could have provided epistemic warrants. Thus, our combination of corpus studies and qualitative analyses has added a typology of roles of experiments in mathematical practice and shown that experiments can and do play roles as epistemic warrants depending on the mathematical field.

1 Introduction

During the 1990s, the role of computer-assisted experimentation in mathematics attracted new attention to non-deductive and heuristic practices. Access to desktop hardware and general-purpose software allowed mathematicians to use experiments for a variety of purposes spanning visualization, numerical exploration, formula manipulation, and proof construction (see Borwein & Bailey, 2004). In 1992, the Journal of Experimental Mathematics was founded, and around it and some seminal mathematicians such as Jonathan Borwein (1951–2016) and David H. Bailey, an experimental culture that often transcended mathematical fields began to form (Sørensen, 2016).

The new “experimental” approach to mathematics caused polemic disagreements, not least when it came to the epistemic role of experiments (Sørensen, 2010). Traditionally, experiments were thought to be confined to the realms of heuristics and pedagogy, but proponents argued for a more nuanced view of the role of (computer) experiments in verification and concept formation. In turn, these new interests in non-deductive aspects of mathematics attracted the attention of philosophers of mathematics with an interest in the discussions about mathematical practice (Baker, 2008; Van Bendegem, 1998). Among the first conclusions to be reached was that experiments were not new to mathematics, and neither were they exclusively tied to the use of computers (see e.g. Van Bendegem, 1998). A slightly different track of discussions centered on the use of computers in so-called computer assisted proofs and whether this practice made mathematics an a posteriori science. These discussions however have since split from the discussion of experiments per se, and we will not track them further in this paper (Burge, 1998; Johansen & Misfeldt, 2016; McEvoy, 2013; Tymoczko, 1979).

Since the late 1990s, Borwein and his collaborators have been able to argue the relevance of experimental mathematics by sheer success: They published extensively using their methods, they were able to use experimental mathematics to teach mathematics, and they argued for the philosophical relevance of computers and experiments in a number of contexts.

However, most of the successes of experimental mathematics which were studied by philosophers of mathematical practice fall within a relatively small scope of mathematical fields, and indeed, most philosophical studies have been focused on successes where experiments have challenged or supplemented existing methods.

Another strand in the philosophy of mathematical practice has focused on how experts and learners come to establish conviction about and trust in mathematical results (Andersen, 2020; Andersen et al., 2021; Weber et al., 2014). Using a variety of methods, such research has shown that experiments, examples, authority and other non-deductive forms of knowledge play much larger roles in establishing conviction than a purely formalist, autonomous (individual-centred) epistemology would accept.

Yet, as is still often the case in the philosophy of mathematical practice, philosophical analyses have predominantly been based on exemplars of interesting practices with only few methods to include the (potential) diversity of said practices (Löwe & Kerkhove, 2019). One step in the direction of more broadly empirically based and grounded analyses of larger and more complex practices is currently being taken with the first efforts to develop digital methods of large-corpus studies of mathematical practice. In this paper, we continue in that paradigm, asking “from large written corpora, what constitute experiments and, in particular, what roles do they play in mathematics as it is practiced?”.

1.1 MR as a source for mathematical practice

Among the digitally available corpora that allow access to mathematical practice, the post-publication peer reviews collected in Mathematical Reviews (MR) offer a mine yet to be explored. Compiled since the 1940s, these MR have provided mathematicians with an overview of their field; and their records have been made searchable and put online under the auspices of the American Mathematical Society (AMS). These reviews of published papers and books are written by peers in the community of intended readers, and the reviews combine factual information about the contents of the publication with short evaluations and criticisms from the reviewers. Obviously, these reviews are also heavily encoded in a particular genre, but the MR offers a glimpse into the practices by which the mathematical community takes in new results and evaluate them.

For this article, we combined big-data corpus studies with qualitative grounded analyses to provide a new perspective on the roles of experiments in contemporary research practices in the mathematical disciplines.

We mined the Mathematical Reviews for entries related to experiments, and through an iterative process of qualitative and quantitative analyses, we identified a set of typical roles that experiments play in mathematical practice, with special focus on the role as epistemic warrants.

1.2 What we expected to find

We intended the investigation to be exploratory and sat out with a fairly open mind. However, based on prior research, contemporary literature in philosophy of mathematical practice, discussions with mathematicians, and anecdotal evidence we also had some expectation about the roles experiments play in mathematics. We used these expectations to inform the focus and empirical design of the investigation in an iterative way. Especially, at several points in the investigation we compared early empirical results with our prior expectation and used this combination to point out new venues of further investigation. Thus, we were expecting to find traces of exploratory uses of experiments in practices concerning formulation and proof of mathematical hypotheses. We were expecting to find experiments given to illustrate mathematical claims and to suggest further directions of research, and (depending on the corpus) we further expected to find a large body of mentions of experiments in connections with collaborations between mathematics and empirical sciences.

The first step in the process was therefore to map the extent to which experiments were a topic of interest in the reviews that we study. Based on our prior assumptions, we expected to find reference to experiments on mathematical objects in statistics or connected to methods in fields such as number theory. And being focused on the role of experiments in mathematics, we also expected to find references to experiments in contexts that also involved computers.

Yet, when we began the quantitative analyses, we were surprised to see how frequent reference to experiments were in the reviews given that they were considered “back-stage” in the suggestive distinction of Hersh (1991), and that experiments mainly occurred in other fields than those typically studied as part of experimental mathematics. Thus, the first part of the analysis was to sample and code references to experiments, and in particular to their roles as epistemic warrants.

This first qualitative analysis provided us with a code book and a classification of experiments in nine different and distinct roles. This classification should be seen as one of the major contributions of this article. Yet, the classification showed that one of our prior assumptions was under-represented whereas we were surprised by another category: Given the experimental methodology adapted by experimental mathematics, we had expected to find some instances of experiments acting as strong epistemic warrants of either mathematical results or statements; yet, such instances were quite rare. On the other hand, from a purely formalist perspective, we were surprised by reviewers expressing that they lacked experiments in a publication. Thus, we decided to expand our methods and look closer into these two topics.

First, we sampled reviews specifically from the fields most prevalent in experimental mathematics and found that, indeed, reference to experiments as warrants were different in this corpus. Second, we directed our search to instances were reviewers expressed that they would have found experiments useful. We found a sufficient number of such instances that we could use these to also describe how such (missing) experiments would have played an epistemic role.

1.3 Structure of this paper

In Sect. 2, we describe the construction and processing of the Base Corpus, and the samples which we used for our qualitative analyses. This section also contains some quantitative qualification of the corpus. Then, in the central Sect. 3, we describe the qualitative analyses leading to a code book for classifying experiments in mathematical practice. In the process we provide prototypes from the reviews for most categories.

In Sect. 4, we challenge our original sample and code book by focusing on another sample drawn from fields more likely to contain experiments in the sense of experimental mathematics. This section both validates the code book and provide more instances where experiments were used as strong epistemic warrants.

In Sect. 5, we then ‘thicken’ the category in our code book covering expressions of lacking experiments. By ‘thickening’ a category, we mean efforts to deliberately search for similar instances based on characteristics extracted from the known exemplars, be it through keywords or metadata. Here, we use direct sampling to produce a sufficient number of instances to substantiate the existence of this category and to tie it to ideas about the epistemic warrants of experiments.

Finally, in Sect. 6, we summarize and discuss our findings. We argue that (1) experiments are more prevalent in mathematical practice than previously acknowledged; (2) experiments play different epistemic roles across different mathematical fields; and (3) our method of combining corpus studies and qualitative analyses has proved successful in addressing a part of mathematical practice otherwise difficult to access.

2 Preparing the corpus

2.1 The pipeline for MR data

The MR database contains bibliographic information of all mathematical papers published in the extensive list of journals and book series covered. Each record in the database contains information about the authors, title, year, publication venue etc. of the publication under review as well as a review. The review is written by a peer invited by the MR editorial team and is typically around 13.1 sentences (247 words) long.¹ In some cases, this post-publication peer review is replaced with the authors’ summary from the publication at hand. Importantly, the MR also contains a unique identifier for each publication (MR number) and information about its subject classification, referring to the Mathematical Subject Classification (MSC code) current at the time of publication.² Each MSC code contains a major field code and a specialization, and papers are allowed more than one code with the first one being the most important classification.

In the absence of a public API (application programming interface), the web interface of MR allows us to run simple queries on the database.³ It is possible to search for occurrences of strings in the various bibliographic elements, and to limit queries to particular subjects, time periods, or publication types. The results from such queries were returned in such a structured format, that automatic processing was possible. We used this query system for two purposes: To extract raw numbers of publications meeting certain criteria and to access metadata and reviews for the publications we sampled.

2.2 Filtering on primary MSC code

An initial query showed that the term “experiment” (and derivatives such as “experiments” and “experimental”) occurred in reviews of 94,732 publications recorded in the MR.⁴ This set of all records in MR in which the indicator term “experiment” occurs in the review field constitutes our Base Corpus. Since the sheer size of the Base Corpus prevented download and qualitative analyses, we needed some sampling to obtain manageable corpora. And as a way of splitting the data, we decided to look at the major, primary subject classification (abbreviated MPSC) of the publication, i.e. the first two digits in the first MSC code. Other restrictions to specific periods or correlations with occurrences of other indicator words such as “computer” were also considered, but although those seemed relevant to our a priori assumptions, they essentially appeared to preempt some of the interesting macro-level facts that we quickly found from focusing on the MSC class.⁵

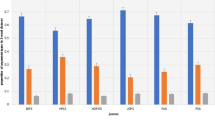
An analysis of the MPSC codes used in Base Corpus showed that 16 of the codes each accounted for more than 1% of the reviews. When combined, these 16 MPSC codes accounted for 86.5% of all reviews in Base Corpus (see Fig. 1).

Fig. 1

Percentage of reviews from Base Corpus (reviews containing the indicator word “experiment”), split by major, primary subject classification (MPSC) codes as listed in Mathematical Reviews (MR) and zbMATH (2020). An asterisk indicates that the MPSC code was included in Sample 1

2.3 Sampling from Base Corpus

For this project, we extracted three different samples from the Base Corpus (see Fig. 2). Each sample was set up to meet some general and some specific filtration criteria. The general criteria were that the review should come from Base Corpus and (for samples 2 and 3) that a reviewer should be identified in the record to avoid authors’ summaries.

The purpose of Sample 1 was to extract a broad body of reviews from MR referring to mathematics-centred experimental practices. For this purpose we took departure in the 16 MPSC codes identified above. The coverage of the MR, however, spans many disciplines on the intersection of mathematics and the natural sciences, so in order to further focus the sample, we decided to include only MPSC codes that were sure to give mathematics-centred uses of the indicator word and exclude codes where the field suggested a non-mathematics-centred experimental practice. This process narrowed the focus to the 6 MPSC codes marked with an asterisk in Fig. 1 and listed in Table 1, accounting for 47% of Base Corpus, and Sample 1 was constructed by randomly selecting 250 reviews from this sub-set of the Base Corpus. The selection was performed such that the marginal distribution of Sample 1 follows that of the Base Corpus restricted to the 6 specific MPSC codes.

The reviews in this sample were collected, processed using a LaTeX pipeline highlighting the indicator terms, and exported as PDF for coding.⁶ For a description of the coding and analysis of Sample 1, please refer to Sect. 3, below.⁷

Table 1 MPSC codes used in Sample 1 and Sample 2

Based on the coding of Sample 1 we noticed the almost complete lack of epistemic warrants in the form that we had expected based on a priori assumptions drawn mainly from the field of experimental mathematics. The purpose of Sample 2 was therefore twofold: First to solidify the code book developed for coding Sample 1, and second to extend the corpus into fields of mathematics where we would expect to find stronger epistemic warrants. For those purposes, we chose 3 new MPSC codes (see Table 1) in fields where we knew that leading proponents of experimental mathematics such as Jon Borwein had worked.

For a description of the coding and analysis of Sample 2, please refer to Sect. 4, below.

Among the interesting categories that emerged from coding Sample 1, we chose to focus on the reviewers’ expressions of missing an experiment in a publication. To get more instances of such expressions (and thus to thicken this category), we focused on the other words in sentences including the indicator word “experiment”. Based on an example, we had found in Sample 1 and our intuitions, we devised a set of additional indicator words (see Table 2) and used these to generate Sample 3.

Table 2 Additional indicator words signalling perceived lack of experiments, used in forming Sample 3

Sample 3 contains 417 sentences which were exported to a spreadsheet along with information on which qualifying indicator word (Table 2) that had been matched (for coding and results, see Sect. 5, below).

Fig. 2

Overview of the corpus and the three samples. Sample 1: From the reviews in Base Corpus with MPSC code among those 6 codes listed in Table 1, we randomly extracted 250 reviews which we refer to as Sample 1. Sample 2: From the reviews in Base Corpus with MPSC code listed in Table 1 and for which a reference to the journal Experimental Mathematics was not the only occurrence of the indicator word, we built Sample 2 by combining random samples of 50 reviews from each of the three MPSC codes. Sample 3: From the Base Corpus, we randomly sampled 1000 new records (i.e. records not already in Sample 1 or Sample 2). Each review was split into sentences, and if a sentence containing the experiment indicator also included one of the additional indicator words from Table 2, that sentence was included in Sample 3. MR numbers of all reviews included in the three samples can be found at https://doi.org/10.17894/ucph.c39d1ae1-e3df-4631-9dc8-9e175bb9c19d

3 Coding and classifying the roles of experiments

All 250 reviews from Sample 1 were coded in NVivo. The coding focused on the sentence or sentences including the indicator word “experiment” (or derivatives thereof), but when necessary other parts of a review were also included for context. The reviews were coded using a grounded approach (Charmaz, 2006) where the codes were developed as a response to the patterns and structures that emerged in the data, although we also allowed our theoretical understanding and expectations (see Sect. 1.2) to influence the process.

Codes were developed in an iterative process where the second author of the paper developed a first version of the code book and applied it to the full data set. The code book and examples of coding were then discussed in the author group. The epistemic role played by experiments and the fact that the reviewers would sometimes ask for more experiments were especially surprising results of the initial coding. Based on these results and our discussion of them the third author of the paper revised the code book through a grounded approach to allow more detailed analysis of these aspects of experiments, and re-coded the full data set (of Sample 1). This division of labor between the second and the third author of the paper was in part made for pragmatic reasons. The code book can be accessed at: https://doi.org/10.17894/ucph.c39d1ae1-e3df-4631-9dc8-9e175bb9c19d

In the final code book we operated with two top-level themes. The first regarded the object of the experiment and the second the role experiments played in the mathematical texts. Under each theme various sub-codes were developed and used.

The purpose of the first theme was simply to establish whether the experiments referred to in a given review were performed on mathematical or non-mathematical objects. To do so, all instances, understood as sentences including the term ‘experiment’, in the sample were coded with exactly one of the following three sub-codes:

• Mathematical object

• Not mathematical object

• Unable to discern

In a few cases the word “experiment” was used several times in the same sentence. If the two occurrences of the word referred to the same experiment in the same way, we would count them as one instance, and if not, we would count them as two instances.

The code Mathematical object was used when the experiment involved typical mathematical objects and processes such as (numerical) algorithms, functions, geometrical objects etc. A prototypical example would be:

In an experimental evaluation, the performance of the method is compared to the performance of recently developed numerical techniques for the approximate determination of all roots of trigonometric polynomials. (Schweikard, 1992)

The code Not mathematical object was used for instances where the term ‘experiment’ clearly did not refer to mathematical objects. This would typically be instances referencing books or journals that had the term “experiment” in their name, references to experimental mathematics as a field or references to experiments in other sciences. An example of the latter could be:

The feasibility of the DNA algorithm has been successfully tested on a small circuit by actual biochemical experiments. (Ogihara & Ray, 1999)

Although prototypical examples of both mathematical and non-mathematical objects were identified in the data set we also encountered grey-zone situations. Especially, we considered algorithms (such as optimization algorithms) to be mathematical objects, and computer programs to be non-mathematical objects, but the distinction between these two types of objects was not always clear-cut.

In cases where we could not determine the status of the object either because it was in a grey-zone or because the review did not contain enough information to make an informed decision we used the code Unable to discern.

In Sample 1 a total 166 instances were coded as Mathematical object, 103 as Not mathematical objects and 17 as Unable to discern.

Instances coded as Not mathematical objects or Unable to discern were not coded further. All instances coded with Mathematical object were coded using a set of codes aimed at describing the various roles experiments played in the mathematical texts according to the reviews. The coding thus reflects our analysis of the reviews, and not an analysis of the actual texts under review.

During the coding process the system of codes described in Figure 3 was developed in an iterative way as described above. The code book and references to the samples can be found in the supplementary material.

Fig. 3

Overview of the system of codes developed to describe the roles of experiments in Sample 1. Apart from the codes shown in the overview the following two opt-out codes were also used: Other and Unable to determine role

3.1 Code system for experiments concerning mathematical objects

All the 166 instances coded as mathematical objects were coded with exactly one of the five top-level codes in Figure 3 or as Other or Unable to determine role. As no instances were coded as Other in the final round of coding, the five codes constitute a system of mutually disjunctive categories that cover all instances in the sample. Apart from the overall categorization provided by this system of codes, we further introduced the code Result indicates future experiment that was used in addition to the other overall codes. The distribution of instances among the codes in Sample 1 can be seen in Table 3.

Table 3 Distribution of instances among codes describing the overall roles played by experiments in Sample 1. Only instances coded as having mathematical objects are included ($n=166$)

In the following we will give a short description of the codes in the code system along with prototypical examples of instances falling under each code. The prototypical examples should not necessarily be seen as typical or common, but rather as examples that model the category by representing its central idea (Rosch, 1983).

Reference to established knowledge was used to code instances where the term ‘experiment’ occurred as part of a reference to generally established knowledge or previously performed experiments. A prototypical example would be a direct reference to the literature such as:

In previous literature, this model has been heuristically linked to an experiment , where the anti-derivative of the regression function is continuously observed under additive perturbation by a fractional Brownian motion (Sharia, 2014)

We did however also include more casual references to ‘well-known’ results (e.g. Basu, 1974), and instances where where the term “experiment” was used as part of an established nomenclature, such as references to “Chebyshev experiments” in Munk (1998), or the general reference to “the optimal design of experiments” (in what we judged to be a domain of mathematical objects) in Ramírez (2011). Sub-codes were introduced to point out instances with a specific reference to previously performed experiments, and instances where “experiment” was part of a general nomenclature.

The code Heuristics or exploration was used in cases where the experiment was judged to serve mainly a heuristic purpose or was part of an exploratory study. This function would typically be indicated by the use of terms such as “investigate”, “indicate”, “study”, “discuss”, “motivated by” or similar to describe the role played by experiments. A prototypical example could be:

Computational experiments indicate that the results can be useful for reducing the size of branch-and-bound trees. (Kaibel, 2006)

The code Epistemic warrant was used to code instances where the experiment had a clear epistemic function in the reviewed mathematical text, marked by the use of words such as “test”, “verify”, “demonstrate”, “confirm”, “compare”, “indicate”, “suggest” or similar. This category however was not heterogeneous and during the coding process two important dimensions in epistemic function emerged. The first concerned the object of the experiment and the second the strength of the epistemic warrant the experiment was supposed to give. To capture this diversity within the category we introduced two pairs of sub-codes.

With the first pair of codes we distinguished between cases where the experiment was presented as the primary or sole epistemic warrant and cases where it was given in combination with other warrants such as deductive or analytic considerations. The former was coded as Primary warrant and the latter as Mixed warrant, and all instances coded as Epistemic warrant were coded to exactly one of these two sub-categories.

With the second pair of sub-codes we distinguished between instances where the warrant concerned algorithms or methods and instances where it concerned theorems or statements in a more classical sense. All instances coded as Epistemic warrant were also coded to exactly one of these two sub-categories. So in sum, instances where experiments served as epistemic warrant were coded as belonging to one of four sub-categories depending on the type of warrant and the object of the claim warranted. An overview of the sub-categories and distribution of the instances among them can be seen in Table 4.

Table 4 Distribution of instances where experiments were used for epistemic warrant in Sample 1. Shares of total ($n=99$) are given in parentheses

A prototypical example of a Primary warrant concerning Algorithms or methods could be:

The proposed modification provides a closer approximation to the exact maximum likelihood estimators. Simulation experiments which demonstrate the effectiveness of this modification are presented. (McLeod, 1977)

A prototypical example of a Mixed warrant concerning Algorithms of methods could be:

The algorithm is shown to converge linearly under convexity assumptions. Both theory and numerical experiments suggest that it generally converges faster than the Polak-Trahan-Mayne method of centers. (Pillo, 1992)

As can be seen in Table 4, we only found two instances in Sample 1 where experiments served as epistemic warrant in connection to theorems or statements, and in both these cases they were used as a mixed warrant. In the first case, the review opens with an outline of a theoretical argument and ends with: “At last, some numerical experiments are presented to confirm the theoretical analysis” (Keinert, 2011). The second case has a similar structure, and ends with “This is confirmed by 1D and 2D numerical experiments” (Pultarová, 2011).

The code Proposed experiment was used in cases where the sole function of the term “experiment” in the review was to point out experiments that could or should have been made either according to the reviewer or the paper under review. The following instance can be seen as a prototypical case:

At the end there are concluding remarks that propose several methods for constructing 3-orthogonal column orthogonal designs for computer experiments. Ghosh (2014)

The sub-code Comment on lack of experiment was used to point out cases where the reviewer in our interpretation believed an experiment ought to have been made. The code was only used once in Sample 1 to code the instance:

The paper is rather focused on the theoretical analysis of the algorithm (no numerical experiments are presented) (Baeza, 2017).

In cases where some experiments had already been carried out, but further experiments were suggested, the instance would be classified with the code describing the existing experiments, and we would use Result indicates future experiment as an additional code. In Sample 1 this code was only used once in the following instance (also coded as mixed epistemic warrant for algorithm or method):

Algol programs implementing the new methods are given and a simple numerical experiment is described. Further numerical comparisons would seem likely to be worthwhile. Gladwell (1974)

Finally, the code Communication or pedagogy was used to code instances where experiments were described in epistemically neutral terms such as “included” or “presented”. Typically, such descriptions would come after the description of the main mathematical results. The following two instances can be seen as a prototypical examples:

Furthermore, we apply these techniques to obtain a fast wavelet decomposition algorithm on the sphere. We present the results of numerical experiments to illustrate the performance of the algorithms. Böhme and Potts (2003)

The discussion includes detailed calculation of quantities occurring in algorithms, proofs of convergence, discussion of errors and results of numerical experiments. Szeptycki (1988)

In some cases (such as the last of the two examples given above) it could not be ruled out that the experiments also played an epistemic role. However, in the absence of epistemic language or other clear indications of epistemic use we would always code the instance as Communication or pedagogy.

To summarize, the analysis of Sample 1 allowed us to develop a system of codes that reflects the main roles experiments played in the reviews included in the sample (Fig. 3). The results also clearly showed that experiments were used as epistemic warrants. In fact, the role as epistemic warrant was by far the most common (60%) in the sample, whereas experiments in much fewer of the instances were used for communication (15%) and heuristic or exploratory purposes (11%) (see Table 3).

It was also a surprise that experiments were in some cases proposed or demanded, although we only saw very few instances in this category.

4 Challenging the corpus: What about experimental mathematics?

To build on and expand the results presented above we extracted and examined two more samples from the Base Corpus. As described in Sect. 2, Sample 2 was drawn from journals where we expected the field of experimental mathematics to be strongly represented. The inclusion of this sample allowed us to challenge the system of codes developed directly to fit Sample 1 and to compare the epistemic roles of experiments in the specialized field of experimental mathematics with the areas included in Sample 1.

The 150 reviews in Sample 2 were coded by the third author of the paper using the procedure and code system developed in the coding of Sample 1, i.e. for each instance that included the indicator word “experiment” we would first determine if the object of the experiment was mathematical or not, and for instances where the object was mathematical we would code the role of the experiment using the system of codes described in the previous section (Fig. 3).

A total of 170 instances of the indicator word “experiment” were identified in Sample 2. Among these instances, 128 were coded as having a mathematical object. The distribution of these instances among the overall codes can be seen in Table 5.

Table 5 Distribution of instances among codes describing the overall roles played by experiments in Sample 2. Only instances coded as having mathematical objects are included ($n=128$)

The code Other was not used in any instances. The roles played by experiments in the two samples could thus be captured using the same system of codes. This shows that the system is robust in the sense that it could be applied outside the domain in which it was developed. Although other categorizations could possibly be developed, this indicates that the system of categories represented by our codes are likely to reflect the central roles experiments play in mathematics (at least in the fields covered by our Base Corpus).

If we compare the distribution of codes in Sample 1 (Table 3) and Sample 2 (Table 5) the role as epistemic warrant is clearly less frequent in Sample 2 (38%) than in Sample 1 (60%). Apart from that the overall profiles of the two distributions are similar in the sense that the ranking of the codes by shares is the same in the two samples, and that all of the codes except Epistemic warrant are represented with (roughly) comparable shares (differences ranging from 2 to 7 percentage points).

If we turn to the set of sub-codes describing the epistemic roles played by experiments we do however see clear differences between the two samples. The distribution of the sub-codes for Sample 2 are seen in Table 6. Whereas experiments were rarely used to warrant theorems or statements in Sample 1 (Table 4) the majority (52%) of instances in Sample 2 have exactly this function (Table 6). This marks a clear and important difference between the field of experimental mathematics (as represented by Sample 2) and the more general use of experiments (as represented by Sample 1).

Table 6 Distribution of instances where experiments were used for epistemic warrant in Sample 2. Shares of total ($n=48$) are given in parentheses

If we explore the cases in Sample 2 where experiments were used as primary warrants for theorems or statements it is worth noticing that although the warrant was considered to be weak in some instances (indicated by the use of words such as “suggest”), the warrant was just as often considered to be strong (indicated by terms such as “show” or even “demonstrate”). The following is an example of the first type (weak evidence):

The paper reports numerical experiments suggesting that for maps of this kind on [MATHINLINE] digit inputs (written in base [MATHINLINE]) “stochasticity” persists beyond the first [MATHINLINE] iterations. (Lagarias, 2002, The string “MATHINLINE” is inserted here to replace strings of mathematical symbols in the original text)

As an example of the second type (strong evidence) we can look at the following:

He relies on numerical experiments to demonstrate a remarkably regular structure of the complex roots of such polynomials. Doha (2012)

It is highly interesting that experiments are considered to constitute epistemic warrants of this strength even for theorems and statements.

If we turn to mixed warrants for theorems and statements the description of the experiments typically include terms such as “verify”, “show”, “confirm” or similar. The following can be seen as a prototypical example:

The conclusions are tested by numerical experiments and show that the derived bounds for the truncation errors of the addition theorems are valid. Segura (2016)

It should also be noted that in some of these instances the statement being warranted was refereed to as a “conjecture”, which indicates the combined evidence was not seen as complete.

5 Thickening the corpus: When are experiments wanted, but not provided?

When coding and analysing Sample 1, we found the sub-code Comment on lack of experiment particularly interesting, although only a single instance was identified. In the case in question it seemed that the reviewer wanted an experiment included which, however, was not found. We speculated that this might suggest that the reviewer felt an experiment would have strengthened the claims made in the publication under review.

Therefore, we wanted to thicken the category in the sense that we wanted to find additional instances falling under it through a targeted search process using specific search terms, as described above (Sect. 2.3). This procedure resulted in Sample 3 consisting of 417 sentences.

All 417 sentences were coded by the first author of the paper and in total 18 of them fell into the category Comment on lack of experiment. Each of these were picked out by one of the qualifying indicator words “no”, “not”, “would”, and “unfortunately” from Table 2.

Listing just three instances, we can begin to see, what experiments would have contributed to the publication under review:

The theoretical content of the paper appears interesting; it would be very desirable to see experimental results concerning its use. (Sage, 1976)

It would be quite interesting to see an analysis of the various constants involved, plus a detailed experimental validation. (Makris, 2007)

It would have been beneficial if this paper had also conducted numerical experiments to demonstrate the performance of this method, particularly the convergence rate of the method, its stability, and the scale of the algebraic systems that this method is most applicable for. (Lee, 2016)

As presented here, the three instances show different epistemic roles of the lacking experiments: Sometimes, experiments could have been included to bridge the divide between theory and use; in another instance, experiments could have provided validation; and in the final instance chosen, experiments would have been able to qualify the power, stability, and range of a presented method. The epistemic warrant that the missing experiments would have granted to the publication seems to be increasing over these three examples, from simply communicating the usefulness of a result to providing validation and qualification.

Thus, this exploratory thickening of the code Comment on lack of experiment supplement our analyses of the epistemic warrants that experiments can possibly provide. Comments on lack of experiments illustrate how peers and members of the intended readership could have found experiments useful for their understanding and trusting published results. And such comments are not that rare in the Base Corpus considered here; and, as shown, they refer to providing information and validation of algorithms and methods applied within mathematics.

As we coded the 417 sentences in Sample 3 it became clear that reviewers would comment on the use of experiments in interesting ways not covered by the code Comment on lack of experiment. Especially, we encountered a few instances where the reviewer found an experiment that had been performed inadequate. This could either be because the experiment itself was seen as insufficient (16 instances) or because the documentation was lacking (4 instances).

6 Discussion

Our method of combining sampling from the corpus of reviews in MR with qualitative analyses has proven successful insofar as it has given us access to philosophical analyses of a part of mathematical practice that is otherwise difficult to access. In mathematical research practice, the publication of a result after peer review is only one step towards the broader acceptance of the result into the edifice of mathematical knowledge. Empirically studying processes of post-publication peer review allowed us to gauge the roles of certain epistemic practices, such as the use of experiments in contemporary mathematical research, and provide us with an angle on the normative functions that corpora such as MR impose.

Using a combination of random and directed sampling from a corpus of reviews in the Mathematical Reviews, we have been able to conduct qualitative analyses of the ways experiments enter into the processes of post-publication assessment of mathematical works.

From a broad sample of reviews from those mathematical fields most likely to contain experiments with mathematical objects, we concluded that experiments are particularly prevalent in reviews of works in fields of statistics, numerical analyses, computer science, operations research, and systems theory. We also found a substantial number of references to experiments in partial differential equations. Thus, these six fields became the basis for our qualitative classification of the roles of experiments and the development of our code book.

This code book contained a variety of different roles of experiments that could perhaps be seen as placed on a spectrum from indirect epistemic impact in referring to established knowledge, over serving as heuristics or exploration to explicitly serving as epistemic warrants, either of theorems or of methods, and either alone or in combination with other warrants. To these categories, we also added situations where experiments actually did not provide epistemic warrant, either because they were lacking or because they were discussed in a context of communication or pedagogy. For the broad sample of six fields, we found that the majority of experiments served as mixed warrants for algorithms or methods.

The fact that most of the fields included in the broad sample could be seen to be non-pure mathematical disciplines (as illustrated by their high major, primary subject classification) and that we found very few experiments serving as epistemic warrants for theorems and statements led us to challenge our sample. We picked out three mathematical fields in which main protagonists of experimental mathematics had published and sampled reviews from these. The qualitative classification of this sample showed that the code book previously developed was robust enough to include these different domains and that, indeed, fields such as number theory, combinatorics, and special functions did refer to experiments as epistemic warrants for theorems. This result shows that the use of experiments in mathematical practice challenges traditional, formalist conceptions of mathematical epistemology.

When we also saw that lack of experiments were sometimes commented upon by reviewers, we directed our search to find more instances of this kind. What we found was that indeed, the category could be thickened. When we did so, we found sufficiently many instances to allow us to suggest that a reviewer could bemoan a lack of experiment since it could have tied theory and use together, or it could have provided validation, or it could have served as qualification for results. These are thus also epistemic roles that experiments can play.

These findings point to more general conclusions that can be drawn from our investigation which add to the existing philosophical work on the role experiments play in establishing conviction in mathematics.

The empirical fact that experiments do exist in mathematical publications and are sometimes desired by reviewers should establish that experiments do play a role in mathematical practice. In some fields (mainly physical and computational sciences) that role may be to corroborate material experiments or estimate run-times for algorithms, but in other fields other types of warrant are provided by experiments. There, experiments may serve as motivation or as secondary or primary warrant for mathematical claims, in some cases even claims concerning theorems and statements. Thereby this study also shows that mathematical practice varies between fields as pertains to the role of experiments.

Any empirical study is prone to limitations. First, we could always want a larger corpus, but our experience was that the coding scheme was well saturated at the sample sizes that we chose. A more serious limitation is that this study and its corpus consists of post-publication reviews which, obviously, are biased by the single author of the review into what is important. Nevertheless, we suggest that even a single angle, when explored from a large corpus, on an otherwise hidden aspect of mathematical practice is fruitful—other approaches using other corpora are, of course, also possible (for one such approach, see also Sørensen, 2024). Yet, to some extent, our corpus propagates a certain selection bias from the MathSciNet. The best way to mitigate such limitations is to seek triangulation.

Adding to other empirical work which has established that mathematicians rely on a variety of non-formal factors (including experiments) in obtaining conviction about theorems and proofs (see e.g. Weber et al., 2014), our analyses of the roles of experiments point to two new functions of this part of mathematical practice.

First, we suggest that experiments may provide ‘dual warrants’ of statements, very much in line with the program of experimental mathematics. In that program, statements and experiments are intertwined in the epistemic process such that experiments may be required or wanted both to illustrate essential ideas or concepts and to provide pathways to a proof (see e.g. Sørensen, 2010). Our approach of selecting mathematical fields that are prone to experimental practices has been supported by other empirical studies of experimental mathematics: Indeed, number theory and combinatorics are the top disciplines pursued by the culture of experimental mathematics (Sørensen, 2024).

Second, we see that experiments can serve to triangulate mathematical statements about certain mathematical objects in the sense that they can be used to warrant a statement in combination with other means of warranting. This contribute to the robustness of mathematical knowledge by adding connections in the graph of mathematical results (see e.g. Faris and Maier (1991) and Viteri and DeDeo (2022)) This picture of mathematical practice contrasts a more traditional epistemology, where rigid deductions and formal proofs are seen as the primary (or only) way of warranting a mathematical statement (see e.g. Azzouni (2004)). This traditional epistemology leaves little room for experiments as epistemic warrants, as experiments and other forms of empirical generalization cannot deliver the kind of certainty aimed at in the traditional epistemology. The investigation of the roles experiments play in mathematical practice shows that mathematicians do not always share the traditional idea that only rigid deductions can carry epistemic weight in mathematics. Thus, this combined quantitative and qualitative study and philosophical reflection triangulate mathematical practice to show that experiments are much more prevalent and much more important in mathematical practice than a traditional epistemology of mathematics would have us believe.